目录
前言
本文其实值属于:程序员的数学【AIoT阶段二】 (尚未更新)的一部分内容,本篇把这部分内容单独截取出来,方便大家的观看,本文介绍 线性代数高级,读之前建议先看:程序员的数学【线性代数基础】,本文涵盖了一些计算的问题并使用代码进行了实现,安装代码运行环境见博客:最详细的Anaconda Installers 的安装【numpy,jupyter】(图+文),如果你只是想要简单的了解有关线代的内容,那么只需要学习一下博文:NumPy从入门到高级,如果你是跟着博主学习
A
I
o
T
AIoT
AIoT 的小伙伴,建议先看博文:数据分析三剑客【AIoT阶段一(下)】(十万字博文 保姆级讲解),如果你没有
P
y
t
h
o
n
Python
Python 基础,那么还需先修博文:Python的进阶之道【AIoT阶段一(上)】(十五万字博文 保姆级讲解)
一、特征值和特征向量
1.1 概念定义
🚩两个向量相乘效果图如下:
看图,这张图片竖直方向进行偏移,形象说明了向量相乘效果:
设
A
A
A 是
n
n
n` 阶方阵,如果存在数
λ
\lambda
λ 和非零
n
n
n 维列向量
v
v
v,使得
A
v
⃗
=
λ
v
⃗
A\vec{v} = \lambda\vec{v}
Av=λv 成立,则称
λ
\lambda
λ 是矩阵
A
A
A 的一个特征值(eigenvalue),
v
⃗
\vec{v}
v 是特征值
λ
\lambda
λ 对应的特征向量(eigenvector) 。

矩阵
A
A
A 对向量
v
⃗
\vec{v}
v 进行变换,这个变换的特殊之处是当它作用在特征向量
v
⃗
\vec{v}
v 上的时候,
v
⃗
\vec{v}
v 只发生了缩放变换,它的方向并没有改变,并没有旋转。
观察发现,
v
⃗
\vec{v}
v 和
A
v
⃗
A\vec{v}
Av 在同一条直线上,只是长度不同,此时我们称
v
⃗
\vec{v}
v 是
A
A
A 的特征向量,而
A
v
⃗
A\vec{v}
Av 的长度是
v
⃗
\vec{v}
v 长度的
λ
\lambda
λ 倍,
λ
\lambda
λ 就是特征值。
如果
n
n
n 阶方阵
A
A
A 是满秩矩阵,那么矩阵
A
A
A 有
n
n
n 个不同的特征值和特征向量。
import numpy as np
A = np.random.randint(1,10, size =(4,4))
display(A)print('------------------------')if np.linalg.matrix_rank(A)==4:# 必须是满秩矩阵# 实对称矩阵特征值为实数,非对称矩阵和复矩阵特征值可能为复数
w, v = np.linalg.eig(A)# 返回特征值和特征向量
display(w, v)
w = np.real(w)
v = np.real(v)print('------------------------')
display(A.dot(v[:,0]))
display(w[0]* v[:,0])

实对称矩阵,求解特征值和特征向量为实数
# 实对称矩阵import numpy as np
B = np.array([[1,2,3],[2,5,8],[3,8,9]])
np.linalg.eig(B)

矩阵的秩: 用初等行变换将矩阵
A
A
A 化为阶梯形矩阵, 则矩阵中非零行的个数就定义为这个矩阵的秩, 记为
r
(
A
)
r(A)
r(A)。


经过初等变换可知这个方程无解。
import numpy as np
X = np.array([[1,2,3],[4,5,6],[7,8,2]])
y = np.array([1,2,3])# 查看矩阵秩,输出结果为2print('矩阵X的秩为:',np.linalg.matrix_rank(X))# 尝试求解报错,说明方程没有唯一解
np.linalg.solve(X,y)

1.2 满秩矩阵
🚩满秩矩阵(non-singular matrix): 设
A
A
A 是
n
n
n 阶矩阵, 若
r
(
A
)
=
n
r(A)=n
r(A)=n, 则称
A
A
A 为 **满秩矩阵**。但满秩不局限于
n
n
n 阶矩阵。若矩阵秩等于行数,称为行满秩;若矩阵秩等于列数,称为列满秩。既是行满秩又是列满秩则为
n
n
n 阶矩阵即 **
n
n
n 阶方阵**。


根据初等行变换,可得:
x
1
=
−
2
3
≈
−
0.67
x_1=-\frac{2}{3}≈-0.67
x1=−32≈−0.67
x
2
=
−
5
3
≈
1.67
x_2=-\frac{5}{3}≈1.67
x2=−35≈1.67
x
3
=
−
7
3
≈
2.33
x_3=-\frac{7}{3}≈2.33
x3=−37≈2.33
1.3 方程的解
import numpy as np
X = np.array([[0,2,-1],[1,-1,1],[2,1,-1]])
y = np.array([1,0,-2])# 查看矩阵秩print('矩阵X的秩为:',np.linalg.matrix_rank(X))# 尝试求解报错,说明方程没有唯一解
np.linalg.solve(X,y).round(2)

1.4 特征值和特征向量示例
🚩所有特征值的乘积等于
A
A
A 的行列式的:
∏
i
=
1
n
λ
i
=
∣
A
∣
\prod\limits_{i=1}^{n}\lambda_i=|A|
i=1∏nλi=∣A∣
import numpy as np
X = np.array([[2,3,7],[1,5,8],[0,4,9]])# w表示特征值,v表示特征向量
w,v = np.linalg.eig(X)print('矩阵X的行列式:',np.linalg.det(X))print('特征值累乘值:',np.round(np.real(np.prod(w))))

特征值和特征向量在机器学习中会被用到,像
P
C
A
PCA
PCA 主成分分析,
L
D
A
LDA
LDA 线性判别分析,以及其它算法里面都会用到它的理论和方法。
二、特征值分解
2.1 特征值分解定义与操作
🚩特征值分解,就是将矩阵
A
A
A 分解为如下式:
A
=
Q
∑
Q
−
1
A=Q\sum Q^{-1}
A=Q∑Q−1
其中,
Q
Q
Q 是矩阵
A
A
A 的**特征向量**组成的矩阵,
∑
\sum
∑ 则是一个**对角阵**,对角线上的元素就是**特征值**。
∑
=
[
λ
1
λ
2
⋱
λ
n
]
\sum=\left[ \begin{matrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \\ \end{matrix} \right]
∑=⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤
import numpy as np
A = np.array([[7,8,4,3],[2,9,6,8],[1,6,9,6],[7,9,7,3]])# w(Σ)表示特征值,v(Q)表示特征向量
w, v = np.linalg.eig(A)print('矩阵A的特征值和特征向量:')
display(w, v)# 根据特征值分解公式可得print('特征值和特征向量运算反推矩阵A:')
display(v.dot(np.diag(w)).dot(np.linalg.inv(v)))

如果矩阵
A
A
A 是对称矩阵,那么
Q
Q
Q 是正交矩阵,正交矩阵的定义是
Q
Q
Q 的逆等于
Q
Q
Q 的转置
Q
−
1
=
Q
T
Q^{-1}=Q^T
Q−1=QT
# 实对称矩阵import numpy as np
B = np.array([[1,2,3],[2,5,8],[3,8,9]])# w(Σ)表示特征值,v(Q)表示特征向量
w,v = np.linalg.eig(B)print('矩阵A的特征值和特征向量:')
display(w, v)print('特征值和特征向量运算反推矩阵A:')
display(v.dot(np.diag(w)).dot(np.linalg.inv(v)))
display(v.dot(np.diag(w)).dot(v.T))print('Q是正交矩阵:')
display(np.linalg.inv(v), v.T)

2.2 特征值分解意义
🚩一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。
当矩阵是高维的情况下,那么这个矩阵就是高维空间下的一个线性变换,这个线性变化可能没法通过图片来表示,但是可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前 N 大特征向量,那么就对应了这个矩阵最主要的 N 个变化方向。我们利用这前 N 个变化方向,就可以近似表达这个矩阵(变换)。也就是说的:提取这个矩阵最重要的特征。
总结一下,特征值分解可以得到特征值与特征向量,特征值大小表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。
不过,特征值分解也有很多的限制,比如说变换的矩阵必须是方阵。
三、矩阵和向量求导公式
3.1 常见矩阵求导公式
🚩有六种矩阵求导公式如下:
3.2 向量求导公式
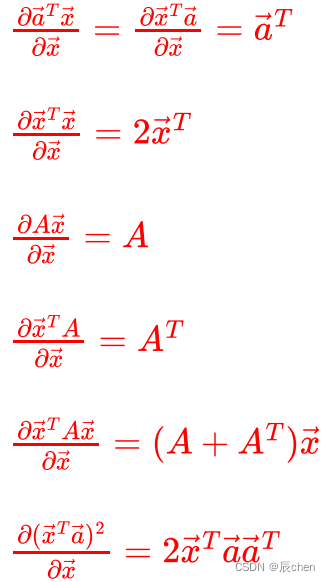
3.3 矩阵求导公式

转置公式如下:
( m A ) T = m A T (mA)^T=mA^T (mA)T=mAT,其中 m m m 是常数( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT( A T ) T = A (A^T)^T=A (AT)T=A
四、奇异值分解(SVD)
4.1 什么是奇异值分解
🚩特征值分解是一个提取矩阵特征很不错的方法,但是它只适用于方阵。而在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有
m
m
m 个学生,每个学生有
n
n
n 科成绩,这样形成的一个
m
∗
n
m * n
m∗n 的矩阵就可能不是方阵,我们怎样才能像描述特征值一样描述这样一般矩阵呢的重要特征呢?奇异值分解就是用来干这个事的,奇异值分解是一个能适用于任意的矩阵的一种分解的方法。
A
=
U
∑
V
T
A=U\sum V^T
A=U∑VT
假设
A
A
A 是一个
m
∗
n
m * n
m∗n 的矩阵,那么得到的
U
U
U 是一个
m
∗
m
m * m
m∗m 的方阵(里面的向量是正交的,
U
U
U 里面的向量称为**左奇异向量**),
∑
\sum
∑ 是一个
m
∗
n
m * n
m∗n 的实数对角矩阵(对角线以外的元素都是
0
0
0,对角线上的元素称为**奇异值**),
V
T
V^T
VT 是一个
n
∗
n
n * n
n∗n 的矩阵,里面的向量也是正交的, 里面的向量称为**右奇异向量**),从下图片来反映几个相乘的矩阵的大小关系:

4.2 奇异值与特征值关系
🚩特征值分解:
A
=
Q
∑
Q
−
1
A=Q\sum Q^{-1}
A=Q∑Q−1
奇异值分解:
A
=
U
∑
V
T
A=U\sum V^T
A=U∑VT
那么奇异值和特征值是怎么对应起来的呢?首先,我们将矩阵
A
A
A 的转置 和
A
A
A 做矩阵乘法,将会得到一个方阵,我们用这个方阵求特征值可以得到:
(
A
T
A
)
v
i
⃗
=
λ
i
v
i
⃗
(A^TA)\vec{v_i}=\lambda_i\vec{v_i}
(ATA)vi=λivi
这里得到的
v
i
⃗
\vec{v_i}
vi,就是我们上面的**右奇异向量**。然后,我们将矩阵
A
A
A 和
A
A
A 的转置做矩阵乘法,将会得到一个方阵,我们用这个方阵求特征值可以得到:
(
A
T
A
T
)
u
i
⃗
=
λ
i
u
i
⃗
(ATA^T)\vec{u_i}=\lambda_i\vec{u_i}
(ATAT)ui=λiui
这里得到的
u
i
⃗
\vec{u_i}
ui,就是我们上面的**左奇异向量**。
此外我们还可以得到:
A
=
U
∑
V
T
A=U\sum V^T
A=U∑VT
A
V
=
U
∑
V
T
V
AV=U\sum V^TV
AV=U∑VTV
因为
A
T
A
A^TA
ATA,
A
A
T
AA^T
AAT 是对称矩阵,所以
V
,
U
V,U
V,U 是正交矩阵,正交矩阵的定义是
V
V
V 的逆等于
V
V
V 的转置,即
V
T
V
=
V
−
1
V
=
I
,
U
T
U
=
U
−
1
U
=
I
V^TV=V^{-1}V=I,U^TU=U^{-1}U=I
VTV=V−1V=I,UTU=U−1U=I
A
V
=
U
∑
AV=U\sum
AV=U∑
A
v
i
⃗
=
σ
i
u
i
⃗
A\vec{v_i}=\sigma_i\vec{u_i}
Avi=σiui
σ
i
=
∣
A
v
i
⃗
∣
u
i
⃗
\sigma_i=\frac{|A\vec{v_i}|}{\vec{u_i}}
σi=ui∣Avi∣
这里的
σ
i
\sigma_i
σi 就是上面说的**奇异值**。
对
A
A
T
AA^T
AAT 以及
A
T
A
A^TA
ATA 做特征值分解,即可得到奇异值分解的结果。但是样分开求存在一定的问题,由于做特征值分解的时候,特征向量的正负号并不影响结果,比如:

如果在计算过程取,取上述的
u
i
⃗
\vec{u_i}
ui 组成的左奇异矩阵
U
U
U,取
−
v
i
⃗
-\vec{v_i}
−vi 组成右奇异矩阵
V
V
V,此时
A
≠
U
∑
V
T
A≠U\sum V^T
A=U∑VT。因此在求
v
i
⃗
\vec{v_i}
vi 时,要根据
u
i
⃗
\vec{u_i}
ui 来求,这样才能保证
A
=
U
∑
V
T
A=U\sum V^T
A=U∑VT。
解决方案:
1.计算特征值:
A
=
U
∑
V
T
A=U\sum V^T
A=U∑VT
A
A
T
=
U
∑
V
T
V
∑
T
U
T
=
U
∑
∑
T
U
T
AA^T=U\sum V^TV\sum^TU^T=U\sum \sum^TU^T
AAT=U∑VTV∑TUT=U∑∑TUT,根据结合律
V
T
V
=
I
V^TV=I
VTV=I,因此可化简:得到左奇异矩阵
U
∈
R
m
×
m
U∈R^{m\times m}
U∈Rm×m,根据上面分解公式可知,奇异矩阵为特征值开平方。
2.间接求右奇异矩阵:求
V
∈
R
m
×
m
V ∈ R^{m\times m}
V∈Rm×m
因为:
A
=
U
∑
V
A=U\sum V
A=U∑V
所以:
(
U
∑
)
−
1
A
=
(
U
∑
)
−
1
U
∑
V
(U\sum)^{-1}A=(U\sum)^{-1}U\sum V
(U∑)−1A=(U∑)−1U∑V
V
=
(
U
∑
)
−
1
A
V=(U\sum)^{-1}A
V=(U∑)−1A
V
=
∑
−
1
U
−
1
A
V=\sum^{-1}U^{-1}A
V=∑−1U−1A
V
=
∑
−
1
U
T
A
V=\sum^{-1}U^TA
V=∑−1UTA,因为
U
U
U 是正交矩阵,所以
U
−
1
=
U
T
U^{-1}=U^T
U−1=UT
五、求解奇异值分解
5.1 方式一
🚩根据上面对应公式,进行奇异值分解:
import numpy as np
A = np.array([[3,4,5,5],[7,5,3,6],[6,5,7,7],[4,9,8,9],[5,10,5,7]])# 左奇异矩阵
sigma,U = np.linalg.eig(A.dot(A.T))# 降序排列后,逆序输出
index = np.argsort(sigma)[::-1]# 将特征值对应的特征向量也对应排好序
sigma = sigma[index]
U = U[:, index]print('左奇异矩阵如下:')
display(U)# 计算奇异值矩阵
sigma = np.sqrt([s if s >0else0for s in sigma])print('奇异值为:')
display(sigma[:4])# 计算右奇异矩阵# 奇异值矩阵特殊,斜对角线有值,其余都是0# 奇异值矩阵的逆矩阵
sigma_inv = np.diag([1/ s if s >0else0for s in sigma])
V = sigma_inv.dot((U.T).dot(A))print('右奇异矩阵如下:')
display(V[:4])print('使用奇异值分解还原矩阵A:')
U.dot(np.diag(sigma)).dot(V).round(0)

5.2 方式二
🚩根据,
N
u
m
P
y
NumPy
NumPy 提供的方法,进行奇异值求解
import numpy as np
A = np.array([[3,4,5,5],[7,5,3,6],[6,5,7,7],[4,9,8,9],[5,10,5,7]])
u, s, v =np.linalg.svd(A)# 奇异值分解
display(u, s, v)

六、奇异值分解性质
🚩奇异值
σ
i
\sigma_i
σi 跟特征值类似,在矩阵
∑
\sum
∑ 中也是从大到小排列,而且
σ
\sigma
σ 的减小特别的快,在很多情况下,前
10
%
10\%
10%甚至
1
%
1\%
1% 的奇异值的和就占了全部的奇异值之和的
99
%
99\%
99% 以上了。也就是说,我们也可以用前
r
r
r 大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
A
m
×
n
≈
U
m
×
r
∑
r
×
r
V
r
×
n
T
A_{m\times n} ≈ U_{m \times r}\sum_{r \times r}V^T_{r\times n}
Am×n≈Um×r∑r×rVr×nT
r
r
r 是一个远小于
m
m
m、
n
n
n 的数。这样的矩阵乘法表示如下:

右边的三个矩阵相乘的结果将会是一个接近于
A
A
A 的矩阵,在这儿,
r
r
r 越接近于
n
n
n,则相乘的结果越接近于
A
A
A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵
A
A
A,我们如果想要**压缩**空间来表示原矩阵
A
A
A,我们存下这里的三个矩阵:
U
U
U、
Σ
Σ
Σ、
V
V
V就好了。
说句大白话,称作「奇异值」可能无法顾名思义迅速理解其本质,那咱们换个说法,称作「主特征值」,你可能就迅速了然了。
对于非奇异(满秩)矩阵,对应着特征值;对于奇异矩阵,就需要进行奇异值分解,对应着奇异值。对于奇异矩阵,将
A
A
A 与其转置相乘
A
T
A
A^TA
ATA 将会得到一个方阵,再求特征值。值得注意的是,对于非奇异矩阵进行奇异值分解(
S
V
D
SVD
SVD),得到的奇异值,其实就是特征值。
import numpy as np
A = np.array([[3,4,5,5],[7,5,3,6],[6,5,7,7],[4,9,8,9],[5,10,5,7]])
u, s, v =np.linalg.svd(A)
m, n = A.shape
Σ = np.concatenate([np.diag(s), np.full(shape =(m - n,n), fill_value =0)])print('通过奇异值分解还原原数据:')
display(u.dot(Σ).dot(v))# 抽取一部分奇异值,近似表示print('用前r大的奇异值来近似描述矩阵:')
r =2
display(u[:,:r].dot(Σ[:r,:r]).dot(v[:r]).round(1))

七、SVD进行数据压缩
🚩根据奇异值分解,进行数据压缩,以图片为例进行展示:
首先我们需要下载一张图片:
链接:https://pan.baidu.com/s/1pyywQWO4U4WWxtuAhAQHMQ?pwd=l7vv
提取码:l7vv
import numpy as np
import matplotlib.pyplot as plt
# 图片压缩defpic_compress(r, img):
u, sigma, vt = np.linalg.svd(img)
compress_img = np.dot(np.dot(u[:,:r], np.diag(sigma[:r])), vt[:r,:])# 还原图像
size = u.shape[0]* r + r * r + r * vt.shape[1]# 压缩后大小return compress_img, size
filename ='./bird.jpg'
img = plt.imread(filename)[:,:,0]# 取其中的一个颜色通道
compress_img, size = pic_compress(30, img)print('原图尺寸:'+str(img.shape[0]* img.shape[1]))print('压缩尺寸:'+str(size))# 图片绘制
fig, ax = plt.subplots(1,2,figsize =(12,4))
ax[0].imshow(img,cmap ='gray')
ax[0].set_title('before compress')
ax[1].imshow(compress_img,cmap ='gray')
ax[1].set_title('after compress')
plt.show()

八、SVD进行PCA降维
import numpy as np
from sklearn import datasets
r =2# 筛选特征个数
X,y = datasets.load_iris(return_X_y =True)print('原始数据特征个数是:', X.shape[1])# 1、去中心化
mean_ = np.mean(X, axis=0)
X -= mean_
# 2、奇异值分解
u, s, v = np.linalg.svd(X)# 3、符号翻转(如果为负数,那么变成正值)
max_abs_cols = np.argmax(np.abs(u), axis =0)
display(max_abs_cols)
signs = np.sign(u[max_abs_cols,range(u.shape[1])])
display(signs)
u *= signs
# 4、降维特征筛选
u = u[:,:r]# 5、归一化
u =(u - u.mean(axis =0))/ u.std(axis =0, ddof =1)# ddof计算样本标准差
display(u[:5])print('经过PCA降维,数据特征个数是:', u.shape[1])

九、SVD进行矩阵求逆
9.1 SVD求逆矩阵原理
🚩在矩阵求逆过程中,矩阵通过
S
V
D
SVD
SVD 转换到正交空间。不同得奇异值和奇异值向量代表了矩阵中不同的线性无关(或独立)项。对矩阵进行
S
V
D
SVD
SVD 分解,形式如下所示:
A
m
×
n
=
U
m
×
m
∑
m
×
n
V
n
×
n
T
A_{m\times n}=U_{m\times m}\sum_{m\times n}V^T_{n\times n}
Am×n=Um×m∑m×nVn×nT
奇异值矩阵为:
∑
=
[
σ
1
σ
2
⋱
σ
n
]
\sum=\left[ \begin{matrix} \sigma_1 & & & \\ & \sigma_2 & & \\ & & \ddots & \\ & & & \sigma_n \\ \end{matrix} \right]
∑=⎣⎢⎢⎡σ1σ2⋱σn⎦⎥⎥⎤
当用
S
V
D
SVD
SVD 方法进行求逆时,会使得求逆运算变得非常简单,这是因为通过 SVD 求逆,只需要对奇异值求倒数即可,而左奇异矩阵
U
U
U 和右奇异矩阵
V
V
V 都是正交矩阵,有
U
−
1
=
U
T
U^{-1}=U^T
U−1=UT,
V
−
1
=
V
T
V^{-1}=V^T
V−1=VT 。因此,其求逆形式为:
(
A
m
×
n
)
−
1
=
(
U
m
×
m
∑
m
×
n
V
n
×
n
T
)
−
1
(A_{m\times n})^{-1}=(U_{m\times m}\sum_{m\times n}V^{T}_{n\times n})^{-1}
(Am×n)−1=(Um×m∑m×nVn×nT)−1
=
(
V
n
×
n
T
)
−
1
(
∑
n
×
m
)
−
1
(
U
m
×
m
)
−
1
=
(
V
n
×
n
)
(
∑
n
×
m
)
−
1
(
U
m
×
m
T
)
(V^T_{n\times n})^{-1}(\sum_{n\times m})^{-1}(U_{m\times m})^{-1}=(V_{n\times n})(\sum_{n\times m})^{-1}(U^T_{m\times m})
(Vn×nT)−1(∑n×m)−1(Um×m)−1=(Vn×n)(∑n×m)−1(Um×mT)
奇异值矩阵逆矩阵为:
[
σ
1
−
1
σ
2
−
1
⋱
σ
n
−
1
]
\left[ \begin{matrix} \sigma_1^{-1} & & & \\ & \sigma_2^{-1} & & \\ & & \ddots & \\ & & & \sigma_n^{-1} \\ \end{matrix} \right]
⎣⎢⎢⎡σ1−1σ2−1⋱σn−1⎦⎥⎥⎤
从上面可以看出,
S
V
D
SVD
SVD 求逆是原始奇异值的倒数,这就使得通过
S
V
D
SVD
SVD 对矩阵求逆变得非常简单:奇异值求倒数,奇异矩阵转置。
9.2 SVD求逆代码演示
import numpy as np
A = np.array([[3,4,5,5],[7,5,3,6],[6,5,7,7],[4,9,8,9],[5,10,5,7]])# A是奇异矩阵print('矩阵A的形状是:', A.shape)print('矩阵A的秩是:')
display(np.linalg.matrix_rank(A))
display(np.linalg.inv(A))# 无法直接求解逆矩阵

使用奇异值分解,进行逆矩阵求解
import numpy as np
import warnings
warnings.filterwarnings('ignore')
A = np.array([[3,4,5],[7,5,3],[6,5,7],[4,9,8],[5,10,5]])
u, s, v = np.linalg.svd(A)
display(u, s, v)
m, n = A.shape
# 奇异值求倒数# sigma = np.concatenate([np.diag(s),np.full(shape = (m-n,n),fill_value = 0)],axis = 0)# sigma = sigma**(-1)# cond = np.isinf(sigma)# sigma[cond] = 0
sigma = np.diag(np.concatenate([s**(-1),[0]*(m-n)]))[:,:3]# 逆矩阵求解
B = v.T.dot(sigma.T).dot(u.T)print('矩阵B是A的逆矩阵,两个进行矩阵运算得到单位矩阵:')
display(B.dot(A).round(5))

十、SVD进行协同过滤
10.1 协同过滤
🚩协同过滤是一种从大量用户给出的兴趣爱好集合中预测用户的偏好和兴趣的技术。 它的基本假设是,对某个事物,人们过去喜欢那么将来也会喜欢。 协作过滤可以用于推荐系统,该推荐系统自动向用户建议他/她的首选产品。
推荐系统的任务就是联系用户和信息,一方面帮助用户发现对自己有价值的信息,而另一方面让信息能够展现在对它感兴趣的用户面前,从而实现信息消费者和信息生产者的双赢。
10.2 干饭人
🚩下面是用户午餐点外卖倾向评分,分值
1
1
1**~**
5
5
5,分值越大表示倾向越大。
0
0
0 表示数据缺失,需要你使用
S
V
D
SVD
SVD 分解,将缺失值,进行补全,预测。数据如下:
外卖意向寿司牛肉拉面麻辣烫黄焖鸡米饭排骨饭张三21325李四35243王五13114赵六02452Michael44505Sara55231John11422Daniel24354Po13321辰chen50135
奇异值分解算法可以用于矩阵近似问题。如果分解时,中间的矩阵取部分特征值(只取前面若干个最大的特征值),这样就可以对原矩阵进行近似了。基于这种思想,奇异值分解可以用于预测用户对外卖点餐的倾向评分。
10.3 SVD进行协同过滤
import numpy as np
food = np.mat([[2,1,3,2,5],[3,5,2,4,3],[1,3,1,1,4],[0,2,4,5,2],[4,4,5,0,5],[5,5,2,3,1],[1,1,4,2,2],[2,4,3,5,4],[1,3,3,2,1],[5,0,1,3,5]])
u, sigma, v = np.linalg.svd(food)# 选取前2大特征值,做近似表达
food_result = np.mat(u[:,:2])* np.mat(np.diag(sigma[:2]))* np.mat(v[:2,:])
food_result.round(1)

根据SVD分解,对缺失值数据,进行了预测,结果如下:
外卖意向寿司牛肉拉面麻辣烫黄焖鸡米饭排骨饭张三21325李四35243王五13114赵六1.22452Michael4452.35Sara55231John11422Daniel24354Po13321辰chen51.4135
版权归原作者 辰chen 所有, 如有侵权,请联系我们删除。