数据预处理之数据清理，数据集成，数据规约，数据变化和离散化

本来这些储备知识，我想在后续的实际算法案例中进行解释，但是考虑到很多的小伙伴在学习的过程中都是逐步推进的，需要一定的时间去理解和应用，所以前期我们需要把所有的东西都准备好，这样就可以保证后续的算法实践游刃有余。

数据清理

我们一般看到的数据都是较为干净的数据，也就是结构化的数据，但是有时候在日志信息中，需要我们去提取出结构化的数据进行处理，这个时候就需要用到数据清理了。

数据清理用到的工具

1、Python

Python作为目前火热的编程语言，它的优势在于不需要编写大量的程序代码就可以实现我们所需的功能，而且在数据处理方面，Python的第三方库Pandas和Numpy有着不可描述的便捷性。

这也是我在概述篇里面介绍的需要准备的知识，同时在博主的文章里面也有比较详细的数据处理的文章，点击即可查看和学习。

2、Kettle

kettle作为ETL工具，可能很多人比较的陌生，这个工具在数据预处理方面有着比较好的优势，具有可重复性和简单性，由于它是一个图形界面的开发工具，不需要编程知识就可以完成，只需要明白每一步的过程和相应的按钮含义。

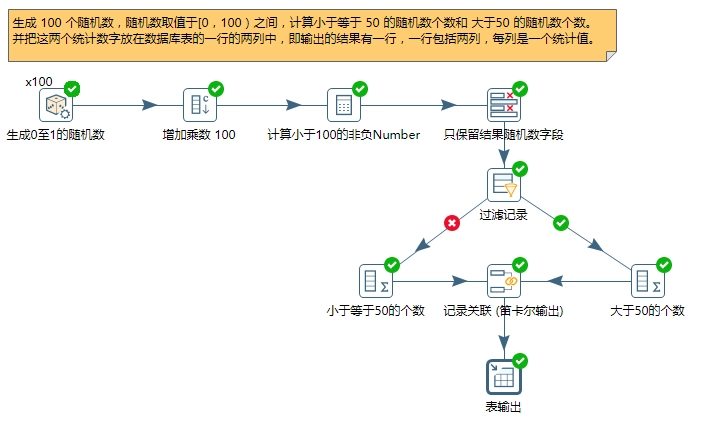
数据清理主要包括缺失值与异常值的清理

针对缺失值，可以采用简单的删除，但如果缺失值的比例达到一定阈值，就需要读者去判断是否在采集过程中出现了问题，不可以进行简单的删除操作了，因为一旦删除了数据，数据所代表的信息就无法找回了。

也可以将缺失值添加成默认值，或是采用拉格朗日插值法对缺失值进行填充等方式。

在Pandas里面有很多种对缺失值的处理办法，还可以使用左右填充的方法以及上下填充，也可以按照某一列的统计量进行填充，还可以填充特定规则的数据，下面给出具体的代码实现

检测出空值

# 检测出有空值的行数据
df[df.isnull().T.any()]

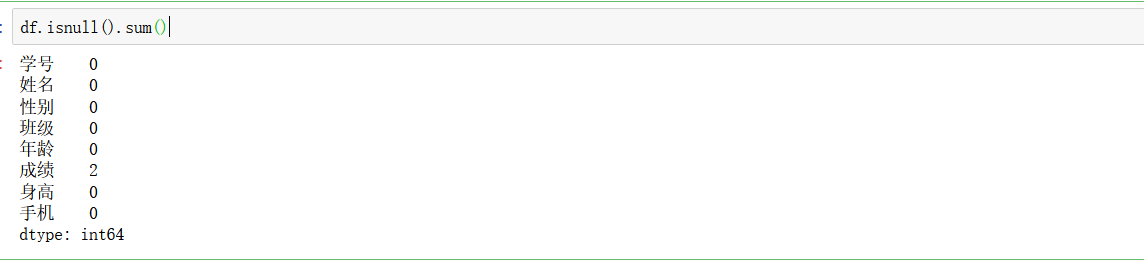
直接删除

df.dropna()
# 删除包含空值的所有行

df.dropna(axis=1)
# 删除包含空值的所有列

# 删除一行全部是空值的数据行
df.dropna(how="all")

df.dropna(how="all",axis=1)
# 删除列数据里面全部是空值的列

填充处理

# 通过给定的数据填充，一般是0
df.fillna(0)

指定我们的数据列，进行填充
df[["成绩"]].fillna(100)

# 指定数据列按照平均值进行填充
df[["成绩"]].fillna(round(df["成绩"].mean(),2))
# 这里的平均值可以替换成最大值max，最小值min，以及各种的统计函数

前后左右值填充

# 使用前后左右的值来填充
# 上面的值 forwardfill 列上前一个值
df[['成绩']].fillna(method="ffill")

# 下面的值 backfill 列上后一个值
df.fillna(method="bfill")

# 左边的值 forwardfill 行上前一个值
df.fillna(method="ffill", axis=1)

# 右边的值 backfill 行上后一个值 
df.fillna(method="bfill", axis=1)
# 如果超过边界无法取值

这里需要注意一下，有些时候由于边界的原因，无法填充，那么可以先使用某一个填充然后再去使用另外一个填充模式，这样全方位的填充，效果比较的好！

数据集成

主要是指将多种数据源汇集到一起，放入一个数据仓库的过程。在数据集成的过程中会出现实体识别(Entity Resolution)，冗余属性识别，数据值冲突等问题。

在将多种数据源集成时，实体识别是很常见的事情，实体识别可描述成：在一个或多个数据源中的不同记录是否描述为同一个实体， 同一实体在数据集成过程中可被用于数据去重和连接键等集成操作中。

用一个数据库中的实例就是，如果 A 表中有一个字段为 stu_id， B 表中有一个字段为 stu_num，那么这两个字段是否都为同一个实体的属性呢？

如果是同一个属性，那么在集成时，这个这段可以作为多表关联的条件，生成新表时保留两者中的一个值就可以。

冗余属性识别是指是否某些属性之间存在相关性，或者一个属性可以由其它的属性推导得出。数据值冲突指的是不同数据源中针对同一个实体的属性值不同，这可能是单位不一致导致的。

数据集成就是在多种数据源的集成过程中，解决掉上述的几个问题，形成一个大的不冗余的数值清楚的数据表。
说到数据集成，一般用于大量的数据维度的例子，比如某电商的售卖系统所产生的数据，这里就需要考虑到数据里面的范式了，在我的《数据库技术原理应用-计算机三级》可以看到具体的解释，点击蓝色字体即可跳转。

数据规约

是指在保证原始数据信息不丢失的前提下，减少分析使用的数据量，数据规约中最常使用的方式是维规约。

维规约的含义是从将原先高维的数据合理的压缩成低维数据，从而减少数据量，常用的方法为特征的提取， LDA 和 PCA 降维。特征的提取为从海量数据中选择与挖掘目标相关的属性成一个子表，不包含无关的属性，比如关于泰坦尼克号生产数据的数据挖掘中，船客 Name 与幸存率是无关的，就可以不放入子表中。

PCA 是基于方差的聚类降维， LDA 是基于有监督的降维，都可以对高维数据进行降维。假定某公司进行一次知识发现的任务，选取的数据集为数据仓库中的全部数据（数据量基本在数 T 以上），固然这样可以获得的数据是最完整的，但由于数据仓库中的数据是非常大的，在如此大的数据集上进行复杂且存在迭代计算的数据分析，所要花费的时间是很长的，分析一个结果可能需要一个月的时间，时间不满足用户的需求，使得这种全量数据的分析是不可行。

数据归约技术采用维规约和数据量规约等方式，可以对数据仓库中的海量数据进行提取，获得较小数据集，仍可大致保留原数据的完整性。这样，完成一个效率和效果的兼顾，在允许的时间内完成数据挖掘任务。

数据的变换

是将原始的特征数据进行归一化和标准化的操作。

归一化是将原始数值变为（0，1）之间的小数，变换函数可采用最小最大规范化等方法。

标准化是将数据按比例缩放，使之落入一个小的特定区间，常用的函数为是 z-score 标准化，处理后的均值为 0，标准差为 1，一般标准化要求原始数据近似符合高斯分布。

归一化的原因在于不同变量往往量纲不同，归一化可以消除量纲对最终结果的影响，使不同变量具有可比性。数据挖掘过程中，数值较大的特征，会被算法当成权重较大，但实际情况是数值较大，并不一定代表该特征更重要，归一化和标准化后的数据可以避免这个问题的出现。

数据离散化可通过聚类，直方图，分箱等方式完成数据的离散化。

下面介绍一下具体的实现方法以及原理

1、Min-Max 规范化 [0,1]规划

Min-max 规范化方法：将原始数据变换到[0,1]的空间中。让原始数据投射到指定的空间

[min, max]，用公式表示就是：新数值 =（原数值 - 极小值）/（极大值 - 极小值）。

• 定义：也称为离差标准化，是对原始数据的线性变换，使得结果映射到0-1之间。
• 本质：把数变为【0,1】之间的小数。
• 转换函数：（X-Min）/(Max-Min)
• 如果想要将数据映射到-1,1，则将公式换成：（X-Mean）/(Max-Min)

from sklearn import preprocessing
import numpy as np
 
# 初始化数据，每一行表示一个样本，每一列表示一个特征
x = np.array([
    [0.,-3.,1.],
     [3.,1.,2.],
     [0.,1.,-1.]
     ])
# 将数据进行 [0, 1] 规范化
min_max_scaler = preprocessing.MinMaxScaler()
min_max_x = min_max_scaler.fit_transform(x)
 
print(min_max_x)

2、Z-Score 规范化

Z-Score 的方法：新数值 = （原数值 - 均值）/ 标准差。

• 定义：这种方法给与原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1.
• 本质：把有量纲表达式变成无量纲表达式。
• 转换函数：（X-Mean）/(Standard deviation)

假设 小明 所在的班级平均分为 80，标准差为 10。小华 所在的班级平均分为 120，标准差为 100。那么 小明 的新数值 =(80-80)/10=0，小华 的新数值 =(80-120)/100=-0.4。那么在 Z-Score 标准下，如果小明和小华的成绩都是80，小明 的成绩会比 小华 的成绩好。

因此，我们能看到 Z-Score 的优点是算法简单，不受数据量级影响，结果易于比较。不足在于，它需要数据整体的平均值和方差，而且结果没有实际意义，仅是用于比较！！！

注意是每一个算法都需要使用归一化，标准化吗？

答案不是的，如果考虑的是距离还不是相似度函数那么就需要，反之则需要；例如：随机森林，它从不比较一个特征与另一个特征，不许要规范化。

归一化后加快了梯度下降求最优解的速度。

归一化有可能提高精度（归一化是让不同维度之间的特征在数值上有一定的比较性）。

两种归一化方法的使用场景：

（1）在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

第一种方法(线性变换后)，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。

（2）在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在（0 ，255）的范围。

第二种归一化方式中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。

通常情况下，如果使用下面的库

from sklearn.preprocessing import MinMaxScaler,MaxAbsScaler,StandardScaler
#最大最小[0,1]
#[-1,1]
#去均值化

注意：归一化适用于相似函数，标准化适用于距离度量情况

正则化

正则化主要用于避免过拟合的产生和减少网络误差。

常见的有正则项有 L1 正则 和 L2 正则 以及 Dropout ，其中 L2 正则 的控制过拟合的效果比 L1 正则 的好。

• L1正则化可以产生稀疏解，即会使得很多参数的最优值变为0，以此得到的参数就是一个稀疏矩阵或者向量了。可以用于特征选择。
• L2正则化可以产生值很小的参数，即会使得很多参数的最优值很小。可以防止模型过拟合。

简单来说L1适合用于特征选取，降低模型的复杂度；L2可以解决模型的过拟合。那么也就是说你可以这样去理解，L1适用于特征较多的情况下

特征选择： 它会让模型参数向量里的元素为0的点尽量多。 因此可以排除掉那些对预测值没有什么影响的特征，从而简化问题。所以 L1 范数解决过拟合措施实际上是减少特征数量。
可解释性： 模型参数向量稀疏化后，只会留下那些对预测值有重要影响的特征。 这样我们就容易解释模型的因果关系。 比如针对某个癌症的筛查，如果有100个特征，那么我们无从解释到底哪些特征对阳性成关键作用。 稀疏化后，只留下几个关键特征，就更容易看到因果关系

最后给大家分享一张，机器学习必看到的一张图

每文一语

每个人都有选择自己生活的权利