各位小伙伴们,大家好,我是在研途中探索的小曾哥,首先祝大家端午安康,节日快乐!在此节日,特意奉上一篇序列推荐的文章,干货满满,与各位共勉。
题目:Sequential Recommendation for Cold-start Users with Meta Transitional Learning发表在2021年SIGIR上
文章目录
Abstract
老样子,见摘要如洞悉全文,需要带着问题来看:
1、解决了什么问题?【或者目前算法的局限性】
2、用了什么方法?【重点】
3、实验效果如何?【优势】
介绍:顺序推荐器的一个基本挑战是捕捉用户的顺序模式,以建模用户在项目之间的传输方式。
存在问题:在许多实际场景中,有大量的冷启动用户只记录了最少的交互。 结果,现有的顺序推荐模型将失去其预测能力,因为难以在仅具有有限交互的用户上学习顺序模式。
本论文贡献:使用一个名为 MetaTL 的新框架来改进冷启动用户的顺序推荐,该框架通过元学习来学习对用户的转换模式进行建模。
贡献: (ii) 使用基于翻译的架构提取用户之间的动态转换模式; (iii) 采用元过渡学习,使只有有限交互的冷启动用户能够快速学习,从而准确推断顺序交互。
Background
在此跟大家介绍一下元学习的内容和基于“翻译”的序列推荐,了解这些内容会加深对文章的理解,看文章也会事半功倍
元学习
之前写过一篇非常详细的文章,如果对这个元学习不熟悉, 可以转看元学习入门必备:MAML(背景+论文解读+代码分析)
目前这块主要是介绍元学习和小样本学习之间关系:一般用到元学习方法来解决小样本问题,通过少量样本从而更快的进行学习。 通过上图来介绍一下原因:在训练阶段学到了一个整体的能力F,在元学习测试阶段,还是需要对应的支持集(support set),这样才能根据支持集获取对应任务的f.
MAML
MAML是元学习的经典实现算法,已经广泛的用于各个领域,目前引用量也达到了6000+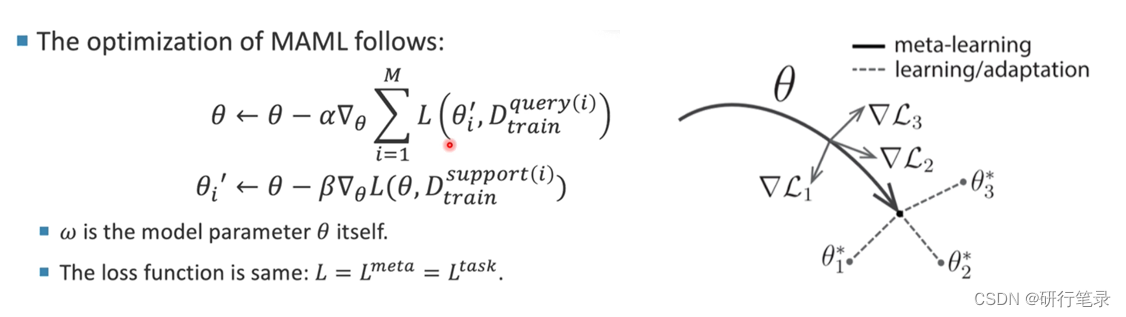
元学习的变体:1、在上式中,将w算法替换成θ,其实就是学习一个比较好的初始值 ;2、在MAML中 loss函数在
L
=
L
meta
=
L
task
L=L^{\text {meta }}=L^{\text {task }}
L=Lmeta =Ltask
主要目的是:根据loss值得到对应的更新方向,最终经过一步更新后,获得一个比较好的初始值。
Translation-based recommendation
这是序列推荐中比较经典的方法,translation-based recommendation是ACM RecSys’ 17最佳论文奖。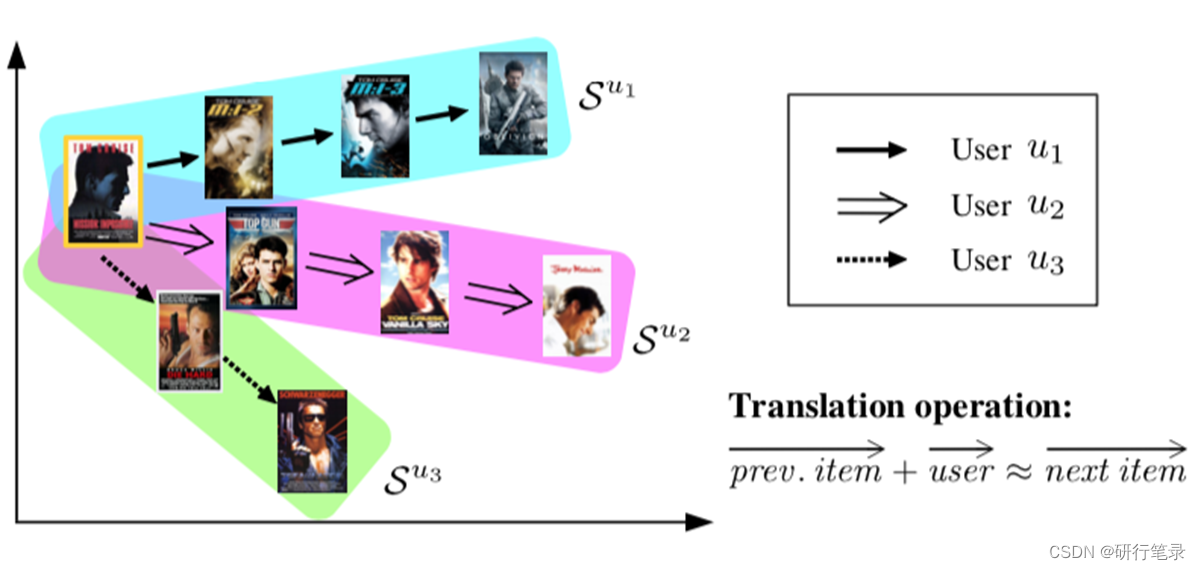
以上述的例子来进行解释:首先将左边电影嵌入到翻译空间中,然后用户1的记录是看的电影第一部,那么预测用户1的下一个记录是第二、第三部;对于用户2而言,知道用户的偏好是演员,那么预测下一个序列是对应演员的电影;对于用户3而言,主要是对电影类型感兴趣,那么下一个交互就是对应的动作片。
因此这篇文章的基本思路是用户对应的向量和用户上一个交互过的物品向量之和,要和用户下一个要交互的物品向量在距离上相近。 主要就是理解这个公式:
prev. item
→
+
user
→
≈
next item
→
\overrightarrow{\text { prev. item }}+\overrightarrow{\text { user }} \approx \overrightarrow{\text { next item }}
prev. item + user ≈ next item
Introduction
主要就是介绍背景,现有方法缺点,引出动机,提出贡献
推荐系统在将用户与他们在许多大型在线平台上喜欢的内容联系起来方面发挥着重要作用。 与对用户的一般偏好建模的传统推荐系统 不同,顺序推荐系统 旨在从用户的行为序列中推断出用户的动态偏好。
然而,在许多现实世界的场景中,顺序推荐器在处理与系统交互有限的新用户时可能会面临困难,从而导致固有的长尾交互数据 [35]。 理想情况下,一个有效的推荐系统应该能够向与项目只有少量交互的新用户推荐项目。 然而,由于难以用有限的数据来表征用户偏好,大多数现有的顺序推荐器并不是为处理这种冷启动用户而设计的。 由于新用户最初收到的推荐不佳可能会离开平台,因此如何捕捉这些冷启动用户的偏好成为构建令人满意的推荐服务的关键问题。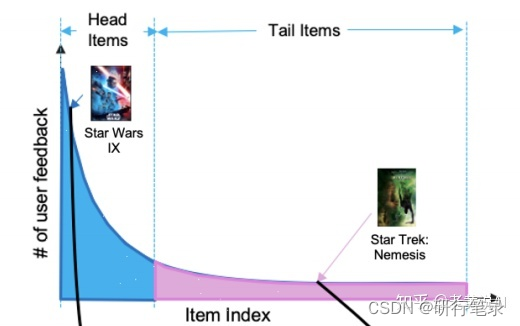
尽管已经提出了很多冷启动推荐方法,但大多数在训练期间需要辅助信息 或来自其他领域的知识 ,并且通常将用户-项目交互处理为静态 方式。 相比之下,冷启动顺序推荐针对的是由于隐私问题而无法访问额外辅助知识的设置,更重要的是,用户-项目交互是顺序依赖的。 用户的偏好和品味可能会随着时间而改变,这种动态对于顺序推荐具有重要意义。 因此,有必要开发一种新的顺序推荐框架,该框架可以提取短程项目过渡动态,并快速适应那些用户与项目交互有限的冷启动用户。
在这项工作中,我们提出了一种称为 MetaTL 的新元学习框架,用于解决冷启动顺序推荐的问题。 为了仅通过少量用户-项目交互来提高模型泛化能力,我们将冷启动顺序推荐的任务重新表述为小样本学习问题。 与直接在数据丰富的用户上学习的现有方法不同,MetaTL 构建了一个模仿目标冷启动场景的少样本用户偏好转换任务池,并以元学习的方式逐步学习用户偏好。 此外,我们在基于翻译的架构之上构建了所提出的框架,这使得推荐模型能够有效地捕捉短程过渡动态。 这样元学习的顺序推荐模型可以从那些数据丰富的用户中提取有价值的过渡知识,并快速适应冷启动用户以提供高质量的推荐。 这项工作的贡献可以总结如下:
辅助信息:用户的商品消费历史记录
- 我们探索的具有挑战性的问题顺序推荐为预热将用户不依赖辅助信息并提出制定few-shot学习问题
- 我们开发了一种新颖的元学习范式——MetaTL 来对用户的转换模式进行建模,它可以快速适应冷启动用户来推断他们的顺序交互。
- 通过对三个真实世界数据集的大量实验,我们验证了所提出的 MetaTL在冷启动顺序推荐中的有效性,并表明与顺序推荐中的最新技术相比,它可以带来 11.7% 和 5.5% 的改进 和冷启动用户推荐。
Related work
主要介绍目前已有的方法,进行分类描述,进一步引出本文的motivation
顺序推荐
顺序推荐的第一种方法是使用马尔可夫链来建模用户在项目之间的转换[21]。 最近,TransRec [7] 将项目嵌入到“过渡空间”中,并为每个用户学习一个翻译向量。 随着神经网络的进步,许多不同的神经结构,包括循环神经网络 [9, 10]、卷积神经网络 [25, 36]、变压器 [12, 24] 和图神经网络 [31, 34],已被用于 对用户对其行为序列的动态偏好进行建模。 虽然这些方法旨在通过对序列的表示学习来提高整体性能,但对于行为序列较短的冷启动用户,它们的预测能力较弱。
元学习
这一系列研究旨在学习一个模型,该模型可以通过少量训练样本适应和泛化到新任务和新环境。 为了实现“learning-to-learn”的目标,有三种不同的方法。
基于度量的方法基于与最近邻算法类似的思想,具有精心设计的度量或距离函数 [28]、原型网络 [3、23] 或连体神经网络 [13]。
基于模型的方法通常使用内部架构执行快速参数更新,或者由另一个元学习器模型控制 [22]。
对于基于优化的方法,通过调整优化算法,可以通过几个示例有效地更新模型 [4, 5, 18]。
在这项工作中,我们探索了如何设计一种有效的方法来处理短序列的冷启动顺序推荐。
冷启动推荐
在新用户或项目没有可用历史交互的完整冷启动设置下,以前的工作通常会学习辅助信息与训练有素的潜在因素之间的转换[6,15,26]。 在不完全冷启动设置下,Dropoutnet 利用 Dropout 层来模拟数据丢失问题 [29]。 同时,元学习已被用于训练针对冷启动案例量身定制的模型。 为了解决用户冷启动问题,MetaRec [27] 提出了一种元学习策略来学习用户特定的逻辑回归。 还有 MetaCF [33]、Warm-up [19] 和 MeLU [14] 等方法,采用与模型无关的元学习 (MAML) 方法来学习模型,以实现对冷启动用户的快速适应。 然而,它们都没有在设计时考虑到用户偏好的动态(如顺序推荐中的情况)。
模型
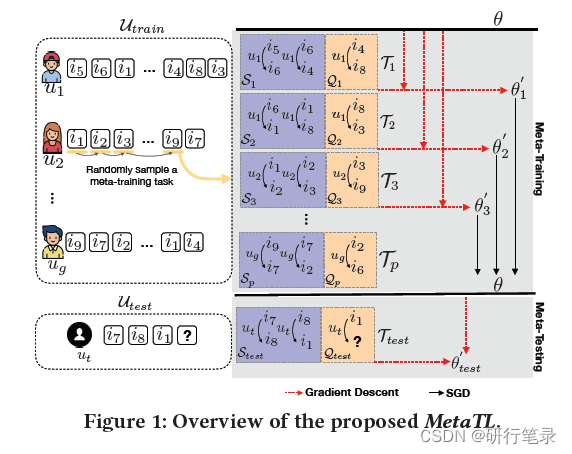
上图是本篇文章的Overview,主要就是MAML的思想过程。
1、首先将训练数据分为训练集的支持集(support_set)和查询集(query_set)。将不同的学生作为不同的任务,以用户1为例,根据前一个序列i5,加上用户的行为偏好,那么下一个序列就是i6,充分学习这些序列关系,通过损失函数得到
θ
1
′
\theta_{1}^{\prime}
θ1′,同理根据不同的学生得到
θ
2
′
\theta_{2}^{\prime}
θ2′、
θ
3
′
\theta_{3}^{\prime}
θ3′,然后在查询集中验证更新后的
θ
′
\theta^{\prime}
θ′,最终通过梯度下降获得θ。
2、在测试阶段,根据查询集中几条记录,得到
θ
test
′
′
\theta_{\text {test }}^{\prime \prime}
θtest ′′,然后来预测u_{t}的下一个序列是什么。
具体细节如下
问题定义
Seq
u
=
(
i
u
,
1
,
i
u
,
2
,
…
,
i
u
,
n
)
\operatorname{Seq}_{u}=\left(i_{u, 1}, i_{u, 2}, \ldots, i_{u, n}\right)
Sequ=(iu,1,iu,2,…,iu,n)
预测每个候选人的偏好得分项基于Seq,因此建议头n个得分最高的项目。
在我们的任务中,训练Utrain ,包含用户的各种数字的记录交互,然后给出测试集Utest,该模型可以快速学习用户过渡模式根据퐾最初的交互,从而推断出连续的相互作用。
现在设置(2/3/4) 为冷启动情况 【将冷启动问题定义为小样本问题】
MTL(meta transitional learning)
RQ1:如何使模型能够将知识从数据丰富的用户转移到冷启动用户?
小样本连续推荐
元学习旨在通过一些训练样本来学习一种能够适应新任务(即新用户)的模型。为了实现冷启动用户序贯推荐中的元学习,我们通过对多个采样相似任务(即元训练任务)的训练,将序列推荐作为一个新的小样本学习问题(即元测试任务)进行训练。
初始交互顺序:
i
A
⟶
u
j
i
B
⟶
u
j
i
C
i_{A} \stackrel{u_{j}}{\longrightarrow} i_{B} \stackrel{u_{j}}{\longrightarrow} i_{C}
iA⟶ujiB⟶ujiC
获得过渡对:
i
A
⟶
u
j
i
B
,
i
B
⟶
u
j
i
C
i_{A} \stackrel{u_{j}}{\longrightarrow} i_{B}, i_{B} \stackrel{u_{j}}{\longrightarrow} i_{C}
iA⟶ujiB,iB⟶ujiC
预测查询集:
i
C
⟶
u
j
?
i_{C} \stackrel{u_{j}}{\longrightarrow} ?
iC⟶uj?
我们如何从数据丰富的用户生成一个元训练任务池来模拟目标冷启动场景?
任务:预测冷启动用户的初始交互,预测K+1
1、从用户的日志交互中随机选择一个用户,并随机抽取k+1交互
2、获得k+1交互顺序 : 支持集
i
1
⟶
u
j
i
2
,
i
2
⟶
u
j
i
3
,
i
K
−
1
⟶
u
j
i
K
i_{1} \stackrel{u_{j}}{\longrightarrow} i_{2}, i_{2} \stackrel{u_{j}}{\longrightarrow}{i_{3}},i_{K-1} \stackrel{u_{j}}{\longrightarrow}{i_{K}}
i1⟶uji2,i2⟶uji3,iK−1⟶ujiK 查询集
i
K
⟶
u
j
i
K
+
1
i_{K} \stackrel{u_{j}}{\longrightarrow} i_{K+1}
iK⟶ujiK+1
RQ2:我们如何捕捉用户-项目交互序列中的短程转换动态?
元过渡学习
我们的目标是获得学习转换模式的能力,以帮助预测只需几次初始交互的新用户的下一次交互。
1、希望使用支持集Sn中的过渡对来检索过渡动态 【
i
h
⟶
u
j
i
t
i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}
ih⟶ujit】
2、然后我们可以使用简单的MLP网络来表示具有iℎ和项it的过渡信息(W和b表示可训练的变换矩阵和偏差向量)
t
h
,
t
=
σ
(
W
(
i
h
∥
i
t
)
+
b
)
\mathbf{t}_{h, t}=\sigma\left(\mathbf{W}\left(\mathbf{i}_{h} \| \mathbf{i}_{t}\right)+\mathbf{b}\right)
th,t=σ(W(ih∥it)+b)
3、由于在当前任务Tn的支持集Sn中有多个转移对,我们需要聚集来自所有对的转移信息以生成最终的表示trn,我们取支持集Sn中每个转换对的所有转换信息的平均值
tr
n
=
1
∣
S
n
∣
∑
(
i
h
⟶
u
j
i
t
)
∈
S
n
t
h
,
t
\operatorname{tr}_{n}=\frac{1}{\left|\mathcal{S}_{n}\right|} \sum_{\left(i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}\right) \in \mathcal{S}_{n}} \mathbf{t}_{h, t}
trn=∣Sn∣1(ih⟶ujit)∈Sn∑th,t
4、需要一个评分函数来评估它在刻画用户转换模式方面的有效性:基于翻译的推荐中的思想,用户可以被视为交互序列中两个连续项目之间的翻译。
s
(
i
h
⟶
u
j
i
t
)
=
∥
i
h
+
tr
n
−
i
t
∥
2
s\left(i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}\right)=\left\|\mathbf{i}_{h}+\operatorname{tr}_{n}-\mathbf{i}_{t}\right\|^{2}
s(ih⟶ujit)=∥ih+trn−it∥2然后我们根据支持集
S
n
\mathcal{S}_{n}
Sn 中**所有过渡对计算边际损失**为:
L
S
n
=
∑
(
i
h
⟶
u
j
i
t
)
∈
S
n
[
γ
+
s
(
i
h
⟶
u
j
i
t
)
−
s
(
i
h
⟶
u
j
i
t
′
)
]
+
\mathcal{L}_{S_{n}}=\sum_{\left(i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}\right) \in \mathcal{S}_{n}}\left[\gamma+s\left(i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}\right)-s\left(i_{h} \stackrel{u_{j}}{\longrightarrow} i_{t}^{\prime}\right)\right]_{+}
LSn=(ih⟶ujit)∈Sn∑[γ+s(ih⟶ujit)−s(ih⟶ujit′)]+
RQ3:如何优化元学习器以便为冷启动用户做出准确的推荐? [MAML]
解释了优化模型的过程,以便它可以通过几次交互来学习新用户的过渡模式
元模型表示:f(θ)
我们希望模型可以在Lsn中获得一个较小的值,因此我们通过使用一个梯度步长最小化Lsn来更新模型f(θ):
θ
n
′
=
θ
−
α
∇
θ
L
S
n
(
f
θ
)
\theta_{n}^{\prime}=\theta-\alpha \nabla_{\theta}\mathcal{L}_{\mathcal{S}_{n}}\left(f_{\theta}\right)
θn′=θ−α∇θLSn(fθ)
其中α是任务学习率
其中P(T)是元训练任务的分布,可以通过随机抽样元训练任务来获得。要求解该方程,我们可以通过随机梯度下降(SGD)进行优化,从而:
θ
←
θ
−
β
∇
θ
∑
T
n
∼
p
(
T
)
L
Q
n
(
f
θ
n
′
)
\theta \leftarrow \theta-\beta \nabla_{\theta} \sum_{\mathcal{T}_{n} \sim p(\mathcal{T})} \mathcal{L}_{Q_{n}}\left(f_{\theta_{n}^{\prime}}\right)
θ←θ−β∇θ∑Tn∼p(T)LQn(fθn′)
Experiment
数据集
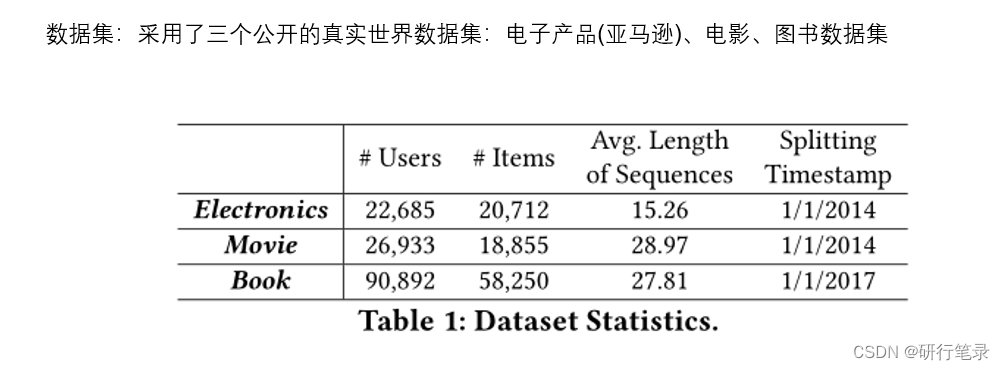
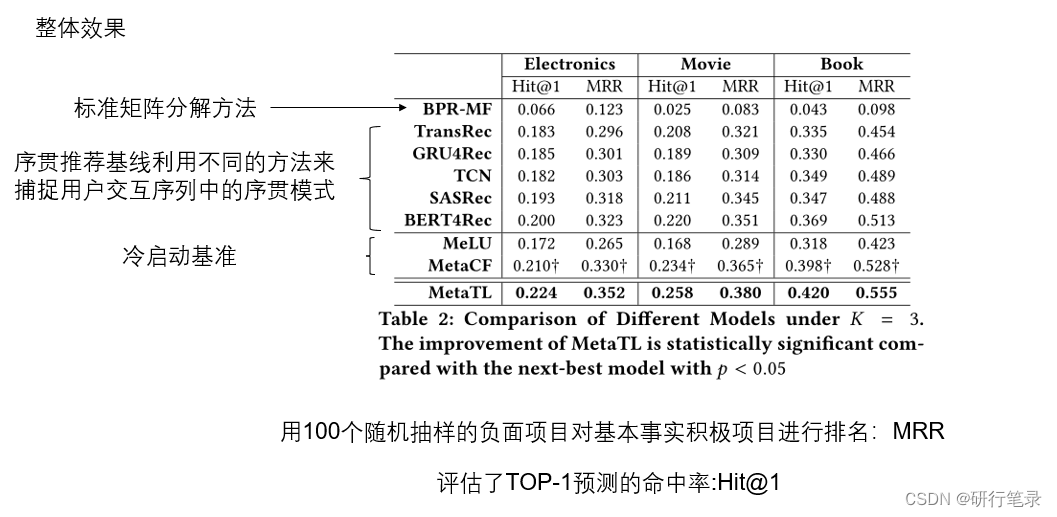
整体效果
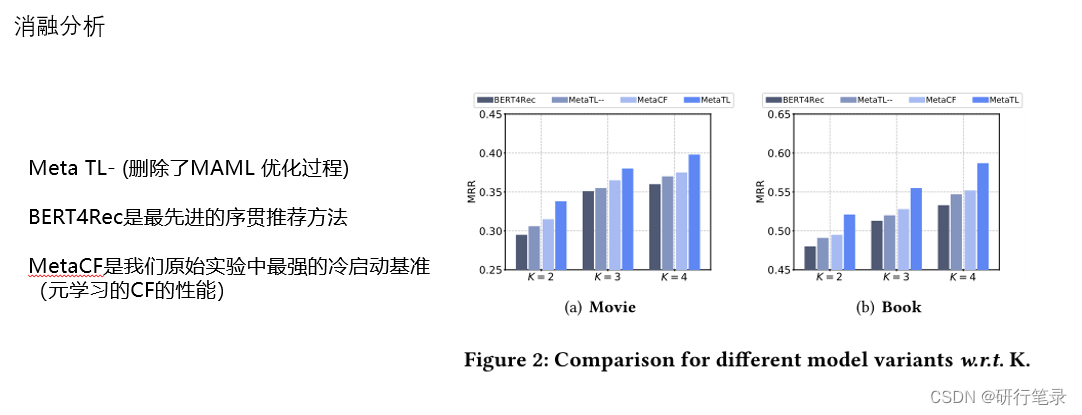
消融分析
本篇文章也是前一段时间所记录的笔记,希望能够给各位小伙伴们提供一些帮助!
研途漫漫,小曾哥与你们同行!
版权归原作者 研行笔录 所有, 如有侵权,请联系我们删除。