第29次CCF CSP 认证题目 第一题 202303-1 田地丈量 C++实现 满分答案

问题描述

西西艾弗岛上散落着 n 块田地。每块田地可视为平面直角坐标系下的一块矩形区域，由左下角坐标 (x1,y1) 和右上角坐标 (x2,y2) 唯一确定，且满足 x1<x2、y1<y2。这 n 块田地中，任意两块的交集面积均为 0，仅边界处可能有所重叠。

最近，顿顿想要在南山脚下开垦出一块面积为 a×b 矩形田地，其左下角坐标为 (0,0)、右上角坐标为 (a,b)。试计算顿顿选定区域内已经存在的田地面积。

输入格式

从标准输入读入数据。

输入共 n+1 行。

输入的第一行包含空格分隔的三个正整数 n、a 和 b，分别表示西西艾弗岛上田地块数和顿顿选定区域的右上角坐标。

接下来 n 行，每行包含空格分隔的四个整数 x1、y1、x2 和 y2，表示一块田地的位置。

输出格式

输出到标准输出。

输出一个整数，表示顿顿选定区域内的田地面积。

样例输入

4 10 10
0 0 5 5
5 -2 15 3
8 8 15 15
-2 10 3 15

Data

样例输出

44

Data

样例解释

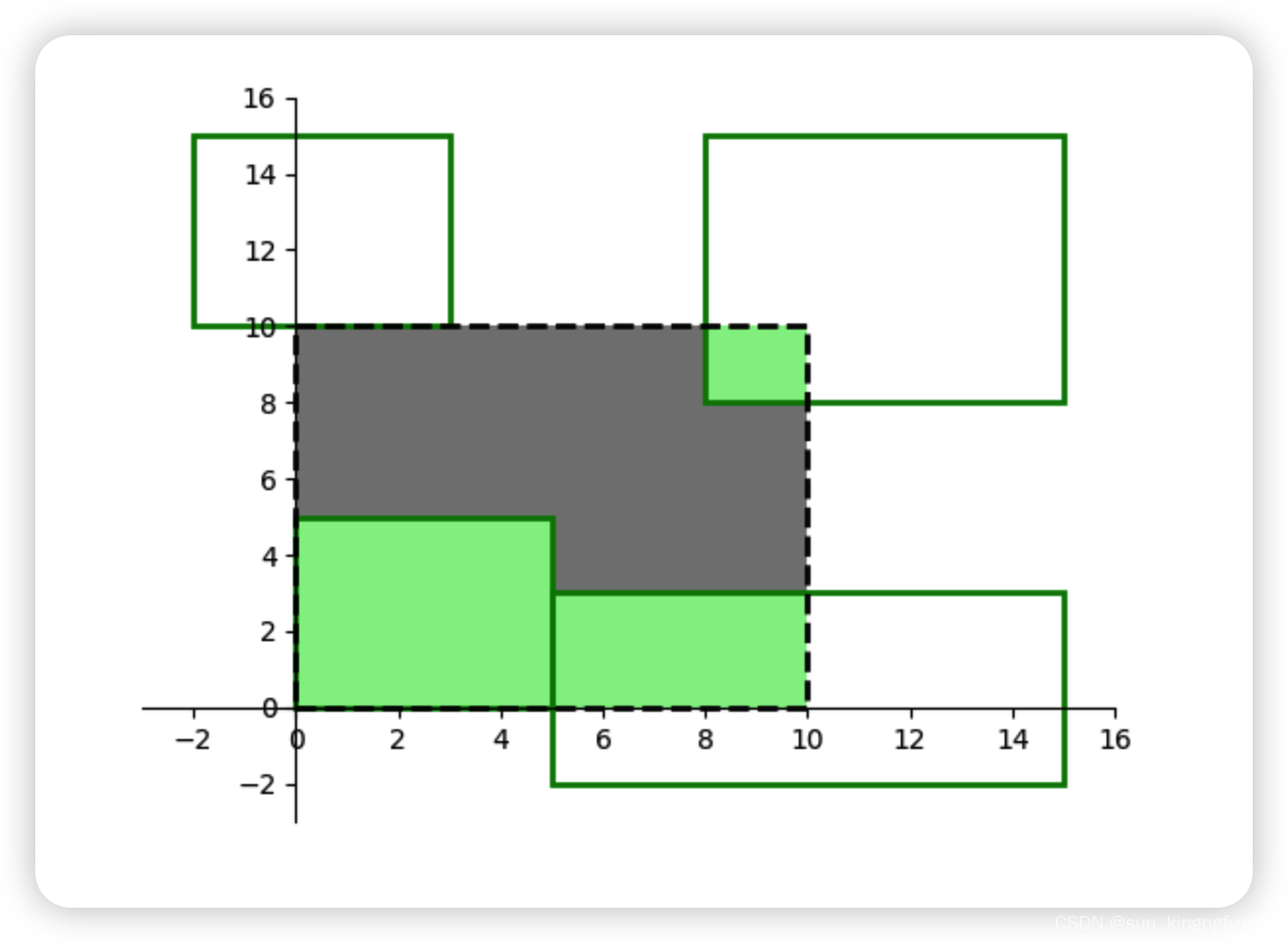
如图所示，选定区域内田地（绿色区域）面积为 44。

子任务

全部的测试数据满足 n≤100，且所有输入坐标的绝对值均不超过 104。

解题思路：

本质是求矩阵之间的交集面积，通过画图观察找出规律。交叉部分面积（以两个矩形为例），交叉部分矩阵右边界即原两个大矩阵的右边界中的较小值，左边界即原两个大矩阵的左边界中的较大值。因此，交叉矩阵的宽即为右边界减去左边界x = min(a, x2) - max(0, x1);同理可得上边界和下边界的关系 y = min(b, y2) - max(0, y1);最后，通过判断x 和 y是否大于零，从而判断两个矩阵之间是否存在交叉部分，若存在则 sum += x * y;

C++ 满分代码如下：

#include <iostream>

using namespace std;

int main()
{
int n, a, b;
int x1, y1, x2, y2;
int x, y;
int sum = 0;
cin >> n >> a >> b;
for(int i = 1; i <= n; i++){
cin >> x1 >> y1 >> x2 >> y2;
x = min(a, x2) - max(0, x1);
y = min(b, y2) - max(0, y1);
if(x >= 0 && y >= 0)
sum += x * y;
}
cout << sum;
return 0;
}

总结

作为CCF CSP认证考试第一题一般代码量不会很长，for循环一般也只有一层，注意观察总结规律，提炼抽象模型。该题存在部分同学使用大量if语句进行条件判断的写法，耗时且容易遗漏，正确率较低，从而第一题心态崩溃，影响后续题目发挥，注意不要死磕，及时转换战术。