机器学习期末复习

概述

机器学习的三步骤

1.定义一个function set
2.找一个评价标准
3.挑选出最好的一个function

semi-supervised Learning

既有labelled data也有unlabelled data，并且还有一些与任务无关的data

Alpha go

Alpha go是监督学习+强化学习

机器学习与人工智能、深度学习三者的关系

人工智能：机器展现出的人类智能
机器学习：计算机利用已有的数据，得出了某种模型，并利用该模型预测未来的一种方法。（实现人工智能的方法）
深度学习：实现机器学习的一种技术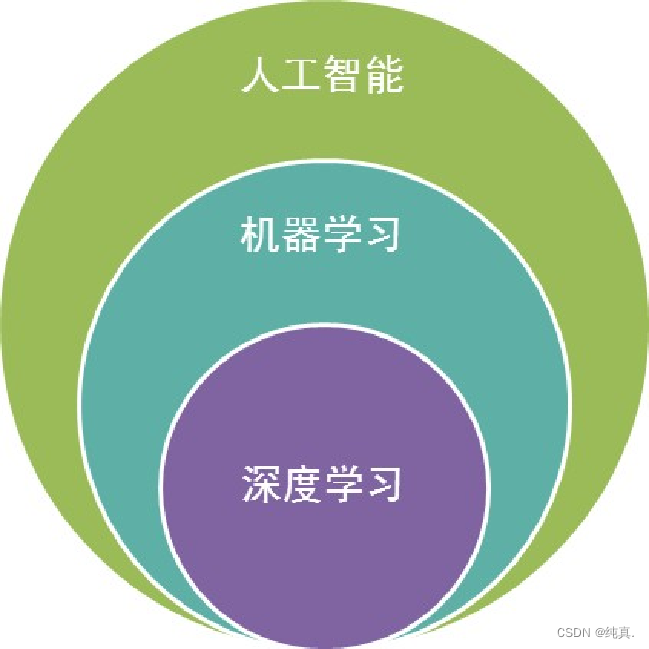

机器学习与人工智能、深度学习三者的区别

深度学习的计算量更大，而机器学习技术通常更易于使用。

回归

basic

回归是一种prediction，他的输出是一个数量。比如预测房价，预测股市等。

事例（预测CP值）

step1：建立模型

建立模型，假设建立线性模型，y=wx+b。
其中b是bias，w指的是weight。

step2：goodness of function set

这里采用一种Loss function进行评估，他的输入是一个函数，其实就是输入w和b，输出是一个指标。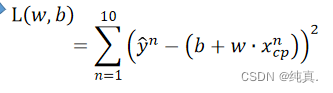
这里计算预测值与实际值之间的差值平方和进行计算，其实就是估算误差。

step3：挑选最好的function

最好的function即找到一组参数w，b使得Loss的值最小。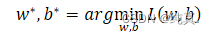
采用gradient descent即梯度下降的方法进行寻找。

梯度下降

这里仅以单变量为例进行说明，即计算w*=argminL（w）。

起始步骤

首先需要选取一个初始值w0，而后计算此处的梯度值，若此处的值为正，那么需要减小w的值；反之则需要增大w的值。

参数更新

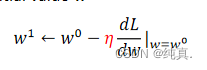η 是学习率（控制学习快慢的参数），可以看出学习率越大参数更新的将会更快一些，但可能会略过一些最优解。
线性模型中不存在局部最小值，但其他模型中可能会有因local minimal导致无法找到global minimal的情况。

两个参数的情况

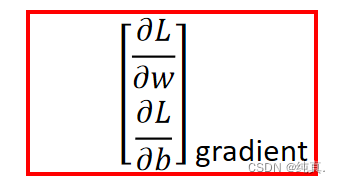其实情况类似，只是将参数变多，而后分别进行更新，这里需要计算梯度。

结果如何呢？

刚才只是讨论了线性的模型，若将模型扩展到高次的情况继续分析，将会发现模型越复杂，在训练集上的效果将会越好，但这在测试集上效果却不一定更优。
这是因为存在一个过拟合的情况，overfitting。

过拟合（overfitting）

关于overfitting的问题，很大程度上是由于曲线为了更好地拟合training data的数据，而引入了更多的高次项，使得曲线更加“蜿蜒曲折”，反而导致了对testing data的误差更大

正则化（regularization）

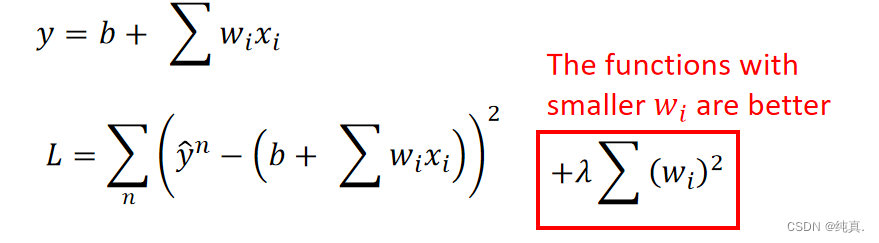λ越大函数将会越平滑，因为他会使得wi变小，权重越小那么每个因素对模型的单体影响将会变小，从而更关注整体。但也不能太过平滑。

为什么平滑的函数会表现的更好

当收到一些噪声干扰时，模型会收到较小的影响，得到一个较好的结果。λ越大在training data上的error会越大，但在testing data上可能会变好，这是因为正则化以后更多关注权重，就会更少关注error。

过拟合和正则化：补充

关于overfitting的问题，很大程度上是由于曲线为了更好地拟合training data的数据，而引入了更多的高次项，使得曲线更加“蜿蜒曲折”，反而导致了对testing data的误差更大
我们想要避免overfitting过拟合的问题，就要使得高次项对曲线形状的影响尽可能小。因此我们要在loss function里引入高次项(非线性部分)的衡量标准，也就是将高次项的系数也加权放进loss function中。
这也是我们通常采用的方法，我们不可能一开始就否定高次项而直接只采用低次线性表达式的model，因为有时候真实数据的确是符合高次项非线性曲线的分布的；而如果一开始直接采用高次非线性表达式的model，就很有可能造成overfitting，在曲线偏折的地方与真实数据的误差非常大

在无法确定真实数据分布的情况下，我们要尽可能的改变Loss function的评价标准。

如何判断是bias大还是variance大

如果模型无法fit训练集，那么是bias大，underfitting；如果模型fit训练集但是不fit测试集，那么是variance大，overfitting。
解决underfitting：选取更多的feature，换用更复杂的模型。
解决overfitting：采用更多的数据，正则化（可能会增大bias）。

Adaptive Learning Rates

学习率会衰减

Adagrad

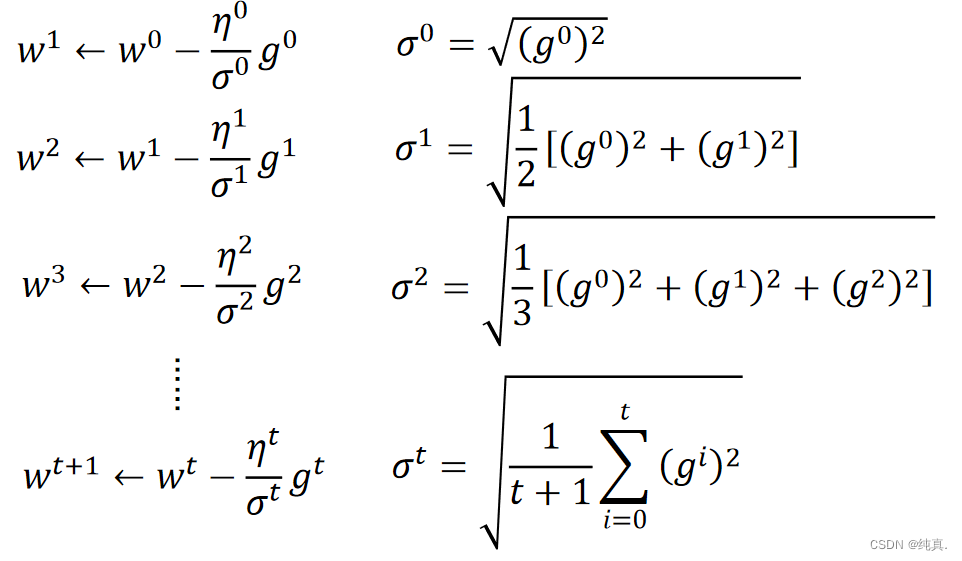
直观原因

分母叠加惯性，造成反差的效果。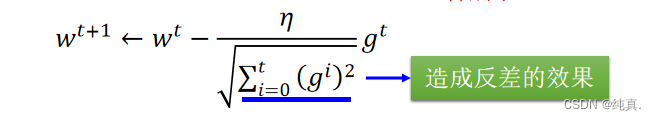
其实这是模拟了一阶导数/二阶导数的形式，最优的结果应该是一阶导数/二阶导数。

随机梯度下降

能够使训练更加的迅速，原先做梯度下降时要算所有loss的求和，而随机梯度下降每次仅取一笔数据算loss就开始更新参数。

特征归一化（feature scaling）

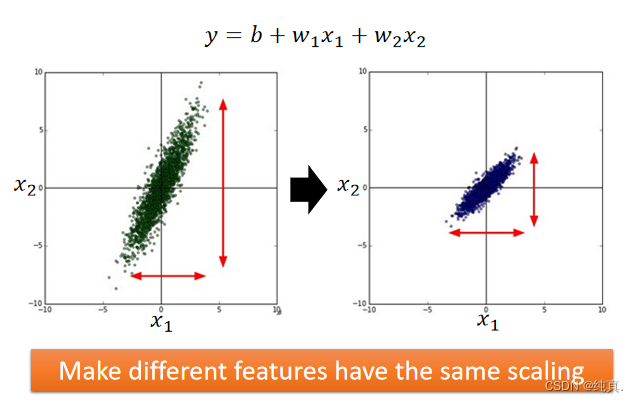将数据减掉均值后除以标准差。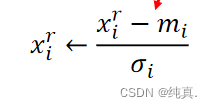

误差来源

误差可能来自变差与方差，即bias以及variance，bias即μ是系统误差，variance为σ2体现的随机误差。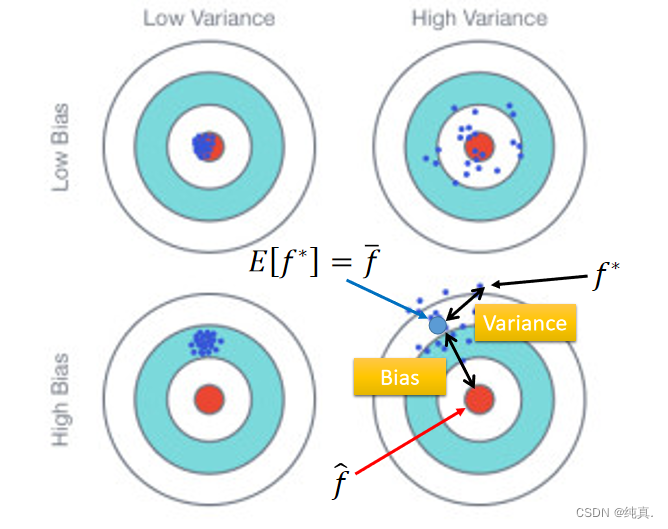
若bias的差距与所想结果差距太大但variance较小，那么将会是一种underfitting的情况，这时候需要改变建立的模型，多加一些特征feature。（无法适应训练集）
若bias的差距较小但variance较大，那么将会是一种overfitting的情况。（过于适应训练集）这时可以选取更多的数据，或进行正则化，但可能会增加bias。

交叉验证

将训练集分成训练集以及验证集再过模型。

分类

概率生成模型（利用贝叶斯公式）

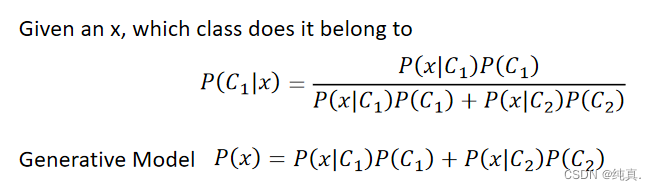
高斯分布

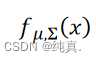利用一组均值和协方差输入x返回一个概率的sample。

极大似然估计

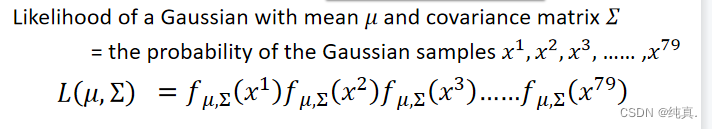把79个点的概率都算出来，而后代入上述式子中，选取一组最大的参数即可。
其实计算出的最终结果就是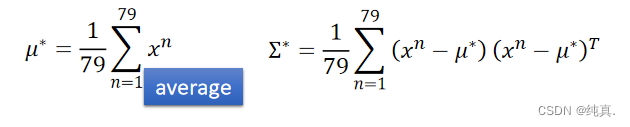均值与协方差。这里对于两个分类而言，最好选择相同的协方差，这样会有更好的效果。可以降低运算复杂度，并且可以避免过拟合问题。

逻辑回归

与生成模型不同的是，这里是直接寻找w和b，而生成模型是生成的w和b。

step1：function set

因为需要将最终的结果归于两类，因此需要使用sigmoid函数进行转换，即我们需要计算的概率P=sigmoid（z）。

Step 2: Goodness of a Function

这里的Loss function选择交叉熵函数，cross entropy。
f（x）表示的是class1，而1-f（x）表示的class2.

Step 3: Find the best function

依旧是梯度下降的方法。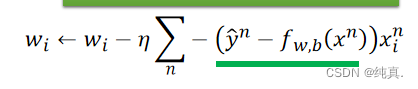

逻辑回归与生成模型

概率生成模型是有预先假定的，比如从高斯分布中得到数据，他们最终得到的w和b是不同的。
当数据很少时可以采用生成模型，且能抵抗噪声。

多分类

one-hot编码

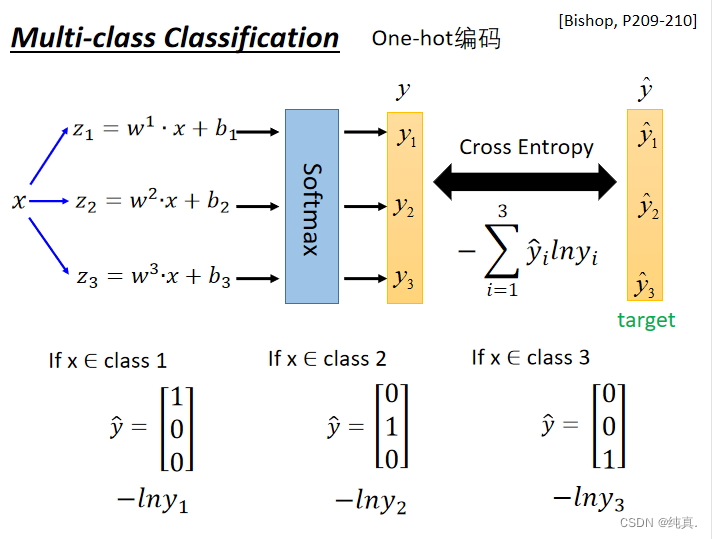
逻辑回归的局限性

有时无法很好的分类，比如如下的情况：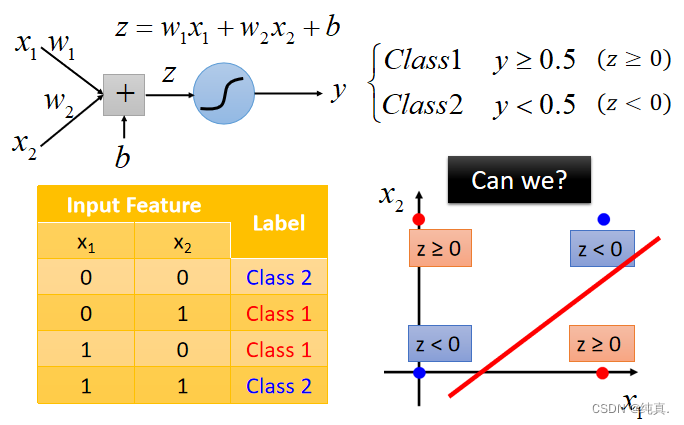
为此需要做Feature transformation，其实就是多过几个sigmoid function。比如用两个sigmoid function来做Feature transformation后再进行分类操作。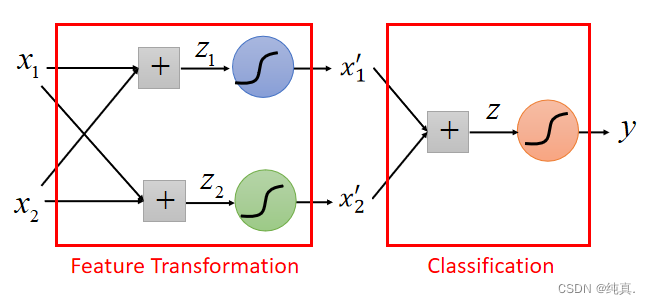

Deep Learning

deep = many hidden layers

全连接前馈型神经网络

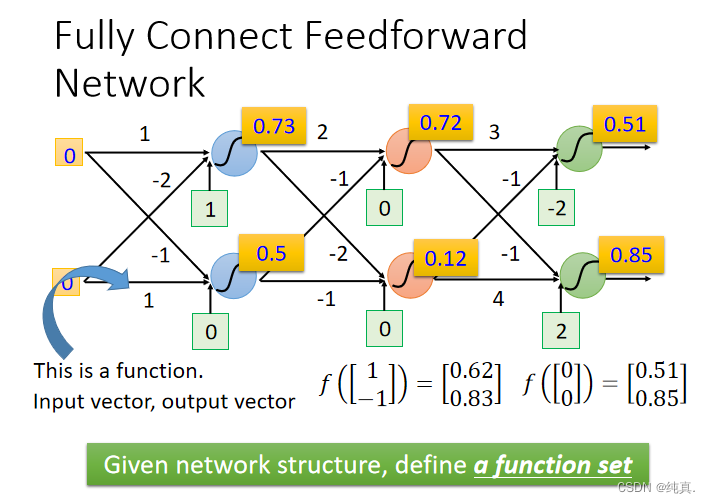
这里的sigmoid function被称为激活函数。
input是一组向量xn，output是一组向量ym，这里m可能会小于n。在计算时可以用矩阵计算，比较方便。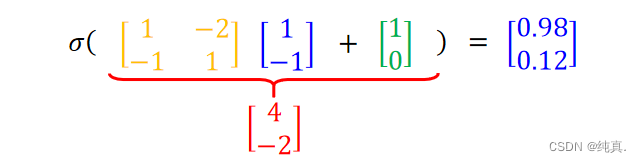

上述是一个数量较少时的网络的实例，总体概括图如下，分为三层，输入层、隐藏层、输出层：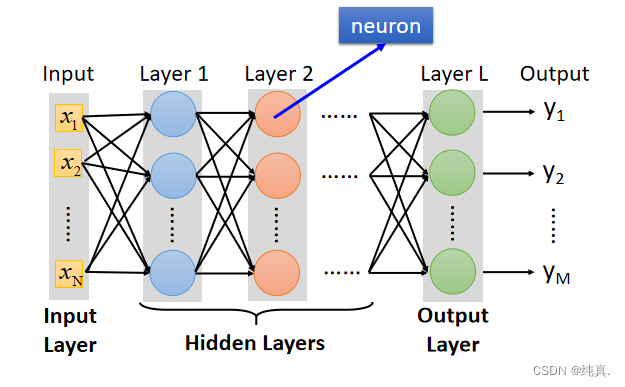
最终的输出层是一个多分类的分类器，使用softmax来实现分类功能。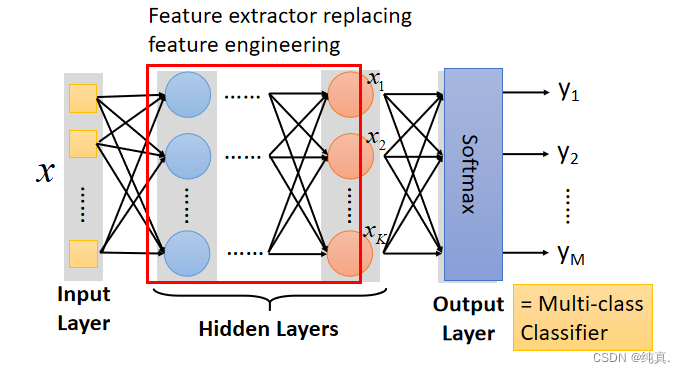

Why deep？

利用梯度下降找best function

这里的Loss function仍然是交叉熵，total loss等于求和的总值。

反向传播实现梯度下降

在实现时使用TensorFlow。
定义：损失函数对参数的梯度通过网络反向流动的过程。

CNN卷积神经网络

比如有某一特征“鸟嘴的形状”，那么不需要将整张图都提供给模型；并且鸟嘴可能出现在一张图片的不同的位置；我们需要降采样（缩小图像）。
卷积convolution：能够解决“不需要整张图”、“一样的模型出现在不同位置的问题”
池化max pooling：可以解决降采样（缩小图像）的问题。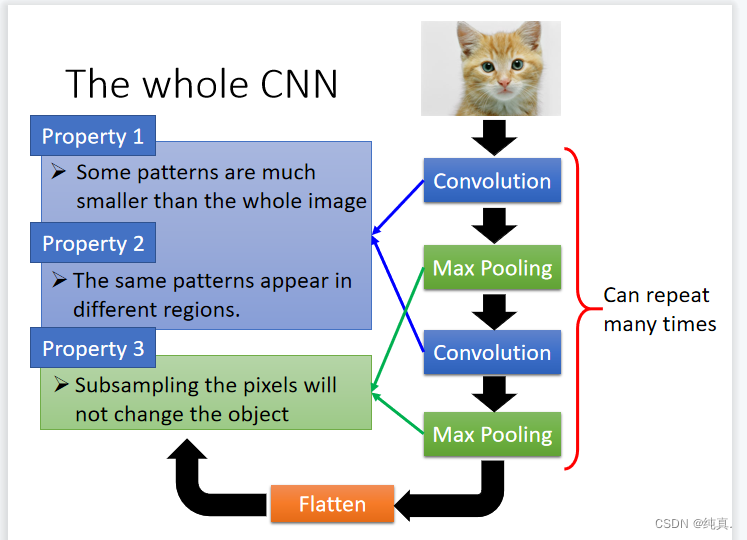

卷积过程

卷积过程需要有一个过滤器filter，每个过滤器表明了一种特征。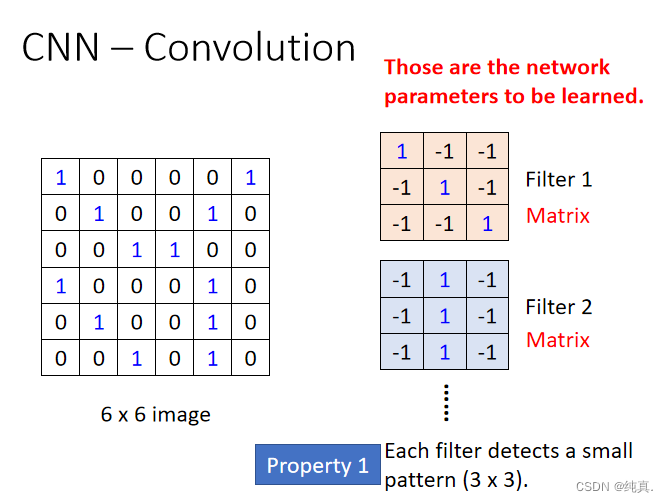
若将过滤器的步长设为1，那么对于上面将会得到一个新的4x4的image。每一个filter都将会得到一个如此的image，称为feature map。
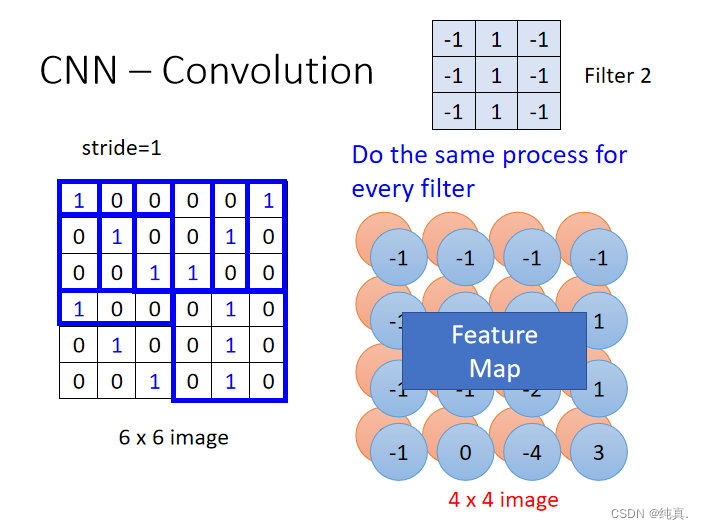过滤器的意义：表明某一种特征在image的各个部分是否存在，比如说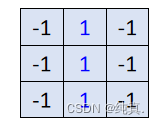代表检测图中有没有竖线。

colorful image

对于一个彩色的image，会有RBG三原色，因此针对每一种颜色需要一个filter，即三重filter。

卷积神经网络对比全连接神经网络

稀疏矩阵：CNN拥有更少的参数
权值共享：CNN拥有共享的权重
相当于简单的全连接

池化Max Pooling

一张image经过卷积Conv后需要经过池化，而后得到new image。池化是解决降采样问题（缩小图片）问题的，因此它是将卷积后的矩阵变得更小的一个方法。

池化过程

比如上述例子中，6x6的image经过卷积得到了4x4的image，而后池化的目标就是将其再压缩为2x2的image，他将4x4的image均分为四份，而后取每一份中的最大值（也可以是平均值）替换此处一个大块。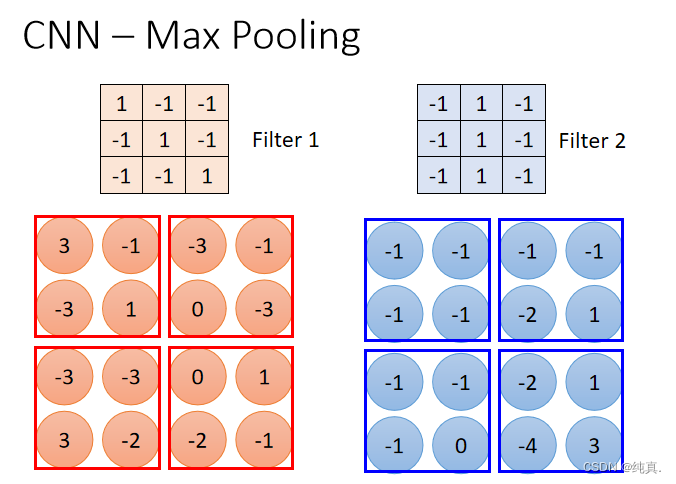
从而可以得到一个2x2的image。
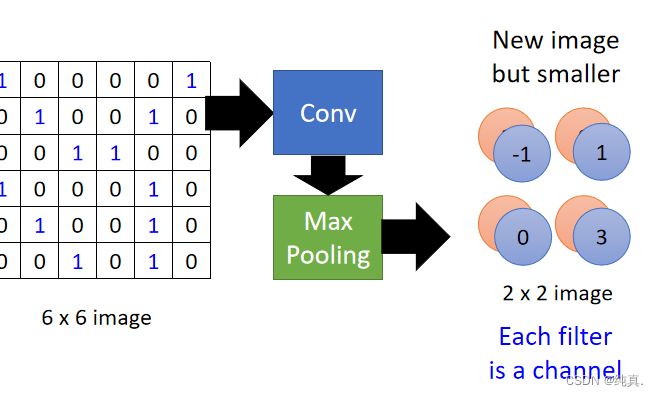the number of channel is the number of filter

Flatten

将池化得到的结果展评，而后进入一个前馈的全连接神经网络进行分类。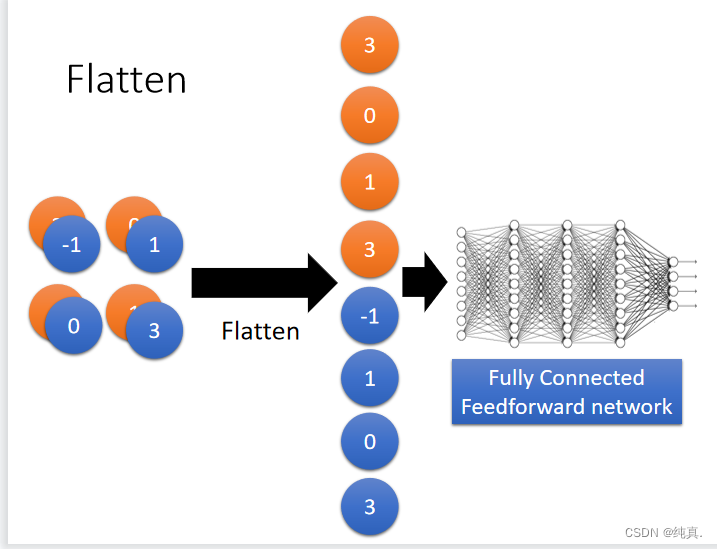

神经网络训练技巧

not well-trained不一定是overfitting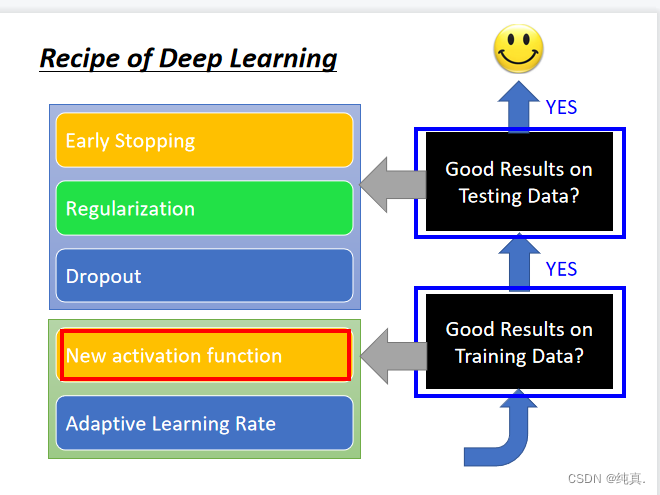

解决训练集上的问题可以采用更换新的激活函数，或者adaptive的学习率。
解决测试集上的结果不好的问题，可以使用正则化，earlystopping以及Dropout的方法。

梯度消失现象

定义

模型前面的梯度小但后面的梯度大的现象。

原因

神经网络中使用的激活函数是sigmoid function，而sigmoid函数将负无穷到正无穷的范围映射到0-1之间，大的输入空间映射到小的映射空间导致靠前层数的梯度小，学习过程慢，输出几乎随机，后面的梯度大，学习过程快，就导致了梯度消失。

解决方案

更改激活函数为ReLu，ReLu可以使得网络变得thinner，因为他在0的地方可以直接省略。使用Maxout方法。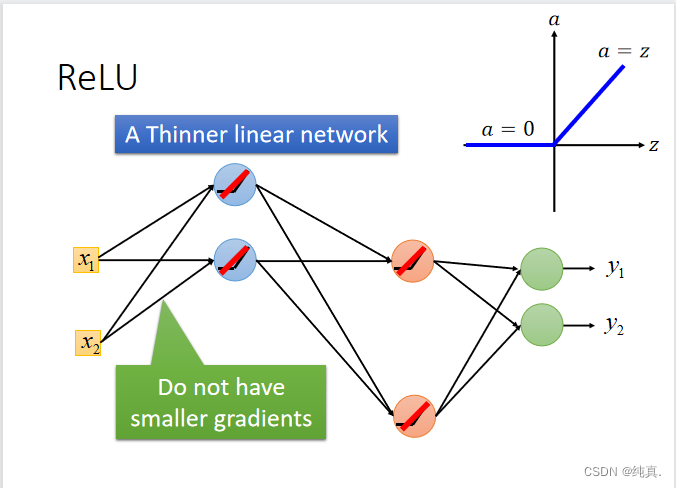
并且ReLu也存在一些变体。
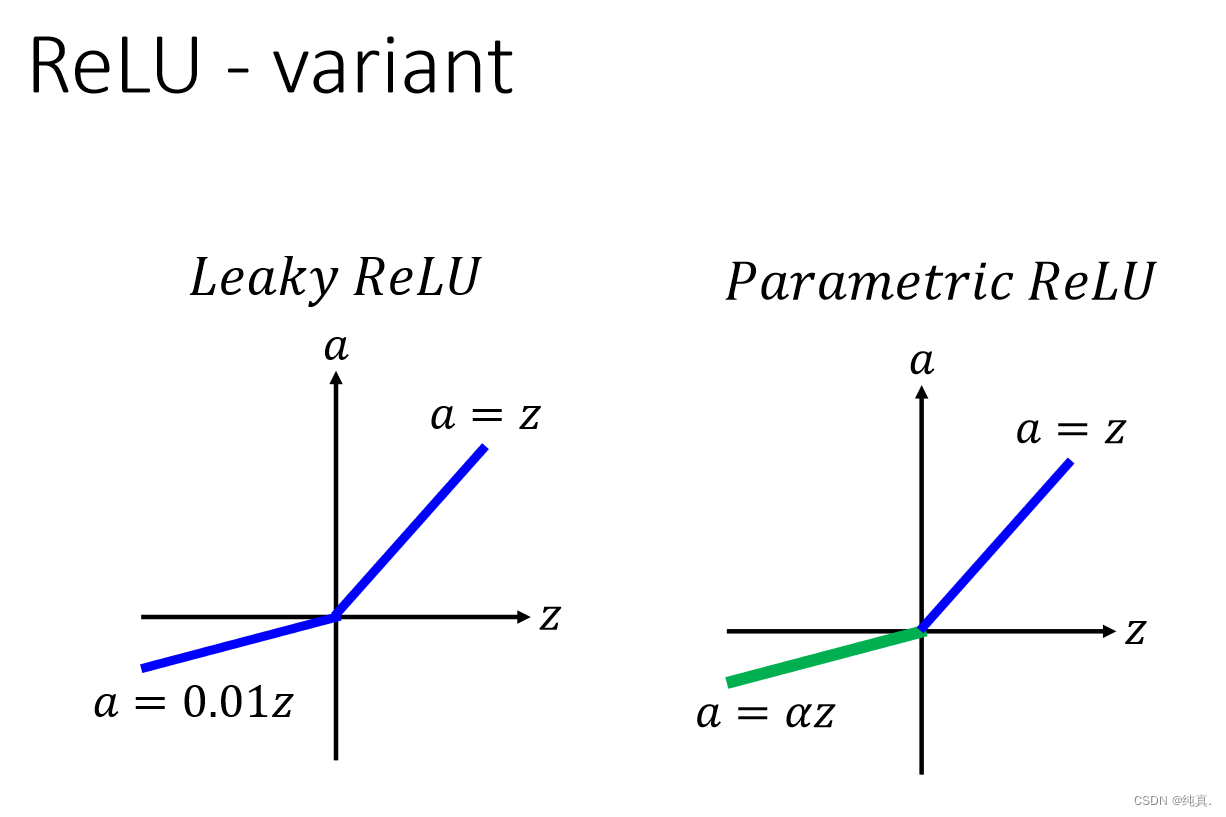ReLu是一种maxout的变式

Maxout

是一种可学习的activation function。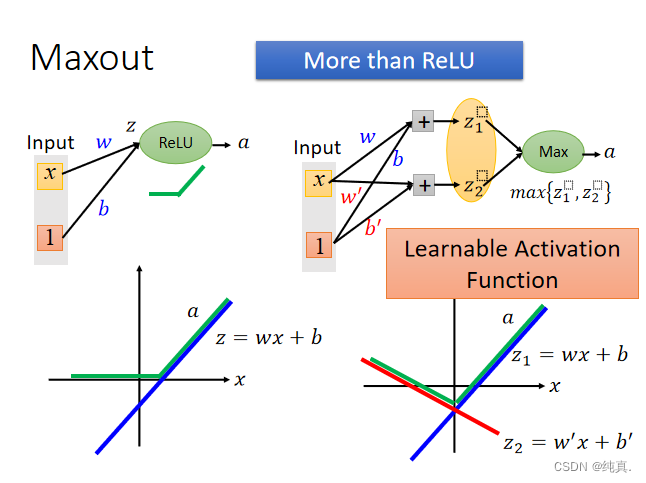
他可以是任何分段的线性函数。在实际训练时知道z是多少，因此不存在max函数的无法求导的问题。

adaptive learning rate

adagrad

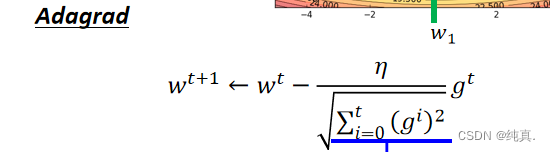adagrad是用一阶导数来估算二阶导数的方法。

RMSProp

在训练神经网络的时候，Error surface往往是十分复杂的，这时候adagrad可能并不是非常的适用。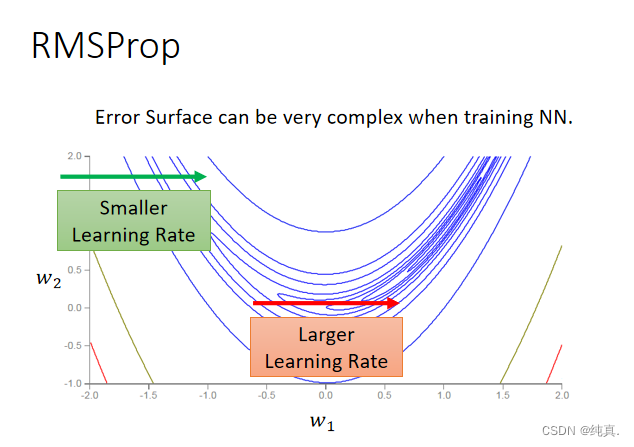以前的梯度的均方根被衰减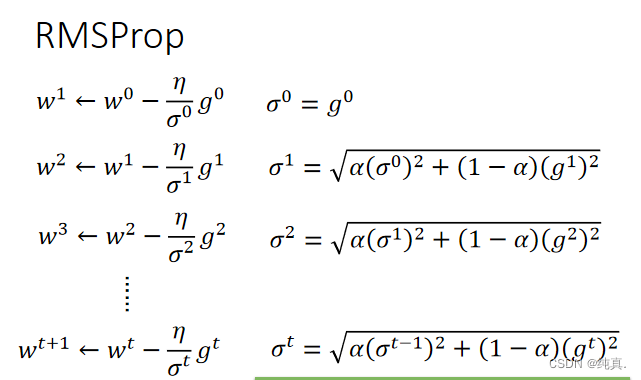

冲量

很难找到最优的网络参数

在训练时，梯度为0的位置可能是local minimal也有可能是鞍部，还有可能就是非常的平缓。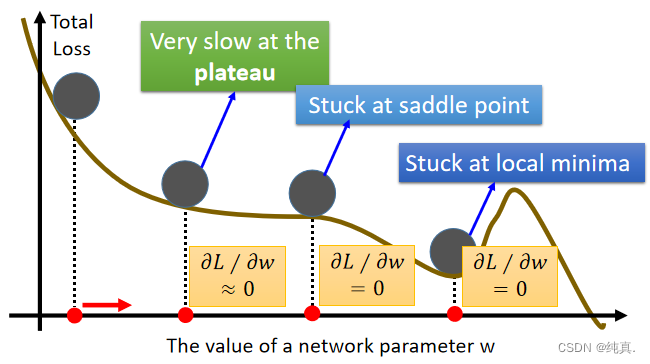

冲量

考虑过去的移动，目前最后一步减去梯度的运动，移动不只是基于梯度，还会基于之前的移动。
Adam就是RMSProp+冲量

Regularization

L2正则化

正则化要做的是改变原先的loss function，在原先的loss function后面再加一个正则化的项。对于L2正则化来说就是所有weight的平方和。
求出他的梯度化简可以发现，其实这里就会是让权值weight更新的慢一些，叫做权值缩减。如此便会让参数离0不要太远。但他的效果往往不如early stopping，因为early stopping是可以人为控制来停止的。

L1正则化

L1正则化采用的是绝对值，将梯度的式子写出来可以发现L1正则化就是在原先loss的基础上不管三七二十一就减掉一个值，如果是正的就减，如果是负的就加。也是让参数变小。

L1正则化与L2正则化的对比

对比式子可以发现，L1正则化是每次都减掉固定的值而L2正则化是按照比例减小参数的值。比如说如果一个数据非常大，那么L2令参数减小的就很快，但L1只能减掉固定的一点；若一个数据非常小，那么L2令参数减小的就很慢，但L1很快。因此最终得到的结果，L1的结果往往是有的离0很近有的离0很远，而L2就是离0都很近。
L1可以使得参数稀疏，而L2可以防止模型overfitting。

Dropout

在训练阶段以p%的概率随机删去神经元，使得网络变得thinner。testing的时候不做dropout，并且在testting的时候所有的weight都要乘1-p%，所以导致两次的时候权值不同，但是其实看最终结果是相近的。
他是一种联合训练的方式。解决了overfitting的问题。

RNN（循环神经网络）

用于序列信息的处理（与时序相关）。RNN使得网络拥有记忆性。

1-of-N encoding

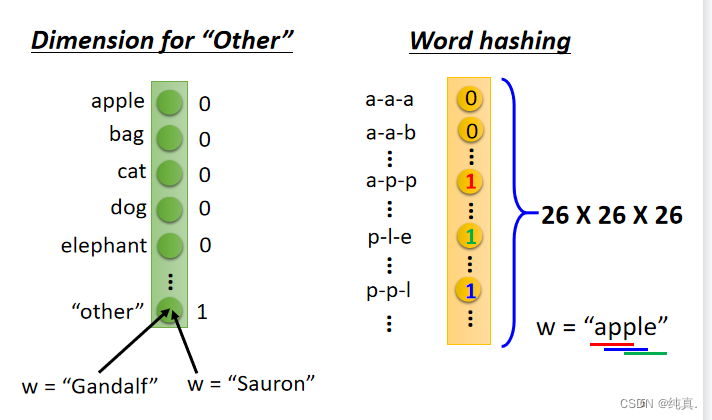就是用向量来标明一组words，因为训练时的输入是一组vector。

简单的RNN

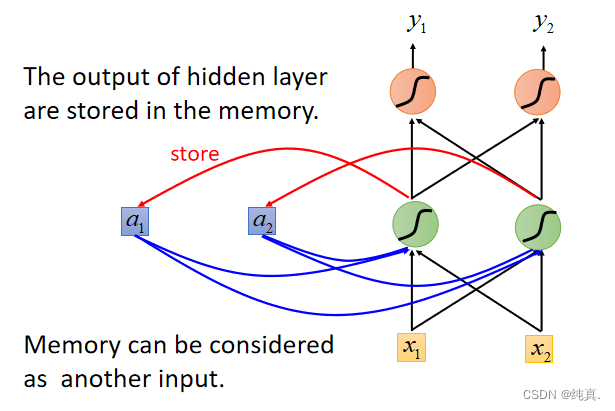这是一个简单的单独的网络，在实际的训练过程中，相同的网络会被重复利用多次。可以用于slot filling信息提取。
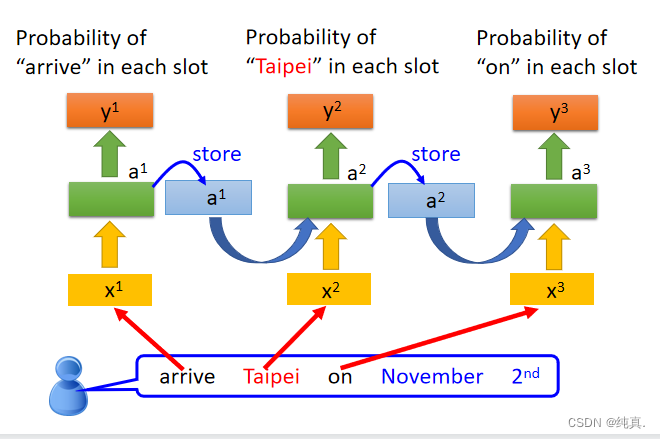由于memory的存在，即便对网络input相同，其output也会是不同的，因为他们的memory中储存的内容不同。
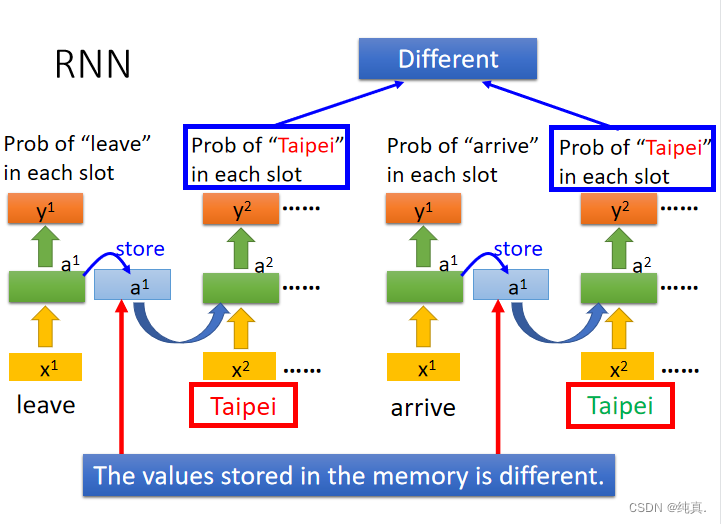因此输入的顺序将会影响结果。

双向RNN

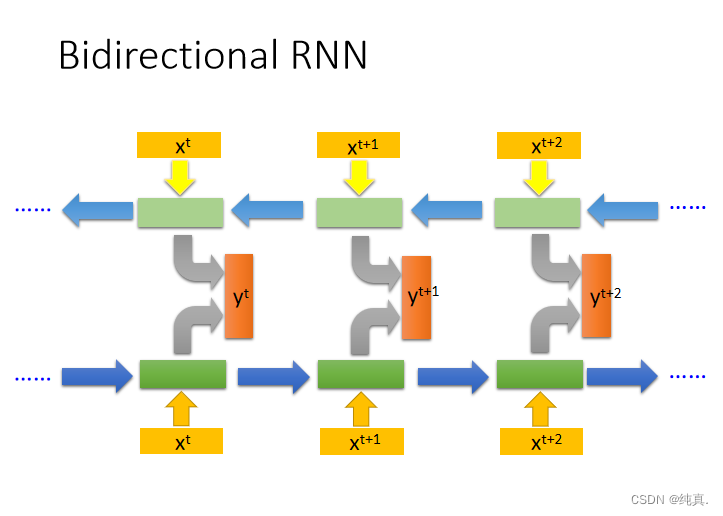从前向后以及从后想前共同进行训练。

LSTM（长短时记忆）

一个LSTM的网络具有四个输入，其中三个是信号来控制的gate。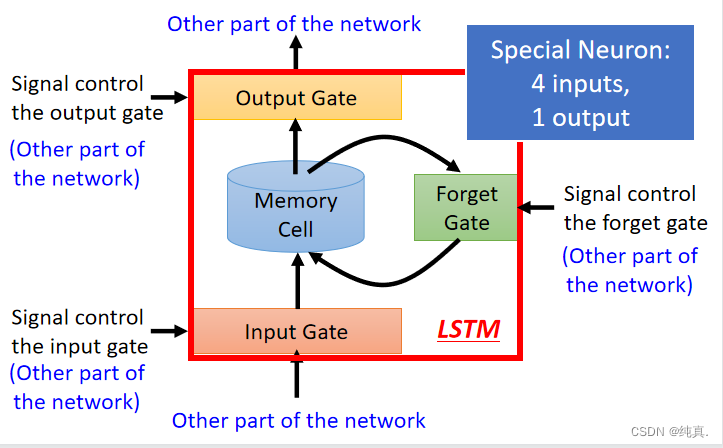
上述是一个简单的概括图，其内部结构如下：
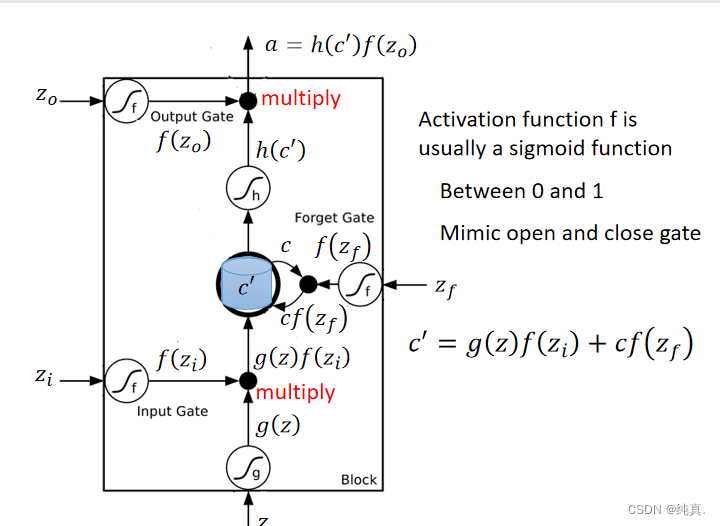可以看到三个信号分别控制输入、输出以及是否遗忘。这里的激活函数选择的是sigmoid function，他的结果非0即1，因此可以用右边表达式来表示memory中的结果c。输出和输入是同理的。
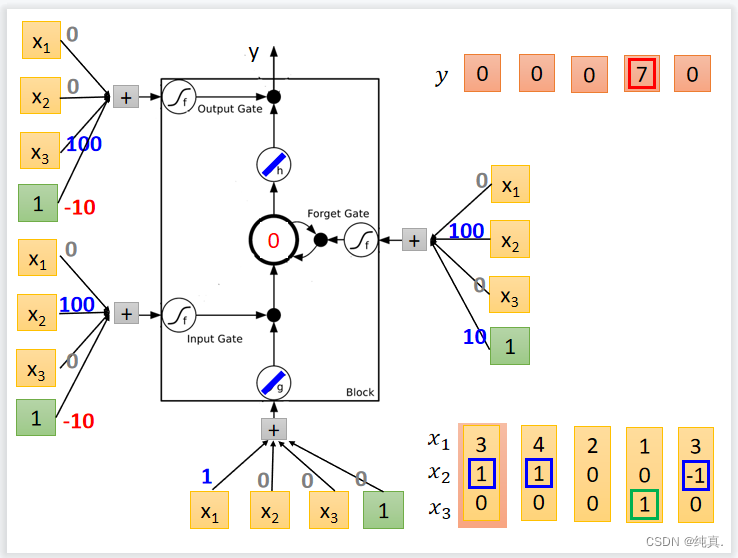这是一个具体的实例。

半监督学习

半监督学习中的生成模型方法和监督学习中的有何异同？

相同点：都通过P（C1|x）来进行分类，都预先假定模型。
不同点：半监督学习需要使用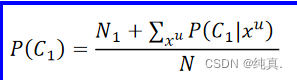更新P（C1），并重新计算P（C1|x），儿子啊监督学习中则不需要。
半监督学习首先从打标数据中获取P（C1|x），在通过无标数据进行更新。
监督学习中生成的模型是一次性计算出来的。

Hard label / Soft label 区别

Hard label是为增加偏见，而soft label只保持原来的概率。

补充

在分类时使用soft label是不会work的，因为他的输入输出没有改变。应该使用hard label，这是一个非黑即白的思想，虽然他只有0.7的概率是，但是就是要让他是1。这是low density separation的思想。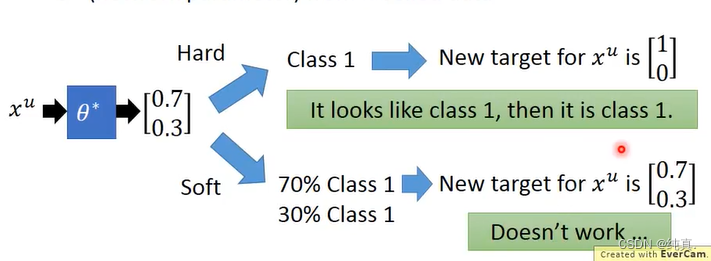
关于low density separation其实就是先用贴标签的数据训练得到f然后再用f给v贴为标签，把贴上标签的从未贴的里面拿出来。

无监督学习

简述聚类中的k-means方法

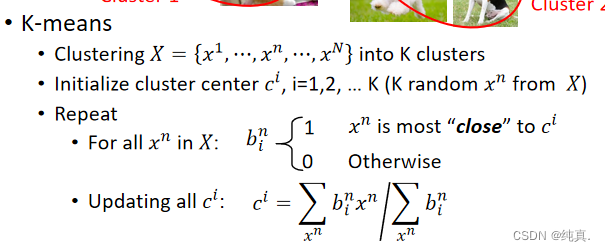更新完聚类中心后，重复第三步。

简述PCA方法以及其实现的最主要目标

PCA，即主成分分析法，将n维特征向量x映射到k维特征向量z上，即z=Wx。其中W是一个正交矩阵。
z1=w1x，取使得z1方差最大的w1；
z2=w2x，取使得z2方差最大的w2，且满足w1w2=0，即正交。

PCA实现的主要目标：降维。

异常检测主要做了什么

给定训练数据X，判断新输入x是否与训练数据相近。若相信，则判断为正常，反之则是异常数据。

期末复习

序章 课程概览

机器学习与人工智能、深度学习三者的关系、区别

人工智能：机器展现出的人类智能
机器学习：计算机利用已有的数据，得出了某种模型，并利用该模型预测未来的一种方法。（实现人工智能的方法）
深度学习：实现机器学习的一种技术
区别：深度学习的计算量更大，而机器学习技术通常更易于使用。

机器学习三步骤

1.定义一个函数集合即模型
2.定义一个损失函数评估模型的好坏
3.选择最好的函数

第一章 回归

解释过拟合和欠拟合现象

过拟合：模型的bias很小，即在训练集上的error很小；但模型的variance很大，即在测试集上的error很大。
欠拟合：模型的bias很大，即当前的模型无法fit训练集上的数据，error较大，在测试集上表现也不会。

解释方差和偏差的概念

偏差（bias）：预测值和真实值之间的差距
方差（variance）：预测值之间的离散程度

正则化的概念和目的

概念：在loss function中加入描述模型复杂程度的正则项，可以防止过拟合并且能够提高模型的泛化性。
目的：1.使得函数能够更加平滑
2.能够防止过拟合并提高模型的泛化性。

简述几种降低过拟合和欠拟合风险的方法

过拟合：训练更多的data；正则化（可能会增大bias）；dropout；降低模型复杂度
欠拟合：重新设计模型，考虑更多的feature；选取更复杂的模型，引入高次项。

第二章 梯度下降

简述梯度下降的过程

这里以一个参数为例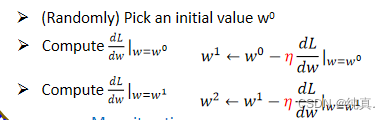

Adagrad方法解决了什么问题，如何做的？

解决的问题：学习率不合适导致迭代次数多以及振荡现象

方法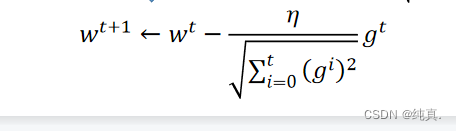：gt就是本次算出的梯度值。

随机梯度下降解决了什么问题，如何做的？

解决的问题：在训练集很大时，训练过慢的情况
做法：在每次更新时仅使用一个样本计算微分值，而不采用所有loss加和的情况。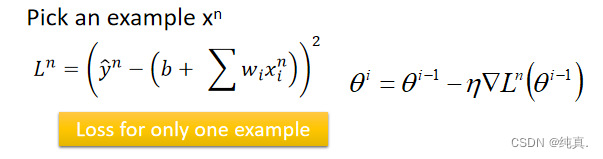

第三章 分类

简述机器学习任务中，回归和分类任务的区别

回归的输出是一个连续数据，分类的输出是一个离散的数据。回归是定量问题，如预测房价，分类是定性问题，如区分男女。

分类和回归任务的模型输出区别

回归的输出是一个连续数据，分类的输出是一个离散的数据。

简述判别模型和生成模型各自的做法以及两种方法的区别

都是计算条件概率分布P（y|x）=σ（wx+b）
判别模型：直接计算出w和b而后采用梯度下降等方法不断更新w和b，作为预测的模型。
生成模型：首先由数据计算出两组的均值以及协方差，而后算出固定的w和b，之后不再变动。以这组参数作为预测的模型。
区别：生成模型有预先假设，输出由高斯分布中得来，判别模型直接计算P（y|x）=σ（wx+b）中的w和b，二者会求出不同的w和b。判别模型受数据量的影响较大，生成模型受数据量的影响较小。

逻辑回归中，若使用平法误差(square error)作为损失函数的表示，可行吗？

不可行。逻辑回归的函数是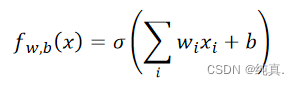若使用平方误差作为loss function，即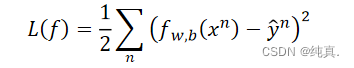此时计算梯度，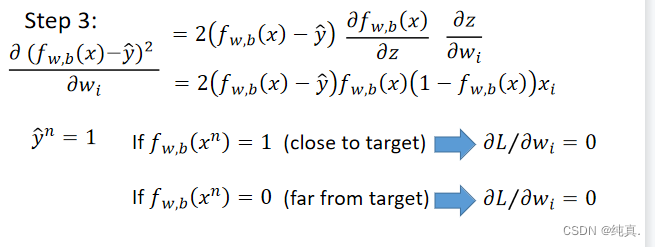

则无法正常进行参数更新。

第四章 深度学习

简述深度学习训练时，反向传播都做了什么

反向传播对所有激活函数的输入z计算损失函数的梯度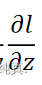
，最终与前向传播计算的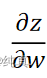相乘，可以得到所有权重关于损失函数的偏导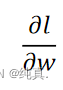

第五章 CNN

简述CNN的卷积层和池化层，各自的实现了什么特性，以及做了什么

卷积层实现的特性：
1.有些模式比整张图小很多，不需要学习整张图
2.一样的模式会在不同的位置出现，需要进行识别。
池化层实现的特性：降采样（缩小图像）
卷积层通过卷积提取输入的不同特征。
池化层对特征进行降维（如取最大值或平均值），压缩参数的数量。

CNN中，卷积操作的本质特性包括稀疏交互和参数共享，具体解释这两种特性及其作用

稀疏交互：
特性：每一个输出神经元仅与前一层特定的部分神经元存在连接关系，称这种特性为稀疏交互。
作用：减少参数个数
参数共享：
特性：在同一个模型的不同模块中使用相同的参数。
作用：减少参数个数，降低存储复杂度。

第六章 神经网络训练技巧

梯度消失产生的原因以及如何解决

原因

神经网络中使用的激活函数是sigmoid function，而sigmoid函数将负无穷到正无穷的范围映射到0-1之间，大的输入空间映射到小的映射空间导致靠前层数的梯度小，学习过程慢，输出几乎随机，后面的梯度大，学习过程快，就导致了梯度消失。

解决方案

将激活函数替换为ReLU，使用Maxout的方法。

冲量(momentum)方法做了什么以及解决了什么问题

冲量方法解决了梯度接近于0导致学习缓慢、鞍点和局部最小值的问题。考虑过去的移动量。

dropout方法做了什么以及解决了什么问题

dropout方法解决了过拟合问题，以p%的概率随机删掉神经元。

L1&L2 正则化

L1正则化可以使得参数稀疏化，L2正则化可以防止模型过拟合。

第七章 RNN

相比CNN与传统DNN，RNN是为了解决什么问题？如何解决的？

RNN是为了解决序列信息处理，CNN和传统的DNN无法解决与时序相关的问题，比如他们不会知道句子的上一个单词是什么，RNN使得网络有记忆，会将前面的信息或后面的信息进行存储并应用于当前的输出计算中。

长短时记忆网络LSTM四个主要的模块及其各自作用

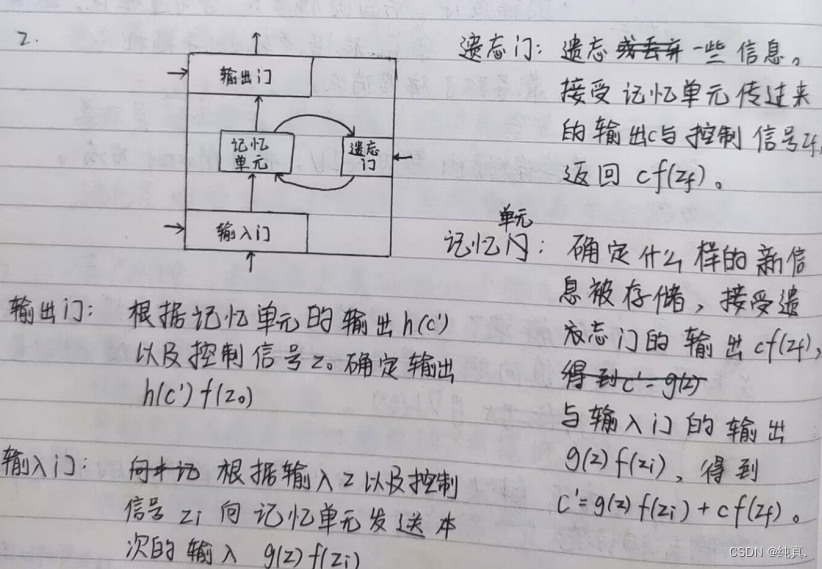
RNN训练中为什么会出现梯度爆炸现象

由于预测的误差是沿着神经网络的每一层传播的，因此当雅克比矩阵的最大特征值大于1时，随着离输出越来越远，每层的梯度大小会呈指数增长，导致梯度爆炸。

第八章 半监督学习

半监督学习中的生成模型方法和监督学习中的有何异同？

相同点：都通过P（C1|x）来进行分类，都预先假定模型。
不同点：半监督学习需要使用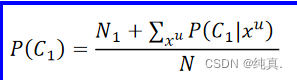更新P（C1），并重新计算P（C1|x），而在监督学习中则不需要。
半监督学习首先从打标数据中获取P（C1|x），在通过无标数据进行更新。
监督学习中生成的模型是一次性计算出来的。

Hard label / Soft label 区别

Hard label是为增加偏见，而soft label只保持原来的概率。

第九章 无监督学习

简述聚类中的k-means方法

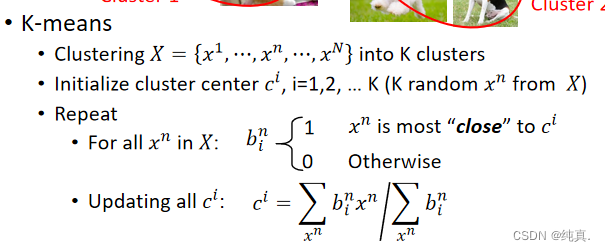更新完聚类中心后，重复第三步。

简述PCA方法以及其实现的最主要目标

PCA，即主成分分析法，将n维特征向量x映射到k维特征向量z上，即z=Wx。其中W是一个正交矩阵。
z1=w1x，取使得z1方差最大的w1；
z2=w2x，取使得z2方差最大的w2，且满足w1w2=0，即正交。

PCA实现的主要目标：降维。

异常检测主要做了什么

给定训练数据X，判断新输入x是否与训练数据相近。若相近，则判断为正常，反之则是异常数据。