**作者|**PINN山里娃,作者主页
**研究方向|**物理信息驱动深度学习 不确定性 人工智能 偏微分方程 极限学习机
该作者聚焦深度学习模型与物理信息结合前沿研究,提供了一系列AI for science研究进展报告及代码实现,旨在实现物理信息驱动深度学习方法入门到精通。
内嵌物理知识神经网络(PINN)入门及相关论文
深度学习求解微分方程系列一:PINN求解框架(Poisson 1d)
深度学习求解微分方程系列二:PINN求解burger方程正问题
深度学习求解微分方程系列三:PINN求解burger方程逆问题
深度学习求解微分方程系列四:基于自适应激活函数PINN求解burger方程逆问题
深度学习求解微分方程系列五:PINN求解Navier-Stokes方程正逆问题
一种基于物理信息极限学习机的PDE求解方法
近年来,物理信息驱动的深度学习方法用于科学计算问题受到了越来越多的关注,其中,physic informed neural network(PINN)在求解微分方程(PDE)正逆问题上展现出巨大的优势,但是并不适用于某些需要实时响应的应用。由此,下面将介绍一种基于物理信息极限学习机的PDE求解方法,用于线性微分方程的快速求解,能实现近实时高精度求解(秒级求解)。首先介绍PINN及极限学习机基本方法,其次介绍基于物理信息的极限学习方法,随后介绍求解问题与背景,最后展示基于Pytorch实现的算例结果。
优点:基于物理信息极限学习机的PDE求解方法能够毫秒级求解线性微分方程,而且该方法为无网格方法,可用于复杂形状系统。
1.问题背景
线性微分方程还是理论联系实践的重要渠道之一,在物理、工程、力学、天文学、生物学、医学、经济学等诸多领域都有重要作用。如电子计算机与无线电装置的计算问题可归为微分方程求解;弹道计算与飞机飞行中的稳定性研究可归为线性微分方程的求解。对于线性PDE可描述为
L
u
=
f
λ
(
x
,
y
)
,
(
x
,
y
)
∈
Ω
B
[
u
(
x
,
y
)
]
=
b
(
x
,
y
)
,
(
x
,
y
)
∈
∂
Ω
\begin{aligned} &L u=f_\lambda(x, y),(x, y) \in \Omega \\ &\mathcal{B}[u(x, y)]=b(x, y),(x, y) \in \partial \Omega \end{aligned}
Lu=fλ(x,y),(x,y)∈ΩB[u(x,y)]=b(x,y),(x,y)∈∂Ω
式中:
L
L
L 为线性微分算子,
B
B
B 为边界或初值条件,
f
λ
(
x
,
y
)
f_{\lambda}(x,y)
fλ(x,y) 为系统源项,
λ
\lambda
λ为物理参数,
u
u
u为物理系统的解。
2.PINN及极限学习机简介
神经网络作为一种强大的信息处理工具在计算机视觉、生物医学、 油气工程领域得到广泛应用, 引发多领域技术变革。深度学习网络具有非常强的学习能力, 不仅能发现物理规律, 还能求解偏微分方程。近年来,基于深度学习的偏微分方程求解已是研究新热点。PINN是一种科学机器在传统数值领域的应用方法,能够用于解决与PDE相关的各种问题,包括方程求解、参数反演、模型发现、控制与优化等。随着神经网络的发展,极限学习机(ELM)由于其好的泛化性能以及极快的学习能力,在图像分类和回归问题上得到了非常大的。
2.1PINN方法求解逆问题
PINN的主要思想如图1,先构建一个输出结果为
u
^
\hat{u}
u^的神经网络,将其作为PDE解的代理模型,将PDE信息作为约束,编码到神经网络损失函数中进行训练。损失函数主要包括4部分:偏微分结构损失(PDE loss),边值条件损失(BC loss)、初值条件损失(IC loss)以及真实数据条件损失(Data loss)。

图1:PINN示意图
特别的,考虑下面这个的PDE问题,其中PDE的解
u
(
x
)
u(x)
u(x)在
Ω
⊂
R
d
\Omega \subset \mathbb{R}^{d}
Ω⊂Rd定义,其中
x
=
(
x
1
,
…
,
x
d
)
\mathbf{x}=\left(x_{1}, \ldots, x_{d}\right)
x=(x1,…,xd):
f
(
x
;
∂
u
∂
x
1
,
…
,
∂
u
∂
x
d
;
∂
2
u
∂
x
1
∂
x
1
,
…
,
∂
2
u
∂
x
1
∂
x
d
)
=
0
,
x
∈
Ω
f\left(\mathbf{x} ; \frac{\partial u}{\partial x_{1}}, \ldots, \frac{\partial u}{\partial x_{d}} ; \frac{\partial^{2} u}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} u}{\partial x_{1} \partial x_{d}} \right)=0, \quad \mathbf{x} \in \Omega
f(x;∂x1∂u,…,∂xd∂u;∂x1∂x1∂2u,…,∂x1∂xd∂2u)=0,x∈Ω
同时,满足下面的边界
B
(
u
,
x
)
=
0
on
∂
Ω
\mathcal{B}(u, \mathbf{x})=0 \quad \text { on } \quad \partial \Omega
B(u,x)=0 on ∂Ω
PINN求解过程主要包括:
- 第一步,首先定义D层全连接层的神经网络模型: N Θ : = L D ∘ σ ∘ L D − 1 ∘ σ ∘ ⋯ ∘ σ ∘ L 1 N_{\Theta}:=L_D \circ \sigma \circ L_{D-1} \circ \sigma \circ \cdots \circ \sigma \circ L_1 NΘ:=LD∘σ∘LD−1∘σ∘⋯∘σ∘L1 式中: L 1 ( x ) : = W 1 x + b 1 , W 1 ∈ R d 1 × d , b 1 ∈ R d 1 L i ( x ) : = W i x + b i , W i ∈ R d i × d i − 1 , b i ∈ R d i , ∀ i = 2 , 3 , ⋯ D − 1 , L D ( x ) : = W D x + b D , W D ∈ R N × d D − 1 , b D ∈ R N . \begin{aligned} L_1(x) &:=W_1 x+b_1, \quad W_1 \in \mathbb{R}^{d_1 \times d}, b_1 \in \mathbb{R}^{d_1} \ L_i(x) &:=W_i x+b_i, \quad W_i \in \mathbb{R}^{d_i \times d_{i-1}}, b_i \in \mathbb{R}^{d_i}, \forall i=2,3, \cdots D-1, \ L_D(x) &:=W_D x+b_D, \quad W_D \in \mathbb{R}^{N \times d_{D-1}}, b_D \in \mathbb{R}^N . \end{aligned} L1(x)Li(x)LD(x):=W1x+b1,W1∈Rd1×d,b1∈Rd1:=Wix+bi,Wi∈Rdi×di−1,bi∈Rdi,∀i=2,3,⋯D−1,:=WDx+bD,WD∈RN×dD−1,bD∈RN. 以及 σ \sigma σ 为激活函数, W W W 和 b b b 为权重和偏差参数。
- 第二步,为了衡量神经网络 u ^ \hat{u} u^和约束之间的差异,考虑损失函数定义: L ( θ ) = w f L P D E ( θ ; T f ) + w i L I C ( θ ; T i ) + w b L B C ( θ , ; T b ) + w d L D a t a ( θ , ; T d a t a ) \mathcal{L}\left(\boldsymbol{\theta}\right)=w_{f} \mathcal{L}{PDE}\left(\boldsymbol{\theta}; \mathcal{T}{f}\right)+w_{i} \mathcal{L}{IC}\left(\boldsymbol{\theta} ; \mathcal{T}{i}\right)+w_{b} \mathcal{L}{BC}\left(\boldsymbol{\theta},; \mathcal{T}{b}\right)+w_{d} \mathcal{L}{Data}\left(\boldsymbol{\theta},; \mathcal{T}{data}\right) L(θ)=wfLPDE(θ;Tf)+wiLIC(θ;Ti)+wbLBC(θ,;Tb)+wdLData(θ,;Tdata) 式中: L P D E ( θ ; T f ) = 1 ∣ T f ∣ ∑ x ∈ T f ∥ f ( x ; ∂ u ^ ∂ x 1 , … , ∂ u ^ ∂ x d ; ∂ 2 u ^ ∂ x 1 ∂ x 1 , … , ∂ 2 u ^ ∂ x 1 ∂ x d ) ∥ 2 2 L I C ( θ ; T i ) = 1 ∣ T i ∣ ∑ x ∈ T i ∥ u ^ ( x ) − u ( x ) ∥ 2 2 L B C ( θ ; T b ) = 1 ∣ T b ∣ ∑ x ∈ T b ∥ B ( u ^ , x ) ∥ 2 2 L D a t a ( θ ; T d a t a ) = 1 ∣ T d a t a ∣ ∑ x ∈ T d a t a ∥ u ^ ( x ) − u ( x ) ∥ 2 2 \begin{aligned} \mathcal{L}{PDE}\left(\boldsymbol{\theta} ; \mathcal{T}{f}\right) &=\frac{1}{\left|\mathcal{T}{f}\right|} \sum{\mathbf{x} \in \mathcal{T}{f}}\left|f\left(\mathbf{x} ; \frac{\partial \hat{u}}{\partial x{1}}, \ldots, \frac{\partial \hat{u}}{\partial x_{d}} ; \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{1}}, \ldots, \frac{\partial^{2} \hat{u}}{\partial x_{1} \partial x_{d}} \right)\right|{2}^{2} \ \mathcal{L}{IC}\left(\boldsymbol{\theta}; \mathcal{T}{i}\right) &=\frac{1}{\left|\mathcal{T}{i}\right|} \sum_{\mathbf{x} \in \mathcal{T}{i}}|\hat{u}(\mathbf{x})-u(\mathbf{x})|{2}^{2} \ \mathcal{L}{BC}\left(\boldsymbol{\theta}; \mathcal{T}{b}\right) &=\frac{1}{\left|\mathcal{T}{b}\right|} \sum{\mathbf{x} \in \mathcal{T}{b}}|\mathcal{B}(\hat{u}, \mathbf{x})|{2}^{2}\ \mathcal{L}{Data}\left(\boldsymbol{\theta}; \mathcal{T}{data}\right) &=\frac{1}{\left|\mathcal{T}{data}\right|} \sum{\mathbf{x} \in \mathcal{T}{data}}|\hat{u}(\mathbf{x})-u(\mathbf{x})|{2}^{2} \end{aligned} LPDE(θ;Tf)LIC(θ;Ti)LBC(θ;Tb)LData(θ;Tdata)=∣Tf∣1x∈Tf∑∥∥∥∥f(x;∂x1∂u^,…,∂xd∂u^;∂x1∂x1∂2u^,…,∂x1∂xd∂2u^)∥∥∥∥22=∣Ti∣1x∈Ti∑∥u^(x)−u(x)∥22=∣Tb∣1x∈Tb∑∥B(u^,x)∥22=∣Tdata∣1x∈Tdata∑∥u^(x)−u(x)∥22 w f w_{f} wf, w i w_{i} wi、 w b w_{b} wb和 w d w_{d} wd是权重。 T f \mathcal{T}{f} Tf, T i \mathcal{T}{i} Ti、 T b \mathcal{T}{b} Tb和 T d a t a \mathcal{T}{data} Tdata表示来自PDE,初值、边值以及真值的residual points。这里的 T f ⊂ Ω \mathcal{T}_{f} \subset \Omega Tf⊂Ω是一组预定义的点来衡量神经网络输出 u ^ \hat{u} u^与PDE的匹配程度。
- 最后,利用梯度优化算法最小化损失函数,直到找到满足预测精度的网络参数 KaTeX parse error: Undefined control sequence: \theat at position 1: \̲t̲h̲e̲a̲t̲^{*}。
值得注意的是,对于逆问题,即方程中的某些参数未知。若只知道PDE方程及边界条件,PDE参数未知,该逆问题为非定问题,所以必须要知道其他信息,如部分观测点
u
u
u 的值。在这种情况下,PINN做法可将方程中的参数作为未知变量,加到训练器中进行优化,损失函数包括Data loss。
2.2 ELM方法求解
考虑如图2的ELM,它由 n 个神经元的单层前馈神经网络构成,假设输入为
x
=
(
x
1
,
⋯
,
x
j
)
T
\mathbf{x}=(x_{1}, \cdots,x_{j})^{T}
x=(x1,⋯,xj)T,输出为一个神经元
y
y
y ,ELM主要思想是,输入层权值和偏差是预先设定的随机值,并且在整个训练过程中都是固定的,通过训练学习得到输出层权值。

图2:极限学习机示意图
ELM求解方法
首先,确定前馈神经网络结构,初始化输入权重和偏差(初始化后固定)、输出层权重(待求解)。输入输出的映射可以表示为:
G
(
x
)
ν
=
y
\mathbf{G} (\mathbf{x}) \nu=\mathbf{y}
G(x)ν=y
式中:
G
=
[
g
(
x
⃗
1
)
,
g
(
x
⃗
2
)
,
…
,
g
(
x
⃗
j
)
]
T
\boldsymbol{G}=\left[g\left(\vec{x}_1\right), g\left(\vec{x}_2\right), \ldots, g\left(\vec{x}_j\right)\right]^T
G=[g(x1),g(x2),…,g(xj)]T,
G
(
x
k
)
=
[
φ
(
a
j
1
T
x
k
+
b
1
)
,
φ
(
a
j
2
T
x
k
+
b
2
)
,
…
,
φ
(
a
j
n
T
x
k
+
b
n
)
]
{G}\left({x}_k\right)=\left[\varphi\left({a}_{j1}^T {x}_k+b_1\right), \varphi\left({a}_{j2}^T {x}_k+b_2\right), \ldots, \varphi\left({a}_{jn}^T {x}_k+b_{n}\right)\right]
G(xk)=[φ(aj1Txk+b1),φ(aj2Txk+b2),…,φ(ajnTxk+bn)]
然后通过求解最小二乘法方法求得输出层权重
ν
=
pin
v
(
G
)
x
\nu=\operatorname{pin} v(\boldsymbol{G}) \mathbf{x}
ν=pinv(G)x
3.基于物理信息的极限学习机方法
基于物理信息极限学习机方法作为PINN的快速版本,在求解偏微分方程方面受到了广泛关注。其关键特征是用随机值固定输入层权值,并对输出层权值使用Moore-Penrose广义逆求解。
步骤:
- 首先,确定神经网络结构,单层神经网络( n n n个神经元),随机初始化输入层权值和偏差并固定,随机初始化输出层权值。假设 χ = [ x , y , 1 ] T , α = [ α 1 , α 2 , ⋯ , α n ] T , β = [ β 1 , β 2 , ⋯ , β n ] T , γ = [ γ 1 , γ 2 , ⋯ , γ n ] T \chi=[x, y, 1]^T, \boldsymbol{\alpha}=\left[\alpha_1, \alpha_2, \cdots, \alpha_n\right]^T, \boldsymbol{\beta}=\left[\beta_1, \beta_2, \cdots, \beta_n\right]^T,\gamma=\left[\gamma_1, \gamma_2, \cdots, \gamma_n\right]^T χ=[x,y,1]T,α=[α1,α2,⋯,αn]T,β=[β1,β2,⋯,βn]T,γ=[γ1,γ2,⋯,γn]T 式中: α , β \alpha, \beta α,β和 γ \gamma γ为输出层参数,通过随机初始化后固定。网络中使用非线性激活函数 φ = tanh \varphi=\tanh φ=tanh,输出层参数为 ω = [ ω 1 , ω 2 , ⋯ , ω n ] T \boldsymbol{\omega}=\left[\omega_1, \omega_2, \cdots, \omega_n\right]^T ω=[ω1,ω2,⋯,ωn]T,第 k k k个神经元的输出可表示为 φ ( z k ) \varphi\left(z_k\right) φ(zk), z k = [ α k , β k , γ k ] χ z_k=\left[\alpha_k, \beta_k, \gamma_k\right] \chi zk=[αk,βk,γk]χ,神经网络输出可表示为 u ^ ( χ ) = φ ( z ) ω \hat{u}(\chi)=\varphi(z) \omega u^(χ)=φ(z)ω
- 其次,将物理信息编码到极限学习网络中,由于极限学习机网络的特殊性,线性PDE方程和边界条件可描述为 ξ f = L φ ( z ) ω − f λ ( x , y ) = 0 ξ b = B [ φ ( z ) ω ] − b ( x , y ) = 0 \begin{aligned} &\boldsymbol{\xi}_f=L \varphi(\boldsymbol{z}) \boldsymbol{\omega}-f_\lambda(x, y)=0 \ &\boldsymbol{\xi}_b=\mathcal{B}[\varphi(\boldsymbol{z}) \boldsymbol{\omega}]-b(x, y)=0 \end{aligned} ξf=Lφ(z)ω−fλ(x,y)=0ξb=B[φ(z)ω]−b(x,y)=0 通过上式,可得到 H ω = Y \mathbf{H} \boldsymbol{\omega}=\mathbf{Y} Hω=Y 式中: H H \mathbf{H} \mathbf{H} HH和 Y \mathbf{Y} Y是由 L L L和 B \mathcal{B} B所确定的matrix。 然后,求解网络权重参数,利用Moore-Penrose广义逆求解可得 w ∗ = pin v ( H ) Y \boldsymbol{w}^{*}=\operatorname{pin} v(\boldsymbol{H}) \mathbf{Y} w∗=pinv(H)Y
- 最后,得到PDE的解 u ^ ( χ ) = φ ( z ) w ∗ \hat{u}(\chi)=\varphi(z) \boldsymbol{w}^{*} u^(χ)=φ(z)w∗
4.算例展示
4.1 2D Poisson Equation
u
x
x
+
u
y
y
=
(
16
x
2
+
64
y
2
−
12
)
e
−
(
2
x
2
+
4
y
2
)
,
(
x
,
y
)
∈
Ω
u_{x x}+u_{y y}=\left(16 x^2+64 y^2-12\right) e^{-\left(2 x^2+4 y^2\right)},(x, y) \in \Omega
uxx+uyy=(16x2+64y2−12)e−(2x2+4y2),(x,y)∈Ω
式中:
Ω
=
{
(
x
,
y
)
∣
x
=
0.55
ρ
(
θ
)
cos
(
θ
)
,
y
=
0.75
ρ
(
θ
)
sin
(
θ
)
}
\Omega=\{(x, y) \mid x=0.55 \rho(\theta) \cos (\theta), y=0.75 \rho(\theta) \sin (\theta)\}
Ω={(x,y)∣x=0.55ρ(θ)cos(θ),y=0.75ρ(θ)sin(θ)},
ρ
(
θ
)
=
1
+
cos
(
θ
)
sin
(
4
θ
)
,
0
≤
θ
≤
2
π
\rho(\theta)=1+\cos (\theta) \sin (4 \theta), 0 \leq \theta \leq 2 \pi
ρ(θ)=1+cos(θ)sin(4θ),0≤θ≤2π
方程真实解为:
u
=
1
2
+
e
−
(
2
x
2
+
4
y
2
)
u=\frac{1}{2}+e^{-\left(2 x^2+4 y^2\right)}
u=21+e−(2x2+4y2)
4.2 结果
基于物理信息的极限学习机预测结果如图3所示,可看出,预测结果能方程好接近真解,同时计算时间为0.85s。
图3:基于物理信息的极限学习机预测
PINN预测结果如图4所示,PINN计算时间为144s,同时预测精度比基于物理信息的极限学习机差两个数量级。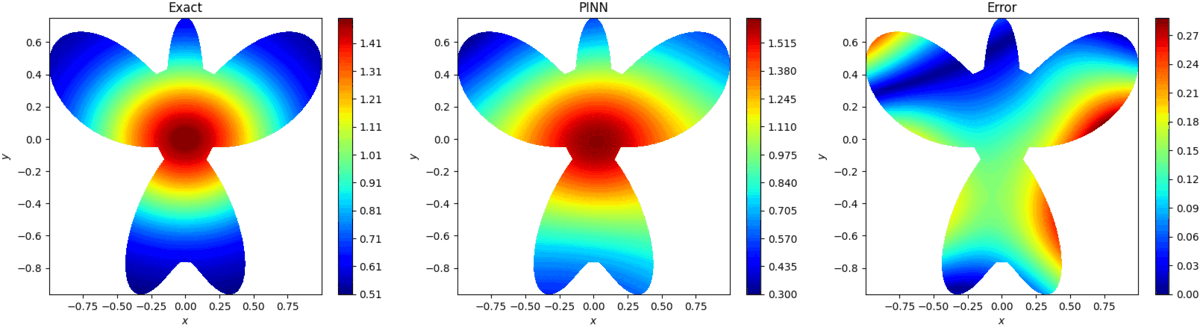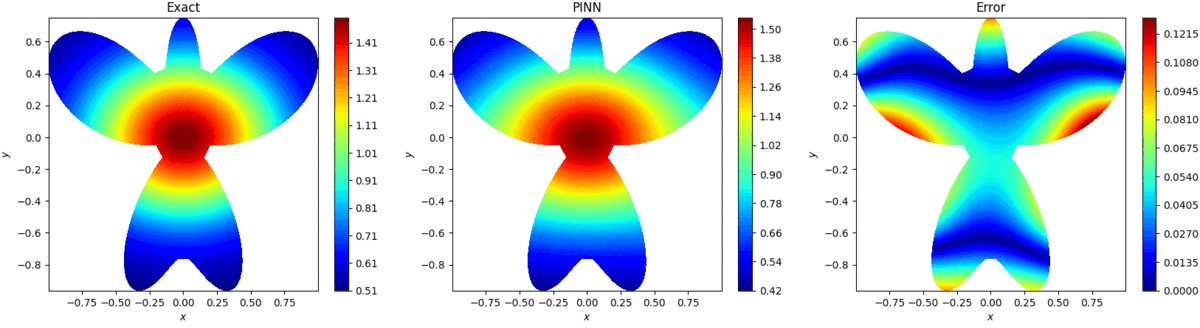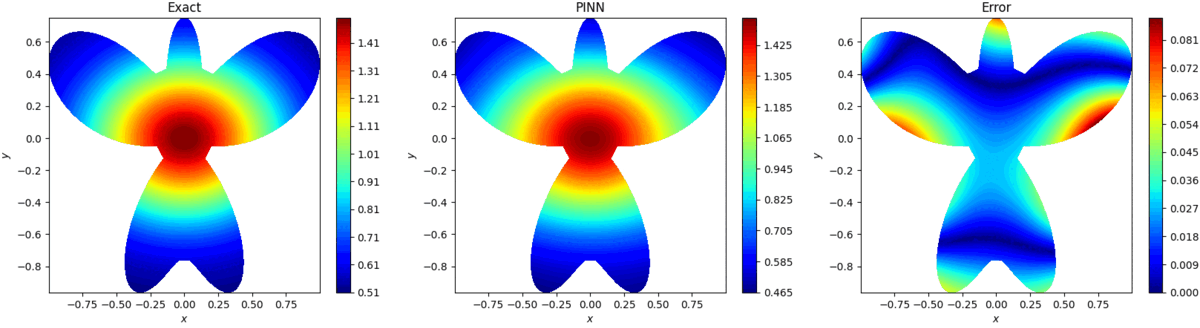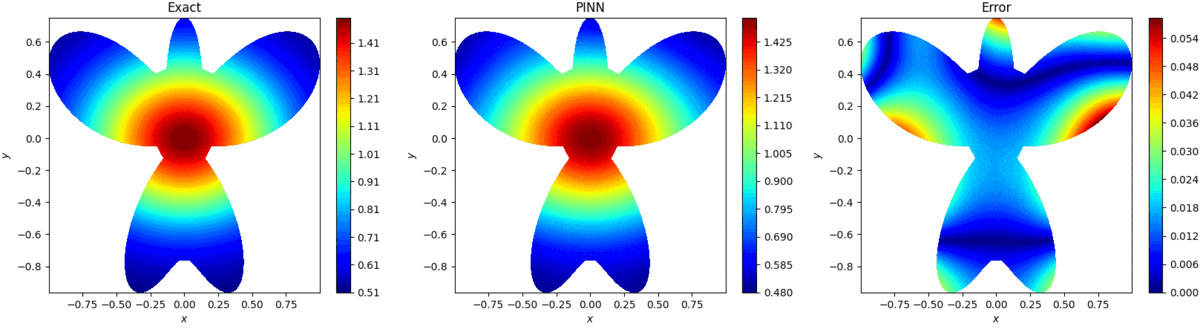
图4:PINN预测结果
版权归原作者 pinn山里娃 所有, 如有侵权,请联系我们删除。