强化学习PPO从理论到代码详解(2)---PPO1和PPO2

在线或离线学习

上一节我们了解了什么是策略梯度，本节开始讲PPO理论之前，我们先提出一个概念，什么在线学习，什么离线学习。

On-policy: Then agent learned and the agent interacting with Environment is the same

Off-policy: Then agent learned and the agent interacting with Environment is not the same

英语确实不好理解，用中文讲就是说，你训练agent需要数据，这些数据可能是你训练的agent和环境交互产生的，那么这就是在线，也可能不是训练的agent产生的，而是另外的agent产生的，这就是离线。

对于一个策略梯度来说在线，离线有什么区别呢？

策略梯度根据上一节的结论，理论上的公式如下，这是一个在线学习的梯度：

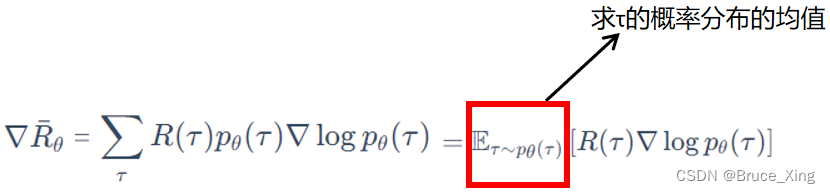
（这里多了一个上一节没有的公式，就是用了一个均值符号）

• 现在我们用一个去收集数据，但是更新了一次之后，就要重新去收集数据，因为之前用的是，梯度上升完了参数就变了，这就是驴唇不对马嘴🙄🙄。而且这样效率也低，为什么，因为强化学习大部分的时间都不是消耗在GPU上，而是和环境的互动上，好不容易互动出来点数据，更新一下又得扔了，能不低效吗。
• 那么转成离线off policy好像就可以解决这个问题，也就是说我们可以从收集数据取更新，因为是固定的，就可以重复利用，大大提升效率。

（ 这里插一嘴，李宏毅老师在这里称作是从on-policy 到 off-policy。PPO给我的感觉也是一个离线的算法，但是easy-rl和很多其他博主都说PPO是一个在线，包括PPO2的论文原文也说PPO比其他的on-policy策略要叼。这里也欢迎讨论）

重要性采样Important Sampling

我们找到了一个提升训练效率的方法， 可以从收集数据取更新，因为是固定的，就可以重复利用，大大提升效率。但是凭什么可以训练啊，你的上一章梯度公式里明明只有一个，你这公式保熟吗？🍉🍉

这里就不得不提到重要性样Important Sampling

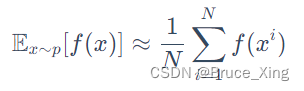
先看这个公式，假设我们有一个函数f(x)，我们从一个分部p中采样，把采样到的的x在带入f(x)。这样即使我们不能对f(x)积分，只要采样够多，我们就可以f(x)在p分布中的均值得到一个均值。

现在我们在假设一种情况，如果我们不能从p中去采样，我们只能从另外一个分部q(x)去采样，可以得到f(x)在p分布中的均值吗？ 答案是肯定的，具体的推导如下：

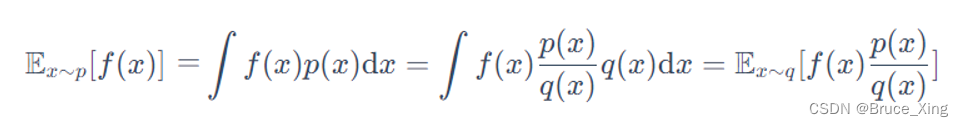
最后结论是这样:

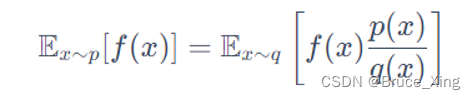
这里看不懂的可以复习下概率论，如果你比较懒也不影响你理解，这里要记住的是，我们已经成功的把从p的采样，改为了从q中的采样。

我们把这个称为重要性权值。如果我们 sample非常多，那么这个重要性权不会有什么影响。但是，but，这是很理想的情况，真是情况不太可能sample的非常均匀且足够，如果这两个分布的方差非常大的话，sample的次数一旦不足，最后结果误差就会非常大！

所以现在提问Q：从p中采样和从q中采样方差Variance一样吗？

根据公式（还是概率论中的公式）来计算一下。

其实p采样和q采样的方差就差了一项重要性权值，，也就是说只要我们保证这两个差别不要太大，结果就还是理想的。举个经典例子，上图

简单来说就是，q分布再右侧概率较大，sample时候容易偏向右，sample出来的正值的点多可能会计算错误，把f(x)均值计算成正的，但实际上它是负值。如果能采样到左边，是一个绝对值很大的负值，就可以很好的纠正最后的计算结果。

on-policy在线 → off policy 离线

经过了这么多的验证，那么我们怎么把PPO从在线推到离线呢，就像这样。其实跟上面说的一样

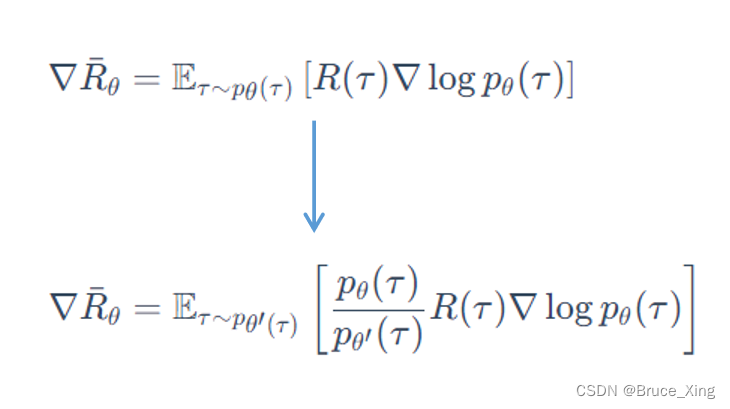
这样整个策略梯度中，我们就可以用来更新。这样就可以让采样大量数据，然后更新多次，大大提升了效率。实际上做策略梯度时，我们并不是用整条轨迹来做更新，而是根据每一个状态-动作（） 对来分别计算。实际更新梯度的过程用的其实就是下式：

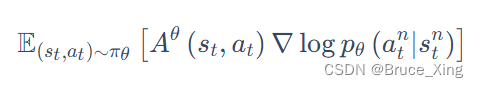
然后在从在线推到离线：

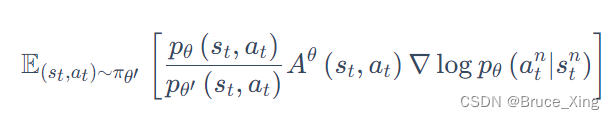
上的，代表是策略参数为与环境交互，但实际上现在我们用的是来采样，现在这个优势就是用来估算的，这里先不管那么多，假设。

然后我们在拆分这两项和

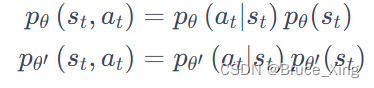
**Q：这里恰一个问题：为什么要拆分呢?**如果不拆分，或者 ，是什么，是我们输入一个动作-状态对，然后输出一个概率，但实际上我们的策略网络并不是这个结构，想一想策略网略是输入一个状态然后输出一个动作的概率分布啊。如果不懂可以接着往后看，看完代码在会后看看以这个问题。

现在梯度下降就可以看做是：

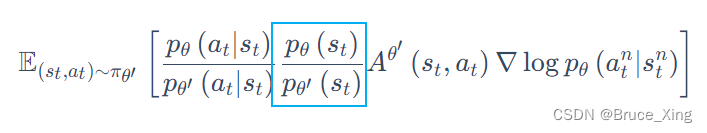
蓝框中的这一项可以消掉，原因可以说是不管是用，还是看到同一状态的概率是一样的，又或者是这两项不好计算，想一想玩游戏时候，游戏画面复杂众多，好像计算某一个画面的出现概率很难计算，这里就直接消掉了，反正最后效果很好，神奇而玄学吧😂😂。

我们把要优化的目标的函数成为,是其中要优化的参数

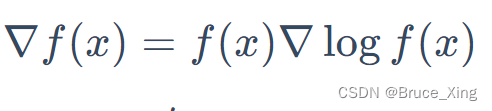
再根据链式法带入，则得到最后的目标函数。（终于得到可以用的目标的函数了🤪🤪，是不是很easy）

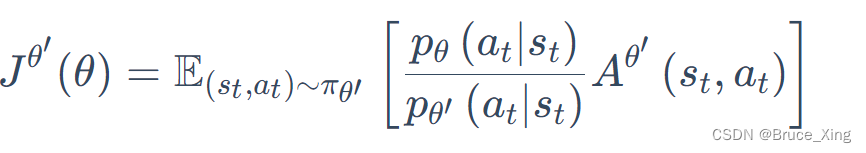
• θ 代表我们要去优化的参数
• θ′ 是指我们用θ′ 做示范，就是现在真正在与环境交互的是θ′

近端策略优化

还记得开始的时候我们写的重要性采样原理吗？里面有很重要的一条的就是θ，θ′ 两个采样样本差异要小，这里就用KL散度（KL divergence）来衡量这个差异，如果你不知道KL散度是什么，可以看这篇。但是，这里我们只要记得KL散度就是用来衡量θ，θ′的差异大小。
初学机器学习：直观解读KL散度的数学概念 - 知乎选自 http://thushv.com，作者：Thushan Ganegedara，机器之心编译。机器学习是当前最重要的技术发展方向之一。近日，悉尼大学博士生 Thushan Ganegedara 开始撰写一个系列博客文章，旨在为机器学习初学者介绍一些…https://zhuanlan.zhihu.com/p/37452654

PPO的公式就是在上面策略梯度的基础上加上一个KL散度的限制

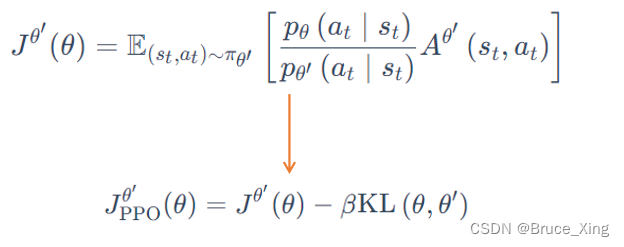
这里KL可以当做一个函数，注意这里θ 与 θ′ 的距离并不是参数上的距离，而是输出动作上的差异。

PPO 有一个前身：信任区域策略优化（trust region policy optimization，TRPO）。TRPO 可表示为如下：

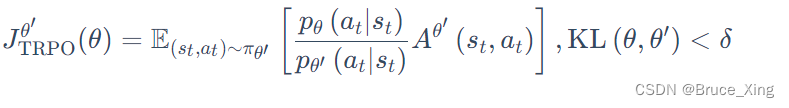
RPO 是很难处理的，因为它把 KL 散度约束当作一个额外的约束，没有放在目标（objective）里面，所以它很难计算。因此我们一般就使用 PPO，而不使用 TRPO 。PPO 与 TRPO 的性能差不多，但 PPO 在实现上比 TRPO 容易得多。

PPO1（近端策略优化惩罚）

PPO 算法有两个主要的变种：近端策略优化惩罚（PPO-penalty）和近端策略优化裁剪（PPO-clip）。

PPO1 是近端策略优化惩罚（PPO-penalty），在 PPO 的论文里面还有一个自适应KL散度（adaptive KL divergence）。这里会遇到一个问题就，即β 要设置为多少？这里easy-rl解释的非常清楚了，我就直接引用了

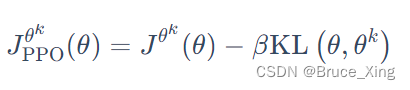
KL 散度的值太大，这就代表后面惩罚的项βKL(,) 没有发挥作用，我们就把β 增大。另外，我们设一个 KL 散度的最小值。如果优化上式以后，KL 散度比最小值还要小，就代表后面这一项的效果太强了，我们怕他只优化后一项，使与 一样，这不是我们想要的，所以我们要减小 β。β 是可以动态调整的，因此我们称之为自适应KL惩罚（adaptive KL penalty）。我们可以总结一下自适应KL惩罚：

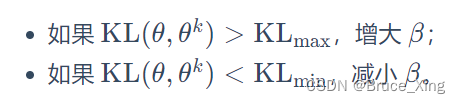
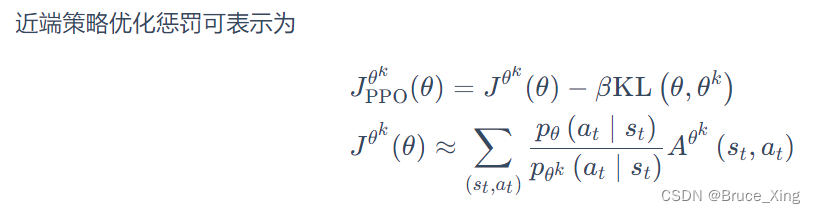
具体不再延伸，因为实际问题我们基本都会用PPO2而不是PPO1。本文的代码也是PPO2，所以向更具体了解的童鞋们可以再去看相关的论文。

PPO2（近端策略优化剪裁）

PPO2可以说是简单粗暴，为什么这么说呢，看公式

计算KL散度太复杂，我干脆直接限定输出动作概率分布比值的最大最小值，就用min,和clip中的这一串，整个式子中：

• min 是在第一项与第二项里面选择比较小的项
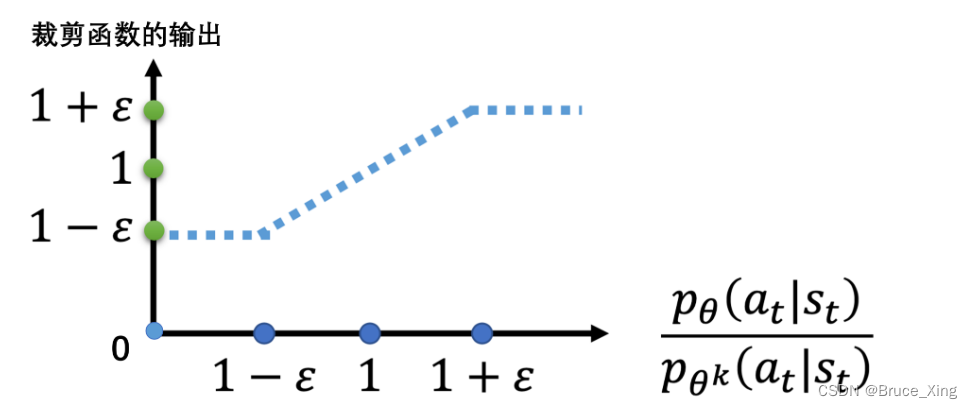
• 有一个裁剪clip函数（代码中非常好实现，比如用numpy就有对应的api），裁剪函数是指，在括号里面有3项，如果第一项小于第二项，那就输出 1−ε；第一项如果大于第三项，那就输出 1+ε
• ε 是一个超参数，是我们要调整的，

就是这么简单粗暴，但是，实际效果却非常好！对于clip函数，再放一张图让大家便于理解：

那么A是如何影响结果的呢，直接放图：

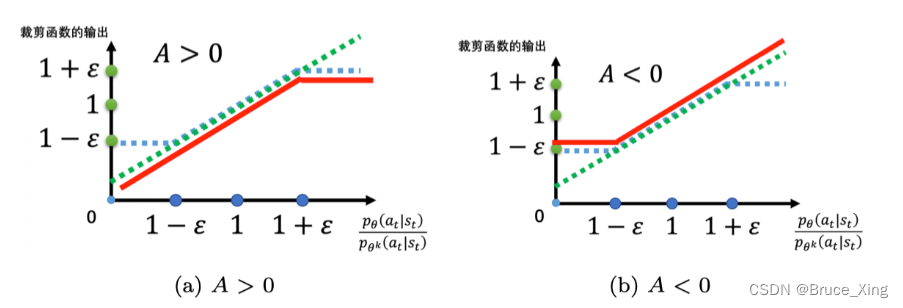
PPO2用了min，用了clip其实还是不想让 和，差距过大，那么PPO2是怎么做到的？

• 如果 A > 0，也就是某一个状态-动作对是好的，我们希望增大这个状态-动作对的概率。也就是，我们想让 越大越好，但它与 的比值不可以超过1+ε。根据重要性采样，如果比值过大很可能会导致结果不准确。
• 如果 A < 0，也就是某一个状态-动作对是不好的，那么我们希望把 减小。如果比 还大，那我们就尽量把它减小1−ε 的时候停止，此时不用再减得更小。

这样和差距就不会太大。

这一章节我们分析了PPO1，PPO2，基本上所用到的理论都覆盖到了，下一章我们将一步步的写PPO2的代码。