这几天被Mamba刷屏了,又由于本人是做视觉方面任务的,固来看看mamba在视觉上的应用。
今天分享的是Vision Mamba: Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model
论文网址:https://arxiv.org/pdf/2401.09417.pdf
代码网址: https://github.com/hustvl/Vim
本文将涉及:
1.Mamba的基础
2.Vision Mamba 论文简读
3.Vision Mamba 论文中figure2 和伪代码1的详细解读,作用,对应github代码部分的分析。
本文未涉及:
Vision Mamba的实机环境配置过程以及实机运行(训练和测试),
笔者尝试不同环境下配置Vision Mamba(Win10(
失败
\textcolor{red}{失败}
失败),Linux(
成功
\textcolor{red}{成功}
成功)。敬请期待。
Win10下Vision Mamba的配置,最后的问题和这个博主一样:https://blog.csdn.net/weixin_46135891/article/details/137141378
而且也看不太懂 compiler.py 里面对应代码的执行结果,不知如何修改。
Linux的方面的配置,参考CSDN或者官方的readme 很容易就能配出来。
阅读Vision Mamba,首先需要Mamba的相关基础,笔者首先推荐读者阅读下篇博客,写的非常好:
一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba
后续笔者的第一部分—Mamba的基础也大多来源于此。
目录
Mamba基础
参考:https://blog.csdn.net/v_JULY_v/article/details/134923301
写的真的很好。
CNN,Transformer和RNN的优缺点
CNN
优点:由于卷积操作简单,可并行,训练较快。占用内存较小
缺点:在局部区域提取特征,缺少全局感受野。
Transformer
优点:全局区域提取特征,感受野更大;高度并行化,训练相对较快(但是训练的epoch相比CNN增加不少)
缺点:处理序列的时间复杂度为
O
(
L
2
D
)
O(L^2D)
O(L2D) ,其中L是序列长度(图像任务中即W*H),D是通道维度。计算复杂度和序列长度的平方
N
2
N^2
N2成正比。
RNN
优点:因为隐状态,RNN具有时间信息;推理速度较快。
缺点:每次训练时,当前时刻的隐状态依赖于上一个时刻的隐状态,训练无法并行,训练很慢。
Mamba的前身—SSM
讲Mamba前,先看看Structured Space Model(SSM)即状态空间模型。
首先定义如下变量:
X
t
X_t
Xt: t时刻的输入(连续数据),
H
t
H_t
Ht: t时刻的潜在状态/隐状态,
Y
t
Y_t
Yt: t时刻的输出
定义如下公式:
H
t
=
A
∗
H
t
−
1
+
B
∗
X
t
H_t=A*H_{t-1}+B*X_t
Ht=A∗Ht−1+B∗Xt
Y
t
=
C
∗
H
t
+
D
∗
X
t
Y_t=C*H_t+D*X_t
Yt=C∗Ht+D∗Xt
其中
A
,
B
,
C
,
D
A,B,C,D
A,B,C,D是四个矩阵,可学习参数,表示对应的矩阵操作。
回看下RNN
H
t
=
t
a
n
h
(
W
∗
H
t
−
1
+
A
∗
X
t
)
H_t=tanh(W*H_{t-1}+A*X_t)
Ht=tanh(W∗Ht−1+A∗Xt)
Y
t
=
F
(
H
t
)
Y_t=F(H_t)
Yt=F(Ht)
这样对比来看,其实RNN和SSM的思想是差不多的,都会生成隐状态。
后续会讲到和RNN的区别,现在先回过来看SSM
其中D矩阵类似于跳跃连接,如果没有D矩阵的话,SSM优化如下:
H
t
=
A
∗
H
t
−
1
+
B
∗
X
t
H_t=A*H_{t-1}+B*X_t
Ht=A∗Ht−1+B∗Xt
Y
t
=
C
∗
H
t
Y_t=C*H_t
Yt=C∗Ht
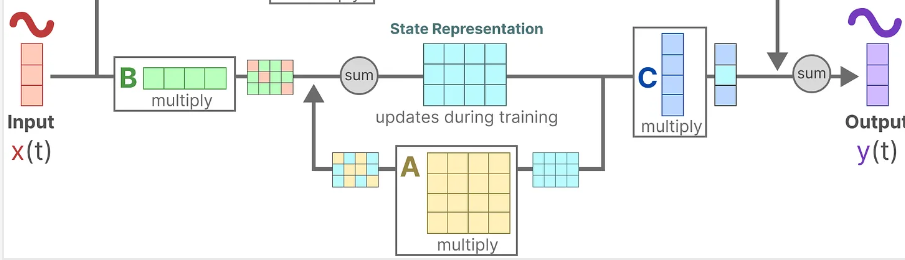
SSM—>S4—Structured State Spaces for Sequences
S4:Structured State Spaces for Sequences,序列的结构化状态空间。相比于SSM( State Space Module)多了两个S,分别是Structured(结构化) 和Sequences(序列)。
既然是处理序列数据,那么公式中输入X肯定是离散的情况,那如何处理呢?
作者这里采用了“零阶保持技术”,其大致执行过程如下: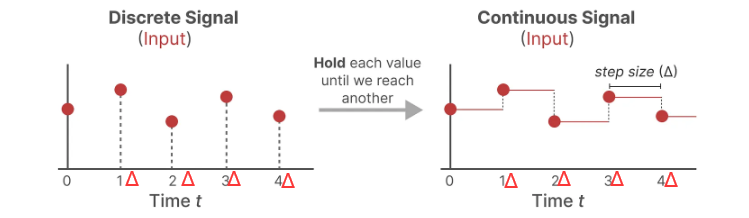
每次收到离散信号时,都会保留其值一段时间,直到收到新的离散信号,这样操作,输入的离散数据就会变成连续数据。
其中“保持一段时间” 称之为步长Δ,具体实现是,其是可学习参数。
SSM中加入了零阶保持技术的处理过程如下:
1 对离散输入x进行零阶保持(步长Δ),得到连续输入X’
2 对连续输入X’ 进行 连续SSM公式,得到连续输出Y’
3 对连续输出Y’ 按照步长Δ 采样,得到离散输出y
或者另一种处理过程:
1 对连续SSM公式中的A,B矩阵按照步长Δ采样,得到离散的
A
ˉ
,
B
ˉ
\bar{A},\bar{B}
Aˉ,Bˉ
2 将
A
ˉ
,
B
ˉ
\bar{A},\bar{B}
Aˉ,Bˉ做为SSM公式中新的A,B,即可得到离散型SSM
3 对离散输入x进行离散型SSM,得到离散输出
作者更加推荐的是下面这种方式
PS:离散方法除了上面提到的“零阶保持技术”,还有其它有效的离散化方法,如欧拉方法、零阶保持器(Zero-order Hold, ZOH)方法或双线性方法。欧拉方法是最弱的,但在后两种方法之间的选择是微妙的。事实上,S4论文采用的是双线性方法,但Mamba使用的是ZOH。
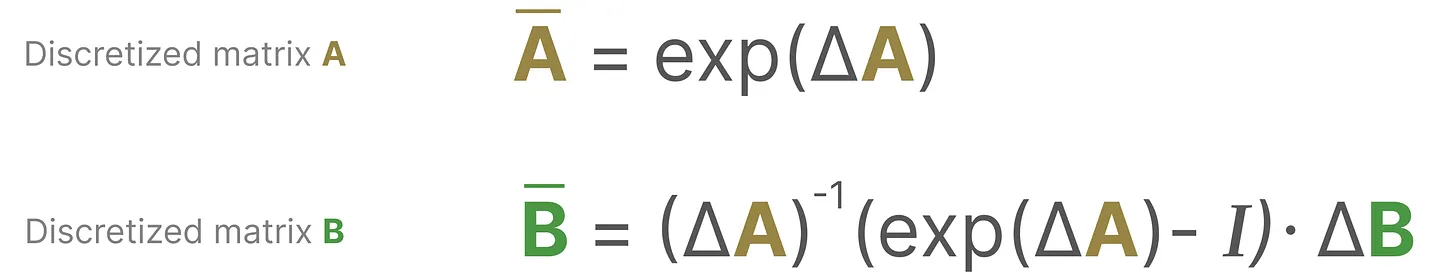
注意:在保存中间结果时,仍然保存矩阵A,B的连续形式(而非离散化版本),只是在训练过程中,连续表示被离散化。
离散SSM公式:
H
t
=
A
ˉ
∗
H
t
−
1
+
B
ˉ
∗
X
t
H_t=\bar{A}*H_{t-1}+\bar{B}*X_t
Ht=Aˉ∗Ht−1+Bˉ∗Xt
Y
t
=
C
∗
H
t
Y_t=C*H_t
Yt=C∗Ht
为了减化SMM,此处也同样不考虑跳跃连接。
接下来考虑S4训练和测试的情况:
假设以
y
2
y_2
y2为例:
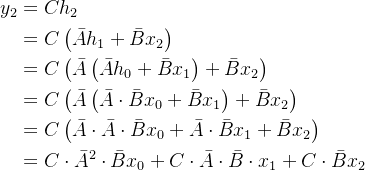
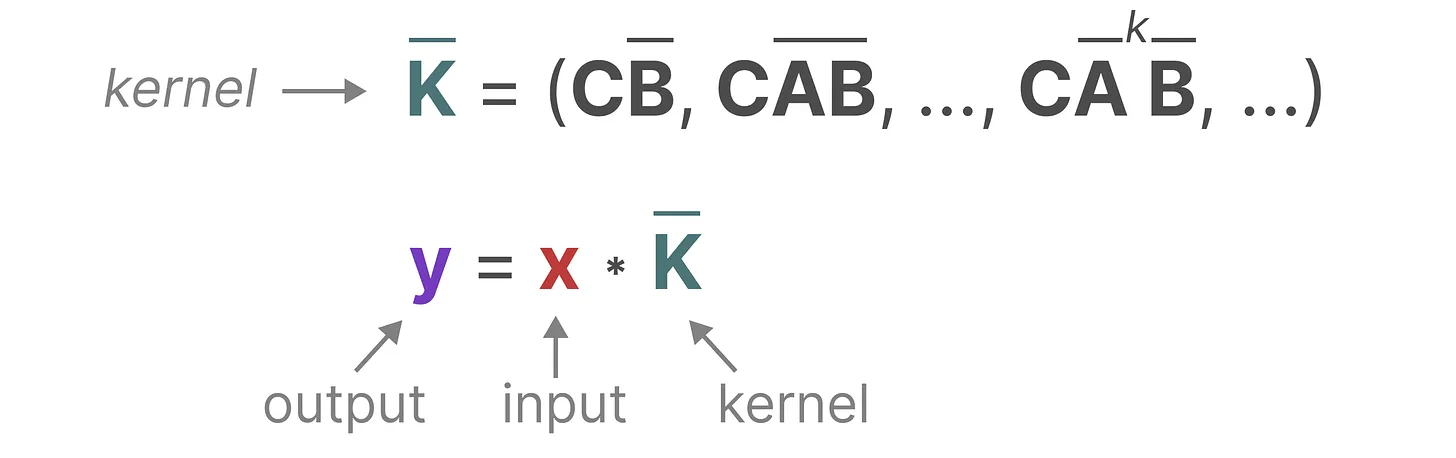
这样就写成了卷积的形式,也就是说S4可以并行训练了。推理方面还是采用RNN的方式,因为如果按照卷积形式来推理,速度还是比较慢的。
最后就是”基于HiPPO处理长序列“的新思想,主要作用在了
A
A
A矩阵的初始化上,这样初始化能方便A矩阵更好的学习。具体内容可以参考分析:https://blog.csdn.net/v_JULY_v/article/details/134923301
S4—>Mamba即S6----- S4+Selective Scan algorithm
Mamba则在S4的基础上加上了Selective Scan (选择性扫描)算法, 亦在让Mamba像Attention那样能够关注输入数据。
可以先看下S4中维度的变化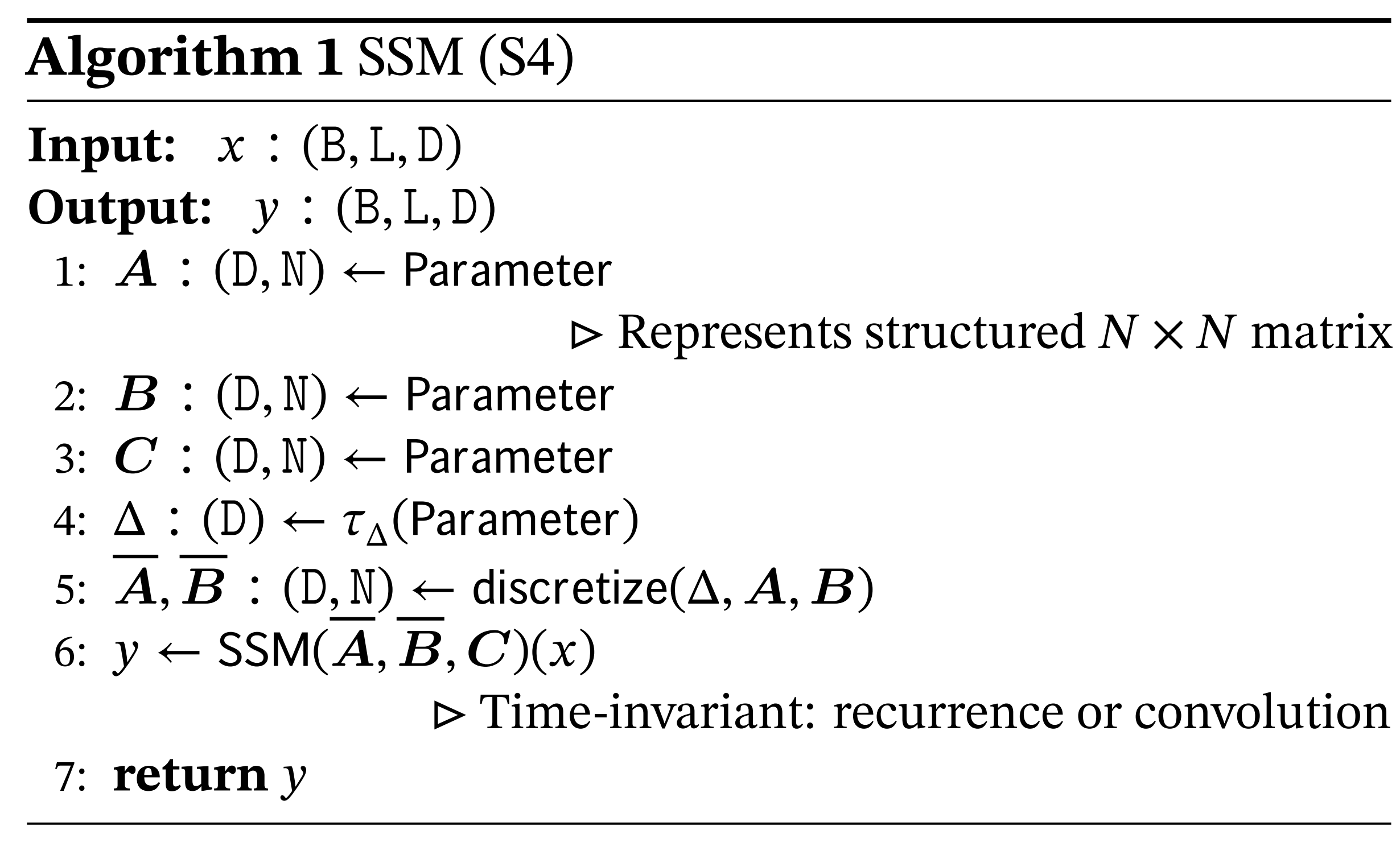
其中
A
,
B
,
C
A,B,C
A,B,C矩阵是
D
∗
N
D*N
D∗N的可学习参数。 其中D表示隐藏状态的维度,N表示SSM的维度。
为什么说S4没有选择性扫描呢?----------------------可以类比静态卷积
因为训练好A,B,C后,参数固定了。这就好比是一个卷积操作
Y
=
C
o
n
v
(
X
)
Y=Conv(X)
Y=Conv(X) 卷积的参数训练完固定后,那么卷积操作就是静态的了。此时卷积就没有“选择性”这一说。
那什么操作又选择性呢?-----------Attention,以self-attention为例:
Y
=
S
o
f
t
m
a
x
(
Q
∗
K
T
)
∗
V
/
s
q
r
t
(
d
k
)
;
Y= Softmax(Q*K^T)*V / sqrt(d_k);
Y=Softmax(Q∗KT)∗V/sqrt(dk);
Q
=
W
Q
∗
X
,
K
=
W
K
∗
X
,
V
=
W
V
∗
X
Q=W^Q*X ,K=W^K*X,V=W^V*X
Q=WQ∗X,K=WK∗X,V=WV∗X
训练好后,即使里面的
W
Q
,
W
K
,
W
V
W^Q,W^K,W^V
WQ,WK,WV的参数固定了。但里面有个softmax激活函数根据不同的输入会得到不同的Softmax(Q*K^T)值,最后在乘以V得到最后结果。所以说Attention就是有“选择性的”。
那如何让S6有选择性呢?------------加个softmax?这是显然不行的,因为加上了softmax,隐变量就无法并行化计算,退化成了RNN。这也是因为RNN无法并行化的原因,有tanh函数激活函数。
作者的想法是,扩增B,C和Δ的维度:
其实这样更好理解, S4+线性层投影 ≈ S6
其中的A矩阵的维度不变,还是
D
∗
N
D*N
D∗N的可学习矩阵,但
B
,
C
,
Δ
B,C,Δ
B,C,Δ的构造发生了变化,Mamba即S6是通过对输入X进行线性层操作(比如 Conv1d,Linear)操作来得到
B
,
C
,
Δ
B,C,Δ
B,C,Δ。
这同样也导致了后续的
A
ˉ
,
B
ˉ
\bar{A},\bar{B}
Aˉ,Bˉ维度的变化。
现在来分析下S6为什么具有"选择性"。
原来的
B
ˉ
.
s
h
a
p
e
=
=
D
∗
N
−
−
−
>
1
∗
1
∗
D
∗
N
\bar{B}.shape==D*N--->1*1*D*N
Bˉ.shape==D∗N−−−>1∗1∗D∗N B组L个D维度的序列,只有1个D维度的SSM(它的维度是N),那么每个序列对应的B是相同的。
现在的
B
ˉ
.
s
h
a
p
e
=
=
B
∗
L
∗
D
∗
N
\bar{B}.shape== B*L*D*N
Bˉ.shape==B∗L∗D∗N B组L个D维度的序列,有B组L个D维度的SSM(它的维度是N),那么每个序列对应的B是不同的。
下面这种“每个序列对应的B是不同的。” 就导致了S6的“选择性”。
S6还有其它的优点,比如:硬件感知算法,并行扫描(并行累加)加速训练。但笔者这里没怎么看懂,怕讲错,也不讲了
Vision Mamba
上面大概是Mamba的进化史:SSM–>S4–>S6.
SSM(连续性)+离散化+HIPPO+训练测试技巧=S4
S4+线性层投影+硬件感知并行加速=S6即Mamba
其中涉及的内容非常的多。现在有个印象即可,笔者还是偏实战的,理论方面太枯燥了。所以现在来看Mamba在视觉任务上的实战-----Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Mode
摘要
简单看看,
文章介绍了Vim模型,这是一种新的通用视觉基础模型,它利用双向Mamba块(bidirectional Mamba blocks (Vim))和位置嵌入 (position embeddings)来处理图像序列,并在ImageNet分类、COCO对象检测和ADE20K语义分割任务上取得了比现有的视觉Transformer模型(如DeiT)更好的性能。
指出了Mamba时间复杂度与序列长度是线性的。而Transformer的时间复杂度是与序列长度乘二次方关系。强调 ViM 更好,更快,更节省内存开销。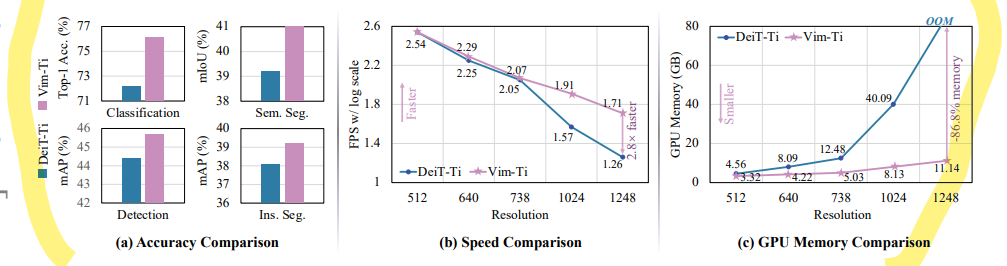
引言
提到了mamba直接用到视觉任务里面的一些缺点:
单向建模:Mamba原本用于语言处理,通常是单向的,这意味着它只能捕捉从前到后的序列依赖。—>解决方法,后续在具体实现中提出了双向的概念
位置感知的缺失:与transformer一样,处理一维的序列数据时,无法感知原始图像数据里面各像素间的位置信息。—>解决方法,添加位置编码
方法
该节中涉及到的公式,和上面将Mamba的基础里面涉及的公式基本一致,在此不做赘述,如果Mamba的基础有个大概了解的话,这里的公式应该都能看懂。
公式1是连续SSM的公式
公式2,公式3
是连续SSM+ 离散化后==S4的公式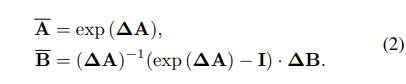
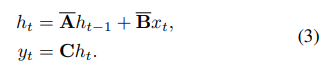
公式4 是 S4训练时并行化的公式。
3.2 Vision Mamba公式

公式5,这里和Vision Transformer类比。对于输入的图像,首先进行patch+embedding+position 的操作。而且还在图像序列的第一个位置加入了分类头
t
c
l
s
t_{cls}
tcls。
shape变化:
(
H
,
W
,
C
)
(H,W,C)
(H,W,C)–>
(
J
,
P
2
∗
C
)
(J , P^2 *C)
(J,P2∗C) 其中J 就是序列长度, P是一个图像块的大小
公式6,这里是Vision Mamba的迭代公式,循环迭代
l
l
l层Vision Mamba,后续详解。 
Vision Mabma Block

最关键的部分,对应3.2中公式6的
V
i
m
(
⋅
)
Vim(\cdot)
Vim(⋅)
其中
B
−
−
−
b
a
t
c
h
s
i
z
e
B---batchsize
B−−−batchsize
M
−
−
−
序列长度
M--- 序列长度
M−−−序列长度
D
−
−
−
序列维度
D---序列维度
D−−−序列维度
E
−
−
−
升维后序列维度
E---升维后序列维度
E−−−升维后序列维度
N
−
−
−
S
S
M
的维度
N---SSM的维度
N−−−SSM的维度
Vision Mamba 编码器:这些嵌入的 patches 作为 token 序列输入到 Vim 编码器。编码器的结构如右侧所示,主要包含以下部分:
以下是笔者对着上面的伪代码步骤化画的图,其中只画了forward分支,backward分支基本一样,只是在执行之前先把x的序列逆序,再送入到S4 Module。其中红色框出来的地方,就对应着Vision Mamba里面的forward/backward SSM。
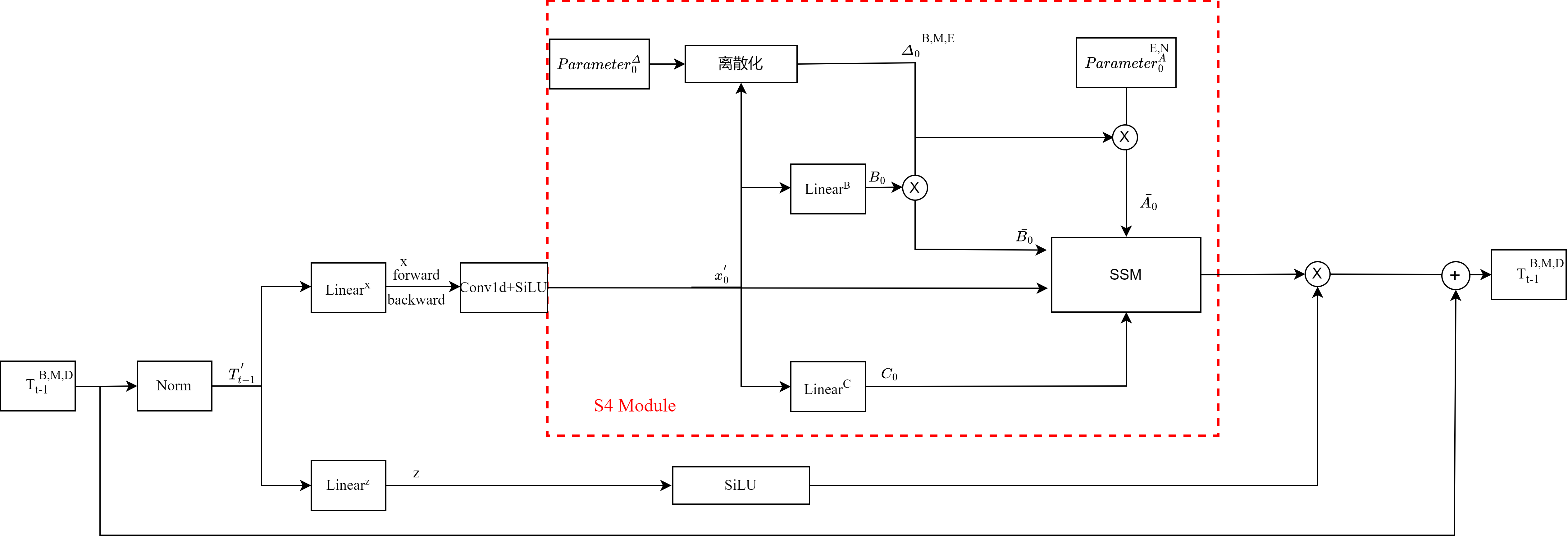
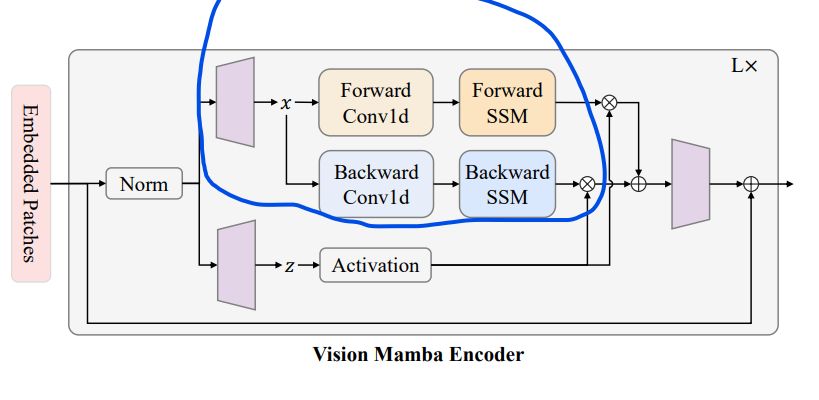
标准化 (Norm):编码器内部首先对 token 序列进行标准化。
激活:对序列进行激活函数处理,这里没有具体指明使用哪种激活函数,但通常是非线性激活函数,如 ReLU 或者 SiLU。
双向处理:模型中的每个 token 被送往两个方向处理:
前向卷积 (Forward Conv1d):处理序列的前向部分。
后向卷积 (Backward Conv1d):处理序列的后向部分。
状态空间模型 (SSM):前向和后向处理的结果分别通过状态空间模型,这可以帮助捕获长距离的依赖关系。
z分支那里可以当作是门控操作。
笔者一开始对FowardSSM 很疑惑,作者为什么不展开的详细一点。可能是:展开后比较麻烦,如笔者画的流程图一样。其次,在代码具体实现中,由于Mamba(S4)的代码已经封装好了,Vision Mamba作者在调用的时候其实也是直接调用了封状的函数。如下:
在https://github.com/hustvl/Vim/blob/main/vim/models_mamba.py#L162
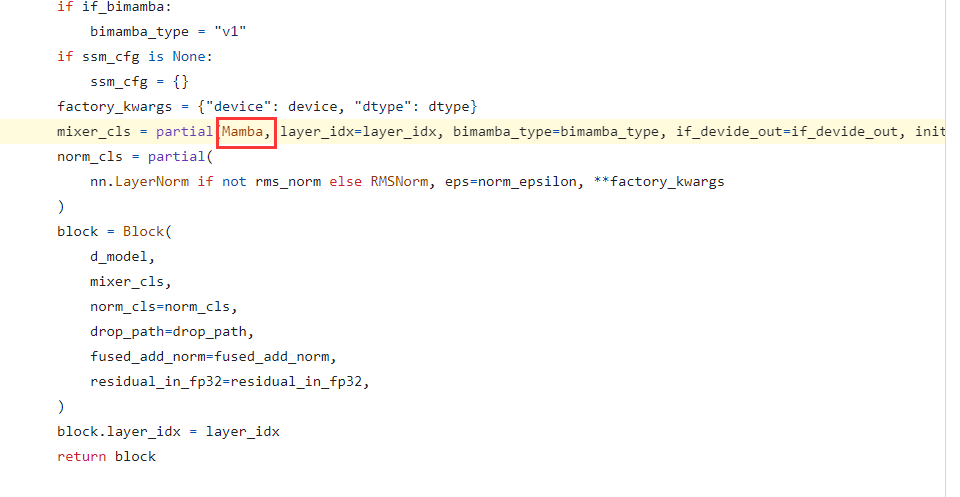
因此如果要看具体的Mamba(S4) 代码,还是要回到最开始的Mamba论文里面给出的源码地址。 在Vision Mamba中由于高度封状,看不到Mamba内具体的执行过程。
顺便说明Vision Mamba源码中下 forward和backward 的具体实现:
其中上图的第 491行的结果就是forward后的结果。 494行中对输入X 进行在dim=1(序列长度的维度) 进行反转,然后送入backward分支。
后续的结果,消融实验,硬件加速策略本文就不细读了。
参考
一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba
Vision Mamba 超详细解读
欢迎指正
因为本文主要是本人用来做的笔记,顺便进行知识巩固。如果本文对你有所帮助,那么本博客的目的就已经超额完成了。
本人英语水平、阅读论文能力、读写代码能力较为有限。有错误,恳请大佬指正,感谢。
欢迎交流
邮箱:refreshmentccoffee@gmail.com
版权归原作者 啊 昃 所有, 如有侵权,请联系我们删除。