自 2017 年发表“ Attention Is All You Need ”论文以来,Transformer 架构一直是自然语言处理 (NLP) 领域的基石。它的设计多年来基本没有变化,随着旋转位置编码 (RoPE) 的引入,2022年标志着该领域的重大发展。
旋转位置嵌入是最先进的 NLP 位置嵌入技术。大多数流行的大型语言模型(如 Llama、Llama2、PaLM 和 CodeGen)已经在使用它。在本文中,我们将深入探讨什么是旋转位置编码,以及它们如何巧妙地融合绝对位置嵌入和相对位置嵌入的优点。
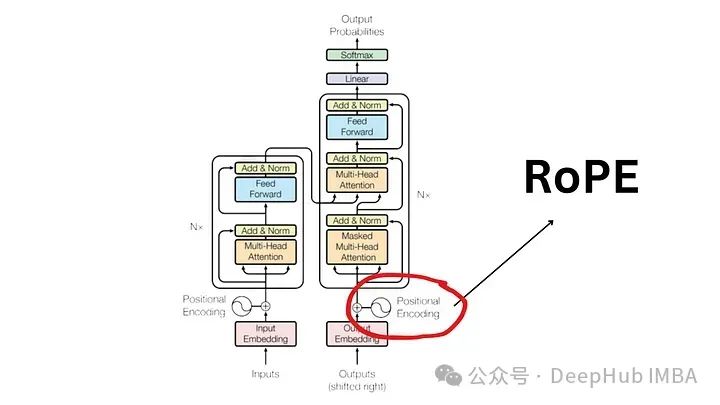
位置编码的需求
为了理解 RoPE 的重要性,我们首先回顾一下为什么位置编码至关重要。Transformer 模型根据其固有的设计,不会考虑输入标记的顺序。
例如,像“the dog chases the pig ”和“the pig chases the dogs”这样的短语虽然含义不同,但由于它们被视为一组无序的标记,因此被视为无法区分。为了维护序列信息及其含义,需要一个表示来将位置信息集成到模型中。
绝对位置编码
在句子的上下文中,假设我们有一个代表一个单词的嵌入。为了对其位置进行编码,需要使用另一个具有相同维度的向量,其中每个向量唯一地代表句子中的一个位置。例如,为句子中的第二个单词指定特定向量。所以每个句子位置都有其独特的向量。然后通过将词嵌入与其相应的位置嵌入求和来形成 Transformer 层的输入。
有两种主要方法来生成这些嵌入:
- 从数据中学习:在这里,位置向量是在训练过程中学习的,就像其他模型参数一样。我们为每个位置(例如从 1 到 512)学习一个唯一的向量。这引入了一个限制——最大序列长度受到限制。如果模型仅学习到位置 512,则它无法表示比该位置更长的序列。
- 正弦函数:此方法涉及使用正弦函数为每个位置构建唯一的嵌入。尽管这种构造的细节很复杂,但它本质上为序列中的每个位置提供了独特的位置嵌入。实证研究表明,从数据中学习和使用正弦函数可以在现实世界模型中提供相当的性能。
绝对位置编码的局限性
尽管使用广泛但绝对位置嵌入也并非没有缺点:
- 有限序列长度:如上所述,如果模型学习到某个点的位置向量,它本质上不能表示超出该限制的位置。
- 位置嵌入的独立性:每个位置嵌入都是独立于其他位置嵌入的。这意味着在模型看来,位置 1 和 2 之间的差异与位置 2 和 500 之间的差异相同。但是其实位置 1 和 2 应该比位置 500 相关性更密切,位置 500 距离明显更远。这种相对定位的缺乏可能会阻碍模型理解语言结构的细微差别的能力。
相对位置编码
相对位置位置不是关注标记在句子中的绝对位置,而是关注标记对之间的距离。该方法不会直接向词向量添加位置向量。而是改变了注意力机制以纳入相对位置信息。
最经典得案例就是T5(Text-to-Text Transfer Transformer)是一种利用相对位置嵌入的著名模型。T5 引入了一种处理位置信息的微妙方式:
- 位置偏移的偏差: T5 使用偏差(浮点数)来表示每个可能的位置偏移。例如,偏差 B1 可能表示任意两个相距一个位置的标记之间的相对距离,无论它们在句子中的绝对位置如何。
- 自注意力层中的集成:该相对位置偏差矩阵被添加到自注意力层中的查询矩阵和关键矩阵的乘积中。这确保了相同相对距离的标记始终由相同的偏差表示,无论它们在序列中的位置如何。
- 可扩展性:该方法的一个显着优点是其可扩展性。它可以扩展到任意长的序列,这比绝对位置嵌入有明显的优势。
相对位置编码的局限性
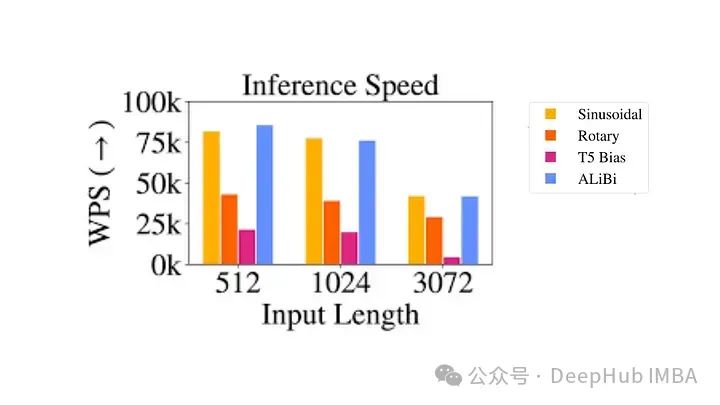
尽管它们在理论上很有吸引力,但相对位置编码得问题很严重
- 计算效率低下:必须创建成对的位置编码矩阵,然后执行大量张量操作以获得每个时间步的相对位置编码。特别是对于较长的序列。这主要是由于自注意力层中的额外计算步骤,其中位置矩阵被添加到查询键矩阵中。
- 键值缓存使用的复杂性:由于每个附加令牌都会改变每个其他令牌的嵌入,这使得 Transformer 中键值缓存的有效使用变得复杂。使用 KV 缓存的一项要求是已经生成的单词的位置编码,****在生成新单词时不改变(绝对位置编码提供)因此相对位置编码不适合推理,因为每个标记的嵌入会随着每个新时间步的变化而变化。
由于这些工程复杂性,位置编码未得到广泛采用,特别是在较大的语言模型中。
旋转位置编码 (RoPE)?
RoPE 代表了一种编码位置信息的新方法。传统方法中无论是绝对方法还是相对方法,都有其局限性。绝对位置编码为每个位置分配一个唯一的向量,虽然简单但不能很好地扩展并且无法有效捕获相对位置;相对位置编码关注标记之间的距离,增强模型对标记关系的理解,但使模型架构复杂化。
RoPE巧妙地结合了两者的优点。允许模型理解标记的绝对位置及其相对距离的方式对位置信息进行编码。这是通过旋转机制实现的,其中序列中的每个位置都由嵌入空间中的旋转表示。RoPE 的优雅之处在于其简单性和高效性,这使得模型能够更好地掌握语言语法和语义的细微差别。
旋转矩阵源自我们在高中学到的正弦和余弦的三角性质,使用二维矩阵应该足以获得旋转矩阵的理论,如下所示!
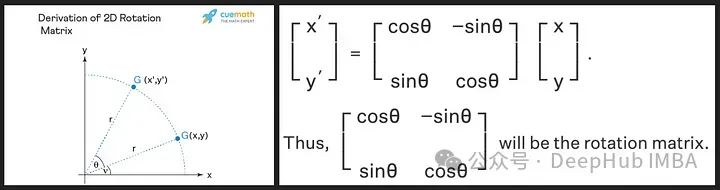
我们看到旋转矩阵保留了原始向量的大小(或长度),如上图中的“r”所示,唯一改变的是与x轴的角度。
RoPE 引入了一个新颖的概念。它不是添加位置向量,而是对词向量应用旋转。旋转角度 (θ) 与单词在句子中的位置成正比。第一个位置的向量旋转 θ,第二个位置的向量旋转 2θ,依此类推。这种方法有几个好处:
- 向量的稳定性:在句子末尾添加标记不会影响开头单词的向量,有利于高效缓存。
- 相对位置的保留:如果两个单词在不同的上下文中保持相同的相对距离,则它们的向量将旋转相同的量。这确保了角度以及这些向量之间的点积保持恒定
RoPE 的矩阵公式
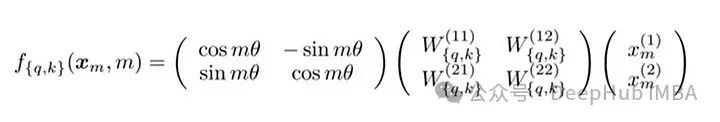
RoPE的技术实现涉及到旋转矩阵。在 2D 情况下,论文中的方程包含一个旋转矩阵,该旋转矩阵将向量旋转 Mθ 角度,其中 M 是句子中的绝对位置。这种旋转应用于 Transformer 自注意力机制中的查询向量和键向量。
对于更高维度,向量被分成 2D 块,并且每对独立旋转。这可以被想象成一个在空间中旋转的 n 维。听着这个方法好好像实现是复杂,其实不然,这在 PyTorch 等库中只需要大约十行代码就可以高效的实现。
importtorch
importtorch.nnasnn
classRotaryPositionalEmbedding(nn.Module):
def__init__(self, d_model, max_seq_len):
super(RotaryPositionalEmbedding, self).__init__()
# Create a rotation matrix.
self.rotation_matrix=torch.zeros(d_model, d_model, device=torch.device("cuda"))
foriinrange(d_model):
forjinrange(d_model):
self.rotation_matrix[i, j] =torch.cos(i*j*0.01)
# Create a positional embedding matrix.
self.positional_embedding=torch.zeros(max_seq_len, d_model, device=torch.device("cuda"))
foriinrange(max_seq_len):
forjinrange(d_model):
self.positional_embedding[i, j] =torch.cos(i*j*0.01)
defforward(self, x):
"""
Args:
x: A tensor of shape (batch_size, seq_len, d_model).
Returns:
A tensor of shape (batch_size, seq_len, d_model).
"""
# Add the positional embedding to the input tensor.
x+=self.positional_embedding
# Apply the rotation matrix to the input tensor.
x=torch.matmul(x, self.rotation_matrix)
returnx
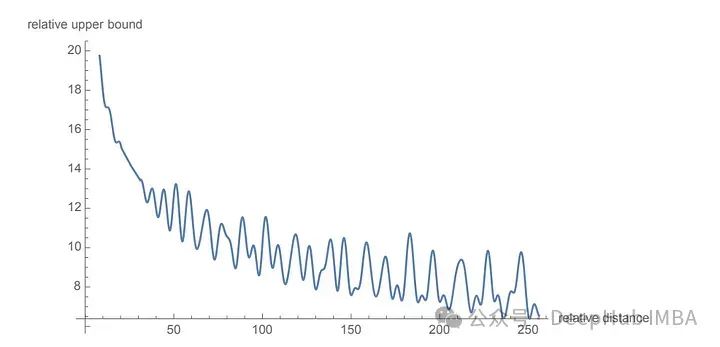
为了旋转是通过简单的向量运算而不是矩阵乘法来执行。距离较近的单词更有可能具有较高的点积,而距离较远的单词则具有较低的点积,这反映了它们在给定上下文中的相对相关性。
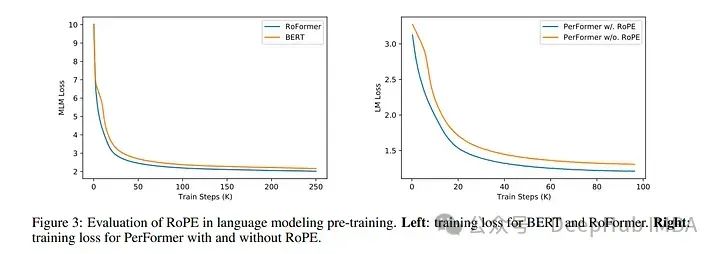
使用 RoPE 对 RoBERTa 和 Performer 等模型进行的实验表明,与正弦嵌入相比,它的训练时间更快。并且该方法在各种架构和训练设置中都很稳健。
最主要的是RoPE是可以外推的,也就是说可以直接处理任意长的问题。在最早的llamacpp项目中就有人通过线性插值RoPE扩张,在推理的时候直接通过线性插值将LLAMA的context由2k拓展到4k,并且性能没有下降,所以这也可以证明RoPE的有效性。
代码如下:
import transformers
old_init = transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__
def ntk_scaled_init(self, dim, max_position_embeddings=2048, base=10000, device=None):
#The method is just these three lines
max_position_embeddings = 16384
a = 8 #Alpha value
base = base * a ** (dim / (dim-2)) #Base change formula
old_init(self, dim, max_position_embeddings, base, device)
transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__ = ntk_scaled_init
总结
旋转位置嵌入代表了 Transformer 架构的范式转变,提供了一种更稳健、直观和可扩展的位置信息编码方式。
RoPE不仅解决了LLM context过长之后引起的上下文无法关联问题,并且还提高了训练和推理的速度。这一进步不仅增强了当前的语言模型,还为 NLP 的未来创新奠定了基础。随着我们不断解开语言和人工智能的复杂性,像 RoPE 这样的方法将有助于构建更先进、更准确、更类人的语言处理系统。
RoPE论文:
https://arxiv.org/abs/2104.09864
扩展LLAMA的context的文章: