1.引言
1.1.背景
当机器需要从经验中汲取知识时,概率建模成为了一个至关重要的工具。它不仅为理解学习机制提供了理论框架,而且在实际应用中,特别是在设计能够从数据中学习的机器时,概率建模展现出了其独特的价值。概率框架的核心在于它如何处理模型和预测中的不确定性,这种能力在科学数据分析、机器学习、机器人技术、认知科学以及人工智能等多个领域中都扮演着至关重要的角色。
1.2.内容提要
本文旨在为读者提供一个关于概率建模框架的深入介绍,并探讨该领域的一些前沿进展。特别地,我们将探讨概率编程如何使得建模过程更加灵活和高效,贝叶斯优化如何帮助我们在不确定性环境中做出更明智的决策,数据压缩如何帮助我们更有效地存储和传输信息,以及自动模型发现如何助力我们更快速地找到最适合数据的模型。这些进展不仅推动了机器学习领域的发展,也为解决实际问题提供了新的视角和方法。
在探讨机器学习的核心时,本篇文章深入分析了概率框架和贝叶斯推理的基本概念。文章着重强调了不确定性在机器学习中的核心地位,并指出它对于提升算法性能至关重要。同时,文章还介绍了当前研究领域的几个前沿方向,这些方向不仅推动了机器学习的发展,也为解决实际问题提供了新的思路和方法。
首先,文章讨论了概率编程,这是一种灵活的建模工具,它允许我们更直观地表示和推理不确定性。通过概率编程,我们可以构建复杂的模型,以捕捉数据中的复杂模式和结构。
其次,贝叶斯优化作为一种在不确定性环境中进行决策的有效方法,被广泛应用于各种机器学习应用中。它能够帮助我们在资源有限的情况下,通过迭代地收集数据并更新模型,来找到最优解。
此外,概率数据压缩作为数据处理的关键技术之一,通过利用数据中的冗余和相关性来减少存储和传输成本。在大数据和云计算时代,概率数据压缩显得尤为重要。
文章还提到了从数据中自动发现合理且可解释的模型的重要性。随着数据量的不断增长,如何从中提取有用的信息和知识成为了机器学习领域的一大挑战。通过利用概率框架和贝叶斯推理,我们可以自动发现与数据最匹配的模型,并解释这些模型背后的含义。
最后,文章讨论了层次建模在学习多个相关模型时的应用。层次建模允许我们构建具有层次结构的模型,以捕捉不同模型之间的依赖关系和交互作用。这对于处理复杂数据和解决复杂问题具有重要意义。
2.概率模型和不确定性
2.1.不确定性
数据是机器学习系统的核心要素,然而,即使是庞大的大数据集,如果无法从中提炼出有价值的知识或推论,那么这些数据本身便显得毫无意义。几乎所有的机器学习任务本质上都可以归结为从观察到的数据中推断出那些缺失或潜在的数据——我将这些任务统称为“推断”、“预测”或“预估”。
以分类任务为例,比如我们希望通过患者的基因表达模式将白血病患者归类为该疾病的四个主要亚型之一。在此情境下,观察到的数据是基因表达模式与已知亚型的配对,而我们需要推断的则是新患者的未知亚型。为了从已有数据中推断出未知的信息,学习系统需要依据一定的假设进行工作;这些假设的集合便构成了一个模型。
模型的形式可以多样,有的简单而刚性,如传统的统计线性回归模型;有的则复杂且灵活,如庞大的深度神经网络,甚至可以是具有无限参数的模型。但无论模型如何构建,如果它不能对新数据进行有效的预测,那么这个模型就无法被证实其有效性,正如哲学家卡尔·波普尔在评估假设时所强调的那样,或者如理论物理学家沃尔夫冈·泡利所言,这样的模型是“毫无意义的”。
在建模过程中,不确定性是不可避免且至关重要的。不确定性有多种形式:在最低层次上,它可能源于测量噪声,如图像中的像素噪声或模糊;在更高级别上,模型可能包含众多参数,如线性回归中的系数,这些参数的不确定性会影响模型对新数据的预测能力;最后,在最高层次上,甚至模型的整体结构也可能存在不确定性——比如,我们是应该选择线性回归还是神经网络,如果是后者,又应该设计多少层网络结构等。
为了有效地表达和处理这些不确定性,我们采用概率建模的方法。概率论为我们提供了一种数学语言,用于描述和操作不确定性,正如微积分在处理变化率时的作用一样。幸运的是,概率建模的概念相对简单:我们使用概率分布来表示模型中所有不确定的、未观察到的变量(包括结构、参数和与噪声相关的因素),以及它们与数据之间的关系。然后,利用概率论的基本原理,我们根据观察到的数据来推断那些未观察到的变量。通过将先验概率分布(在观察数据之前定义的)转化为后验分布(在观察数据之后得到的),学习过程便得以进行。这种将概率论应用于数据学习的方法,我们称之为贝叶斯学习。
除了概念上的简洁性,概率框架在赋予机器智能方面还具有一系列引人注目的特性。这些特性使得概率建模成为了一个强大的工具,能够构建出复杂且易于理解的模型。
首先,简单的概率分布可以作为构建更大、更复杂模型的基石。在过去二十年里,图形模型成为了表示这种组合概率模型的主要范式,包括有向图(如贝叶斯网络和信念网络)、无向图(如马尔可夫网络和随机场),以及融合了有向和无向边的混合图。概率编程进一步扩展了图形模型的概念,提供了一种更加灵活和强大的方式来构建和表示概率模型。
概率模型的组合性是其另一个显著优势。通过将简单的概率分布组合在一起,我们可以构建出复杂且易于理解的模型。与将非线性动态系统(如递归神经网络)耦合在一起相比,这些构建块在更大模型中的行为通常更加直观和易于理解。特别地,一个定义良好的概率模型总是能够生成数据,这些“想象”的数据为我们提供了一个洞察模型“思想”的窗口,有助于我们理解初始的先验假设以及模型在后续阶段所学到的内容。
此外,概率建模在概念上也具有优势,因为它为人工智能系统中的学习提供了一个规范的理论框架。Cox公理定义了表示信念的一些期望属性,其中一个关键结果是,信念程度(从“不可能”到“绝对确定”)必须遵循所有概率论规则。这证明了在人工智能中使用主观贝叶斯概率表示的合理性。荷兰书定理进一步强化了这一观点,它基于一个代理的信念强度可以通过其是否愿意接受各种赔率的赌注来评估的假设。该定理指出,除非一个人工智能系统(或人类)的信念程度与概率规则一致,否则它将面临接受注定会输掉钱的赌注的风险。
由于这些和许多其他关于智能中处理不确定性原则重要性的论点的力量,贝叶斯概率建模不仅作为人工智能系统中理性的理论基础出现,而且作为人类和动物规范行为的模型出现。因此,许多研究致力于探索神经回路如何可能实现贝叶斯推理,这进一步证明了概率建模在理解和构建智能系统方面的广泛应用和重要性。
2.2.贝叶斯机器学习
概率论的基本原理,即求和规则(Sum Rule)和乘积规则(Product Rule),为我们理解不确定性提供了强大的工具。
考虑两个随机变量
x
x
x 和
y
y
y,它们分别取值于集合
X
X
X 和
Y
Y
Y。以天气为例,
x
x
x 和
y
y
y 可能分别代表剑桥和伦敦的天气状况,两者都取值于集合
X
=
Y
=
{
rainy
,
cloudy
,
sunny
}
X = Y = \{ \text{rainy}, \text{cloudy}, \text{sunny} \}
X=Y={rainy,cloudy,sunny}。
P ( x ) P(x) P(x) 表示 x x x 的概率,它可以解释为观察到特定值的频率,也可以代表关于它的主观信念。P ( x , y ) P(x, y) P(x,y) 是 x x x 和 y y y 的联合概率。P ( y ∣ x ) P(y | x) P(y∣x) 是在给定 x x x 的条件下 y y y 的概率,即条件概率。
求和规则:
P
(
x
)
=
∑
y
∈
Y
P
(
x
,
y
)
P(x)=\displaystyle\sum_{y\in{Y}}{P(x,y)}
P(x)=y∈Y∑P(x,y)
乘积规则:
P
(
x
,
y
)
=
P
(
x
)
P
(
y
∣
x
)
P(x,y)=P(x)P(y|x)
P(x,y)=P(x)P(y∣x)
求和规则(Sum Rule)表明,
x
x
x 的边际概率(Marginal Probability)可以通过对
y
y
y 的所有可能值求和(对于连续变量则是积分)联合概率
P
(
x
,
y
)
P(x, y)
P(x,y) 来得到。
乘积规则(Product Rule)则表明,联合概率
P
(
x
,
y
)
P(x, y)
P(x,y) 可以分解为边际概率
P
(
x
)
P(x)
P(x) 和条件概率
P
(
y
∣
x
)
P(y | x)
P(y∣x) 的乘积。
贝叶斯规则(Bayes’ Rule)是这两个规则的推论,它在机器学习中扮演着核心角色。在机器学习的上下文中,我们可以将
x
x
x 替换为
D
D
D,代表观察到的数据;将
y
y
y 替换为
θ
\theta
θ,代表模型的未知参数;并且根据我们正在考虑的模型类别
m
m
m 来条件化所有项。因此,贝叶斯规则在机器学习中的形式为:
P
(
y
∣
x
)
=
P
(
x
∣
y
)
P
(
y
)
P
(
x
)
=
P
(
x
∣
y
)
P
(
y
)
∑
y
∈
Y
P
(
x
,
y
)
P(y|x)=\frac{P(x|y)P(y)}{P(x)}=\frac{P(x|y)P(y)}{\displaystyle\sum_{y\in{Y}}{P(x,y)}}
P(y∣x)=P(x)P(x∣y)P(y)=y∈Y∑P(x,y)P(x∣y)P(y)
P
(
θ
∣
D
,
m
)
=
P
(
D
∣
θ
,
m
)
P
(
θ
∣
m
)
P
(
D
∣
m
)
P(\theta | D, m) = \frac{P(D | \theta, m) P(\theta | m)}{P(D | m)}
P(θ∣D,m)=P(D∣m)P(D∣θ,m)P(θ∣m)
P ( D ∣ θ , m ) P(D | \theta, m) P(D∣θ,m) 是模型 m m m 中参数 θ \theta θ 的似然性(Likelihood)。P ( θ ∣ m ) P(\theta | m) P(θ∣m) 是 θ \theta θ 的先验概率(Prior Probability),代表我们对参数的初始信念或假设。P ( θ ∣ D , m ) P(\theta | D, m) P(θ∣D,m) 是给定数据 D D D 的 θ \theta θ 的后验概率(Posterior Probability),它融合了数据中的信息和我们的先验知识。
学习过程就是通过数据
D
D
D 将先验知识或假设
P
(
θ
∣
m
)
P(\theta | m)
P(θ∣m) 转化为后验知识
P
(
θ
∣
D
,
m
)
P(\theta | D, m)
P(θ∣D,m) 的过程。这个后验概率现在成为用于预测新数据的先验概率。
使用学到的模型预测未见过的测试数据
D
test
D_{\text{test}}
Dtest 时,我们可以简单地应用求和规则和乘积规则:
P
(
D
test
∣
θ
,
m
)
=
∑
θ
P
(
D
test
∣
D
,
θ
,
m
)
P
(
θ
∣
D
,
m
)
P(D_{\text{test}} | \theta, m) = \sum_{\theta} P(D_{\text{test}} | D, \theta, m) P(\theta | D, m)
P(Dtest∣θ,m)=θ∑P(Dtest∣D,θ,m)P(θ∣D,m)
(注意:在实际应用中,通常不会直接对
θ
\theta
θ 进行求和,而是对
θ
\theta
θ 的后验分布进行采样或近似积分。)
最后,不同的模型可以通过在
m
m
m 的层次上应用贝叶斯规则来比较:
P
(
D
∣
m
)
=
∫
P
(
D
∣
θ
,
m
)
P
(
θ
∣
m
)
d
θ
P(D | m) = \int P(D | \theta, m) P(\theta | m) \, d\theta
P(D∣m)=∫P(D∣θ,m)P(θ∣m)dθ
这里的
P
(
D
∣
m
)
P(D | m)
P(D∣m) 被称为边际似然(Marginal Likelihood)或模型证据(Model Evidence),它实现了对简单模型的偏好,这被称为贝叶斯奥卡姆剃刀(Bayesian Occam’s Razor)。
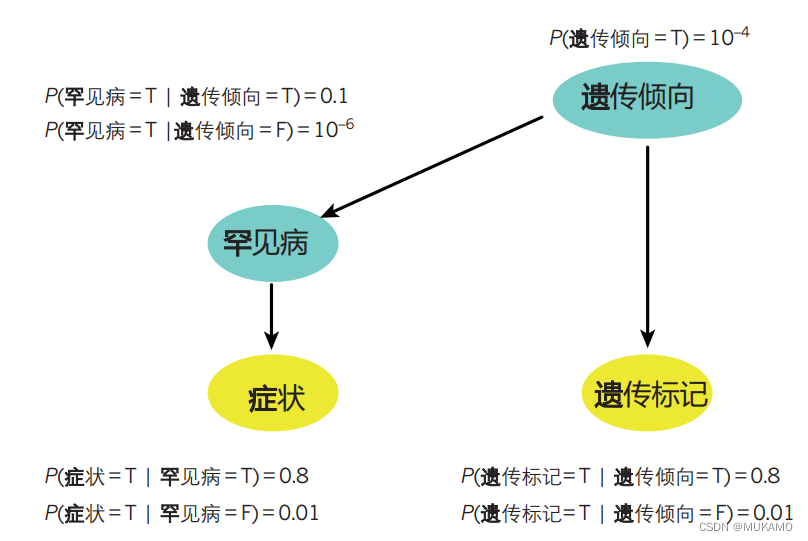
图1 | 深入解析贝叶斯推断
贝叶斯推断在医学诊断领域的应用提供了一个生动的例子。假设我们面临一个挑战:通过患者的症状和潜在的遗传标记测量结果来诊断一种罕见的疾病。在这个案例中,所有的变量都是二元的,即它们只有两种状态——真(T)或假(F)。
我们通过有向箭头来描绘变量之间的关系,并明确展示了每个变量在给定其直接依赖的其他变量条件下的概率。其中,黄色节点代表那些可以直接观察到的变量(如症状和遗传标记),而绿色节点则代表那些我们无法直接观测到但可能对诊断有重要影响的隐藏变量(如患者的遗传倾向)。
通过运用求和规则(如框1所述),我们可以计算出患者患有这种罕见疾病的先验概率。在这个例子中,这个概率是P(罕见疾病=T) = 1.1 × 10−5,它是基于患者遗传倾向的条件概率和遗传倾向本身的概率计算得出的。
然而,当我们有了更多的信息——比如患者出现了特定的症状或携带了特定的遗传标记时,我们就可以利用贝叶斯定理来更新我们对于这个罕见疾病概率的估计。具体来说,如果一个患者出现了症状,那么他患有这种罕见疾病的概率会提高到8.8 × 10−4;而如果他携带了特定的遗传标记,这个概率会变为7.9 × 10−4。
更进一步,如果我们得知患者同时出现了症状和携带了遗传标记,那么患有罕见疾病的概率会显著增加到0.06。
需要强调的是,这里所展示的是一组固定的、已知的模型参数(即θ = (10−4, 0.1, 10−6, 0.8, 0.01, 0.8, 0.01))。但在实际应用中,这些参数以及模型的结构(如箭头的存在与否和额外的隐藏变量)都可以从大量的患者记录数据集中学习得到,从而为我们提供更准确、更个性化的诊断支持。
2.3.概率模型面临的挑战
在深度学习和概率机器学习的领域中,一个显著的挑战在于计算复杂性,特别是当我们尝试精确地执行某些操作时,目前并没有已知的多项式时间算法来直接实现这些计算。然而,幸运的是,研究人员已经开发出了多种近似积分算法来应对这一难题,这些方法包括但不限于马尔可夫链蒙特卡罗(MCMC)技术、变分近似法、期望传播算法以及序列蒙特卡罗等。
当我们深入探讨贝叶斯机器学习与其他机器学习分支的区别时,会发现一个显著的计算焦点差异:对于贝叶斯研究者而言,他们面临的主要计算挑战是积分问题,而机器学习社区的大部分成员则更侧重于模型参数的优化。但值得注意的是,这种二分法并非绝对。实际上,许多基于梯度的优化方法可以通过结合郎之万蒙特卡罗和哈密顿蒙特卡罗技术转化为积分方法,同时,积分问题也可以通过变分近似法转化为优化问题。
在概率机器学习的建模过程中,一个主要挑战是确保模型具有足够的灵活性,以捕捉数据中实现特定预测任务所需的所有特性。为了应对这一挑战,一种方法是开发一个能够随数据复杂度变化而自动调整模型复杂度的先验分布。这种能够随着数据复杂性的增长而增长的灵活模型背后的关键统计概念是非参数化方法。这种方法允许模型在不需要预设固定数量的参数或模型结构的情况下,自动地适应数据的复杂性,从而更有效地捕捉数据的内在模式和规律。
3.非参数方法的优点
现代机器学习的一个显著教训是,当从大型数据集学习时,最佳的预测性能通常来自于高度灵活的学习系统。这种灵活性使得模型能够更好地“让数据自己说话”,因为它们能够在更大程度上适应数据的复杂性和特征。然而,需要明确的是,所有预测都基于一定的假设,因此数据永远不会完全“为自己说话”。
实现模型灵活性的方法主要有两种。一种是通过增加模型参数的数量,使其远远超过数据集的大小。例如,用于英法句子翻译任务的神经网络,其参数数量高达3.84亿,这种方法使模型能够接近最先进的准确度。另一种方法是使用非参数组件来定义模型。
理解非参数模型的最佳途径是将其与参数模型进行比较。在参数模型中,无论观察到多少训练数据,都只有固定且有限数量的参数需要被设定,这些参数控制未来的预测。相反,非参数模型的预测能力会随着训练数据量的增加而增强,它们要么通过一系列参数数量递增的参数模型进行嵌套,要么从具有无限多参数的模型出发。
例如,在分类问题中,线性(参数)分类器总是使用类之间的线性边界进行预测,而非参数分类器则能够学习一个非线性边界,这个边界的形状会随着更多数据的加入而变得更加复杂。许多非参数模型可以从参数模型开始,并考虑当模型参数增长到无限多时的情况。然而,将具有无限多参数的模型拟合到有限的训练数据会导致“过拟合”,即模型的预测可能反映训练数据的特定特征,而不是可以推广到测试数据的规律。
幸运的是,贝叶斯方法通过对参数进行平均而非直接拟合参数,因此它们相对不易受到过拟合的影响。此外,对于许多应用来说,我们拥有庞大的数据集,因此主要关注的是选择过于简单化的参数模型导致的欠拟合问题,而不是过拟合。
虽然贝叶斯非参数的完整讨论超出了这篇综述的范围,但值得提及一些关键模型。高斯过程是一种对未知函数非常灵活的非参数模型,广泛应用于回归、分类以及需要对函数进行推断的其他应用。例如,在化学领域,我们可能需要学习一种化学物质剂量与生物体反应之间的函数关系。使用高斯过程,我们可以直接学习与数据一致的非参数非线性函数的分布,而不是使用线性参数函数来模拟这种关系。高斯过程的一个著名应用案例是GaussianFace,这是一种先进的面部识别方法,其性能甚至超过了人类和某些深度学习方法。
狄利克雷过程(Dirichlet Process, DP)作为统计学中历史悠久的非参数模型,其应用广泛,涵盖了密度估计、聚类、时间序列分析和文档主题建模等多个领域。以狄利克雷过程为例,当将其应用于社交网络中的友谊建模时,它允许我们构建一种模型,其中推断出的社区(即聚类)数量能够随着人数的增加而自然增长。这种特性使得狄利克雷过程成为分析社交网络结构的有力工具。此外,狄利克雷过程也已在聚类基因表达模式等领域展现出其强大的能力。
印度自助餐过程(Indian Buffet Process, IBP)是另一种非参数模型,它主要用于潜在特征建模、学习重叠聚类、稀疏矩阵分解以及非参数方式下的深度网络结构学习。在社交网络建模的情境中,基于IBP的模型允许每个人属于多个潜在社区的子集(这些社区可能由不同的家庭、工作场所、学校、爱好等定义)。友谊的概率则依赖于两人所拥有的重叠社区的数量。在这个框架中,每个人的潜在特征对应于那些未直接观察到的社区。IBP可以被视为一种为贝叶斯非参数模型赋予“分布式表示”的方法,这与神经网络文献中流行的概念相呼应。
贝叶斯非参数模型和神经网络之间的联系颇为有趣。在特定条件下,具有无限多隐藏单元的神经网络实际上等同于高斯过程。这意味着,这两种看似不同的建模方法在某些情况下可以相互转化,共享相似的建模能力和灵活性。
非参数组件,如狄利克雷过程和印度自助餐过程,应被视为构建复杂模型的强大构建块。它们可以像前面描述的那样组合起来,形成更高级、更强大的模型。下一节将探讨一种更强大的模型组合方式——概率编程,它允许我们以更加直观和灵活的方式构建和表达复杂的统计模型。
4.概率编程
4.1.概率编程示例
# 发射参数(Emission parameters),即每个状态对应的观测值均值
statesmean =[-1,1,0]
# 初始状态的概率分布,即初始时每个状态的概率都是1/3
initial =Categorical([1.0/3,1.0/3,1.0/3])
# 每个状态的转移概率分布
# 状态1转移到其他状态的概率
trans =[Categorical([0.1,0.5,0.4]), # 从状态1转移到状态1,2,3的概率
Categorical([0.2,0.2,0.6]), # 从状态2转移到状态1,2,3的概率
Categorical([0.15,0.15,0.7]) # 从状态3转移到状态1,2,3的概率
]
# 观测数据,其中Nil可能表示缺失数据或起始标记
data =[Nil,0.9,0.8,0.7,0,-0.025,-5,-2,-0.1,0,0.13]
# 定义一个名为hmm的模型
@model hmm begin
# 定义一个整数数组states,长度与data相同,用于存储每个时刻的隐藏状态
states =Array(Int,length(data))
# 假设第一个状态服从初始概率分布
@assume(states[1] ~ initial)
# 对数据中的每个观测值(从第二个开始)
for i =2:length(data)
# 假设当前状态基于前一个状态的转移概率分布
@assume(states[i] ~ trans[states[i-1]])
# 观测数据data[i]服从以当前状态对应的均值和固定方差(0.4)的正态分布
# 注意:如果data[i]是Nil,则此观察操作将不会执行
if data[i]!= Nil
@observe(data[i] ~ Normal(statesmean[states[i]],0.4))
end
end
# 预测(或推断)隐藏状态数组states
@predict states
end
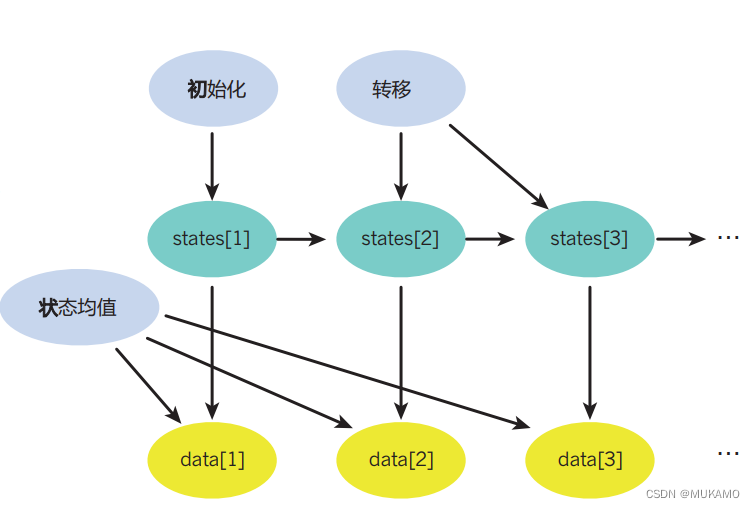
图2 | 深度解读概率编程
左侧:在Julia编程语言中定义了一个简洁但功能强大的三状态隐马尔可夫模型(HMM)。这个模型受到了文献中广泛认可示例的启发,展现了概率编程在建模序列和时间序列数据时的强大能力。HMM的基本假设是,观测到的数据是通过一系列隐藏状态之间的随机转移生成的。
模型参数与数据:
trans:一个3x3的矩阵,定义了不同隐藏状态之间的转移概率。initial:初始状态下每个隐藏状态的概率分布。statesmean:每个隐藏状态对应的观测均值,实际观测值则是这些均值加上高斯噪声的扰动。
hmm函数:该函数定义了HMM的核心逻辑。通过
@assume
语句,我们为隐藏状态序列的生成建立了概率模型。
@observe
语句则将模型与实际的观测数据关联起来,实现了条件概率的建模。最后,
@predict
语句表明我们希望通过这个模型来推断隐藏状态及未观测的数据。这一切都由强大的通用推理引擎自动完成,该引擎可以基于模型的配置进行复杂的概率推理。
右侧:对应的图形模型直观地展示了模型的结构和变量间的依赖关系。蓝色代表参数,绿色代表隐藏状态变量,黄色代表观测数据。这个图形模型清晰地反映了概率模型的组合性质,即模型是由多个相互依赖的组件构成的,每个组件都贡献了一部分概率信息。
通过深度解读这个概率编程示例,我们可以看到概率编程在构建复杂概率模型、处理序列数据以及进行概率推理方面的强大能力。这种能力使得概率编程在机器学习、数据分析和人工智能等领域具有广泛的应用前景。
4.2.概率编程理论
概率编程的核心思想在于利用计算机程序来精确描述和表示概率模型。一种实现方式是通过创建模拟器,这些模拟器作为生成器从概率模型中抽取数据。模拟器内部使用随机数生成器,确保每次运行模拟器时都能从模型中采样出不同的可能数据集。这种模拟框架相较于图形模型框架具有更高的通用性,因为它允许使用递归和控制流语句(如“if”语句),这些在图形模型中可能难以直观表达。
实际上,基于扩展图灵完备语言的现代概率编程语言,包括大多数常用的编程语言,可以表示任何可计算的概率分布作为概率程序。这种灵活性使得概率编程成为一种强大的工具,用于描述和模拟复杂的概率系统。
概率编程的真正价值在于它能够自动化根据观察数据推断未观察变量的过程。从概念上讲,这涉及到逆向推理:给定程序的输出(即观察到的数据),需要确定程序输入状态(特别是随机数生成器的调用)以匹配这些输出。尽管我们通常习惯于从输入到输出的正向执行程序,但概率编程中的条件化涉及解决一个逆向问题,即寻找导致特定输出的输入。
这种条件化过程通常由“通用推理引擎”执行,它采用蒙特卡洛抽样方法,在与观察数据一致的模拟器程序的可能执行上进行。这种推理算法的实现对于计算机程序而言是可行的,这在某种程度上是令人瞩目的,但这也反映了采样思想的普遍性和有效性,如拒绝采样、顺序蒙特卡洛方法和“近似贝叶斯计算”等技术的广泛应用。这些技术共同构成了概率编程的基础,使得从复杂的概率模型中提取有用信息成为可能。
举例来说,假设你开发了一个概率程序,该程序模拟了一个复杂的基因调控网络。在这个网络中,未测量的转录因子与特定基因的表达水平之间存在潜在的关联。模型中的不确定性通过模拟器内部的各种概率分布来量化。随后,借助通用推理引擎,你可以根据实验测量的基因表达水平来条件化这个模拟器的输出,从而自动推断出那些未测量的转录因子以及其他未知的模型参数的活动状态。
概率编程的另一个引人注目的应用是在计算机视觉领域,它将复杂的图像分析任务视为图形渲染过程的逆过程。通过模拟图像生成的过程,概率编程可以帮助计算机理解图像中对象的结构、姿态和光照条件。
概率编程之所以可能对机器智能和科学建模产生深远影响,原因有多方面。首先,通用推理引擎的引入极大地减少了手动推导和实现模型推理方法的需求。这一步骤在建模过程中往往耗时且容易出错,而自动化这一过程可以显著加速机器学习系统的开发周期,将原本可能需要数月的工作缩短至几分钟或几秒钟。
其次,概率编程为科学研究和探索提供了前所未有的灵活性。它允许研究者快速构建和测试不同的数据模型,从而加速科学发现的过程。此外,概率编程语言在模型和推理程序之间建立了清晰的界限,鼓励研究者从模型驱动的角度出发,更加深入地理解问题的本质。
目前,市面上存在多种概率编程语言,如BUGS、Stan、AutoBayes和Infer.NET等。这些语言在表达能力和通用性上各有千秋,但相较于基于图灵完备语言的系统(如IBAL、BLOG、Church、Figaro、Venture和Anglican),它们通常只能表示受限类别的模型。然而,这种限制使得这些语言在推理速度上往往具有显著优势。
尽管大多数概率编程方法都基于贝叶斯框架,但也有一些例外,如Theano这样的系统。Theano本身并非概率编程语言,但它通过符号微分技术加速了神经网络和其他概率模型参数的优化过程。尽管参数优化是改进概率模型的重要工具,但最近的研究也在探索如何利用概率建模来改进优化算法,这一领域的发展将为我们提供更强大的工具来解决复杂的不确定性问题。
5.贝叶斯优化
5.1.贝叶斯优化图解
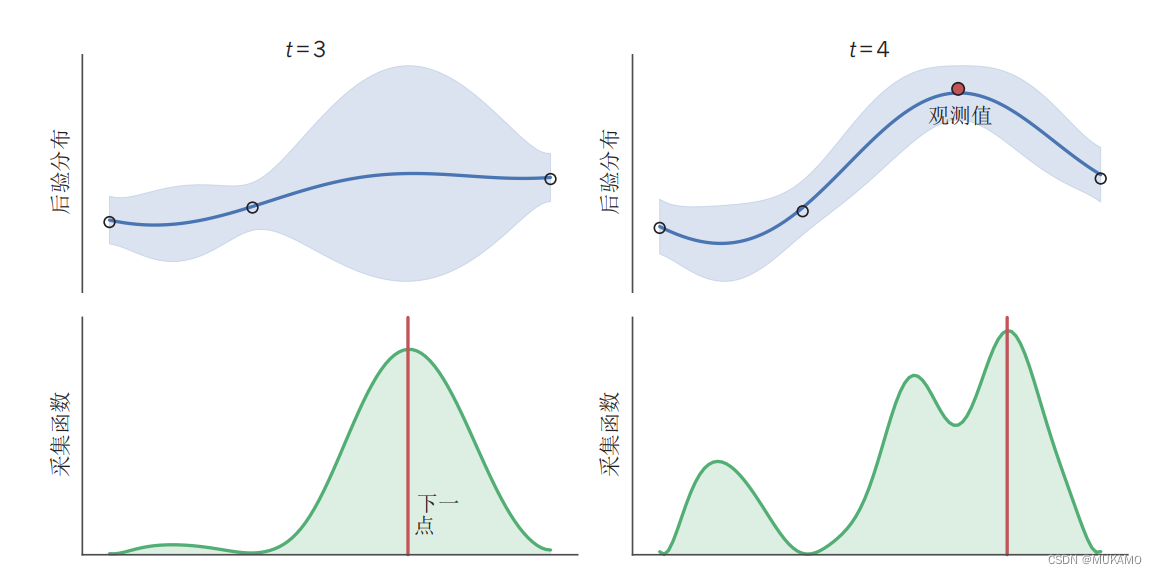
图3 | 深度解读贝叶斯优化
贝叶斯优化是一种强大的优化技术,特别适用于那些函数形式未知、计算成本高昂或者难以直接计算梯度的场景。在图中,我们展示了贝叶斯优化在一维空间中的工作原理。我们的目标是最大化某个未知的真实函数f,该函数的具体形式在图中并未直接显示。
5.1.1.过程解析:
- 数据收集:通过选择特定的x值来评估函数f,并将这些评估结果(以圆圈的形式在图中表示)作为观测值。
- 后验推断:基于这些观测值,我们可以推断出函数f的可能取值范围的后验分布。这个后验分布用蓝色线条表示均值,蓝色阴影区域则表示标准差,即不确定性。请注意,随着x值远离观测点,不确定性会逐渐增大。
- 获取函数:基于函数f的后验分布,我们可以计算出一个获取函数(在图中以绿色阴影区域表示)。这个获取函数衡量了在不同x值处评估函数f的预期增益。通常,当f的后验均值较高且不确定性较大时,获取函数的值也会较高。这是因为在这些区域,我们既有理由相信函数值可能很高,又有足够的探索空间来发现更好的解。
- 决策制定:获取函数的峰值(以红线表示)指出了下一个最值得评估的x值。因此,我们选择这个x值进行新的评估(以红色圆圈表示),并更新我们的后验分布和获取函数。
5.1.2.示例演化:
- 左图:展示了在进行了三次函数评估后的情况。可以看到,随着观测点的增加,后验分布逐渐变得更加精确,而获取函数也指向了更有可能找到函数最大值的区域。
- 右图:在进行了第四次评估后,我们可以看到后验分布和获取函数都进一步得到了更新。这种迭代的过程会持续进行,直到我们达到满意的解或者评估预算耗尽为止。
通过深度解读贝叶斯优化的工作原理,我们可以看到它是一种灵活而强大的优化方法,特别适用于那些传统优化方法难以处理的复杂场景。通过不断地进行函数评估和后验推断,贝叶斯优化能够在有限的评估预算内有效地探索搜索空间,从而找到函数的近似最优解。
5.2. 贝叶斯优化
贝叶斯优化是一种先进的序列决策方法,专门用于解决在昂贵评估代价下寻找未知函数全局最大值的问题。在数学上,给定一个定义在域
X
X
X上的函数f,贝叶斯优化的目标是找到该函数的全局最大化器
x
∗
x^*
x∗,即:
x
∗
=
arg
max
x
∈
X
f
(
x
)
x^* = \displaystyle\arg\max_{x \in X} f(x)
x∗=argx∈Xmaxf(x)
贝叶斯优化方法的核心在于如何高效地最大化f,同时充分考虑到从已有观测中获取的对未知函数f的信息增益。假设我们已经在三个点进行了评估,并得到了相应的函数值
[
(
x
1
,
f
(
x
1
)
)
,
(
x
2
,
f
(
x
2
)
)
,
(
x
3
,
f
(
x
3
)
)
]
[(x_1, f(x_1)), (x_2, f(x_2)), (x_3, f(x_3))]
[(x1,f(x1)),(x2,f(x2)),(x3,f(x3))],贝叶斯优化算法会基于这些信息来决定下一步应该评估哪个点
x
x
x,并预测最大值可能位于何处。
这一问题在机器智能领域具有重要的实际意义,因为它广泛应用于科学与工程的多个领域,如药物设计(函数代表药物的效力)和机器人技术(函数代表机器人步态的速度)。贝叶斯优化尤其适用于任何涉及昂贵函数评估的问题,这里的“昂贵”指的是函数评估可能消耗大量的计算资源,因此需要在优化过程中进行权衡。
目前,表现最佳的全局优化方法通常维护一个贝叶斯表示,即关于正在优化的不确定函数f的概率分布。这种不确定性被用来指导优化算法决定下一步的查询位置。在连续空间中,大多数贝叶斯优化方法采用高斯过程来模拟未知函数。最近,贝叶斯优化在优化机器学习模型(包括深度神经网络)的训练过程方面取得了显著成果,这进一步展示了其强大的应用潜力。
此外,贝叶斯优化与强化学习之间存在有趣的联系。贝叶斯优化可以看作是一个无状态的序列决策问题,即决策(选择要评估的点
x
x
x)不会改变系统的状态(实际的函数
f
f
f)。这类问题属于多臂老虎机问题,是强化学习的一个子类。更广泛地说,贝叶斯方法正在被用于学习控制不确定系统,其中准确表示行动未来结果的不确定性对于做出明智的决策至关重要。良好的决策往往需要依赖于不同结果及其相对收益的概率的精确表示。
贝叶斯优化作为贝叶斯数值计算的一个特例,正在成为一个非常活跃的研究领域,它利用概率论来量化计算过程中的不确定性,并在各种优化问题中展现出强大的应用前景。
6.数据压缩
数据压缩是信息技术中不可或缺的一环,它致力于以最少的位数来存储或传输数据,同时确保原始数据可以完全恢复。这种无损数据压缩技术在现代社会的各个角落都发挥着重要作用,从个人电脑的硬盘存储到互联网上的海量数据传输。数据压缩与概率建模之间存在着密不可分的关系,两者互为表里,相互促进。
贝叶斯机器学习方法的兴起为数据压缩技术带来了新的突破。它基于一个核心观点:更准确的概率模型能够带来更高的压缩率。这是因为压缩的本质在于去除数据中的冗余信息,而概率模型则能够揭示数据中的统计规律和模式,从而指导我们如何更有效地去除这些冗余。
随着贝叶斯机器学习技术的不断发展,我们有能力构建更加灵活和自适应的概率模型。这是因为不同类型的数据序列往往具有非常不同的统计特征,例如莎士比亚的戏剧文本和计算机源代码就有着截然不同的语言结构和模式。一些世界领先的压缩算法,如Sequence Memoizer和具有动态参数更新的PPM,实际上就是序列数据的贝叶斯非参数模型。这些算法通过深入理解序列的统计结构,不断优化压缩性能。
展望未来,随着概率机器学习技术的不断进步,我们有望看到更多针对非序列数据(如图像、图形和其他结构化对象)的特定压缩方法涌现。这些新的压缩方法将能够更好地捕捉数据的内在规律和模式,从而实现更高的压缩率和更好的恢复质量。因此,我们可以期待在不久的将来,数据压缩技术将在信息技术领域发挥更加重要的作用,为我们带来更加高效、便捷的数据存储和传输体验。
7.数据主动建模
7.1.主动统计建模示例
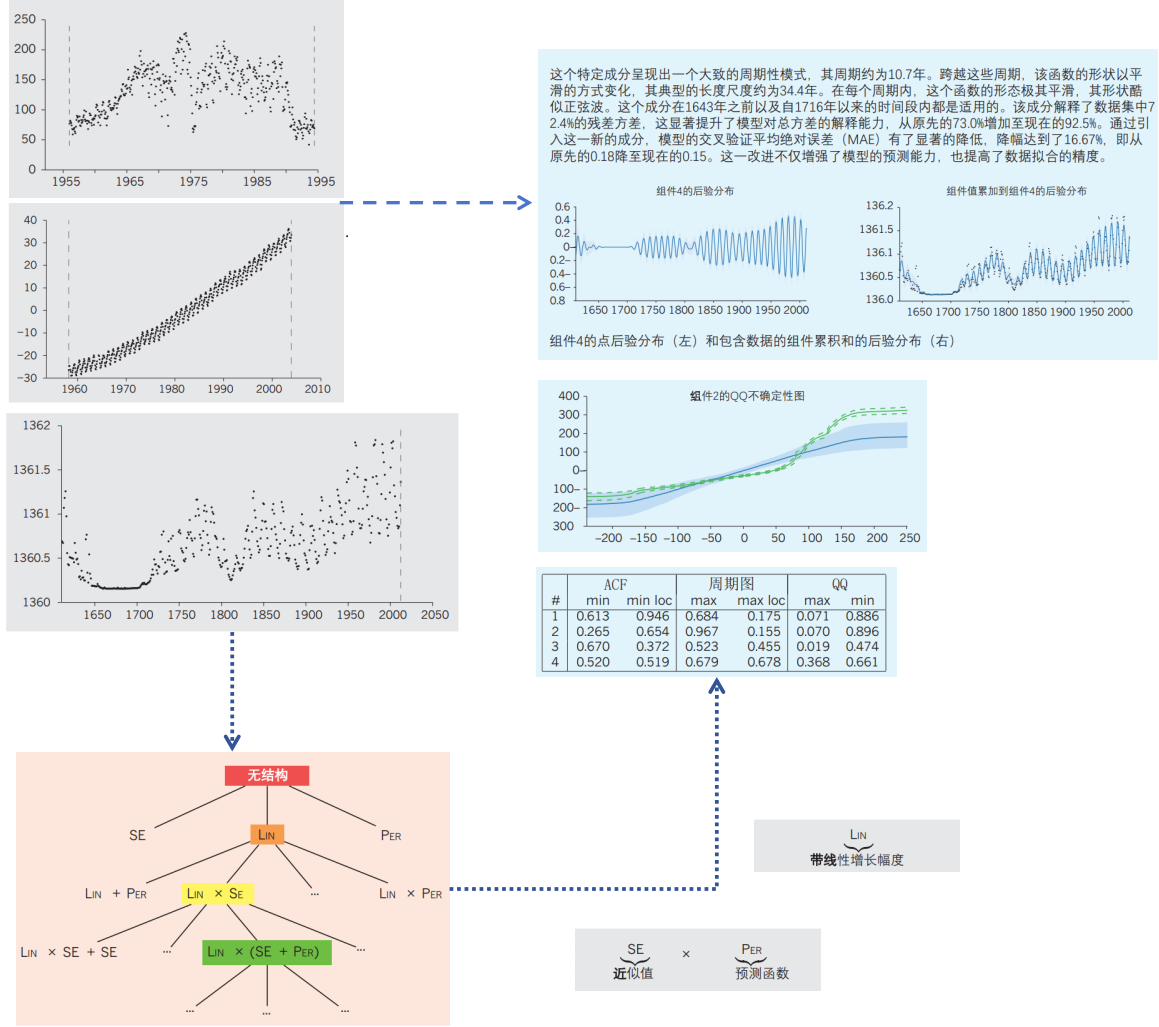
图4 | 自动统计建模
自动统计学家是一个高级数据分析工具,它通过一系列步骤自动地处理和分析数据。首先,它接收数据作为输入,这些数据通常以时间序列的形式呈现(如左上图所示)。接下来,系统启动其核心功能:通过遍历一组预设的模型语法,自动寻找最能准确解释输入数据的模型(如左下图所示)。这一过程中,自动统计学家采用了贝叶斯推断来对各个模型进行评分和选择。
一旦系统确定了最佳模型,它会将这些模型的组成部分转化为易于理解的英文描述(如右下图所示)。这不仅包括模型的核心结构和参数,还可能包括一些对模型特性的直观解释。
最后,自动统计学家会生成一份详尽的报告(如右上图所示),这份报告以文本、图表和表格的形式,详细阐述了从数据中推断出的信息。这份报告不仅涵盖了数据的基本统计特征,还包括了模型检验和评估的部分,帮助用户更全面地理解数据和模型的有效性。
需要注意的是,图中的数据和报告仅为示例,用于说明自动统计学家的工作流程和输出成果。在实际应用中,自动统计学家可以根据具体的数据和需求,生成具有针对性的分析和报告。
7.2.主动模型的进展
在数据科学领域,自动发现可解释模型一直是一个引人瞩目的挑战。自动统计学家(Automatic Statistician)的设想正是为了解决这一难题,它旨在无需人工干预就能从数据中自动挖掘出合理的模型,并以清晰易懂的英语向用户解释这些发现。这种能力对于任何需要从数据中提炼知识的领域都极具价值。
与传统的机器学习技术相比,自动统计学家不仅仅追求在模式识别任务上取得微小的性能提升,而是更注重构建由可解释组件组成的模型,并且能够系统地处理模型结构的不确定性。无论数据集的大小,它都能提供合理且有用的答案。特别地,贝叶斯方法为自动统计学家提供了优雅的工具,用以在模型的复杂性和数据的复杂性之间找到最佳的平衡点。通过概率模型的组合,它不仅能解释数据中的规律,还能提供这些规律背后的不确定性。
自动统计学家的原型版本已经能够处理时间序列数据,并自动生成详尽的报告,详细描述了它所发现的模型。这一系统的核心思想在于,通过灵活的语法将概率构建块组合在一起,构建出一个开放而强大的模型语言。与传统的方程学习方法不同,自动统计学家关注的是捕捉函数的一般特性,如平滑性、周期性或趋势,而不仅仅是寻找一个精确的公式。
在自动统计学家的设计中,处理不确定性是一个至关重要的环节。它利用贝叶斯非参数方法提供足够的灵活性,以实现卓越的预测性能,并通过边际似然度量来智能地搜索模型空间。这一领域的重要先驱包括统计专家系统和机器人科学家,它们已经成功地将机器学习和科学发现与实验设计和执行自动化相结合。最近,Auto-WEKA 项目也展现了自动化学习分类器过程的潜力,它充分利用了贝叶斯优化技术。
随着技术的不断进步,自动应用机器学习方法到数据中的努力正日益增强。未来,我们有望看到更加智能的数据科学人工智能系统,它们将能够自动发现、解释并应用从数据中提取的知识。
8.展望
在信息革命的时代背景下,大数据集的可用性日益增长,为建模提供了前所未有的机会。然而,面对这些数据海洋,不确定性在建模过程中仍然扮演着不可忽视的角色。尽管经典统计理论表明,在特定条件下,大数据集下贝叶斯参数模型的参数后验分布会趋于稳定,但这并不意味着在大数据面前,贝叶斯概率建模的不确定性就变得无关紧要。
实际上,有两个关键原因说明不确定性在大数据建模中依然重要。首先,贝叶斯非参数模型由于其本质上的无限参数特性,使得它们的学习能力不会因数据量的大小而饱和,预测性能可以持续优化。其次,很多看似庞大的数据集实际上是由众多小型数据集构成的集合。在个性化医疗和推荐系统等领域,尽管总体数据量庞大,但具体到每个患者或客户,数据仍然相对有限。为每个人定制预测模型,就需要为每个人构建一个带有其独特不确定性的模型,并通过层次结构将这些模型耦合在一起,以从其他类似个体中借鉴信息。这种模型的个性化,正是通过如层次狄利克雷过程和贝叶斯多任务学习等层次贝叶斯方法来实现的。
机器学习和智能的概率方法是一个充满活力的研究领域,其影响远超传统的模式识别范畴。从数据压缩、优化、决策制定,到科学模型的发现和解释,再到个性化服务,概率方法都发挥着至关重要的作用。区分概率方法重要性的关键在于不确定性是否成为问题的核心。此外,许多传统的基于优化的机器学习方法都有其概率类似物,这些类似物在处理不确定性时更具原则性。例如,贝叶斯神经网络能够表示神经网络中参数的不确定性,而混合模型则是聚类方法的概率对应物。
尽管概率机器学习在理论上为解决问题提供了强有力的框架,但如何在实践中以高效的方式实现这些理论方法,是该领域面临的主要挑战。幸运的是,现代推理技术的发展使得对百万级数据点进行概率建模变得可能,使得概率方法在计算上与常规方法具备了竞争力。最终,智能的核心在于在感知不完全和不确定的世界中做出理解和行动。因此,概率建模将继续在构建越来越强大的机器学习和人工智能系统中发挥核心作用。
参考文献
- Russell, S. & Norvig, P. Artificial Intelligence: a Modern Approach (Prentice–Hall, 1995).
- Thrun, S., Burgard, W. & Fox, D. Probabilistic Robotics (MIT Press, 2006).
- Bishop, C. M. Pattern Recognition and Machine Learning (Springer, 2006).
- Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT Press, 2012).
- Hinton, G. et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process. Mag. 29, 82–97 (2012).
- Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. In Proc. Advances in Neural Information Processing Systems 25 1097–1105 (2012).
- Sermanet, P. et al. Overfeat: integrated recognition, localization and detection using convolutional networks. In Proc. International Conference on Learning Representations http://arxiv.org/abs/1312.6229 (2014).
- Bengio, Y., Ducharme, R., Vincent, P. & Janvin, C. A neural probabilistic language model. J. Mach. Learn. Res. 3, 1137–1155 (2003).
- Ghahramani, Z. Bayesian nonparametrics and the probabilistic approach to modelling. Phil. Trans. R. Soc. A 371, 20110553 (2013). A review of Bayesian non-parametric modelling written for a general scientific audience.
- Jaynes, E. T. Probability Theory: the Logic of Science (Cambridge Univ. Press, 2003).
- Koller, D. & Friedman, N. Probabilistic Graphical Models: Principles and Techniques (MIT Press, 2009). This is an encyclopaedic text on probabilistic graphical models spanning many key topics.
- Cox, R. T. The Algebra of Probable Inference (Johns Hopkins Univ. Press, 1961).
- Van Horn, K. S. Constructing a logic of plausible inference: a guide to Cox’s theorem. Int. J. Approx. Reason. 34, 3–24 (2003).
- De Finetti, B. La prévision: ses lois logiques, ses sources subjectives. In Annales de l’institut Henri Poincaré [in French] 7, 1–68 (1937).
- Knill, D. & Richards, W. Perception as Bayesian inference (Cambridge Univ. Press, 1996).
- Griffiths, T. L. & Tenenbaum, J. B. Optimal predictions in everyday cognition. Psychol. Sci. 17, 767–773 (2006).
- Wolpert, D. M., Ghahramani, Z. & Jordan, M. I. An internal model for sensorimotor integration. Science 269, 1880–1882 (1995).
- Tenenbaum, J. B., Kemp, C., Griffiths, T. L. & Goodman, N. D. How to grow a mind: statistics, structure, and abstraction. Science 331, 1279–1285 (2011).
- Marcus, G. F. & Davis, E. How robust are probabilistic models of higher-level cognition? Psychol. Sci. 24, 2351–2360 (2013).
- Goodman, N. D. et al. Relevant and robust a response to Marcus and Davis (2013). Psychol. Sci. 26, 539–541 (2015).
- Doya, K., Ishii, S., Pouget, A. & Rao, R. P. N. Bayesian Brain: Probabilistic Approaches to Neural Coding (MIT Press, 2007).
- Deneve, S. Bayesian spiking neurons I: inference. Neural Comput. 20, 91–117 (2008).
- Neal, R. M. Probabilistic Inference Using Markov Chain Monte Carlo Methods. Report No. CRG-TR-93–1 http://www.cs.toronto.edu/~radford/review.abstract. html (Univ. Toronto, 1993).
- Jordan, M., Ghahramani, Z., Jaakkola, T. & Saul, L. An introduction to variational methods in graphical models. Mach. Learn. 37, 183–233 (1999).
- Doucet, A., de Freitas, J. F. G. & Gordon, N. J. Sequential Monte Carlo Methods in Practice (Springer, 2000).
- Minka, T. P. Expectation propagation for approximate Bayesian inference. In Proc. Uncertainty in Artificial Intelligence 17 362–369 (2001).
- Neal, R. M. In Handbook of Markov Chain Monte Carlo (eds Brooks, S., Gelman, A., Jones, G. & Meng, X.-L.) (Chapman & Hall/CRC, 2010).
- Girolami, M. & Calderhead, B. Riemann manifold Langevin and Hamiltonian Monte Carlo methods. J. R. Stat. Soc. Series B Stat. Methodol. 73, 123–214 (2011).
- Sutskever, I., Vinyals, O. & Le, Q. V. Sequence to sequence learning with neural networks. In Proc. Advances in Neural Information Processing Systems 27, 3104–3112 (2014).
- Neal, R. M. in Maximum Entropy and Bayesian Methods 197–211 (Springer, 1992).
- Orbanz, P. & Teh, Y. W. in Encyclopedia of Machine Learning 81–89 (Springer, 2010).
- Hjort, N., Holmes, C., Müller, P. & Walker, S. (eds). Bayesian Nonparametrics (Cambridge Univ. Press, 2010).
- Rasmussen, C. E. & Williams, C. K. I. Gaussian Processes for Machine Learning (MIT Press, 2006). This is a classic monograph on Gaussian processes, relating them to kernel methods and other areas of machine learning.
- Lu, C. & Tang, X. Surpassing human-level face verification performance on LFW with GaussianFace. In Proc. 29th AAAI Conference on Artificial Intelligence http:// arxiv.org/abs/1404.3840 (2015).
- Ferguson, T. S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1, 209–230 (1973).
- Teh, Y. W., Jordan, M. I., Beal, M. J. & Blei, D. M. Hierarchical Dirichlet processes. J. Am. Stat. Assoc. 101, 1566–1581 (2006).
- Kemp, C., Tenenbaum, J. B., Griffiths, T. L., Yamada, T. & Ueda, N. Learning systems of concepts with an infinite relational model. In Proc. 21st National Conference on Artificial Intelligence 381–388 (2006).
- Medvedovic, M. & Sivaganesan, S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics 18, 1194–1206 (2002).
- Rasmussen, C. E., De la Cruz, B. J., Ghahramani, Z. & Wild, D. L. Modeling and visualizing uncertainty in gene expression clusters using Dirichlet process mixtures. Trans. Comput. Biol. Bioinform. 6, 615–628 (2009).
- Griffiths, T. L. & Ghahramani, Z. The Indian buffet process: an introduction and review. J. Mach. Learn. Res. 12, 1185–1224 (2011). This article introduced a new class of Bayesian non-parametric models for latent feature modelling.
- Adams, R. P., Wallach, H. & Ghahramani, Z. Learning the structure of deep sparse graphical models. In Proc. 13th International Conference on Artificial Intelligence and Statistics (eds Teh, Y. W. & Titterington, M.) 1–8 (2010).
- Miller, K., Jordan, M. I. & Griffiths, T. L. Nonparametric latent feature models for link prediction. In Proc. Advances in Neural Information Processing Systems 1276–1284 (2009).
- Hinton, G. E., McClelland, J. L. & Rumelhart, D. E. in Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations 77–109 (MIT Press, 1986).
- Neal, R. M. Bayesian Learning for Neural Networks (Springer, 1996). This text derived MCMC-based Bayesian inference in neural networks and drew important links to Gaussian processes.
- Koller, D., McAllester, D. & Pfeffer, A. Effective Bayesian inference for stochastic programs. In Proc. 14th National Conference on Artificial Intelligence 740–747 (1997).
- Goodman, N. D. & Stuhlmüller, A. The Design and Implementation of Probabilistic Programming Languages. Available at http://dippl.org (2015).
- Pfeffer, A. Practical Probabilistic Programming (Manning, 2015).
- Freer, C., Roy, D. & Tenenbaum, J. B. in Turing’s Legacy (ed. Downey, R.) 195–252 (2014).
- Marjoram, P., Molitor, J., Plagnol, V. & Tavaré, S. Markov chain Monte Carlo without likelihoods. Proc. Natl Acad. Sci. USA 100, 15324–15328 (2003).
- Mansinghka, V., Kulkarni, T. D., Perov, Y. N. & Tenenbaum, J. Approximate Bayesian image interpretation using generative probabilistic graphics programs. In Proc. Advances in Neural Information Processing Systems 26 1520–1528 (2013).
- Bishop, C. M. Model-based machine learning. Phil. Trans. R. Soc. A 371, 20120222 (2013). This article is a very clear tutorial exposition of probabilistic modelling.
- Lunn, D. J., Thomas, A., Best, N. & Spiegelhalter, D. WinBUGS — a Bayesian modelling framework: concepts, structure, and extensibility. Stat. Comput. 10, 325–337 (2000). This reports an early probabilistic programming framework widely used in statistics.
- Stan Development Team. Stan Modeling Language Users Guide and Reference Manual, Version 2.5.0. http://mc-stan.org/ (2014).
- Fischer, B. & Schumann, J. AutoBayes: a system for generating data analysis programs from statistical models. J. Funct. Program. 13, 483–508 (2003).
- Minka, T. P., Winn, J. M., Guiver, J. P. & Knowles, D. A. Infer.NET 2.4. http:// research.microsoft.com/infernet (Microsoft Research, 2010).
- Wingate, D., Stuhlmüller, A. & Goodman, N. D. Lightweight implementations of probabilistic programming languages via transformational compilation. In Proc. International Conference on Artificial Intelligence and Statistics 770–778 (2011).
- Pfeffer, A. IBAL: a probabilistic rational programming language. In Proc. International Joint Conference on Artificial Intelligence 733–740 (2001).
- Milch, B. et al. BLOG: probabilistic models with unknown objects. In Proc. 19th International Joint Conference on Artificial Intelligence 1352–1359 (2005).
- Goodman, N., Mansinghka, V., Roy, D., Bonawitz, K. & Tenenbaum, J. Church: a language for generative models. In Proc. Uncertainty in Artificial Intelligence 22 23 (2008). This is an influential paper introducing the Turing-complete probabilistic programming language Church.
- Pfeffer, A. Figaro: An Object-Oriented Probabilistic Programming Language. Tech. Rep. (Charles River Analytics, 2009).
- Mansinghka, V., Selsam, D. & Perov, Y. Venture: a higher-order probabilistic programming platform with programmable inference. Preprint at http://arxiv. org/abs/1404.0099 (2014).
- Wood, F., van de Meent, J. W. & Mansinghka, V. A new approach to probabilistic programming inference. In Proc. 17th International Conference on Artificial Intelligence and Statistics 1024–1032 (2014).
- Li, L., Wu, Y. & Russell, S. J. SWIFT: Compiled Inference for Probabilistic Programs. Report No. UCB/EECS-2015–12 (Univ. California, Berkeley, 2015).
- Bergstra, J. et al. Theano: a CPU and GPU math expression compiler. In Proc. 9th Python in Science Conference http://conference.scipy.org/proceedings/ scipy2010/ (2010).
- Kushner, H. A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise. J. Basic Eng. 86, 97–106 (1964).
- Jones, D. R., Schonlau, M. & Welch, W. J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 13, 455–492 (1998).
- Brochu, E., Cora, V. M. & de Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. Preprint at http://arXiv.org/ abs/1012.2599 (2010).
- Hennig, P. & Schuler, C. J. Entropy search for information-efficient global optimization. J. Mach. Learn. Res. 13, 1809–1837 (2012).
- Hernández-Lobato, J. M., Hoffman, M. W. & Ghahramani, Z. Predictive entropy search for efficient global optimization of black-box functions. In Proc. Advances in Neural Information Processing Systems 918–926 (2014).
- Snoek, J., Larochelle, H. & Adams, R. P. Practical Bayesian optimization of machine learning algorithms. In Proc. Advances in Neural Information Processing Systems 2960–2968 (2012).
- Thornton, C., Hutter, F., Hoos, H. H. & Leyton-Brown, K. Auto-WEKA: combined selection and hyperparameter optimization of classification algorithms. In Proc. 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 847–855 (2013).
- Robbins, H. Some aspects of the sequential design of experiments. Bull. Amer. Math. Soc. 55, 527–535 (1952).
- Deisenroth, M. P. & Rasmussen, C. E. PILCO: a model-based and data-efficient approach to policy search. In Proc. 28th International Conference on Machine Learning 465–472 (2011).
- Poupart, P. in Encyclopedia of Machine Learning 90–93 (Springer, 2010).
- Diaconis, P. in Statistical Decision Theory and Related Topics IV 163–175 (Springer, 1988).
- O’Hagan, A. Bayes-Hermite quadrature. J. Statist. Plann. Inference 29, 245–260 (1991).
- Shannon, C. & Weaver, W. The Mathematical Theory of Communication (Univ. Illinois Press, 1949).
- MacKay, D. J. C. Information Theory, Inference, and Learning Algorithms (Cambridge Univ. Press, 2003).
- Wood, F., Gasthaus, J., Archambeau, C., James, L. & Teh, Y. W. The sequence memoizer. Commun. ACM 54, 91–98 (2011). This article derives a state-of-the-art data compression scheme based on Bayesian nonparametric models.
- Steinruecken, C., Ghahramani, Z. & MacKay, D. J. C. Improving PPM with dynamic parameter updates. In Proc. Data Compression Conference (in the press).
- Lloyd, J. R., Duvenaud, D., Grosse, R., Tenenbaum, J. B. & Ghahramani, Z. Automatic construction and natural-language description of nonparametric regression models. In Proc. 28th AAAI Conference on Artificial Intelligence Preprint at: http://arxiv.org/abs/1402.4304 (2014). Introduces the Automatic Statistician, translating learned probabilistic models into reports about data.
- Grosse, R. B., Salakhutdinov, R. & Tenenbaum, J. B. Exploiting compositionality to explore a large space of model structures. In Proc. Conference on Uncertainty in Artificial Intelligence 306–315 (2012).
- Schmidt, M. & Lipson, H. Distilling free-form natural laws from experimental data. Science 324, 81–85 (2009).
- Wolstenholme, D. E., O’Brien, C. M. & Nelder, J. A. GLIMPSE: a knowledge-based front end for statistical analysis. Knowl. Base. Syst. 1, 173–178 (1988).
- Hand, D. J. Patterns in statistical strategy. In Artificial Intelligence and Statistics (ed Gale, W. A.) (Addison-Wesley Longman, 1986).
- King, R. D. et al. Functional genomic hypothesis generation and experimentation by a robot scientist. Nature 427, 247–252 (2004).
- Welling, M. et al. Bayesian inference with big data: a snapshot from a workshop. ISBA Bulletin 21, https://bayesian.org/sites/default/files/fm/bulletins/1412. pdf (2014).
- Bakker, B. & Heskes, T. Task clustering and gating for Bayesian multitask learning. J. Mach. Learn. Res. 4, 83–99 (2003).
- Houlsby, N., Hernández-Lobato, J. M., Huszár, F. & Ghahramani, Z. Collaborative Gaussian processes for preference learning. In Proc. Advances in Neural Information Processing Systems 26 2096–2104 (2012).
- Russell, S. J. & Wefald, E. Do the Right Thing: Studies in Limited Rationality (MIT Press, 1991).
- Jordan, M. I. On statistics, computation and scalability. Bernoulli 19, 1378–1390 (2013).
- Hoffman, M., Blei, D., Paisley, J. & Wang, C. Stochastic variational inference. J. Mach. Learn. Res. 14, 1303–1347 (2013).
- Hensman, J., Fusi, N. & Lawrence, N. D. Gaussian processes for big data. In Proc. Conference on Uncertainty in Artificial Intelligence 244 (UAI, 2013).
- Korattikara, A., Chen, Y. & Welling, M. Austerity in MCMC land: cutting the Metropolis-Hastings budget. In Proc. 31th International Conference on Machine Learning 181–189 (2014).
- Paige, B., Wood, F., Doucet, A. & Teh, Y. W. Asynchronous anytime sequential Monte Carlo. In Proc. Advances in Neural Information Processing Systems 27 3410–3418 (2014).
- Jefferys, W. H. & Berger, J. O. Ockham’s Razor and Bayesian Analysis. Am. Sci. 80, 64–72 (1992).
- Rasmussen, C. E. & Ghahramani, Z. Occam’s Razor. In Neural Information Processing Systems 13 (eds Leen, T. K., Dietterich, T. G., & Tresp, V.) 294–300 (2001).
- Rabiner, L. R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 77, 257–286 (1989).
- Gelman, A. et al. Bayesian Data Analysis 3rd edn (Chapman & Hall/CRC, 2013). 100.Lloyd, J. R. & Ghahramani, Z. Statistical model criticism using kernel two sample tests (2015).
版权归原作者 MUKAMO 所有, 如有侵权,请联系我们删除。