图解剖析，递归思想，使用二叉链建立一个二叉树并实现相关操作（数据结构）

在建立一个简单的二叉树之前，我们需要了解二叉树的特点与性质。

二叉树的特点：

    1.二叉树不存在度大于2的结点。

    2.二叉树是有序树，二叉树的子树有左右之分，次序不能颠倒。

    3.空树也是二叉树，二叉树由一个根节点和两颗分别叫做左子树和右子树的二叉树构成。

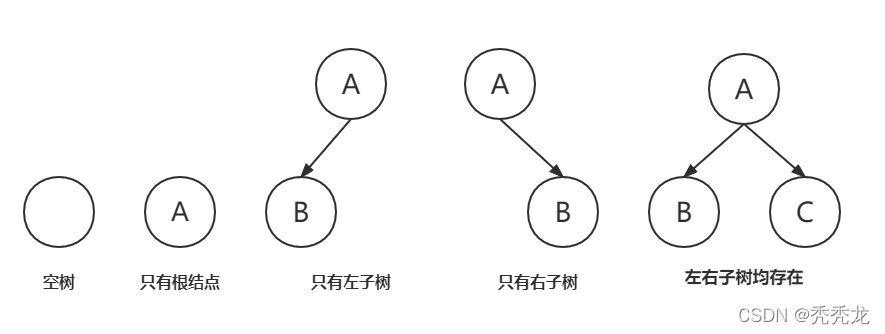
对于任意二叉树，都是由以上几种情况复合而成。

** 二叉树的储存结构：**

** 1.顺序结构**，一般比较适合完全二叉树。

** 2.链式结构**，用一个链表来表示一颗二叉树，用链来表示结点之间的逻辑关系。

    我们则选择使用较为通用的链式结构，链式结构分为二叉链和三叉链，我们选择使用较为简单的二叉链。

用二叉链表示一个二叉树：

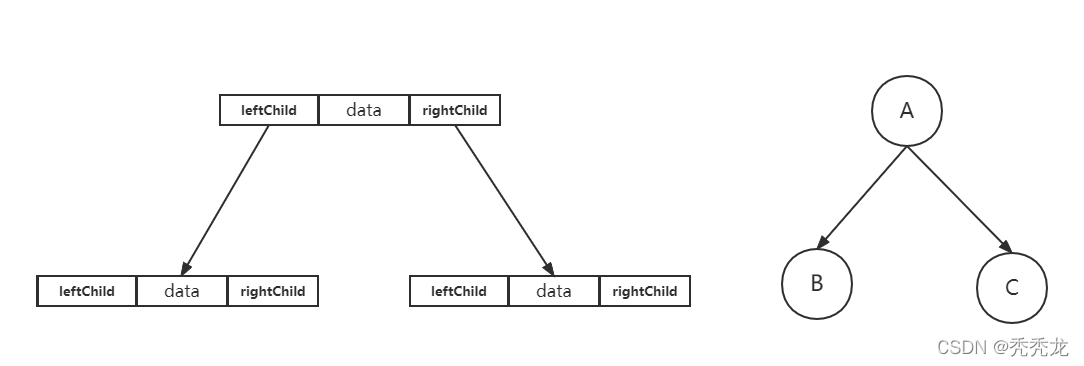
typedef int BTDataType;
typedef struct BTNode {
    struct BTNode* left;//左孩子
    struct BTNode* right;//右孩子
    BTDataType data;//结点的值
}BTNode;

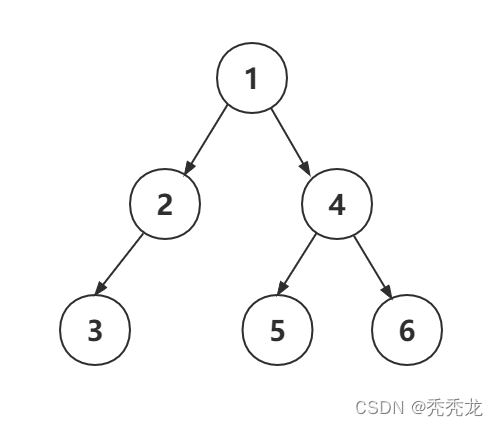
     在初期，我们可以快速创建一个如图的简单二叉树，待完全掌握其结构时，再研究二叉树的真正创建方式。

BTNode* buyBtNode(BTDataType x)
{
    BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
    if (newNode==NULL)
    {
        assert(0);
        return NULL;
    }
    newNode->data = x;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}
BTNode* CreatBinaryTree()
{
 BTNode* node1 = buyNode(1);
 BTNode* node2 = buyNode(2);
 BTNode* node3 = buyNode(3);
 BTNode* node4 = buyNode(4);
 BTNode* node5 = buyNode(5);
 BTNode* node6 = buyNode(6);
 node1->left = node2;
 node1->right = node4;
 node2->left = node3;
 node4->left = node5;
 node4->right = node6;
 return node1;
}

    这样我们就创建了一个简单的二叉树，此后我们会在此二叉树的基础上完成一系列基本操作。

一、二叉树的遍历

    二叉树的遍历时按照某种和规则，依次对二叉树中的结点进行处理，且每个结点只处理一次。

    二叉树的遍历规则有：**前序遍历**，**中序遍历**和**后序遍历**。

    前序遍历：访问根结点的操作发生在遍历其左右子树之前。（根>左>右）

    中序遍历：访问根结点的操作发生在遍历其左右子树之中。（左>根>右）

    后序遍历：访问根结点的操作发生在遍历其左右子树之后。（左>右>根）

void PreOrder(BTNode* root);//前序遍历
void InOrder(BTNode* root);//中序遍历
void PostOrder(BTNode* root);//后序遍历

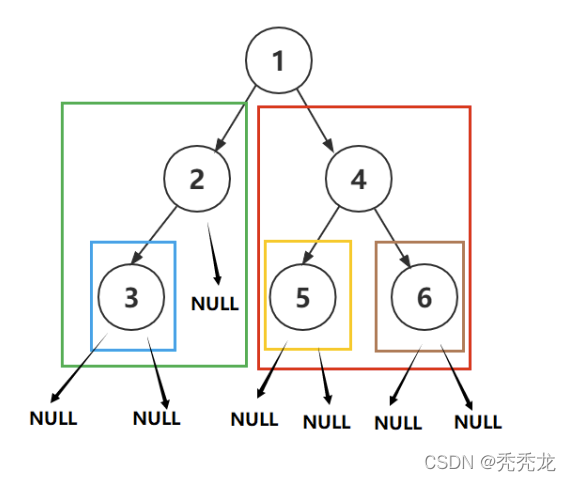
     我们可以把问题分解成：遍历根节点以及根节点的两个子树，即可以用递归的思想解决。

首先解决前序遍历：

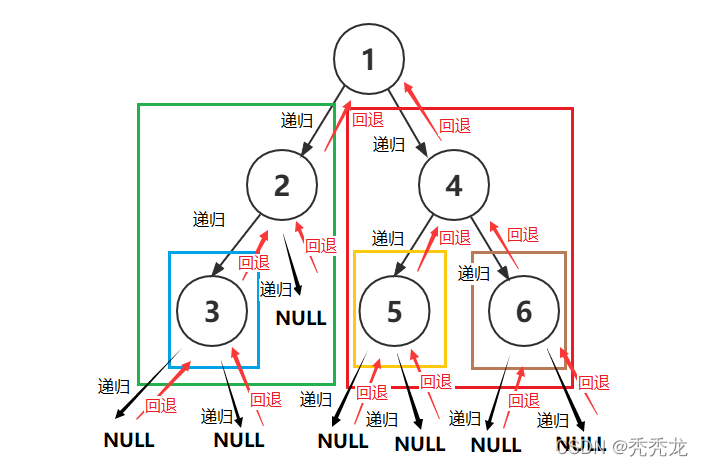
void PreOrder(BTNode* root)
{
    if (root)
    {
        printf("%d ", root->data);
        PreOrder(root->left);
        PreOrder(root->right);
    }
}

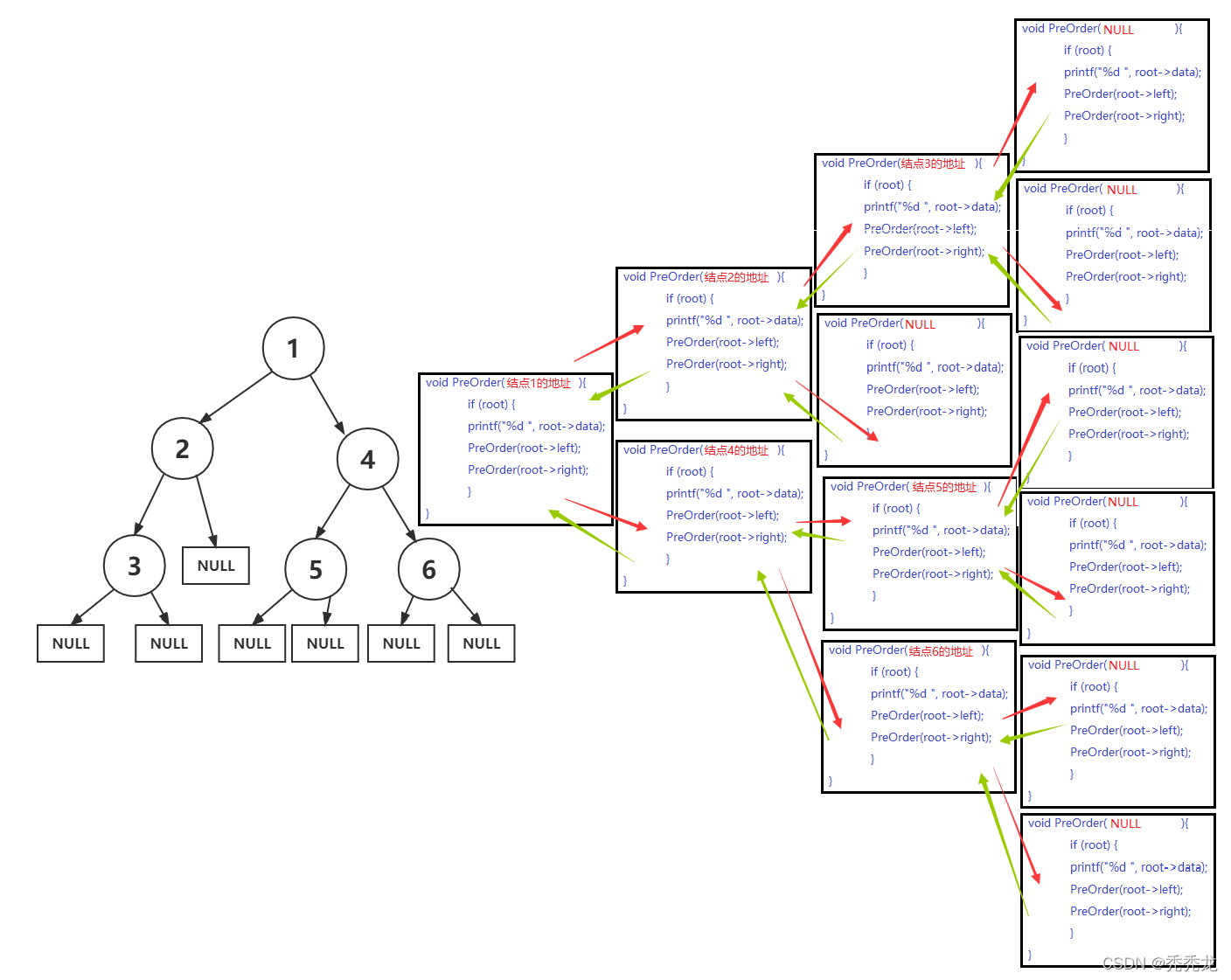
    中序序遍历我们只需先遍历左子树，再遍历根结点，最后遍历右子树；

    同理，后序遍历则是先遍历左子树和右子树，最后遍历根结点。

void InOrder(BTNode* root) //中序遍历
{
    if (root)
    {
        InOrder(root->left); 
        printf("%d ", root->data);
        InOrder(root->right)；
    }
}
void PostOrder(BTNode* root) //后序遍历
{
    if (root)
    {
        PostOrder(root->left);
        PostOrder(root->right);
        printf("%d ", root->data);
    }
}

二、二叉树结点个数以及高度等

int BinaryTreeSize(BTNode* root);// 二叉树节点个数
int BinaryTreeLeafSize(BTNode* root);// 二叉树叶子节点个数
int BinaryTreeHeight(BTNode* root);//求二叉树高度
int BinaryTreeLevelKSize(BTNode* root, int k);// 二叉树第k层节点个数
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);// 二叉树查找值为x的节点

    经过前面对遍历算法的实现，我们发现，二叉树的问题可以使用递归思想解决。

1.二叉树结点个数：

    二叉树的结点个数就等于根结点个数（1）加上其左右子树的节点个数。

int BinaryTreeSize(BTNode* root)
{
    if (NULL==root)
    {
        return 0;
    }
    return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

2.二叉树的叶子结点个数

    自身下面不再链接有结点的结点叫做叶子结点，即度为0的结点；同样我们可以把问题分解成

：二叉树的叶子结点数就等于二叉树的左右子树的叶子结点数之和。

int BinaryTreeLeafSize(BTNode* root) {
    if (NULL==root)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

3.求二叉树的高度；

    相同的递归思想：二叉树的高度等于其左右子树中更高的子树的高度加1。

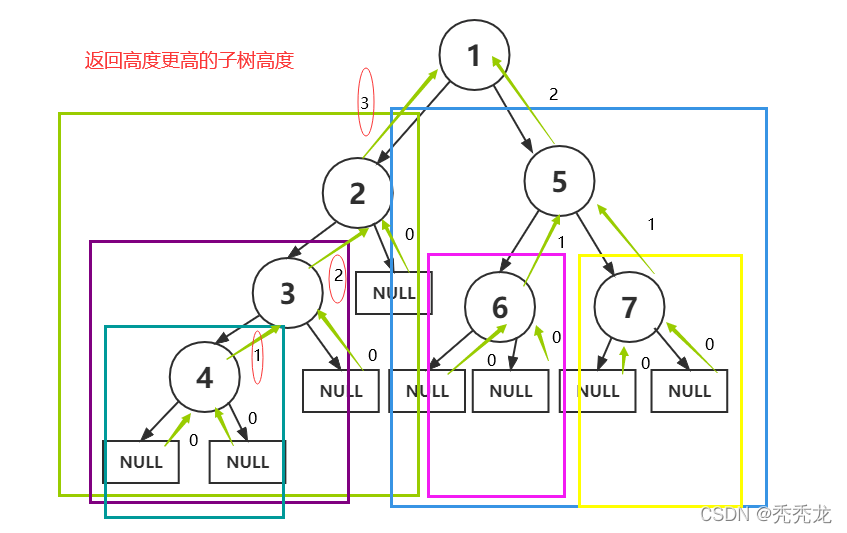
int BinaryTreeHeight(BTNode* root)
{
    if (root==NULL)
    {
        return 0;
    }
    int leftheight = BinaryTreeHeight(root->left);
    int rightheight = BinaryTreeHeight(root->right);
    return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

4.二叉树第k层结点的个数

    首先，**k不能小于等于0**，其次，我们可以将问题分解为**求二叉树子树的第k-1层的结点个数。**

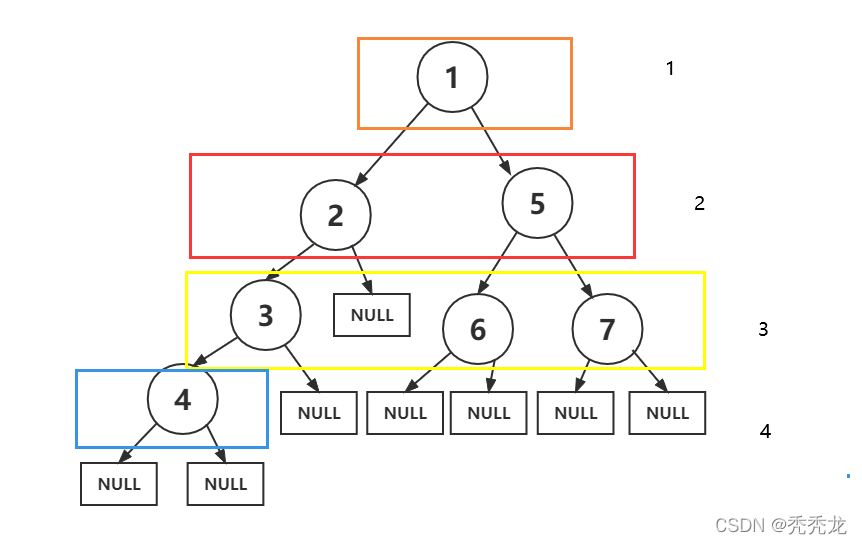
当k==1时，相当于求子树的根节点有几个，直接返回1；

int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if (k<=0||NULL==root)
    {
        return 0;
    }
    if (k==1)
    {
        return 1;
    }
    return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
    
}

5.寻找二叉树内值为x的结点。

    依旧是递归思想，寻找二叉树内值为x的结点也就是看根节点是否是值为x的结点和查找子树中有无值为x的结点；

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    BTNode* ret = NULL;
    if (NULL == root)
    {
        return NULL;
    }
    if(root->data==x)
    {
        return root;
    }
    //ret= BinaryTreeFind(root->left,x);
    if (ret = BinaryTreeFind(root->left, x))
    {
        return ret;
    }
    return BinaryTreeFind(root->right, x);
}

    先找根结点是否值为x，再找左子树中有无值为x的结点，如果没有返回NULL；最后找右子树中有无值为x的结点。

三、二叉树的创建和销毁

    经过前面对二叉树的各项操作，相信大家已经较为充分的理解了二叉树的结构。下面我们来看看究竟如何创建一个二叉树。

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi, int size);
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* buyBtNode(BTDataType);//创建一个结点
void BinaryTreeDestory(BTNode** root);// 二叉树销毁

1.创建二叉树。

    我们可以尝试按照前序遍历的顺序创建一个二叉树；首先可以让用户提供一个数组。

int a[]={1,2,3,4,5,6};

    我们按前序遍历尝试创建二叉树，先写一个创建新结点的函数；

BTNode* buyBtNode(BTDataType x)//创建一个结点
{
    BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
    if (newNode==NULL)
    {
        assert(0);
        return NULL;
    }
    newNode->data = x;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

    创建一个二叉树就相当于**创建一个根节点，再创建他的左右子树**；

BTNode* BinaryTreeCreate(BTDataType* a,int* pi,int size)
{
    if (size>*pi)
    {
    BTNode* newNode = buyBtNode(a[*pi]);
    (*pi)++;
    newNode->left = BinaryTreeCreate(a,pi,size);
    (*pi)++;
    newNode->right = BinaryTreeCreate(a,pi,size);
    return newNode;
    }
    return NULL;
}

此时我们发现，他会一直创建左子树，如图：

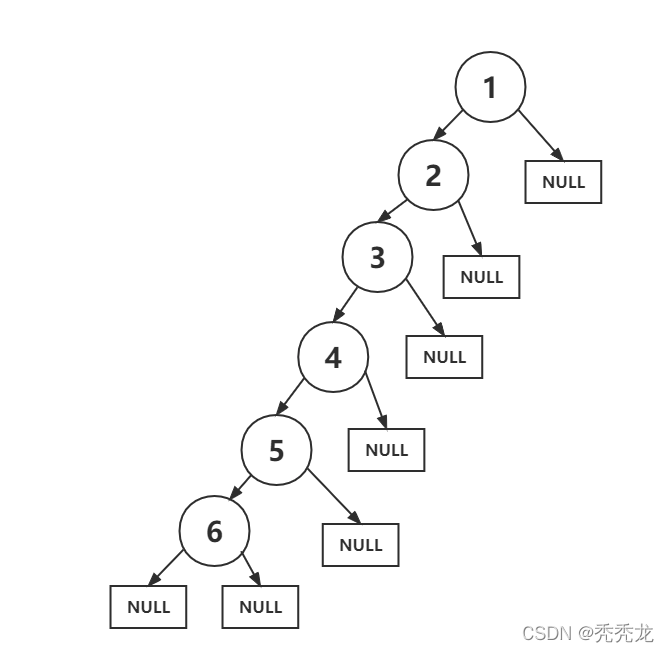
经过调试发现，我们的程序无法分辨叶子结点；此时我们可以使用一个特殊的值来表示NULL

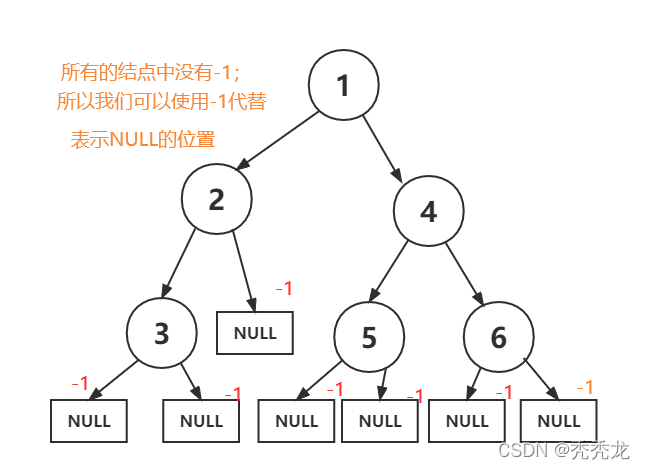
     此时用户需要给程序的序列是：

int a[] = { 1,2,3,-1,-1,-1,4,5,-1,-1,6 };

    此时需要给函数多传一个参数，来告诉程序用户用哪个值代替NULL的位置；当a[*pi]==n时，返回NULL；

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi,int size)
{
    if (size>*pi&&a[*pi]!=n)
    {
    BTNode* newNode = buyBtNode(a[*pi]);
    (*pi)++;
    newNode->left = BinaryTreeCreate(a, n, pi,size);
    (*pi)++;
    newNode->right = BinaryTreeCreate(a, n, pi,size);
    return newNode;
    }
    return NULL;
}

    这样我们就成功创建了一个二叉树。

2.二叉树的销毁

    我们的二叉树是使用malloc函数创建再堆上的，如果不手动释放，就会造成内存泄漏。二叉树的销毁与创建有一点不同，由于我们的二叉树是使用二叉链表创建，结点与结点之间由指针连接，如果先free根结点，我们就找不到子结点了，所以我们释放内存时，应该**先释放左右子树的空间，再释放根节点的空间**。

void BinaryTreeDestory(BTNode** root)
{
    if (NULL==*root)
    {
        return;
    }
    BinaryTreeDestory(&((*root)->left));
    BinaryTreeDestory(&((*root)->right));
    free(*root);
    *root = NULL;
}

     传二级指针的原因：我们创建二叉树时，创建了一个指针变量指向这个在堆上的二叉树，当释放完空间时，这个指针就变成野指针了。

测试程序：

int main()
{
    int a[] = { 1,2,3,-1,-1,-1,4,5,-1,-1,6 };
    int pi = 0;
    BTNode* Node=BinaryTreeCreate(a,-1,&pi,sizeof(a)/sizeof(a[0]));
    PreOrder(Node);//123456
    printf("\n");
    InOrder(Node);//321546
    printf("\n");
    PostOrder(Node);//325641
    printf("\n");
    printf("%d \n",BinaryTreeSize(Node));//6
    printf("%d \n", BinaryTreeLeafSize(Node));//3
    printf("%d \n", BinaryTreeLevelKSize(Node,2));//2
    printf("%d\n",BinaryTreeFind(Node,6)->data);//6
    BinaryTreeDestory(&Node);
    return 0;
}