三天三夜整理最难数据结构(红黑树)之理论篇
前言
同学们都非常好奇校园的门禁系统、车站中的身份证识别系统和我们经常使用的查单词,背单词(百词斩,百度翻译)的软件是怎么设计出来的,其底层就是红黑树的K_Val模型,现在机会来了,阅读完本文,你将达到设计诸如此类系统的入门要求
其实,如果有学过数据结构的小伙伴肯定会说,顺序表和链表也可以用来存储数据然后来做这个呀,其实不然,如果采用顺序表或者链表来做这个的话,那么效率就会特别低,举个例子:如果用顺序表或者链表来做这个的话,那么如果需要存储1亿个单词及其中文意思,那么我们在查找的时候,系统就需要去内存中查找1亿次,才能得出结果,但是利用红黑树来做的话,只需要查找几十次就可以得出结果了,其所需要的时候是非常短的,因此,学习红黑树就显得非常重要了。
二话不说,先上一棵红黑树示意图!!!
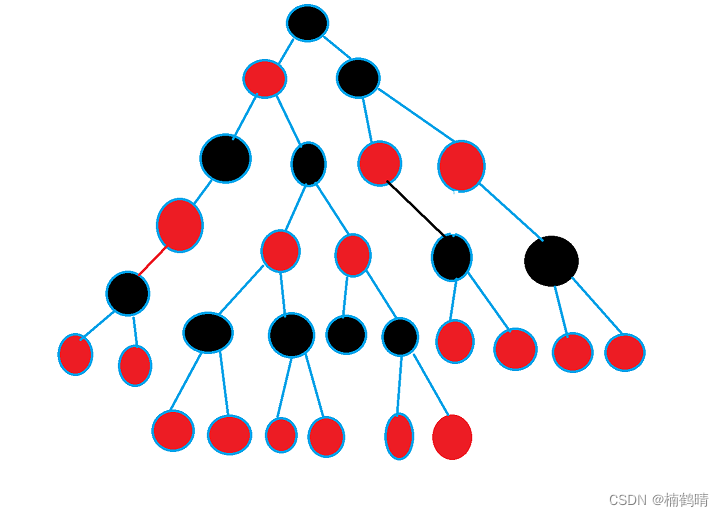
本节主要内容
红黑树的性质
红黑树中数据的插入(分类讨论)
总结
红黑树的性质
1. 树中的结点的颜色不是红色就是黑色
2. 树的根节点一定是黑色
3. 红色结点的两个孩子一定是黑色的(红黑树中不能出现连续的红色结点)
4. 树中的任意结点到叶子结点的所有简单路径的黑色结点的数量都是一样的
5. 树中的叶子结点(空结点)的颜色是黑色的
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
答:由红黑树的性质,我们不难得出:
树中的最长路径就是红色结点比较多的路径,又由于红色结点的两个孩子的颜色一定是黑色的(不能出现连续的红色结点),因此最极端的红黑树中最长的路径的情况就应该是红色与黑色的结点交替出现的情况
最极端的红黑树中的最短路径就应该是黑色结点比较多的路径,那么最极端的情况就是最短路径中的结点都是黑色的
我们这里处理最极端的最长路径与最短路径的情况:
最短路径的情况:路径中只有黑色的结点,数量记为x,因为红黑树的性质,从一个结点出发到叶子结点的所有简单路径的黑色结点的数量是一样的,因此,在最长的路径中所包含的黑色结点的数量和最短路径的黑色结点的数量是相同的,即为x,那么由于最长路径的情况就是红色结点和黑色结点是交替出现的,因此,最长路径中红色结点的数量和黑色结点的数量是相同的,也为x。
因此,
最短路径中结点的数量 = 黑色结点的数量+红色结点的数量 = x + 0 = x
最长路径中结点的数量 = 黑色结点的数量+红色结点的数量 = x + x = 2x
故
最长路径中结点的数量 / 最短路径中结点的数量 = 2x / x = 2
其他情况就是,最长路径中的黑色结点的数量会增加,最短路径中红色结点的数量会增加,其比值小于2
红黑树的插入:首先按照搜索树的插入对红黑树进行插入数据。插入数据之后,再根据红黑树的性质分情况对树进行调整
思考:插入的新结点是黑色结点还是红色结点?
答:红色结点
如果插入黑色结点,那么由性质4:红黑树中的任意结点到叶子结点中的所有简单路径的黑色结点的数量是一样的,因此,如果在某一路径插入黑色,那么势必会影响到该结点其他路径的黑色结点的数量,那么情况就会比较复杂,难以处理。
如果插入红色结点,那么由于性质3:红色结点的孩子结点一定是黑色的(不能出现连续的红色结点),因此,可能会出现连续的红色结点而导致不符合红黑树的性质(当插入的新节点的父亲是红色结点时就会破坏红黑树的性质),这种情况只是影响当前结点和父亲结点,处理比较简单。
综上,新增的结点为红色比较适宜
插入之后,如果父亲结点是黑色的,就不需要进行调整,如果插入的结点的父亲结点是红色的,那么这就违反红黑树的第三条规则,即不能出现连续的红色结点
在调整之前一定要先记录树中的几个关键的结点:
grandfather
,
parent
,
uncle
,
cur
cur:新插入的结点parent:新插入结点的父亲结点uncle:新插入结点的叔叔结点grandfather:新插入结点的父亲的父亲,即新插入结点的爷爷基本模型
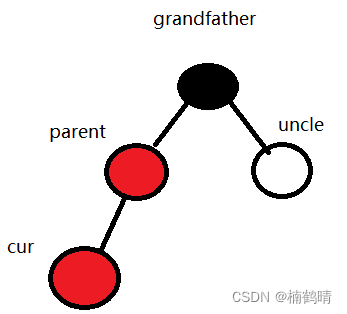
其中,有三个结点的颜色是固定的,分别为
grandfather
,
parent
,
cur
cur:由前面的分析易知,插入的新节点为红色比较合适parent:由于红黑树中不能出现连续的红色结点,如果parent为黑色的话是不需要进行调整的,因此,我们考虑的是parent为红色的情况grandfather:parent为红色,由红黑树的性质三也可以知道,grandfather必定为黑色,如果为红色,那么该树就违反了红黑树的第三条性质。 主要会发生变化的就是**uncle的颜色,uncle的颜色有三种情况,不存在,红色,黑色**
下面将根据
uncle
结点可能出现的情况进行分类讨论:
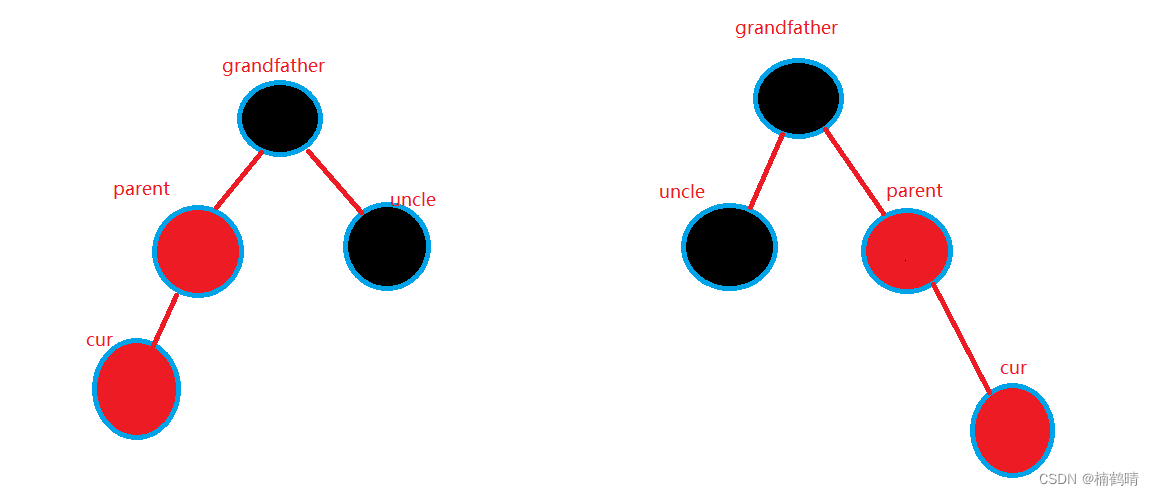
- 情况一:
parent为红色,**uncle为红色(只需要调色,不需要旋转**) - 如图
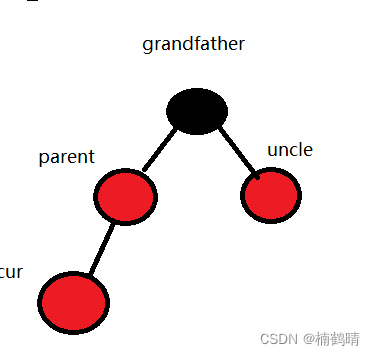
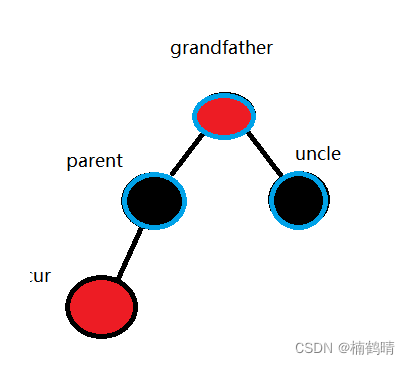
处理方法:**将
parent
,
uncle
变为黑色,将
grandfather
变成红色**。
parent,uncle变为黑色:解决了出现连续红色结点的问题,同时保证了性质4(从任意结点(这里指grandfather结点)出发到叶子结点的所有路径的黑色结点的数量是相同的)- 将
grandfather变成红色:处理的树可能是红黑树中的子树,就要保证子树中所有路径的黑色结点与处理前相同(处理前各路径黑色结点的数量为1,处理后各路径黑色结点的数量也为1),这样才不会影响到树的另外的子树(即不会违法红黑树的第三条性质)
温馨提示:上述情况是
parent
是
grandfather
的左孩子,根据对称原则,
parent
也有可能是
grandfather
的右孩子,因此,
cur
可以插入在
parent
的左或者右,一共会有四种子情况,而这四种子情况是对称的,其操作方法是一模一样的
- 情况二:
parent为红色,**uncle不存在(单旋+调色**) - 处理过程如图
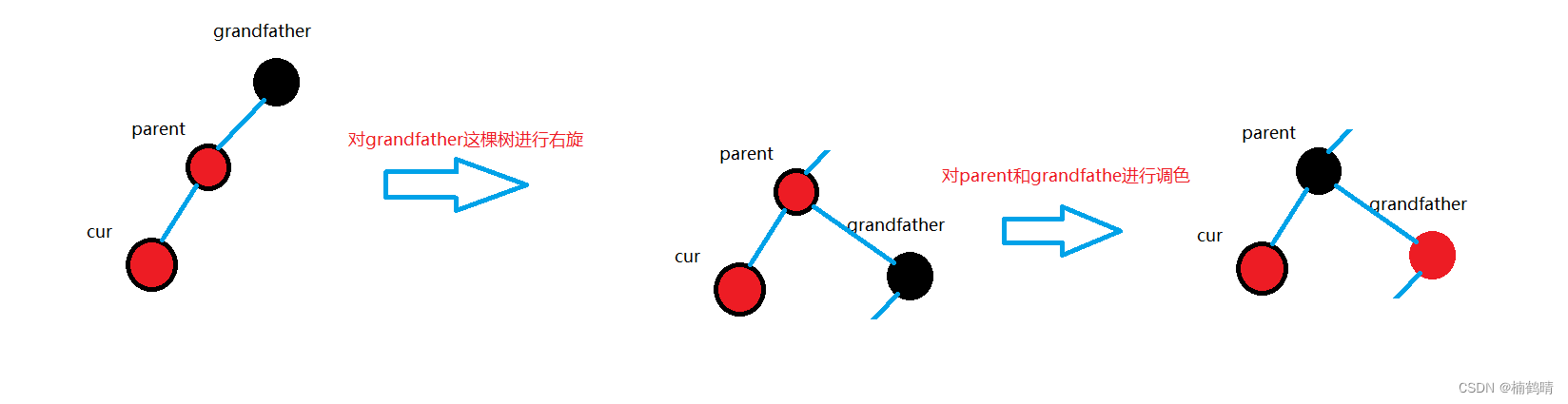 这里采用了两步操作:右旋和调色 右旋:在AVL树章节中将重点讲解,因为左树中的高度比较大,因此对左树进行右旋一下才能使整棵树保持相对平衡 调色:右旋之后,将
这里采用了两步操作:右旋和调色 右旋:在AVL树章节中将重点讲解,因为左树中的高度比较大,因此对左树进行右旋一下才能使整棵树保持相对平衡 调色:右旋之后,将grandfather结点调成红色和将parent结点调成黑色,因为进行右旋之后,parent到这棵子树的根去了,grandfather到下面去了,为了保证这棵子树的中所有路径的黑色结点的数量保持不变,需要这样进行调色
温馨提示:上述情况是上述情况是
parent
是
grandfather
的左孩子,由对称原则,
parent
也有可能是
grandfather
的右孩子,
parent
是
grandfather
的左孩子时,
cur
是
parent
的左孩子,
parent
是
grandfather
的右孩子时,
cur
是
parent
的右孩子,都是属于这种情况,一共有两种情况,完全对称,处理方法一模一样
- 情况三:
parent为红色,**uncle存在且为黑色(单旋+调色**) - 这种情况一定是由情况一变过来的
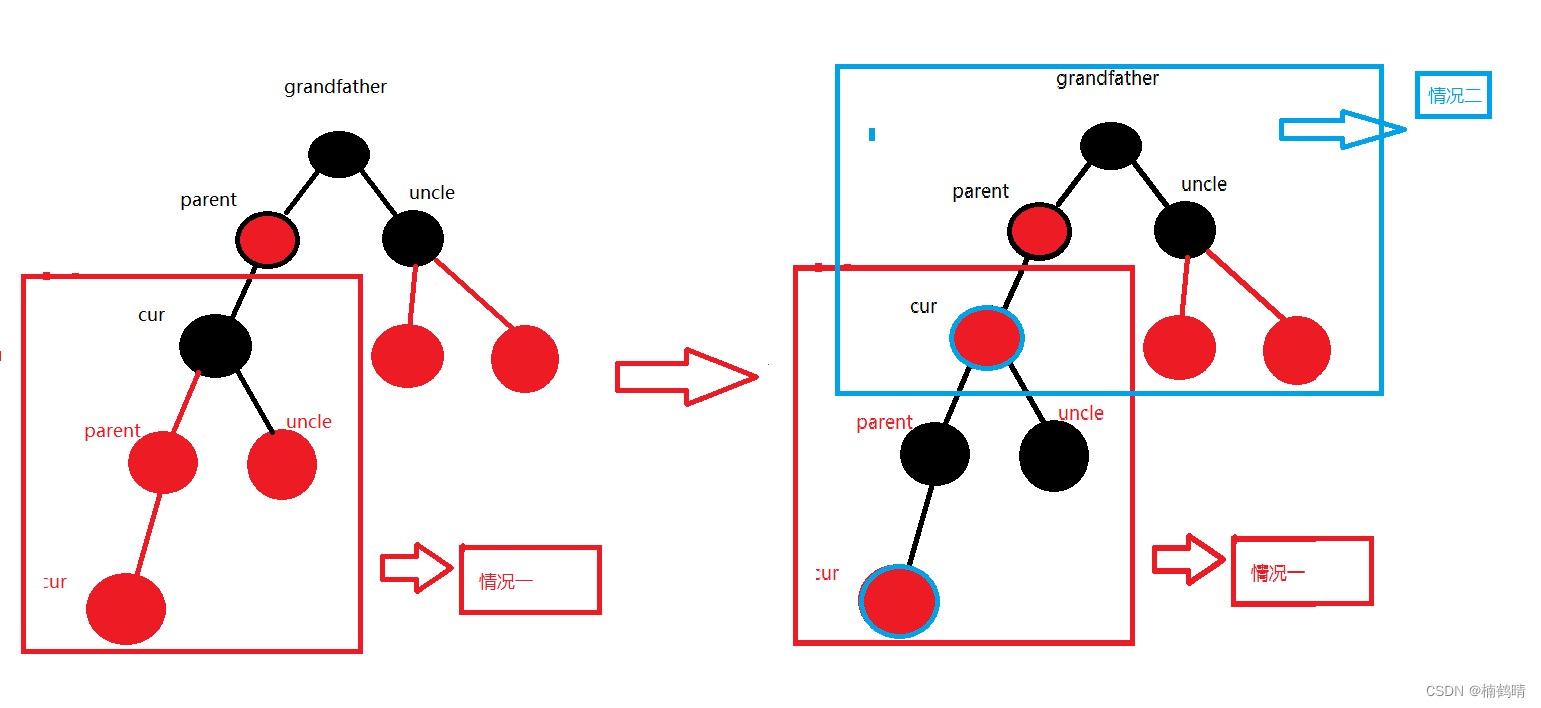
- 处理方法:
- 对整棵树进行右旋
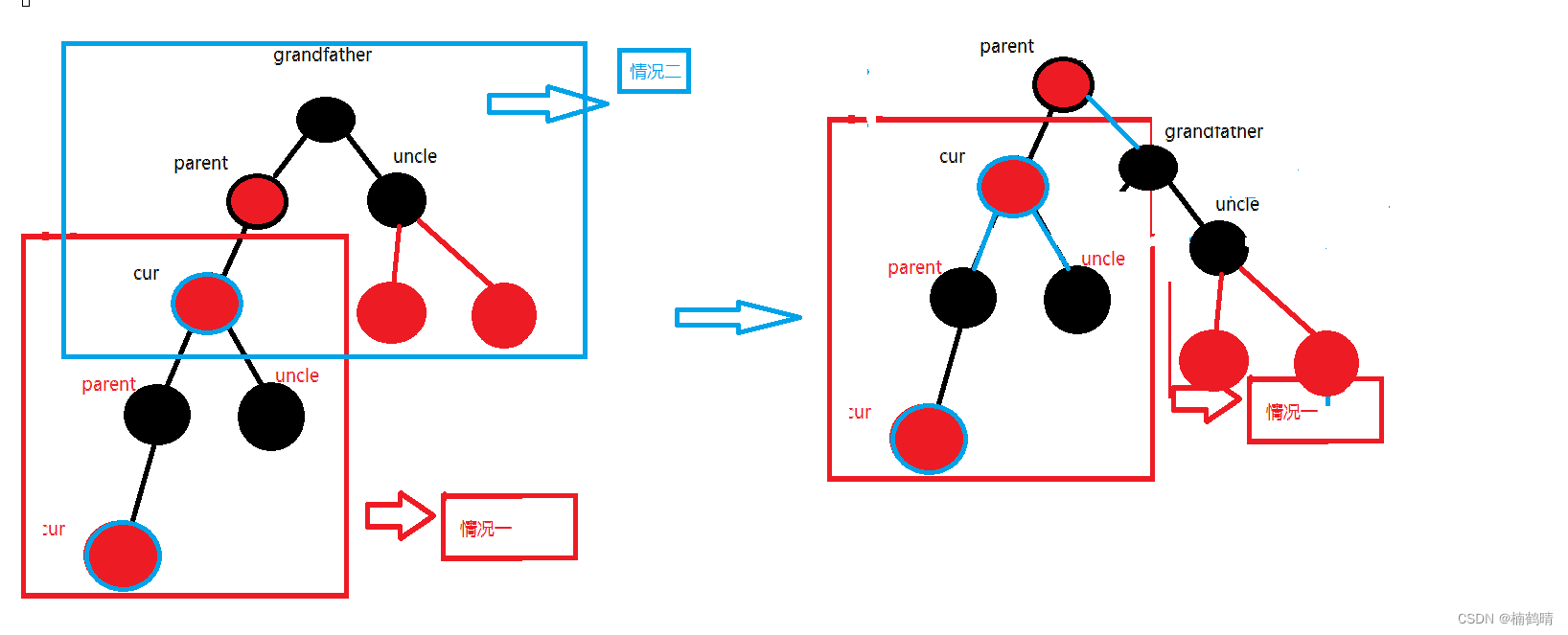 对
对parent和grandfather进行调色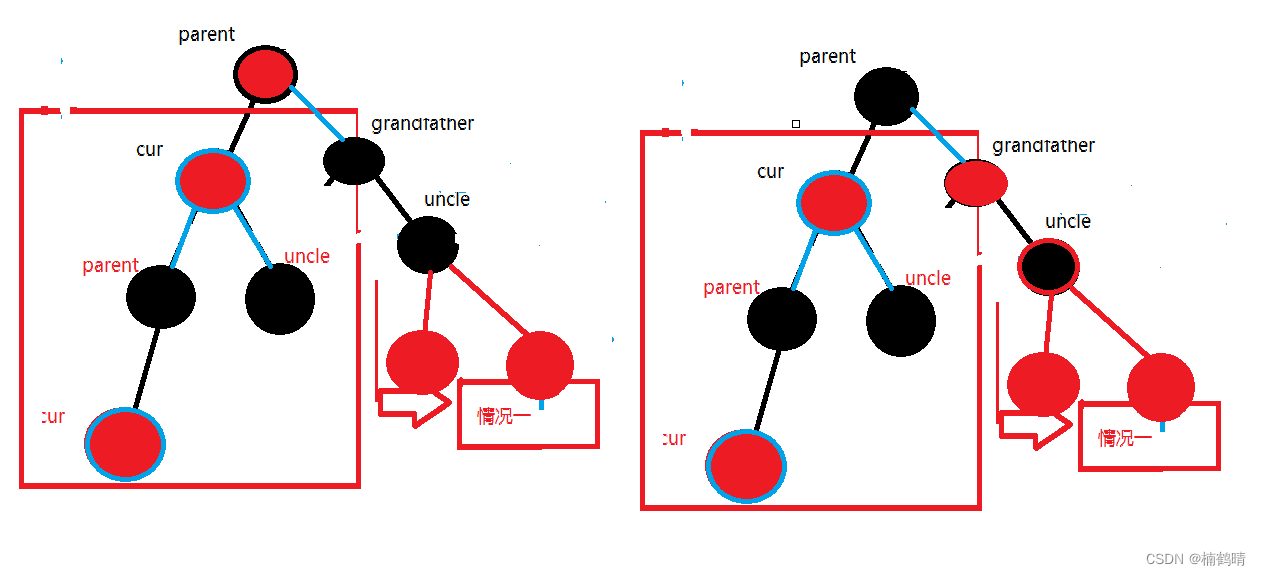 跟前面的一种情况是一样的,将
跟前面的一种情况是一样的,将parent改为黑色,将grandfather改为红色
温馨提示:上述情况是上述情况是
parent
是
grandfather
的左孩子,由对称原则,
parent
也有可能是
grandfather
的右孩子,
parent
是
grandfather
的左孩子时,
cur
是
parent
的左孩子,
parent
是
grandfather
的右孩子时,
cur
是
parent
的右孩子,都是属于这种情况,一共有两种情况,完全对称,处理方法一模一样
情况四:
parent
为红色,**
uncle
不存在(双旋+调色),这里与情况二和情况三的区别在于,新插入的结点的位置不同**
- 如果**
parent是grandfather的左孩子,cur是parent的左孩子**,那么这种情况是第二和第三情况 - 如果
parent是grandfather的左孩子,**cur是parent的右孩子**,那么这种情况是第四种情况 - 情况图:
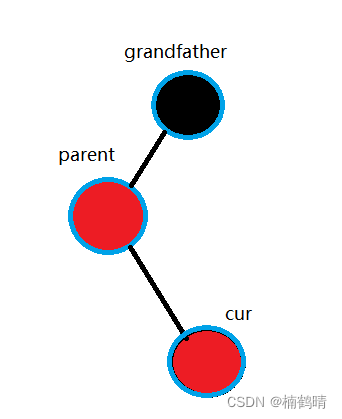
- 处理方法:
- 将
parent所在子树进行左旋(转化成第二、三种情况)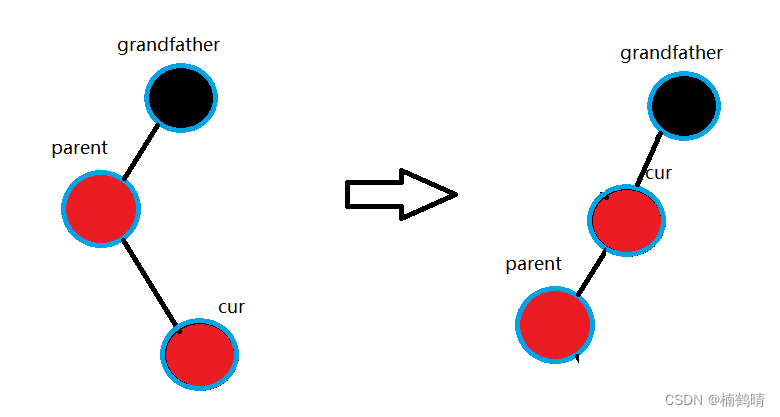
- 将
grandfather所在树进行右旋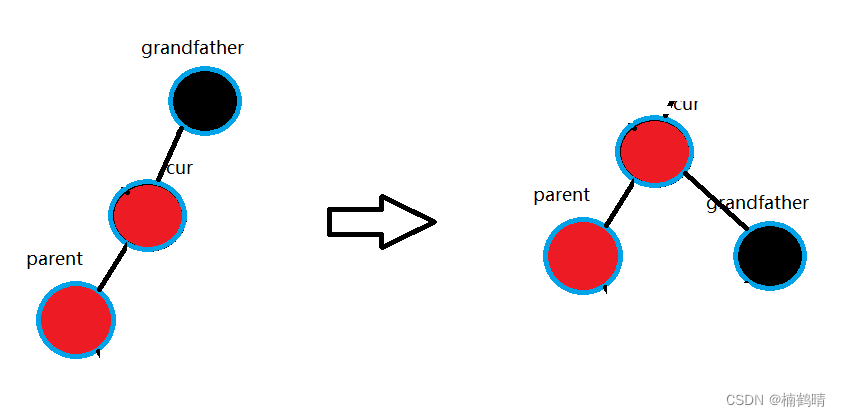
- 调色:将
cur调成黑色,将grandfather调成红色(这里的话,在调色前也可以交换parent和``cur的指针,那么就和第二、三种情况一模一样了)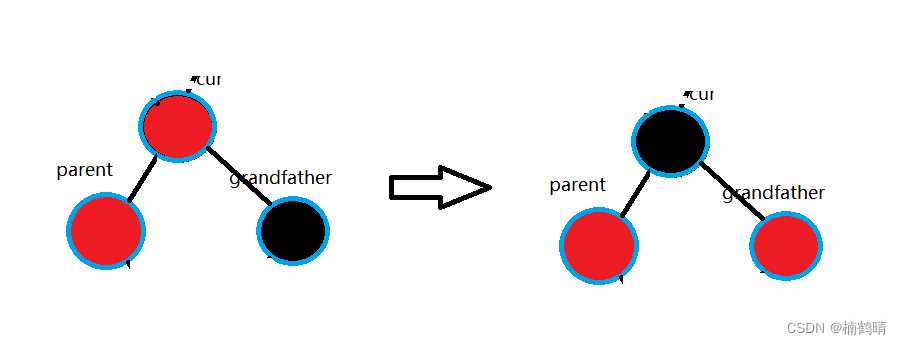
温馨提示:上述情况是上述情况是
parent
是
grandfather
的左孩子,由对称原则,
parent
也有可能是
grandfather
的右孩子,
parent
是
grandfather
的左孩子时,
cur
是
parent
的右孩子,
parent
是
grandfather
的右孩子时,
cur
是
parent
的左孩子,都是属于这种情况,一共有两种情况,完全对称,处理方法一模一样
- 情况五:
parent为红色,**uncle存在且为黑色(双旋+调色)**,这里与情况二和情况三的区别在于,新插入的结点的位置不同 - 一定是由情况一变过来的
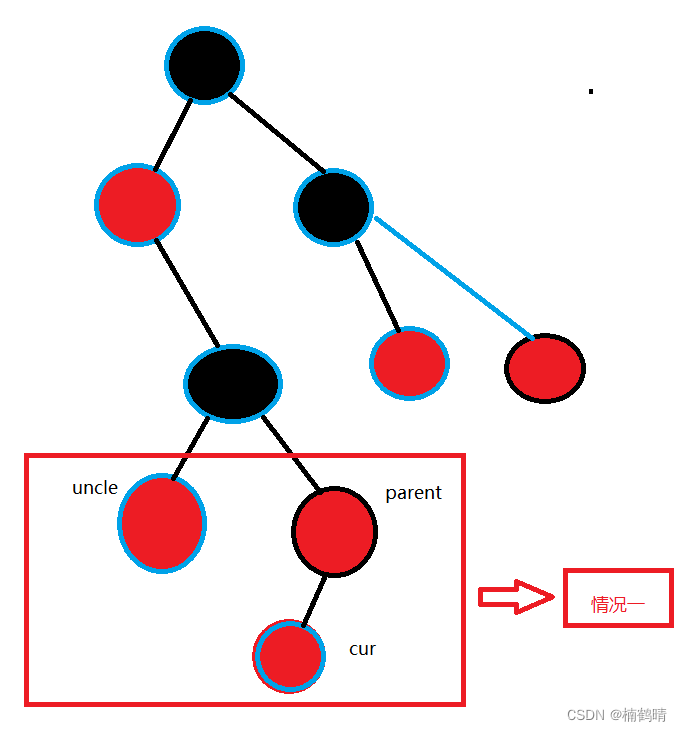
- 由情况一变过来
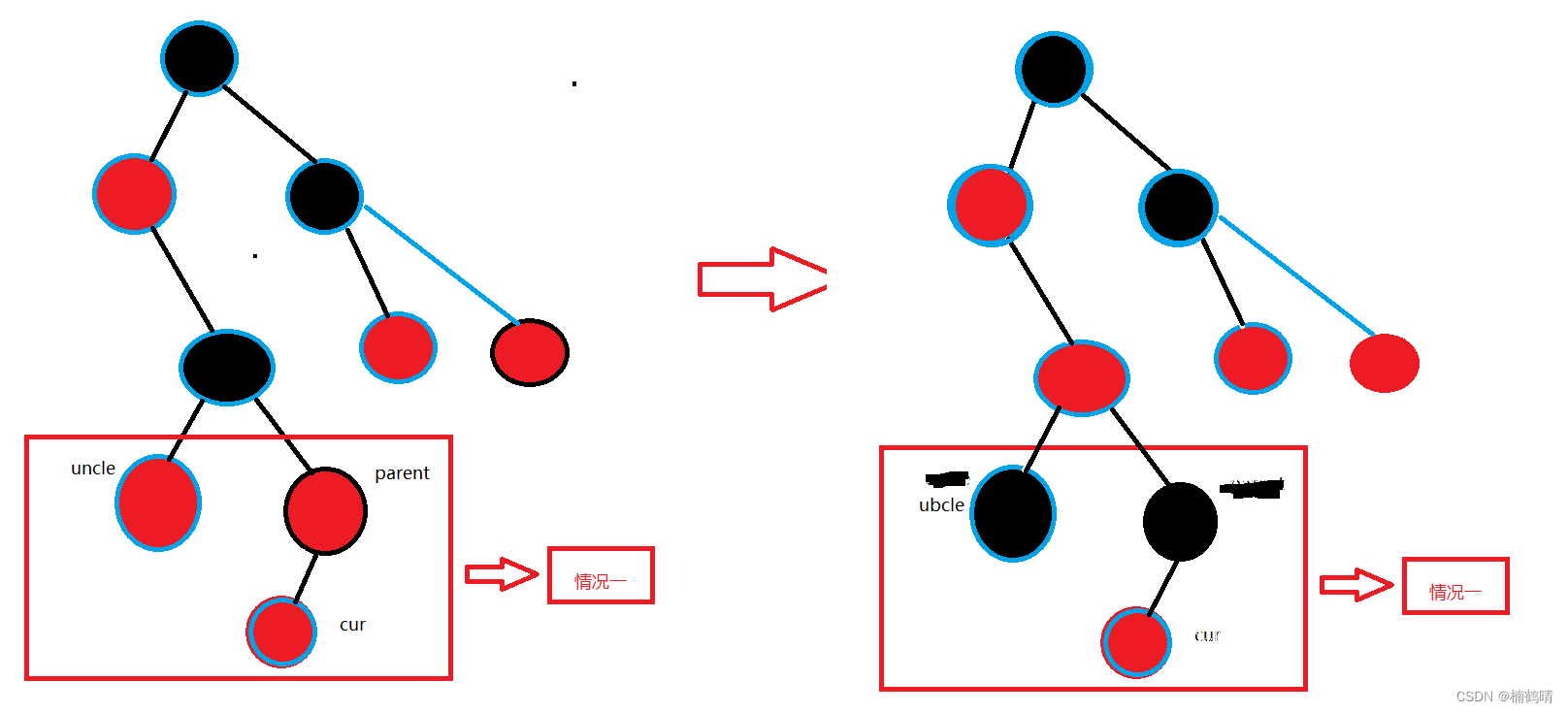
- 对
parent所在树进行左旋,转化成第二,第三种情况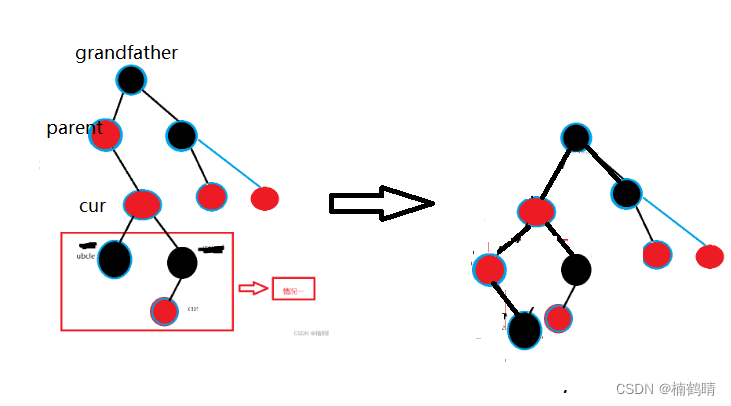
- 对
grandfather所在树进行右旋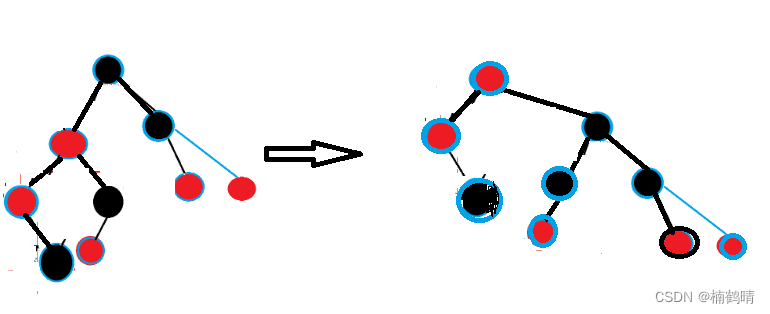
- 调色:和上面的情况一样
温馨提示:上述情况是上述情况是
parent
是
grandfather
的左孩子,由对称原则,
parent
也有可能是
grandfather
的右孩子,
parent
是
grandfather
的左孩子时,
cur
是
parent
的右孩子,
parent
是
grandfather
的右孩子时,
cur
是
parent
的左孩子,都是属于这种情况,一共有两种情况,完全对称,处理方法一模一样
总结
情况一(四种子情况):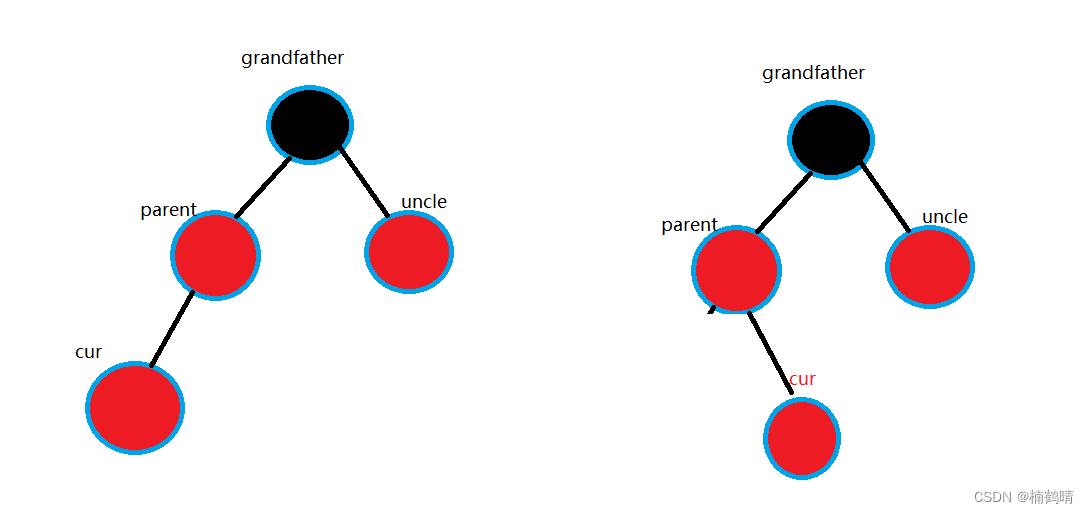
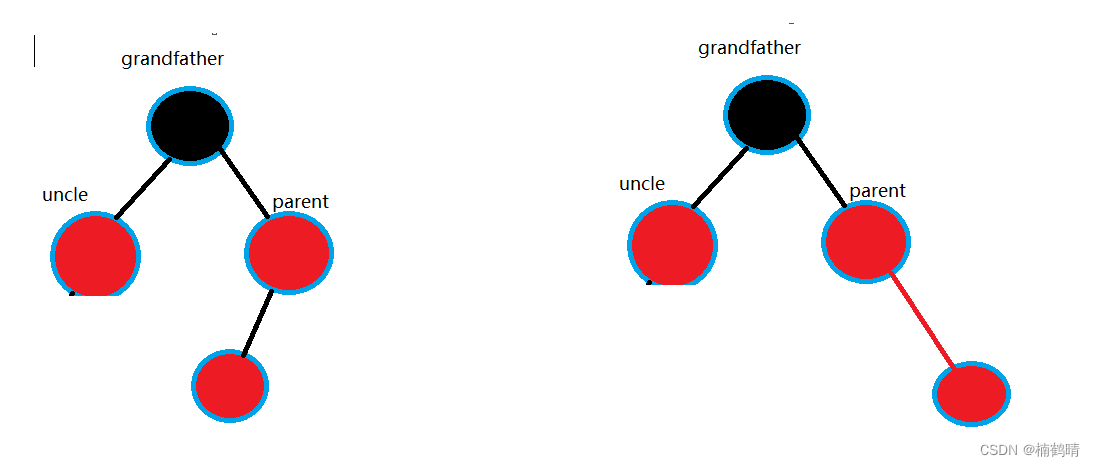
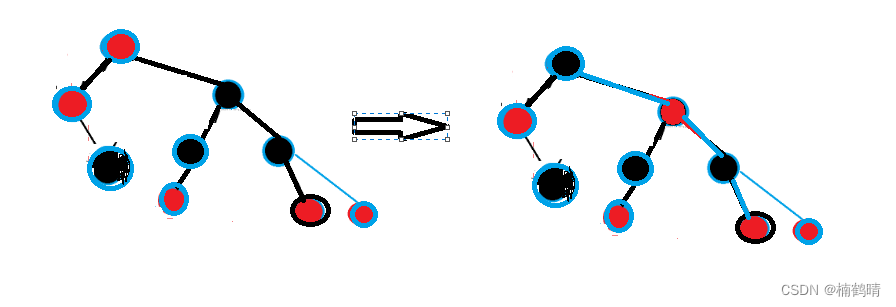
情况二和情况三其实可以合并成一种(下面的图是由情况一变过来的)(四种子情况)

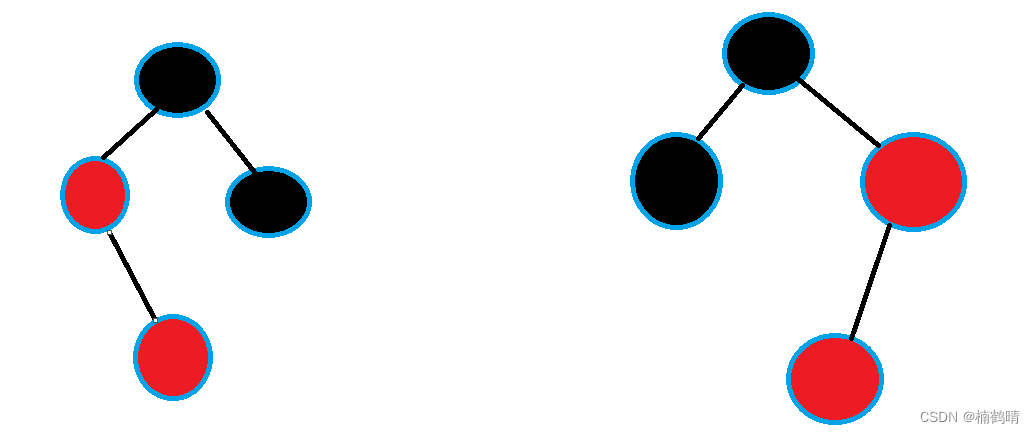
情况四和情况五其实可以合并成一种(下面的图是由情况一变过来的)(四种子情况)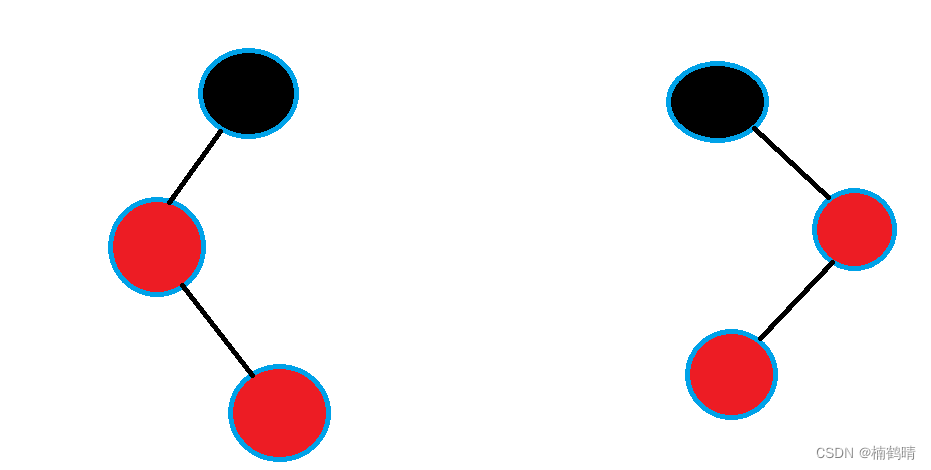
版权归原作者 楠鹤晴 所有, 如有侵权,请联系我们删除。