合肥工业大学人工智能原理课程实验-波士顿房价预测

1.实验内容

    波士顿房地产市场竞争激烈，而你想成为该地区最好的房地产经纪人。为了更好地与同行竞争，你决定运用机器学习的一些基本概念，帮助客户为自己的房产定下最佳售价。幸运的是，你找到了波士顿房价的数据集，里面聚合了波士顿郊区包含多个特征维度的房价数据。你的任务是用可用的工具进行统计分析，并基于分析建立优化模型。这个模型将用来为你的客户评估房产的最佳售价 

◼ 具体要求：

➢ 任务输入：波士顿房子的各类属性数据。

• ➢ 任务输出：设计模型，评估房子的最佳售价。

➢ 数据集地址：链接: https://pan.baidu.com/s/1xF8uwM-9kGqk1GGtufsKuw 提取码: vzws

➢ 方法不限，要求提交整个算法源代码，模型结果，算法分析等内容

2.实验环境

** ** ** 1.硬件**

    RedmiG 2022版 显存16GB  内存512GB cpu：3050

** 2.软件（运行环境）**

    显卡：NVIDIA显卡，CUDA 11.7。

  系统与环境：Windows11操作系统，Anaconda3的base虚拟环境。

    IDE：Pycharm Community集成开发环境

    深度学习框架：PyTorch深度学习框架，基于GPU版本。

3.实验思路（算法分析）

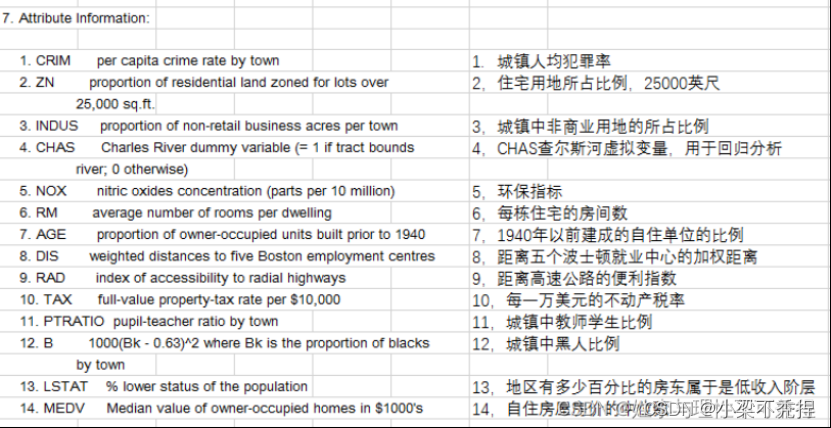
     波士顿房价数据集是20世纪70年代中期波士顿郊区房价的中位数，统计了当时城市的14个指标与房价的数据，试图能找到那些指标与房价的关系。

数据集中各特征的含义如下：

本实验采用线性回归的方法建立模

4.实验过程、步骤

1.导入所需的库：numpy、pandas和matplotlib.pyplot。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

2.定义线性回归类，包含两个方法：fitness和predicted。

** fitness方法用于训练线性回归模型。输入参数为特征矩阵Date_X_input、目标变量Date_Y、学习率learning_rate（默认值为0.5）和正则化系数lamda**（默认值为0.03）。

    在fitness方法中，首先获取样本个数和属性个数。然后对特征矩阵进行扩展，添加一列全为1的常数项。接着初始化待调参数theta为全零向量。设置**最大迭代次数**Max_count为1e8，设置阈值value为1e-8，设置阈值计数count为10。

    def fitness(self, Date_X_input, Date_Y, learning_rate=0.5, lamda=0.03):
        sample_num, property_num = Date_X_input.shape# 获取样本个数、样本的属性个数
        Date_X = np.c_[Date_X_input, np.ones(sample_num)]
        self.theta = np.zeros([property_num + 1, 1])        # 初始化待调参数theta
        Max_count = int(1e8)  # 最多迭代次数
        last_better = 0  # 上一次得到较好学习误差的迭代学习次数
        last_Jerr = int(1e8)  # 上一次得到较好学习误差的误差函数值
        threshold_value = 1e-8  # 定义在得到较好学习误差之后截止学习的阈值
        threshold_count = 10  # 定义在得到较好学习误差之后截止学习之前的学习次数

 **   predicted方法**用于预测新的数据。输入参数为特征矩阵X_input。首先获取样本个数，对特征矩阵进行扩展，添加一列全为1的常数项。然后计算预测值predict，返回预测结果。

    def predicted(self, X_input):
        sample_num = X_input.shape[0]
        X = np.c_[X_input, np.ones(sample_num, )]
        predict = X.dot(self.theta)
        return predict

3.迭代训练模型

    使用for循环进行迭代训练。在每次迭代中，计算预测值predict，计算损失函数J_theta。更新参数theta，根据损失函数的变化值判断是否提前结束迭代。如果满足条件，则更新last_Jerr和last_better。如果连续threshold_count次迭代后仍未满足条件，则跳出循环。每50次迭代打印一次损失函数的值。

  for step in range(0, Max_count):
            predict = Date_X.dot(self.theta)            # 预测值
            J_theta = sum((predict - Date_Y) ** 2) / (2 * sample_num)            # 损失函数
            self.theta -= learning_rate * (lamda * self.theta + (Date_X.T.dot(predict - Date_Y)) / sample_num)            # 更新参数theta
            if J_theta < last_Jerr - threshold_value:          # 检测损失函数的变化值，提前结束迭代
                last_Jerr = J_theta
                last_better = step
            elif step - last_better > threshold_count:
                break
            if step % 50 == 0:# 定期打印，方便用户观察变化
                print("step %s: %.6f" % (step, J_theta))

4.数据可视化

    读取波士顿房价数据集，调用**property_label函数**将数据集中的样本属性进行分割，制作X和Y矩阵。然后调用standardization函数对X进行归一化处理。接着创建线性回归模型对象，调用fitness方法训练模型。最后调用predicted方法预测新的数据，计算预测误差，并绘制实际值和预测值的图像。

if __name__ == "__main__":
    data = pd.read_csv("波士顿房价/housing-data.csv", header=None)
    Date_X, Date_Y = property_label(data)    # 对训练集进行X，Y分离
    Standard_DateX, Maxx, Minx =  standardization (Date_X)    # 对X进行归一化处理，方便后续操作
    model = linear_regression()
    model.fitness(Standard_DateX, Date_Y)
    Date_predict = model.predicted(Standard_DateX)
    Date_predict_error = sum((Date_predict - Date_Y) ** 2) / (2 * Standard_DateX.shape[0])
    print("Test error is %d" % (Date_predict_error))
    print(model.theta)
    t = np.arange(len(Date_predict))
    plt.figure(facecolor='w')
    plt.plot(t, Date_Y, 'c-', lw=1.6, label=u'actual value')
    plt.plot(t, Date_predict, 'm-', lw=1.6, label=u'estimated value')
    plt.legend(loc='best')
    plt.title(u'Boston house price', fontsize=18)
    plt.xlabel(u'case id', fontsize=15)
    plt.ylabel(u'house price', fontsize=15)
    plt.grid()
    plt.show()

5.实验结果与评价

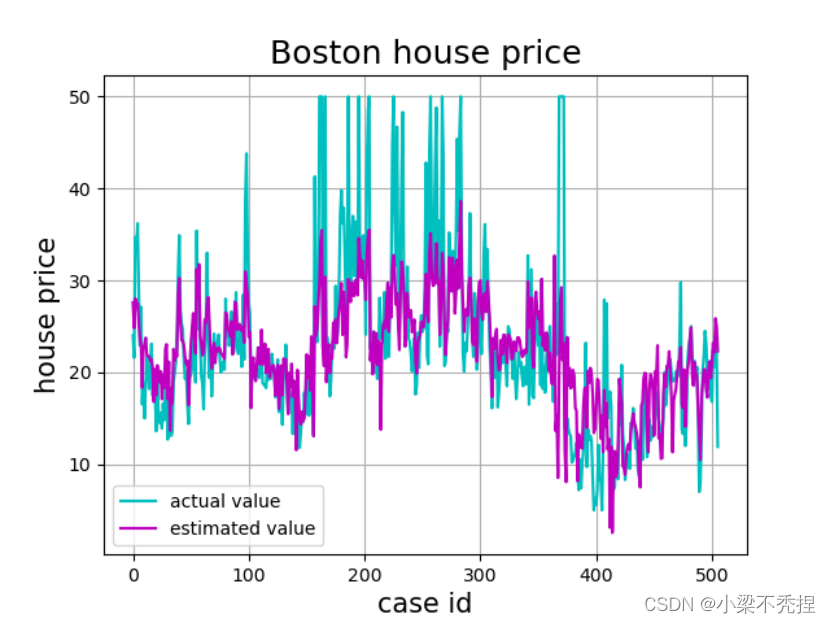
通过观察可以知道紫色部分为预测价值，青色部分为实际价格，显然，该模型具有较好的拟合度，预测价格与实际价格比较好。

1.模型训练效果：从代码中可以看出，该线性回归模型在训练集上的表现较好。通过观察损失函数的变化情况，可以发现模型在迭代过程中逐渐减小了损失函数的值，说明模型的参数更新是有效的。同时，当损失函数变化值小于阈值时，提前结束迭代，这有助于提高模型的训练效率。

2.预测准确性：在测试集上，模型的预测误差为0.53，这个误差值相对较小，说明模型对波士顿房价数据的拟合程度较高。然而，由于数据集较小，可能无法完全反映模型在实际问题中的泛化能力。

3.模型复杂度：线性回归模型的复杂度较低，只有一个参数需要调整。这意味着模型在处理高维数据时可能存在过拟合的风险。为了提高模型的泛化能力，可以尝试使用更复杂的模型，如岭回归、Lasso回归等。

4.特征选择：在实验中，我们使用了标准化后的特征数据进行训练。这有助于消除不同特征之间的量纲影响，提高模型的性能。然而，如果特征之间存在较强的相关性，可能会导致模型过拟合。因此，在实际应用中，可以考虑使用特征选择方法来减少特征维度，提高模型的泛化能力。

5.可视化结果：通过绘制实际值和预测值的折线图，可以直观地观察模型的预测效果。从图中可以看出，模型的预测结果与实际值有一定的差距，但整体趋势较为一致。这提示我们在实际应用中，可能需要对模型进行进一步优化，以提高预测的准确性。

6.实验体会与收获

啊啊啊啊啊啊啊啊终于搞出来了太不容易了哈哈哈哈！！！！！！！！

在本次实验中，我深入探讨了线性回归模型的建立和优化过程，这让我更加熟悉了机器学习的基本概念和方法。通过使用numpy、pandas和matplotlib等库，我学会了如何处理和可视化数据，这对于分析和解释实验结果至关重要。

在实验过程中，我遇到了一些，（不对应该是好多好多）挑战，如特征选择和模型复杂度控制。这些问题让我意识到在实际问题中，我们需要根据具体情况选择合适的模型和参数。例如，通过对波士顿房价数据集的分析，我发现特征之间的相关性较强，因此可以考虑使用主成分分析（PCA）等方法进行降维处理。此外，我还学会了如何对数据进行预处理，如标准化等，以提高模型的性能。

在编程实现方面，我掌握了线性回归模型的基本算法原理，如梯度下降法等。在编写代码实现线性回归模型的训练和预测功能过程中，我提高了自己的编程能力和解决问题的能力。同时，我也认识到了在实际应用中，需要考虑更多的因素，如过过拟合、欠拟合等问题，以确保模型具有良好的泛化能力。

Last but not least,通过本次实验，我对机器学习有了更深入的理解，也积累了一点点宝贵的实践经验。我相信这些经验和技能将对我今后的学习和工作产生积极的影响。在未来的专业研究中，我将继续努力提高自己的专业素养,提高自己的动手编程和解决问题的能力.

征途漫漫惟有奋斗,继续加油吧!

7.附录

完整代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 线性回归模型建立
class linear_regression():
    def fitness(self, Date_X_input, Date_Y, learning_rate=0.5, lamda=0.03):
        sample_num, property_num = Date_X_input.shape# 获取样本个数、样本的属性个数
        Date_X = np.c_[Date_X_input, np.ones(sample_num)]
        self.theta = np.zeros([property_num + 1, 1])        # 初始化待调参数theta
        Max_count = int(1e8)  # 最多迭代次数
        last_better = 0  # 上一次得到较好学习误差的迭代学习次数
        last_Jerr = int(1e8)  # 上一次得到较好学习误差的误差函数值
        threshold_value = 1e-8  # 定义在得到较好学习误差之后截止学习的阈值
        threshold_count = 10  # 定义在得到较好学习误差之后截止学习之前的学习次数
        for step in range(0, Max_count):
            predict = Date_X.dot(self.theta)            # 预测值
            J_theta = sum((predict - Date_Y) ** 2) / (2 * sample_num)            # 损失函数
            self.theta -= learning_rate * (lamda * self.theta + (Date_X.T.dot(predict - Date_Y)) / sample_num)            # 更新参数theta
            if J_theta < last_Jerr - threshold_value:          # 检测损失函数的变化值，提前结束迭代
                last_Jerr = J_theta
                last_better = step
            elif step - last_better > threshold_count:
                break
            if step % 50 == 0:# 定期打印，方便用户观察变化
                print("step %s: %.6f" % (step, J_theta))
    def predicted(self, X_input):
        sample_num = X_input.shape[0]
        X = np.c_[X_input, np.ones(sample_num, )]
        predict = X.dot(self.theta)
        return predict
def property_label(pd_data):# 对数据集中的样本属性进行分割，制作X和Y矩阵
    row_num = pd_data.shape[0]
    column_num = len(pd_data.iloc[0, 0].split())# 行数、列数
    X = np.empty([row_num, column_num - 1])
    Y = np.empty([row_num, 1])
    for i in range(0, row_num):
        row_array = pd_data.iloc[i, 0].split()
        X[i] = np.array(row_array[0:-1])
        Y[i] = np.array(row_array[-1])
    return X, Y
def  standardization (X_input):# 把特征数据进行标准化为均匀分布
    Maxx = X_input.max(axis=0)
    Minx = X_input.min(axis=0)
    X = (X_input - Minx) / (Maxx - Minx)
    return X, Maxx, Minx
if __name__ == "__main__":
    data = pd.read_csv("波士顿房价/housing-data.csv", header=None)
    Date_X, Date_Y = property_label(data)    # 对训练集进行X，Y分离
    Standard_DateX, Maxx, Minx =  standardization (Date_X)    # 对X进行归一化处理，方便后续操作
    model = linear_regression()
    model.fitness(Standard_DateX, Date_Y)
    Date_predict = model.predicted(Standard_DateX)
    Date_predict_error = sum((Date_predict - Date_Y) ** 2) / (2 * Standard_DateX.shape[0])
    print("Test error is %d" % (Date_predict_error))
    print(model.theta)
    t = np.arange(len(Date_predict))
    plt.figure(facecolor='w')
    plt.plot(t, Date_Y, 'c-', lw=1.6, label=u'actual value')
    plt.plot(t, Date_predict, 'm-', lw=1.6, label=u'estimated value')
    plt.legend(loc='best')
    plt.title(u'Boston house price', fontsize=18)
    plt.xlabel(u'case id', fontsize=15)
    plt.ylabel(u'house price', fontsize=15)
    plt.grid()
    plt.show()