扩散模型Diffusion Model与DDPM

diffusion model是2015年的一篇文章，

https://arxiv.org/pdf/1503.03585.pdf

但是2020年的DDPM之后，才开始逐渐火起来的，

https://arxiv.org/abs/2006.11239

diffusion model

最近Diffusion Model被用在于图片生成模型当中，当前很多的模型都在使用diffusion model作为生成范式，如GLIDE，DALLE2,Imagen，和一系列Image Editing方法等等）。diffusion model相对于VAE、GAN模型的优点在于，其具有更多的可能性。

为什么叫做diffusion model?

diffusion这个词来源于热力学的启发，在热力学里，如果有2个物质混合在一起，分别是高密度的和低密度的，那么高密度的物质就会扩散到低密度，比如喷了香水，随着时间的扩散，最后香水就会充斥着整个房间，最后趋向于平衡。

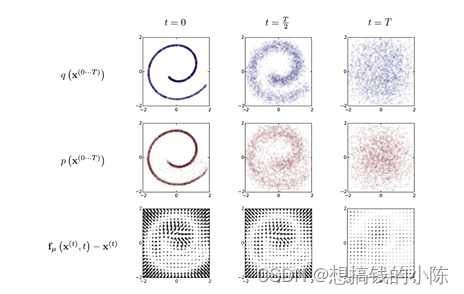
diffusion model简单理解

从概念上讲，这个diffusion model很简单，假设你有一个图片，记为X0，如下图，你每次对图像加一点噪声，加一次噪声记为Xt+1,不断对其加噪声，总共加T次以后，得到的图片基本可以说是一个噪声的图片了。我们的目标就是从噪声的图片XT，逆向扩散得到origin image,也就是X0。

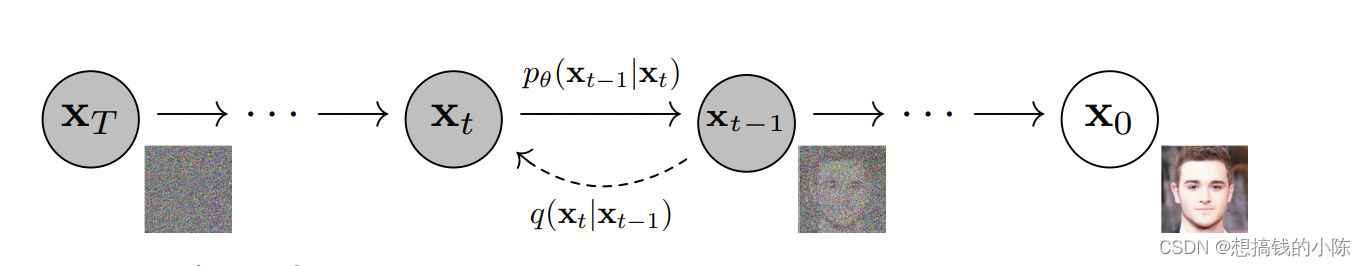
forward diffusion正向扩散过程

正向扩散过程就是我们刚才所说的，不断的朝图片加入噪声，通常初始图片我们是知道的，噪声的概率分布我们是知道的（假设服从正太分布），因此用数学公式就可以采用的个固定的markov chain形式，即逐步地向图片添加高斯噪声，每一步的图片只与上一步的图片有关：

其中

因此，模型训练就是从噪声从逆推算回初始的图像。

Reverse diffusion逆向扩散过程

我们的目标就是找到一种方式，或是训练一个网络，能够慢慢的把噪声一点一点的恢复回来。在近两年的做法当中，常见的方法是用U-net。因为reverse diffusion每次的图片的尺寸大小不变，因此U-net是一个很适合的模型。

diffusion model的小总结

这种方式可以看出，有一个致命的缺陷，就是生成模型很慢。因为每一次恢复都只能一步一步的向前恢复，而不像GAN，GAN只要训练好了这个模型，只要给他一个噪声，他就能恢复出图像，做一次的模型forward就够了。

DDPM（Denoising Diffusion Probabilistic Models）

DDPM的思想其实很简单，在reverse diffusion当中，用Xt去预测X-1的图片，但这不好优化，不去优化Xt到Xt-1的转换，而是优化Xt-1到Xt的时候，噪声是怎么加的。只去预测噪声，这有点resnet的意思，本来我们可以直接用x预测y，但直接预测y太难了，应该把其理解为y=x+residual，那我们只需要预测这个residual就可以了 。

同时DDPM还加入了time embedding，time embedding的作用就是告诉U-Net现在reverse diffusion在第几步了,这和transformer中的位置编码一样，这正余弦编码或者是一个傅里叶特征。其给模型带来的提升也是明显的。

但还有一个要加Time embeding的原因是因为，U-net是参数共享的，加入time embedding能够根据不同的输入而生成不同的输出。 我们希望在reverse diffusion的过程中，U-net能先生成一些大概的轮廓，很粗糙的coarse的图像，不需要很清晰。随着reverse diffusion往前走，当在接近还原为原来的图像的时候，我们希望能够学习到物体的边边角角的信息，一些高频信息，这样才能使输出的图片更加逼真。

具体到目标函数，那loss怎么算？

给定xt图像预测Xt-1的图像，那我们的loss就是我们已知的噪声（在前向forward是我们手工加的，所以我们是知道这个噪声的）和预测出来的噪声的差值

其中，代表我们前向forward已知的噪声，代表的是U-net神经网络，代表的是当前的输入图片，代表的是time embedding。

DDPM还有第二个贡献，就是我们只需要预测出加的噪声的均值和方差就可以了，不需要完全预测其正态分布。

------------------------------------2022.8.22补充-------------------

重参数技巧得到迭代公式

我们是如何利用重参数技巧得到每一次高斯噪声的？最开始我以为training的过程是一步一步的计算得到，例如，经过一个encoder得到,经过encoder得到，....,但后面发现不是。forward process添加的噪声是服从高斯分布变换的。这是一个以根号1-βtxt-1为均值，βt为方差的高斯分布。那forward的公式是显示的，那我们就可以直接通过x0,直接得到xt。

每次Xt加噪的公式如下：

• 表示t时刻的数据分布。
• 表示t时刻添加的高斯噪音，一般固定是均值为0方差为1的高斯分布。
• 表示当前时刻分布的均值
• 表示当前时刻分布的标准差。

因此，我们可以根据公式进行推导：

令,则

于是

...

由上，可以组成一个Xt由X0组成的式子，即

(1)

（注意一下这个公式，后面会有用到）

我们就得到了一个只与X0有关的式子。

diffusion reverse process

如果前向过程是加噪的话，逆向过程就是去噪，我们先来看看论文对逆向过程的定义：

满足高斯分布，均值为带有参数、以与为输入的，和方差（PS:这里的是一个方差符号，不是求和符号），。

我们要求出后验的扩散条件概率,这个扩散条件概率是可以用公式表达的，也就是是说，给定和，我们是可以计算出的。

我们现在开始计算。

=

                            =![\frac{q(X_{t}|X_{t-1},X_{0}) q(X_{t-1}|X_{0}))}{\frac{q(X_{t},X_{0})}{q(X_{0}}}](https://latex.codecogs.com/gif.latex?%5Cfrac%7Bq%28X_%7Bt%7D%7CX_%7Bt-1%7D%2CX_%7B0%7D%29%20q%28X_%7Bt-1%7D%7CX_%7B0%7D%29%29%7D%7B%5Cfrac%7Bq%28X_%7Bt%7D%2CX_%7B0%7D%29%7D%7Bq%28X_%7B0%7D%7D%7D)

                            =![q(X_{t}|X_{t-1})\frac{ q(X_{t-1}|X_{0})}{q(X_{t}|X_{0})}](https://latex.codecogs.com/gif.latex?q%28X_%7Bt%7D%7CX_%7Bt-1%7D%29%5Cfrac%7B%20q%28X_%7Bt-1%7D%7CX_%7B0%7D%29%7D%7Bq%28X_%7Bt%7D%7CX_%7B0%7D%29%7D)

                     

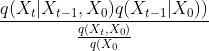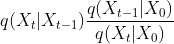
因为，和都服从高斯分布，因此正比于：

把其整理为一元二次方程的形式

这里值得注意的是，也是服从高斯分布的，因此，根据这个公式，我们可以计算出均值和方差。

因为是一个逆向的过程，我们无法知道X0，所以要把X0替换为X_t，根据上面公式1，可以得到公式

=

=

=

=

=

=

=

最后我们得到

(2)

也就是的均值，

我们总结以上的reverse diffusion process的推导，我们得到了：

csdn真的很难用，以后不用csdn了，写的全部丢失

代码

import  matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch

# TODO 实验数据
s_curve , _  = make_s_curve(10**4 , noise = 0.1)
s_curve = s_curve[:,[0,2] ]/10.0

print("shape of moons :",np.shape(s_curve))

data = s_curve.T

fig,ax = plt.subplots()
ax.scatter(*data ,color='red',edgecolor='white')
ax.axis('off')
plt.show()
dataset = torch.Tensor(s_curve).float() # shape of moons : (10000, 2)

# TODO 确定超参数的值
num_steps = 100 # 可以由beta alpha 分布 均值 标准差 进行估算

# 学习的超参数 动态的在（0，1）之间逐渐增大
betas = torch.linspace(-6,6,num_steps)
betas = torch.sigmoid(betas)* (0.5e-2 - 1e-5) + 1e-5

# 计算 alpha , alpha_prod , alpha_prod_previous , alpha_bar_sqrt 等变量的值
alphas = 1 - betas
alphas_prod = torch.cumprod( alphas ,dim=0 ) # 累积连乘  https://pytorch.org/docs/stable/generated/torch.cumprod.html
alphas_prod_p = torch.cat([torch.tensor([1]).float() ,alphas_prod[:-1]],0) # p means previous
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1-alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1-alphas_prod)

assert  alphas_prod.shape == alphas_prod.shape == alphas_prod_p.shape \
        == alphas_bar_sqrt.shape == one_minus_alphas_bar_log.shape \
        == one_minus_alphas_bar_sqrt.shape
print("all the same shape:",betas.shape)  #

# TODO 确定扩散过程中任意时刻的采样值
def q_x(x_0 ,t):
    noise = torch.randn_like(x_0) # noise 是从正太分布中生成的随机噪声
    alphas_t = alphas_bar_sqrt[t] ## 均值 \sqrt{\bar \alpha_t}
    alphas_l_m_t = one_minus_alphas_bar_sqrt[t] ## 标准差  \sqrt{ 1 - \bar \alpha_t}
    # alphas_t = extract(alphas_bar_sqrt , t, x_0) # 得到sqrt(alphas_bar[t]) ,x_0的作用是传入shape
    # alphas_l_m_t = extract(one_minus_alphas_bar_sqrt , t, x_0) # 得到sqrt(1-alphas_bart[t])
    return (alphas_t * x_0 + alphas_l_m_t * noise)

# TODO 演示原始数据分布加噪100步后的效果
num_shows = 20
fig , axs = plt.subplots(2,10,figsize=(28,3))
plt.rc('text',color='blue')
# 共有10000个点，每个点包含两个坐标
# 生成100步以内每隔5步加噪声后的图像
for i in range(num_shows):
    j = i // 10
    k = i % 10
    t = i*num_steps//num_shows # t=i*5
    q_i = q_x(dataset ,torch.tensor( [t] )) # 使用刚才定义的扩散函数，生成t时刻的采样数据  x_0为dataset
    axs[j,k].scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white')

    axs[j,k].set_axis_off()
    axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')
plt.show()

# TODO 编写拟合逆扩散过程 高斯分布 的模型
# \varepsilon_\theta(x_0,t)
import torch
import torch.nn as nn
class MLPDiffusion(nn.Module):
    def __init__(self,n_steps,num_units=128):
        super(MLPDiffusion,self).__init__()
        self.linears = nn.ModuleList([
            nn.Linear(2,num_units),
            nn.ReLU(),
            nn.Linear(num_units,num_units),
            nn.ReLU(),
            nn.Linear(num_units, num_units),
            nn.ReLU(),
            nn.Linear(num_units, 2),]

        )
        self.step_embeddings = nn.ModuleList([
            nn.Embedding(n_steps,num_units),
            nn.Embedding(n_steps, num_units),
            nn.Embedding(n_steps, num_units)
        ])
    def forward(self,x,t):
        for idx,embedding_layer in enumerate(self.step_embeddings):
            t_embedding = embedding_layer(t)
            x = self.linears[2*idx](x)
            x += t_embedding
            x = self.linears[2*idx +1](x)

        x = self.linears[-1](x)
        return x

# TODO loss　使用最简单的　loss
def diffusion_loss_fn(model,x_0,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,n_steps):# n_steps 用于随机生成t
    '''对任意时刻t进行采样计算loss'''
    batch_size = x_0.shape[0]

    # 随机采样一个时刻t,为了体检训练效率，需确保t不重复
    # weights = torch.ones(n_steps).expand(batch_size,-1)
    # t = torch.multinomial(weights,num_samples=1,replacement=False) # [barch_size, 1]
    t = torch.randint(0,n_steps,size=(batch_size//2,)) # 先生成一半
    t = torch.cat([t,n_steps-1-t],dim=0) # 【batchsize,1】
    t = t.unsqueeze(-1)# batchsieze
    # print(t.shape)

    # x0的系数
    a = alphas_bar_sqrt[t]
    # 生成的随机噪音eps
    e = torch.randn_like(x_0)
    # eps的系数
    aml = one_minus_alphas_bar_sqrt[t]
    # 构造模型的输入
    x = x_0* a + e *aml
    # 送入模型，得到t时刻的随机噪声预测值
    output = model(x,t.squeeze(-1))

    # 与真实噪声一起计算误差，求平均值
    return (e-output).square().mean()

# TODO 编写逆扩散采样函数（inference过程）
def p_sample_loop(model ,shape ,n_steps,betas ,one_minus_alphas_bar_sqrt):
    '''从x[T]恢复x[T-1],x[T-2],……，x[0]'''

    cur_x = torch.randn(shape)
    x_seq = [cur_x]
    for i in reversed(range(n_steps)):
        cur_x = p_sample(model,cur_x, i ,betas,one_minus_alphas_bar_sqrt)
        x_seq.append(cur_x)
    return x_seq

def p_sample(model,x,t,betas,one_minus_alphas_bar_sqrt):
    '''从x[T]采样时刻t的重构值'''
    t = torch.tensor(t)
    coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
    eps_theta = model(x,t)
    mean = (1/(1-betas[t].sqrt()) * (x-(coeff * eps_theta)))
    z = torch.randn_like(x)
    sigma_t = betas[t].sqrt()
    sample = mean + sigma_t * z
    return (sample)

# TODO 模型的训练
seed = 1234
class EMA():
    '''构建一个参数平滑器'''
    def __init__(self,mu = 0.01):
        self.mu =mu
        self.shadow = {}
    def register(self,name,val):
        self.shadow[name] = val.clone()

    def __call__(self, name, x): # call函数？
        assert name in self.shadow
        new_average = self.mu * x +(1.0 -self.mu) * self.shadow[name]
        self.shadow[name] = new_average.clone()
        return new_average

print('Training model ……')
'''
'''
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle = True)
num_epoch = 4000
plt.rc('text',color='blue')

model = MLPDiffusion(num_steps) # 输出维度是2 输入是x 和 step
optimizer = torch.optim.Adam(model.parameters(),lr = 1e-3)

for t in range(num_epoch):
    for idx,batch_x in enumerate(dataloader):
        loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm(model.parameters(),1.) # 
        optimizer.step()
        # for name ,param in model.named_parameters():
        #   if params.requires_grad:
        #       param.data = ems(name,param.data)

    # print loss
    if (t% 100 == 0):
        print(loss)
        x_seq = p_sample_loop(model,dataset.shape,num_steps,betas,one_minus_alphas_bar_sqrt)# 共有100个元素

        fig ,axs = plt.subplots(1,10,figsize=(28,3))
        for i in range(1,11):
            cur_x = x_seq[i*10].detach()
            axs[i-1].scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white');
            axs[i-1].set_axis_off()
            axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')