1.超图基础概念
传统的图网络结构，两点之间就可以引入一条边链接；
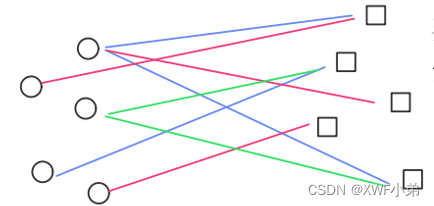
但在某些特定的领域，一条边可能链接的不止两个点，我们便引入了超图
比如：同一个班级，一个班级可以连接很多个学生；一个IP下有很多个用户，我们可以用超边来表示这个班级或这个IP；
一个超图可以拥有任意数量的节点，如果所有超边都连接两个节点那么就退化为简单图；
2.多模态的超图构建
面对多模态的场景：可以做视觉连接，文本连接和社交连接，所以将这些放入到超图结构中去解决的时候会比简单图简单很多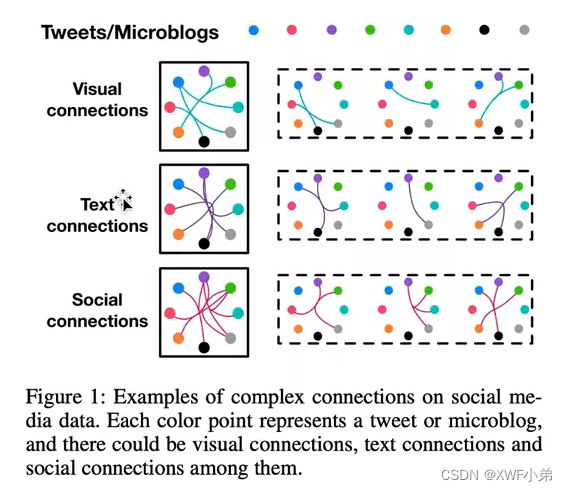
那么，多模态数据下如何构建超图如何利用算法去求得节点特征的呢？
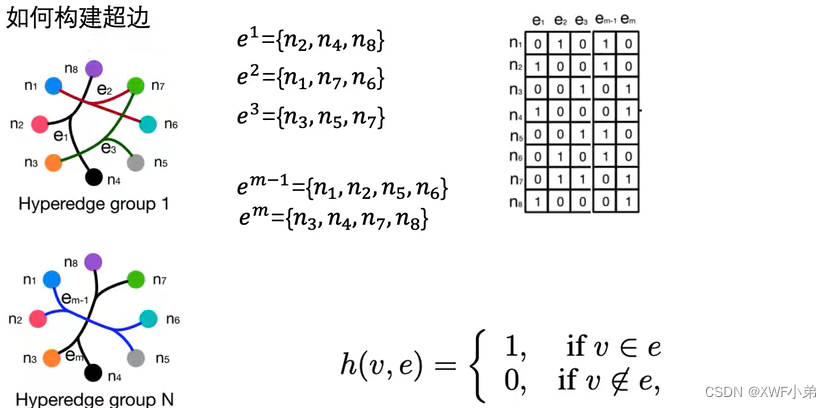
g
r
o
u
p
1
group1
group1是一个模态的超图，
g
r
o
u
p
N
group N
groupN是另一个模态的图，将多个模态拼接到一起，构建多模态超图；
超图数据形式如上图:行是超边、列是节点 ；有连接则为1，否则为0；
W是每一个超边被赋予的权值，初始化W为一个单位阵，意味着所有超边的权重都是相同的，W可以根据模型去训练，也可以固定为单位阵；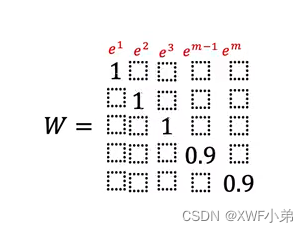
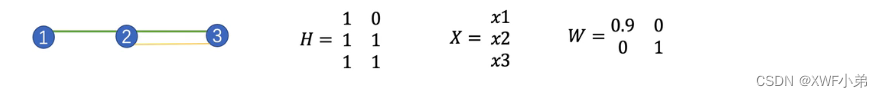
2.1节点的度：
2.2超边的度：
2.3更新公式：
GCN的更新公式：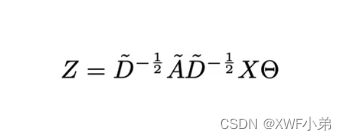
超图的更新公式：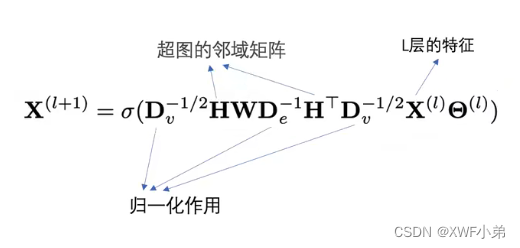
D
v
D_v
Dv是超边的度矩阵；
D
e
D_e
De是顶点的度矩阵；
W
W
W是权重矩阵；
H
H
H是超图的邻接矩阵；
X
(
l
)
X^{(l)}
X(l)是节点第L层的特征；
θ
(
l
)
\theta^{(l)}
θ(l)是全连接层；（对
X
(
l
)
X^{(l)}
X(l)进行特征转换）
举个实际的例子：
第一步：因为
θ
(
l
)
\theta^{(l)}
θ(l)是个可训练参数，先不去看
θ
(
l
)
\theta^{(l)}
θ(l)；
第二步：
D
v
−
1
/
2
D_v^{-1/2}
Dv−1/2
D
e
−
1
D_e^{-1}
De−1
D
v
−
1
/
2
D_v^{-1/2}
Dv−1/2是归一化操作也可先不看他们；
第三步：构建超边特征：
H
T
H^T
HT
X
X
X是将超边邻居节点都聚合到超边上（求和）
第四步：节点特征更新：
H
∗
H*
H∗
H
T
H^T
HT
X
X
X
第五步：利用
D
v
−
1
/
2
D_v^{-1/2}
Dv−1/2
D
e
−
1
D_e^{-1}
De−1
D
v
−
1
/
2
D_v^{-1/2}
Dv−1/2完成归一化操作；
注：需要训练的参数，前部分的时候可以把他们看成固定的值
GCN与HGNN虽然计算出来的值有一定的差别，但是他们本质上的思想是差不多的，GCN可以说是一种特殊的HGNN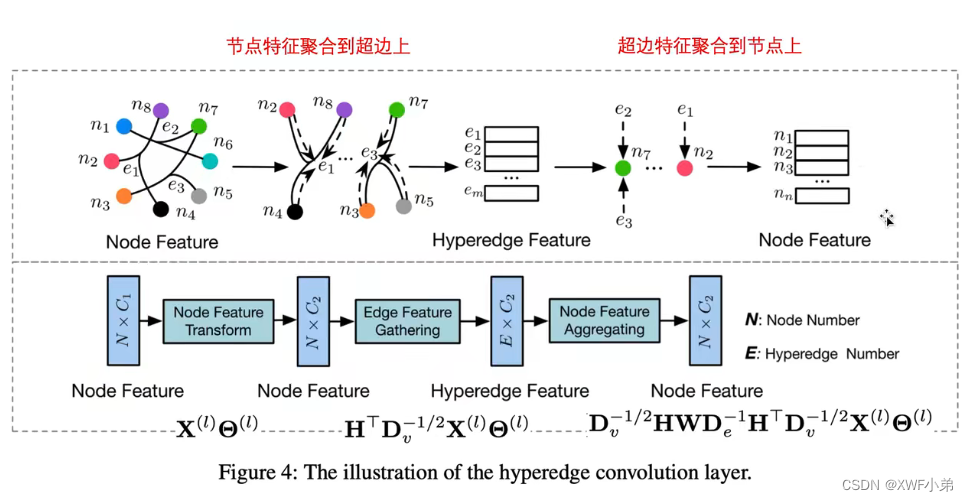
3.实验：
1.Cora引文数据集，超图结构与原始结构很相似，并没有加入更多的信息，所以效果提升的比较少；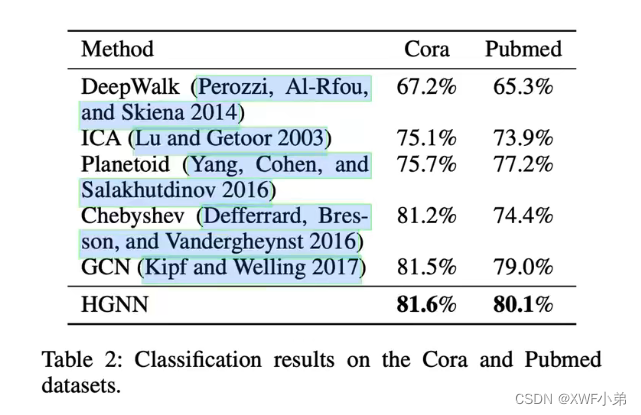
2.视觉分类任务：
本质上是一种无图结构，作者每次选择数据集的一个节点，利用其在所选特征空间中的10个最近邻生成一个包括改节点本身的超边；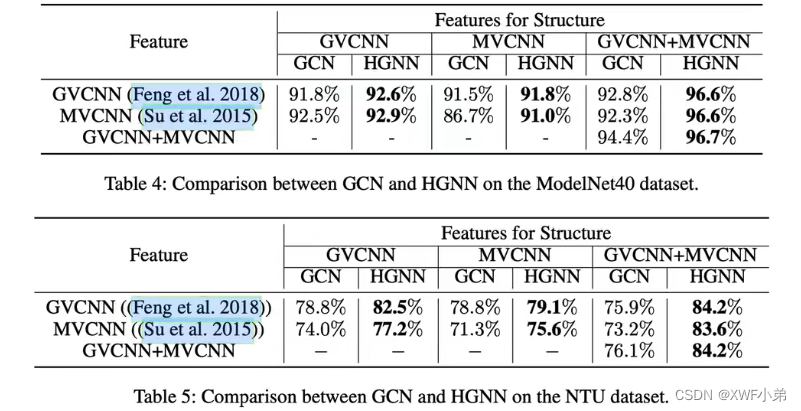
3.ModelNet40：
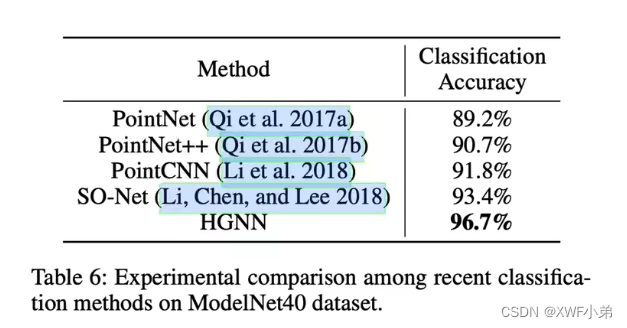
4.总结
超图结构能够表达复杂的、高阶的数据之间的相关性，与图结构或无图结构的方法相比，能更好的表示底层数据之间的关系。此外，当多模态数据\特征可用时，HGNN具有通过其灵活的超边将这些多模态信息结合在同一结构中的优势；
本文转载自: https://blog.csdn.net/weixin_45636780/article/details/128100390
版权归原作者 XWF小弟 所有， 如有侵权，请联系我们删除。
版权归原作者 XWF小弟 所有， 如有侵权，请联系我们删除。