pytorch 笔记：torch.distributions 概率分布相关（更新中）

1 包介绍

    torch.distributions包包含可参数化的概率分布和采样函数。 这允许构建用于优化的随机计算图和随机梯度估计器。

   ** 不可能通过随机样本直接反向传播。 **但是，有两种主要方法可以创建可以反向传播的代理函数。

这些是

• 评分函数估计量 score function estimato
• 似然比估计量 likelihood ratio estimator
• REINFORCE
• 路径导数估计量 pathwise derivative estimator

REINFORCE 通常被视为强化学习中策略梯度方法的基础，

路径导数估计器常见于变分自编码器的重新参数化技巧中。

    虽然评分函数只需要样本 f(x)的值，但路径导数需要导数 f'(x)。、

1.1 REINFORCE

    我们以reinforce 为例：

    当概率密度函数关于其参数可微时，我们只需要 sample() 和 log_prob() 来实现 REINFORCE：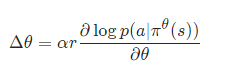

    ![](https://img-blog.csdnimg.cn/f08dc545894440bea2b9fef1ae357255.png)

    其中θ是参数，α是学习率，r是奖励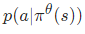，![](https://img-blog.csdnimg.cn/8e7fd858d1f54281bc124455d72cde11.png)是在状态s的时候，根据策略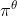![\pi^\theta](https://latex.codecogs.com/gif.latex?%5Cpi%5E%5Ctheta)使用动作a的概率

    （这个也就是policy gradient）

强化学习笔记：Policy-based Approach_UQI-LIUWJ的博客-CSDN博客

     在实践中，我们会从网络的输出中采样一个动作，在一个环境中应用这个动作，然后使用 log_prob 构造一个等效的损失函数。

     对于分类策略，实现 REINFORCE 的代码如下：（这只是一个示意代码，跑不起来的）

probs = policy_network(state)
#在状态state的时候，各个action的概率

m = Categorical(probs)
#分类概率

action = m.sample()
#采样一个action

next_state, reward = env.step(action)
#这里为了简化考虑，一个episode只有一个action

loss = -m.log_prob(action) * reward
#m.log_prob(action) 就是 logp
#reward就是前面的r
#这里用负号是因为强化学习是梯度上升

loss.backward()

2 包所涉及的类

2.1 伯努利分布

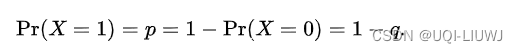
torch.distributions.bernoulli.Bernoulli(
    probs=None, 
    logits=None, 
    validate_args=None)

    创建由 probs 或 logits（但不是两者同时）参数化的伯努利分布。

    样本是二进制的（0 或 1）。 它们取值 1 的概率为 p，取值 0 的概率为 1 - p。

2.1.1 参数

probs (Number,Tensor) 采样概率**logits (Number,Tensor) 采样的对数几率

2.1.2 函数 & 属性

sample()
采样，默认采样一个值

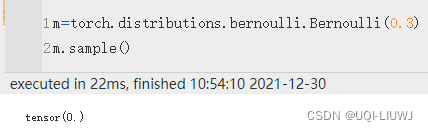
还可以按照shape 采样

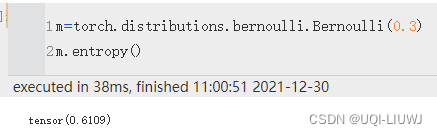
entropy

()
计算熵

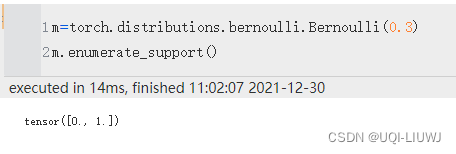
enumerate_support()
返回包含离散分布支持的所有值的张量。 结果将在维度 0 上枚举

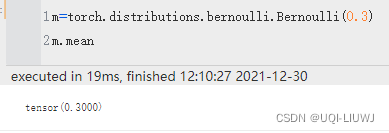
mean
均值

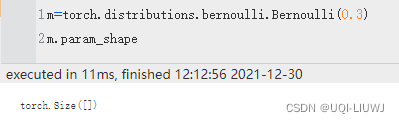
probs, logits两个输入的参数param_shape
参数的形状

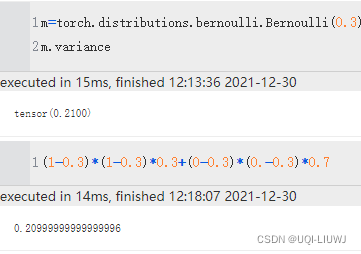
variance
方差

2.2 贝塔分布

torch.distributions.beta.Beta(
    concentration1, 
    concentration0, 
    validate_args=None)

由concentration 1 （α）和concentration 0 （β）参数化的 Beta 分布。

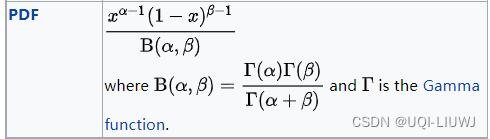
2.2.1 函数

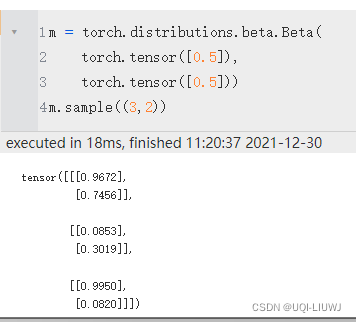
采样
默认是采样一个值，也可以设置采样的维数

entropy
计算熵

rsample

(sample_shape)
如果分布参数是批处理的，则生成一个 sample_shape 形状的重新参数化样本或 sample_shape 形状的重新参数化样本批次。

注：生成Beta分布的时候，两个参数必须至少有一个是Tensor，否则rsample效果失效

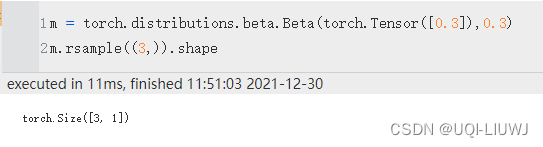
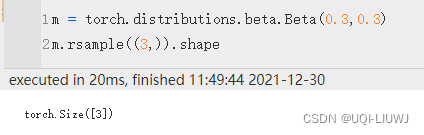
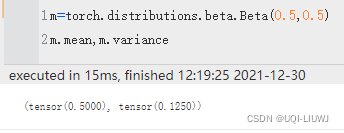
mean,variance
均值 & 方差

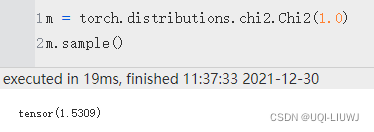
2.3 Chi2 分布

torch.distributions.chi2.Chi2(
    df, 
    validate_args=None)

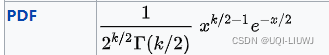
它只有sample一个函数

2.4 连续伯努利

参数和伯努利很类似

torch.distributions.continuous_bernoulli.ContinuousBernoulli(
    probs=None, 
    logits=None, 
    lims=(0.499, 0.501), 
    validate_args=None)

请注意，与伯努利不同，这里的“probs”不对应于伯努利的“probs”，这里的“logits”不对应于伯努利的“logits”，但由于与伯努利的相似性，使用了相同的名称。

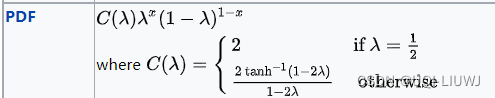
2.4.1 函数

sample还是采样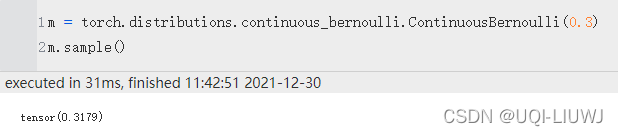cdf
返回以 value 计算的累积概率密度函数。

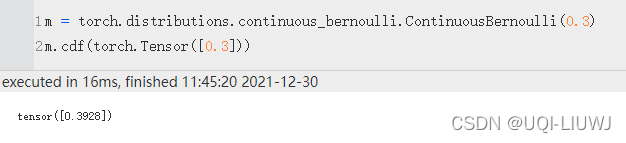
icdf
返回以 value 计算的逆累积密度/质量函数。

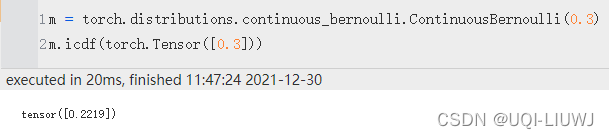
entropy
还是计算熵

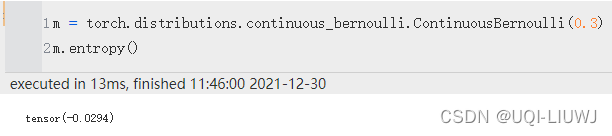
rsample
如果分布参数是批处理的，则生成一个 sample_shape 形状的重新参数化样本或 sample_shape 形状的重新参数化样本批次。

和前面Beta分布类似，只有创建时参数为Tensor，才会有rsample效果

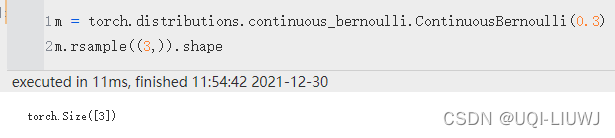
mean，variance均值 方差

2.5 二项分布

torch.distributions.binomial.Binomial(
    total_count=1, 
    probs=None, 
    logits=None, 
    validate_args=None)

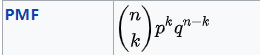
     创建由 total_count 和 probs 或 logits（但不是两者）参数化的二项分布。 total_count 必须可以用 probs/logits 广播。

2.5.1 函数&参数

sample
采样

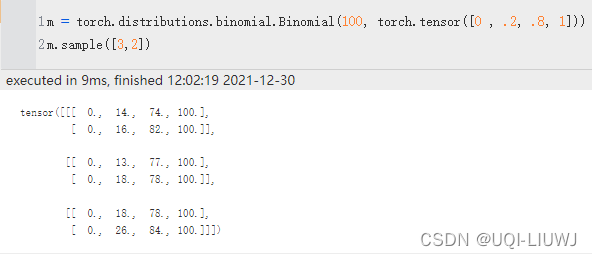
100被广播到0,0.2,0.8,1 所以每次相当于是四个二项分布
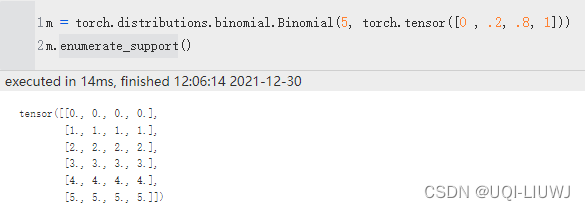
enumerate_support
返回包含离散分布支持的所有值的张量。 结果将在维度 0 上枚举

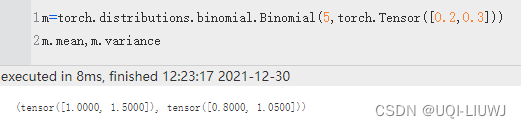
mean,variance
均值，方差

2.6 分类分布

torch.distributions.categorical.Categorical(
    probs=None, 
    logits=None, 
    validate_args=None)

样本是来{0,...,K−1} 的整数，其中 K 是 probs.size(-1)。

2.6.1 函数

sample采样

entropy

熵

enumerate_support
返回包含离散分布支持的所有值的张量。 结果将在维度 0 上枚举

2.6.2 注意：

创建分类分布时候的Tensor中元素的和可以不是1，最后归一化到1即可

import torch
import math
m=torch.distributions.Categorical(torch.Tensor([1,2,4]))
m.enumerate_support()
#tensor([0, 1, 2])

m.probs
#tensor([0.1429, 0.2857, 0.5714])

3 log_probs

很多分类都有这样一个函数log_probs，我们就统一说一下

假设m是一个torch的分类，那么m.log_prob(action)相当于

probs.log()[0][action.item()].unsqueeze(0)

（对这个action的概率添加log操作）

import torch
import math
m=torch.distributions.Categorical(torch.Tensor([1,2,4]))
m.enumerate_support()
#tensor([0, 1, 2])

a=m.sample()
a
#tensor(2)

m.probs
#tensor([0.1429, 0.2857, 0.5714])

m.probs.log()
#tensor([-1.9459, -1.2528, -0.5596])

m.log_prob(a)
#tensor(-0.5596)

m.probs.log()[a.item()]
#tensor(-0.5596)