目录
1.使数组中所有元素都等于零
1）题目描述
给你一个非负整数数组
nums
。在一步操作中，你必须：
- 选出一个正整数
x，x需要小于或等于nums中 最小 的 非零 元素。 nums中的每个正整数都减去x。
返回使
nums
中所有元素都等于
0
需要的 最少 操作数。
2）原题链接
LeetCode.6132. 使数组中所有元素都等于零
3）思路解析
( 1 ) (1) (1)很明显，贪心的思考我们应该每次选取数组中最小的非```0```元素作为```x```，然后将所有元素慢慢变为```0```。问题将变化为数组中存在多少个非```0```的**不同元素**。
4）模板代码
publicintminimumOperations(int[] nums){Set<Integer> set=newHashSet<>();int n=nums.length;for(int num : nums){if(num !=0) set.add(num);}return set.size();}
5）算法与时间复杂度
算法：贪心
时间复杂度：遍历一次数组，复杂度为
O
(
n
)
O(n)
O(n)。
2、分组的最大数量
1）题目描述
给你一个正整数数组
grades
，表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组，其中分组间的顺序满足以下全部条件：
- 第
i个分组中的学生总成绩 小于第(i + 1)个分组中的学生总成绩，对所有组均成立（除了最后一组）。 - 第
i个分组中的学生总数 小于 第(i + 1)个分组中的学生总数，对所有组均成立（除了最后一组）。 返回可以形成的 最大 组数。
2）原题链接
LeetCode.6133. 分组的最大数量
3）思路解析
( 1 ) (1) (1)后面的组不仅要保证人比前面的多，还要保证总成绩高于前面前面的组。那么很明显，我们可以**让成绩差的人去人少的组，成绩好的人去人多的组**，这样就一定能保证符合条件。然后我们以组人数分别为```1```,```2```,```3```…这样分下去，看最多能分多少组。这里相当于是一个等差数列，我们可以**二分** 出答案。
4）模板代码
publicintmaximumGroups(int[] arr){int n=arr.length;int l=0,r=100000;while(l<r){int mid=l+r+1>>1;long v=(long) mid *(mid+1)/2;if(v>n) r=mid-1;else l=mid;}return r;}
5）算法与时间复杂度
算法：贪心脑筋急转弯二分
时间复杂度：二分复杂度为
O
(
l
o
g
n
)
O(logn)
O(logn)。
3.找到离给定两个节点最近的节点
1）题目描述
给你一个
n
个节点的 有向图 ，节点编号为
0
到
n - 1
，每个节点 至多 有一条出边。
有向图用大小为
n
下标从 0 开始的数组
edges
表示，表示节点
i
有一条有向边指向
edges[i]
。如果节点
i
没有出边，那么
edges[i] == -1
。
同时给你两个节点
node1
和
node2
。
请你返回一个从
node1
和
node2
都能到达节点的编号，使节点
node1
和节点
node2
到这个节点的距离 较大值最小化。如果有多个答案，请返回
最小
的节点编号。如果答案不存在，返回
-1
。
注意
edges
可能包含环。
2）原题链接
LeetCode.6134. 找到离给定两个节点最近的节点
3）思路解析
( 1 ) (1) (1)首先很明显，答案节点必须是```node1```和```node2```都能到达的节点，我们可以对两个结点分别做一次```bfs```，把遇到的节点分别放到```set```中。( 2 ) (2) (2)使用```dist```数组统计到达每个点的距离，由于答案求的是**较大值最小化**，所以首先两个结点都能到达的结点的距离我们需要取```max```。( 3 ) (3) (3)最后对```dist```进行遍历，找到两个```set```都存储过的点，然后这些找到```dist```最小的结点。
4）模板代码
Map<Integer,Integer> map=newHashMap<>();intN=100010;int[] dist=newint[N];int ans=Integer.MAX_VALUE;Set<Integer> s1=newHashSet<>();Set<Integer> s2=newHashSet<>();int jie=-1;publicintclosestMeetingNode(int[] edges,int node1,int node2){int n=edges.length;for(int i =0; i <n; i++){add(i,edges[i]);}bfs(node1,true);bfs(node2,false);for(int i =0; i < n; i++){if(s1.contains(i)&&s2.contains(i)){if(dist[i]<ans){
ans=dist[i];
jie=i;}}}return jie;}voidbfs(int start,boolean f){Queue<Integer> q=newLinkedList<>();boolean[] st=newboolean[N];
st[start]=true;
q.offer(start);int x=0;while(!q.isEmpty()){int size=q.size();while(size-->0){int curr=q.poll();if(f) s1.add(curr);else s2.add(curr);int next=map.get(curr);
dist[curr]=Math.max(x,dist[curr]);if(next==-1||st[next])continue;
q.offer(next);
st[next]=true;}
x++;}}voidadd(int a,int b){
map.put(a,b);}
5）算法与时间复杂度
算法：BFS
时间复杂度：最坏不超过
O
(
n
)
O(n)
O(n)
4.图中最长环
1）题目描述
给你一个
n
个节点的 有向图 ，节点编号为
0
到
n - 1
，其中每个节点 至多 有一条出边。
图用一个大小为
n
下标从 0 开始的数组
edges
表示，节点
i
到节点
edges[i]
之间有一条有向边。如果节点
i
没有出边，那么
edges[i] == -1
。
请你返回图中的 最长 环，如果没有任何环，请返回
-1
。
一个环指的是起点和终点是 同一个 节点的路径。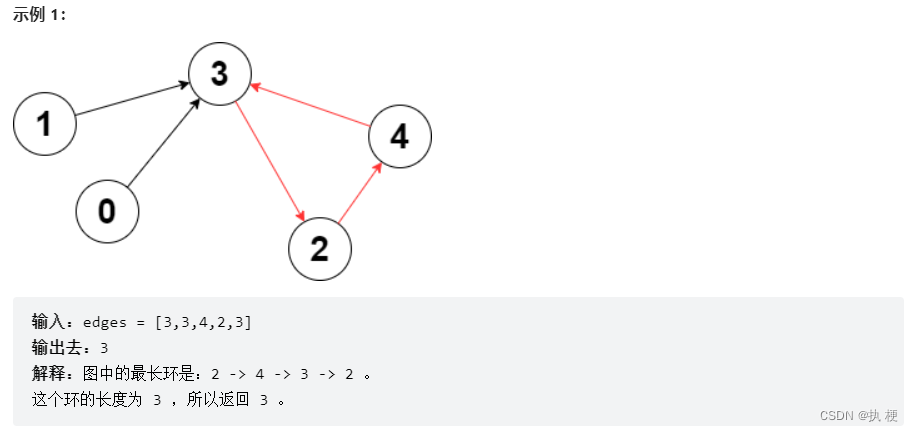
2）原题链接
LeetCode.6135. 图中的最长环
3）思路解析
( 1 ) (1) (1)找到图中最长环，我们可以对每个点进行一次搜索，在搜索的过程中，记录下到达了哪些点和到该点的距离，使用哈希存下来，当遇到走过的点说明遇到了环，算出此时的环长。( 2 ) (2) (2)由于每个点的出度都为```1```，所以对于之前已经访问过的点，我们不需要再以它为起点进行搜索了，否则会超时。在所有搜索到的环中取最大值。
4）模板代码
classSolution{boolean[] st=newboolean[100010];Map<Integer,Integer> map=newHashMap<>();int res=0;publicintlongestCycle(int[] edges){int n=edges.length;for(int i =0; i <n ; i++){add(i,edges[i]);}for(int i =0; i < n; i++){if(!st[i])bfs(i);}return res==0?-1:res;}voidbfs(int start){Queue<Integer> q=newLinkedList<>();
st[start]=true;
q.offer(start);Map<Integer,Integer> ad=newHashMap<>();
ad.put(start,0);int x=0;while(!q.isEmpty()){int size=q.size();while(size-->0){int curr=q.poll();int next=map.get(curr);if(ad.containsKey(next)){
res=Math.max(x-ad.get(next)+1,res);}if(next==-1||st[next])return;
ad.put(next,x+1);
q.offer(next);
st[next]=true;}
x++;}}voidadd(int a,int b){
map.put(a,b);}}
5）算法与时间复杂度
算法：BFS
时间复杂度：每个点最多访问一次，
O
(
n
)
O(n)
O(n)
5、周赛总结
图论题不熟练，写的太慢，代码又臭又长。
本文转载自: https://blog.csdn.net/m0_57487901/article/details/126084167
版权归原作者 执 梗 所有， 如有侵权，请联系我们删除。
版权归原作者 执 梗 所有， 如有侵权，请联系我们删除。