主成分分析（PCA）及其可视化——python

可以看看这个哦python入门：Anaconda和Jupyter notebook的安装与使用_菜菜笨小孩的博客-CSDN博客

如果你学会了python 可以看看matlab的哦

主成分分析（PCA）及其可视化——matlab_菜菜笨小孩的博客-CSDN博客

一、主成分分析的原理

    主成分分析是利用降维的思想，在损失很少信息的前提下把多个指标转化为几个综合指标的多元统计方法。通常把转化生成的综合指标称之为主成分，其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，这就使得主成分比原始变量具有某些更优越的性能。这样在研究复杂问题时就可以只考虑少数几个主成分而不至于损失太多信息，从而更容易抓住主要矛盾，揭示事物内部变量之间的规律性，同时使问题得到简化，提高分析效率。

     主成分分析正是研究如何通过原来变量的少数几个线性组合来解释原来变量绝大多数信息的一种多元统计方法。

二、主成分分析步骤

1.主成分分析的步骤：

    1.根据研究问题选取初始分析变量；

    2.根据初始变量特性判断由协方差阵求主成分还是由相关阵求主成分（数据**标准化**的话需要用系数相关矩阵，数据**未标准化**则用协方差阵）；

    3.求协差阵或相关阵的特征根与相应标准特征向量；

    4.判断是否存在明显的多重共线性，若存在，则回到第一步；

    5.主成分分析的适合性检验

    6.得到主成分的表达式并确定主成分个数，选取主成分；

    7.结合主成分对研究问题进行分析并深入研究。

2.部分说明

一组数据是否可以用主成分分析，必须做适合性检验。可以用球形检验和KMO统计量检验。（1）球形检验（Bartlett)

    球形检验的假设：

             H0：相关系数矩阵为单位阵（即变量不相关）

            H1：相关系数矩阵不是单位阵（即变量间有相关关系）

2）KMO（Kaiser-Meyer-Olkin)统计量

    KMO统计量比较样本相关系数与样本偏相关系数，它用于检验样本是否适于作主成分分析。

    KMO的值在0,1之间，该值越大，则样本数据越适合作主成分分析和因子分析。一般要求该值大于0.5，方可作主成分分析或者相关分析。

    Kaiser在1974年给出了经验原则：

            0.9以上       适合性很好

            0.8~0.9        适合性良好

            0.7~0.8        适合性中等

            0.6~0.7        适合性一般

            0.5~0.6        适合性不好

            0.5以下       不能接受的        

（3）主成分分析的逻辑框图

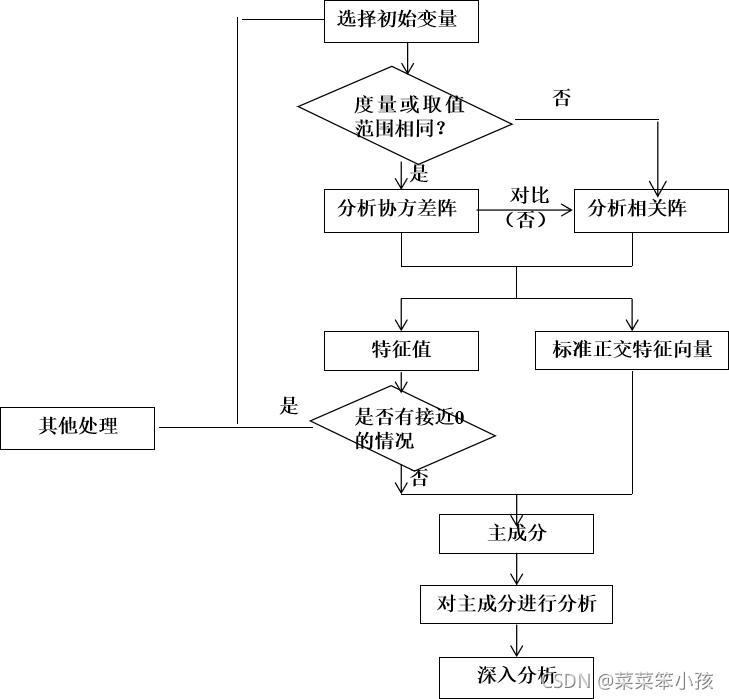
三、所用到的库 factor_analyzer库

1. pandas

pip instal  pandas

2.numpy

pip install numpy

3.matplotlib

pip install matplotlib

四、案例实战

1.数据集

数据集aa.xls - 蓝奏云 不能直接分享csv文件

2.导入库

导入数据处理和分析所需要的库：

# 数据处理
import pandas as pd
import numpy as np

# 绘图
import seaborn as sns
import matplotlib.pyplot as plt

3.读取数据集

df = pd.read_csv(r"D:\桌面\aa.csv", encoding='gbk', index_col=0).reset_index(drop=True)
df

运行结果：

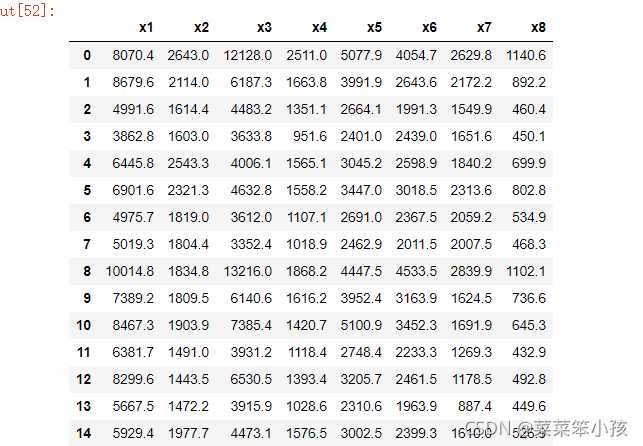
4.进行球状检验

检验总体变量的相关矩阵是否是单位阵（相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零）；即检验各个变量是否各自独立。

# Bartlett's球状检验
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(chi_square_value, p_value)

运行结果：

5.KMO检验

检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。

# KMO检验
# 检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。
# 通常取值从0.6开始进行因子分析
from factor_analyzer.factor_analyzer import calculate_kmo

kmo_all, kmo_model = calculate_kmo(df)
print(kmo_all)

运行结果：

6.求相关矩阵

（1）数据标准化做法

1.进行标准化

用到了 preprocessing 库

怎么导入：

from sklearn import preprocessing

标准化代码：

df = preprocessing.scale(df)
df

结果：

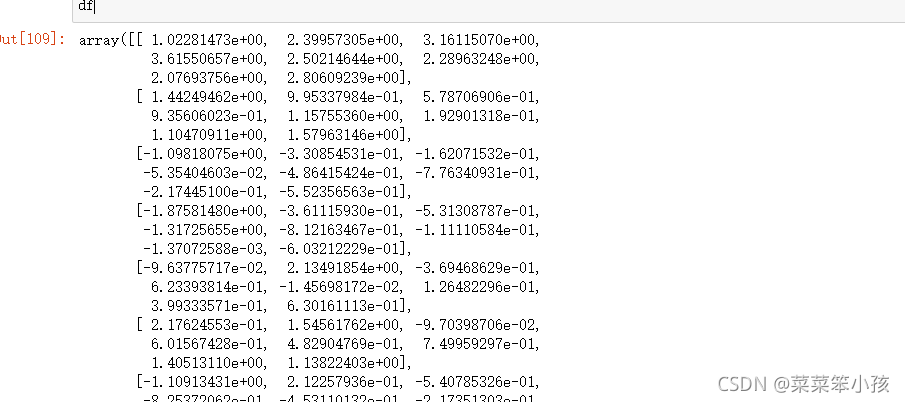
2.求相关系数矩阵

为了方面下面引用，就和协方差阵的赋值符号一样了！！

covX = np.around(np.corrcoef(df.T),decimals=3)
covX

运行结果：

3.求解特征值和特征向量

featValue, featVec=  np.linalg.eig(covX.T)  #求解系数相关矩阵的特征值和特征向量
featValue, featVec

运行结果：

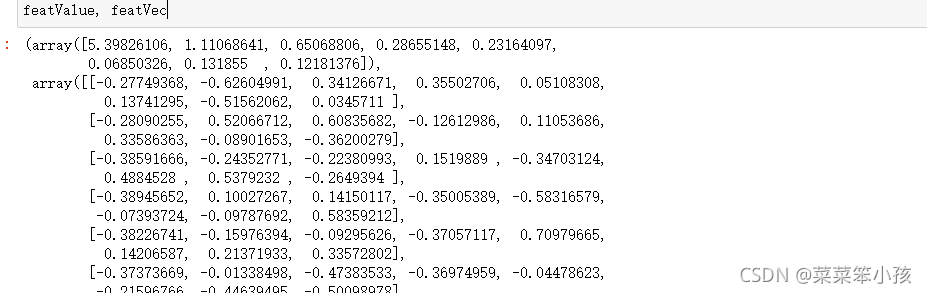
（2）数据不标准化做法

1.求均值

def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
average = meanX(df)
average

运行结果：

2.查看列数和行数

m, n = np.shape(df)
m,n

运行结果：

3.写出同数据集一样的均值矩阵

data_adjust = []
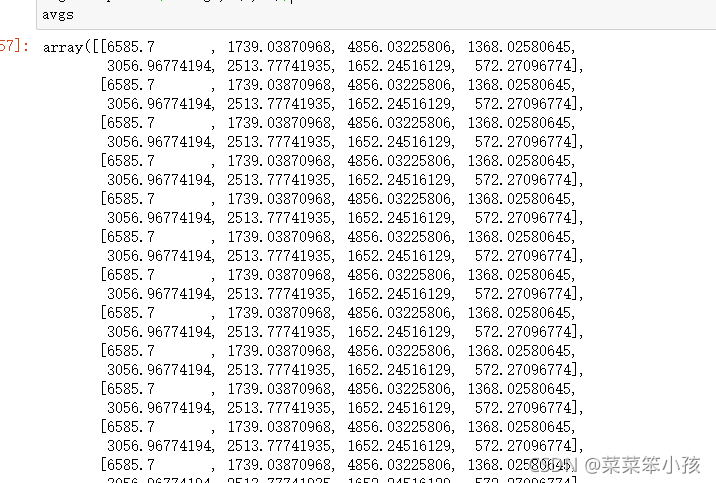
avgs = np.tile(average, (m, 1))
avgs

运行结果：

4.对数据集进行去中心化

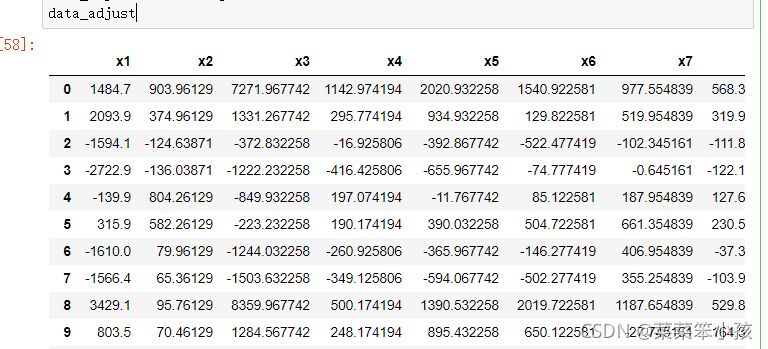
data_adjust = df - avgs
data_adjust

运行结果：

5.计算协方差阵

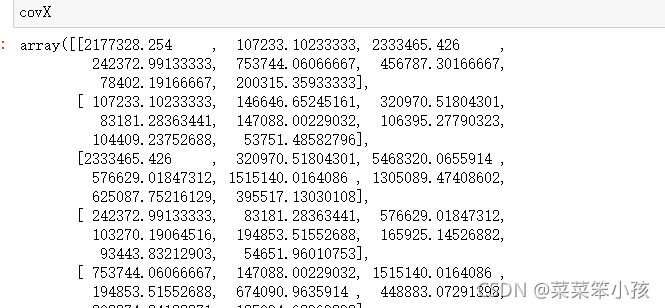
covX = np.cov(data_adjust.T)   #计算协方差矩阵
covX

运行结果：

6.计算协方差阵的特征值和特征向量

featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量
featValue, featVec

运行结果：

**下面的做法不再区分标不标准化了，你上面用哪种都行 **

在这里仅拿为标准化做法的数据进行下面操作！！！

7.对特征值进行排序并输出 降序

featValue = sorted(featValue)[::-1]
featValue

运行结果：

8.绘制散点图和折线图

# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), featValue)
plt.plot(range(1, df.shape[1] + 1), featValue)

# 显示图的标题和xy轴的名字
# 最好使用英文，中文可能乱码
plt.title("Scree Plot")  
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")

plt.grid()  # 显示网格
plt.show()  # 显示图形

运行结果：

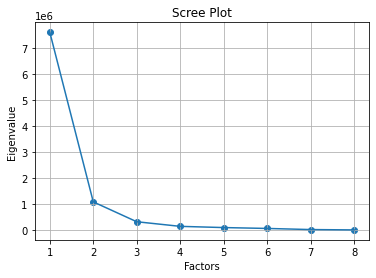
9.求特征值的贡献度

gx = featValue/np.sum(featValue)
gx

运行结果：

10.求特征值的累计贡献度

lg = np.cumsum(gx)
lg

运行结果：

11.选出主成分

#选出主成分
k=[i for i in range(len(lg)) if lg[i]<0.85]
k = list(k)
print(k)

运行结果：

12.选出主成分对应的特征向量矩阵

selectVec = np.matrix(featVec.T[k]).T
selectVe=selectVec*(-1)
selectVec

运行结果：

13.求主成分得分

finalData = np.dot(data_adjust,selectVec)
finalData

运行结果：

14.绘制热力图

# 绘图

plt.figure(figsize = (14,14))
ax = sns.heatmap(selectVec, annot=True, cmap="BuPu")

# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")

# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()

# 保存图片
# plt.savefig("factorAnalysis", dpi=500)

运行结果：

完整代码：

# 数据处理
import pandas as pd
import numpy as np

# 绘图
import seaborn as sns
import matplotlib.pyplot as plt

df = pd.read_csv(r"D:\桌面\aa.csv", encoding='gbk', index_col=0).reset_index(drop=True)
print(df)

# Bartlett's球状检验
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(chi_square_value, p_value)

# KMO检验
# 检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。
# 通常取值从0.6开始进行因子分析
from factor_analyzer.factor_analyzer import calculate_kmo

kmo_all, kmo_model = calculate_kmo(df)
print(kmo_all)

# #标准化

# #所需库
# from sklearn import preprocessing
# #进行标准化
# df = preprocessing.scale(df)
# print(df)

# #求解系数相关矩阵
# covX = np.around(np.corrcoef(df.T),decimals=3)
# print(covX)

# #求解特征值和特征向量
# featValue, featVec=  np.linalg.eig(covX.T)  #求解系数相关矩阵的特征值和特征向量
# print(featValue, featVec)

#不标准化
#均值
def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
average = meanX(df)
print(average)

#查看列数和行数
m, n = np.shape(df)
print(m,n)

#均值矩阵
data_adjust = []
avgs = np.tile(average, (m, 1))
print(avgs)

#去中心化
data_adjust = df - avgs
print(data_adjust)

#协方差阵
covX = np.cov(data_adjust.T)   #计算协方差矩阵
print(covX)

#计算协方差阵的特征值和特征向量
featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量
print(featValue, featVec)

####下面没有区分#######

#对特征值进行排序并输出 降序
featValue = sorted(featValue)[::-1]
print(featValue)

#绘制散点图和折线图
# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), featValue)
plt.plot(range(1, df.shape[1] + 1), featValue)

# 显示图的标题和xy轴的名字
# 最好使用英文，中文可能乱码
plt.title("Scree Plot")
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")

plt.grid()  # 显示网格
plt.show()  # 显示图形

#求特征值的贡献度
gx = featValue/np.sum(featValue)
print(gx)

#求特征值的累计贡献度
lg = np.cumsum(gx)
print(lg)

#选出主成分
k=[i for i in range(len(lg)) if lg[i]<0.85]
k = list(k)
print(k)

#选出主成分对应的特征向量矩阵
selectVec = np.matrix(featVec.T[k]).T
selectVe=selectVec*(-1)
print(selectVec)

#主成分得分
finalData = np.dot(data_adjust,selectVec)
print(finalData)

#绘制热力图

plt.figure(figsize = (14,14))
ax = sns.heatmap(selectVec, annot=True, cmap="BuPu")

# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")

# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()

# 保存图片
# plt.savefig("factorAnalysis", dpi=500)

总结：

几经周转终于完成了matlab和python的主成分分析，也学到了很多，也体会到了完成时的成就感

本文中遇到的问题，矩阵相乘，只能两两相乘，索引方式区别于matlab，但也有很多库类似，比如 cumsum python需调用numpy库使用，等等，如果本文有错误请大家多多指正，谢谢！！！