预测模型建模
- 时序数据的预测通常建模为利用历史数据值预测未来的数据走势。
- 简单的数学表示: x => S => x^‘ 其中: x = {x_1,x_2,…,x_t} 表示历史数据, S 表示预测系统, x^‘ 表示预测结果。
- 预测可分为短期预测(单步预测)和长期预测(多步预测)
- 短期预测的数学表示: x_{t+1}^‘ = f(x_1,x_2,…,x_t) 其中 x_{t+1}^‘ 是 t+1 时刻的预测结果,f是预测模型函数。
- 长期预测的数学表示:(x_{t+1}^‘,x_{t+1}^‘,…,x_{t+m}^‘)=f(x_1,x_2,…,x_t) 其中:x_{t+1}^‘,x_{t+2}^‘,…,x_{t+m}^‘ 表示对应时刻的预测值。
预测方法
线性预测方法
基于指数平滑的预测方法(时序数据预测早期常用的方法之一)
- 基本思想:利用权值将当期时刻的真实值和预测值联系起来,以加权算术平均数方法对预测对象进行预测。适合用来预测没有明显趋势和季节性的时间序列。
- 数学表示:x_{t+1}^‘=ax_t+(1-a)x_t^‘ 其中:a(0<a<1)表示平滑系数,x_{t+1}^‘是 t+1 时刻的预测值,x_t^‘和 x_t 分别是 t 时刻的预测值和真实值。展开上面的数学表示:x_{t+1}^‘=ax_t+a(1-a)^2x_{t-1}^‘+a(1-a)^3x_{t-3}+…+a(1-a)^{t-1}x_1 其中:a,a(1-a),…,a(1-a)^{t-1} 是数据各时刻的权值,权值距离预测时刻由近到远按指数逐级递减,即 a>a(1-a)>···> a(1-a)^{t-1}。
- 指数平滑预测法主要包括一次指数平滑法、二次指数平滑法和三次指数平滑法。
- 优点:算法实现简单,所需数据信息少,只利用历史数据的加权和就可以预测出下一时刻的数据。
- 缺点:1. 对平滑系数较为敏感,平滑系数的选择不同,预测结果不同,会影响预测精度。2. 该方法只适用于短期的预测,对于长期且不稳定的股票数据会造成严重失误。
基于自回归积分移动平均的预测方法
- 自回归积分移动平均模型(ARIMA)是自回归移动平均模型(ARMA)的扩展,自回归移动平均模型(ARMA)更加适合处理平稳的时间序列,而金融时序数据具有不平稳性,由此扩展出了自回归积分移动平均模型(ARIMA)。
- 自回归积分移动平均模型(ARIMA)由自回归模型(AR)、移动平均模型(MA)和差分法结合而出。- 自回归模型(AR)- 基本思想:描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。- 适用条件:1. 自回归模型必须满足平稳性的要求。2. 自回归只适用于预测与自身前期相关的现象。- p阶自回归过程的公式定义:y_t=u+\sum_{i=1}^pr_iy_{t-i}+e_t 其中:y_t是当前值,u是常数项,p是阶数,r_i是自相关系数,e_t是误差。- 移动平均模型(MA)- 基本思想:移动平均模型关注的是自回归模型中的误差项的累加。- 模型功能:移动平均法能有效地消除预测中的随机波动。- q阶自回归过程的公式定义:y_t=u+\sum_{i=1}^q\theta_ie_{t-i}+e_t。
- 基本思想:该方法是利用差分法经过 d 次差分将时序数据平稳化,然后确定参数 p、q 进行预测,最后将预测结果反平稳化得到最后的预测结果。
- 数学表示:x_t^‘=u+\sum_{i=1}^pr_ix_{t-i}+e_t+\sum_{i=1}^q\theta_ie_{t-i} 其中:x_t^‘表示时序数据预测值;r_i 和 \theta_i分别为 AR 和 MA 的系数;x_{t-1},…,x{t-p} 是历史数据;e_t是符合零均值白噪声序列。(白噪声表示数据之间没有相关性)
- 缺点:对于长期的预测不理想,并且这类方法对于波动较大的股票数据难以得到理想的结果。
非线性预测方法
针对时序数据中股票数据非线性及高噪声的特点,利用线性模型的预测方法对这类数据进行预测无法达到令人满意的效果。而非线性方法能够更好地捕捉股票数据的内在规律,从而得到更加准确的预测结果。
基于 BP 神经网络的预测方法
神经网络(ANN)是一种模拟人类大脑神经元连接结构进行信息处理的数学模型,它根据训练数据不断调整内部节点之间的关系学习数据变化。神经网络是一种表达能力极强的非线性模型,它的优势在于自适应性、泛化能力、容错性等方面,所以它在处理非线性数据时表现得更突出。
- 基本思想:BP 神经网络由输入层、隐藏层和输出层组成,在训练过程中分为两个过程:1. 数据输入层经隐藏层到输出层输出,即正向传播过程,模型通过正向传播进行数据预测,目标是使输出的预测值x_{t+1}^‘与实际值x_{t+1}尽可能保持一致。2. 如果输出层输出的数据没有达到预期的效果,则误差将从相反的方向对权值进行调整,即反向传播过程,目标是使总误差达到最小。误差可以表示为:E=\dfrac{1}{2}\sum_{t=1}^m(x_{t+1}-x_{t+1}^‘)
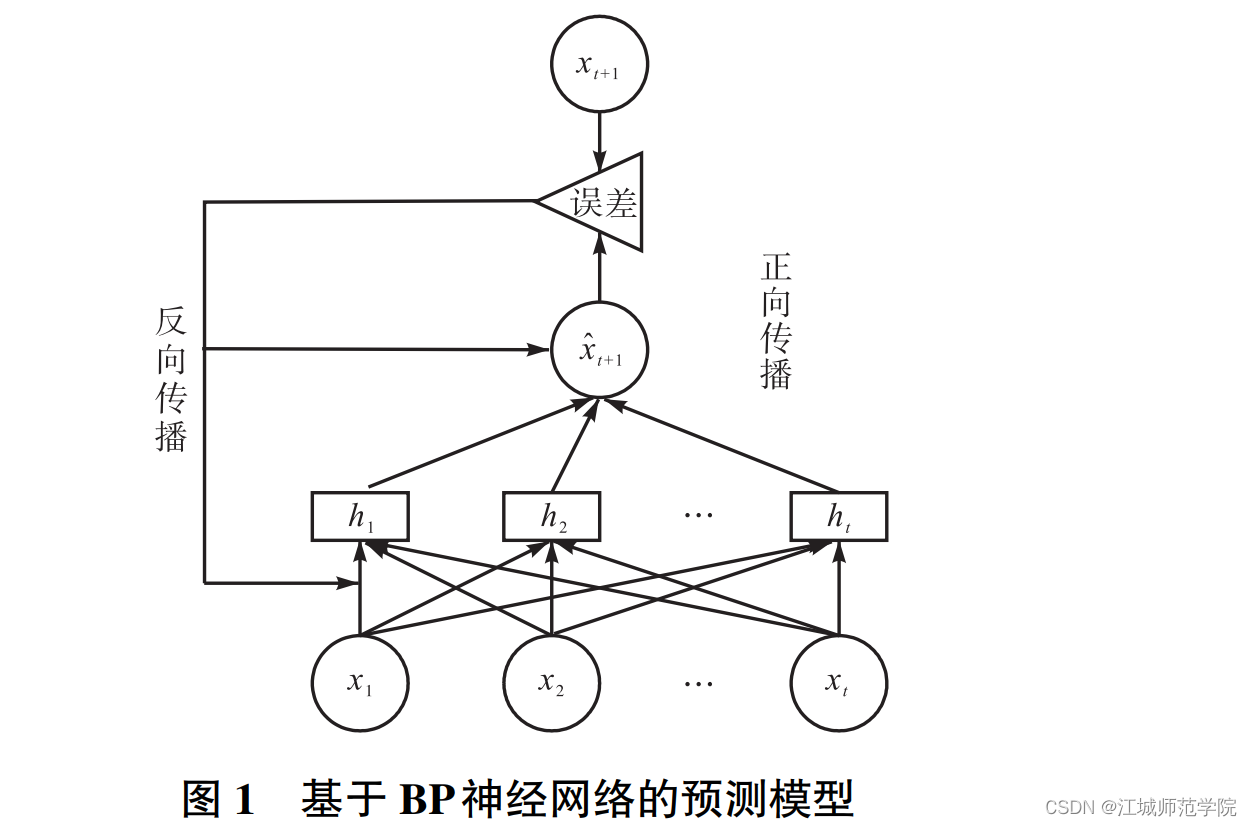 - 缺点: 1. 数据输入层经隐藏层到输出层输出,即正向传播过程。2. 如果输出层输出的数据没有达到预期的效果,则误差将从相反的方向对权值进行调整,即反向传播过程。- 对于缺点的改进方法:1. 针对训练时间长的问题,提出采用主成分分析(PCA)对输入数据进行降维,有效简化网络的输入,提高训练的速度。2. 针对容易陷入局部极小值和收敛速度慢的问题,提出在权值调整公式中加入动量项对权值调整公式进行改进,避免在训练过程中发生震荡,加快收敛速度,而且在训练时,允许略过一些极小值,这样容易陷入局部极小值的问题得到一定缓解。
- 缺点: 1. 数据输入层经隐藏层到输出层输出,即正向传播过程。2. 如果输出层输出的数据没有达到预期的效果,则误差将从相反的方向对权值进行调整,即反向传播过程。- 对于缺点的改进方法:1. 针对训练时间长的问题,提出采用主成分分析(PCA)对输入数据进行降维,有效简化网络的输入,提高训练的速度。2. 针对容易陷入局部极小值和收敛速度慢的问题,提出在权值调整公式中加入动量项对权值调整公式进行改进,避免在训练过程中发生震荡,加快收敛速度,而且在训练时,允许略过一些极小值,这样容易陷入局部极小值的问题得到一定缓解。
基于支持向量机的预测方法
- 基本思想:将输入向量以非线性的方式映射到一个高维的特征空间,在这个特征空间中构造一个决策面,利用决策面的特殊性来保持较高的泛化能力。
- 原理:找到真实值x与预测值x^‘之间的预测关系。f:R^n \rightarrow R 其中:R^n是影响数据预测的因素,x\in R^n;R是预测向量,x^‘\in R。
- 数学表示:利用核函数建安非线性的回归函数:x_t^‘=\sum_{i=1}^{t-n}(\alpha_i-\alpha_i^*)K(x_i,x_t)+b 其中:\alpha_i和 \alpha_i^*是拉格朗日乘子,K(x_i,x_t)是核函数,x_t 是影响预测的因素,x_i 是 t-n 个样本中第 i 个样本,b是阈值。
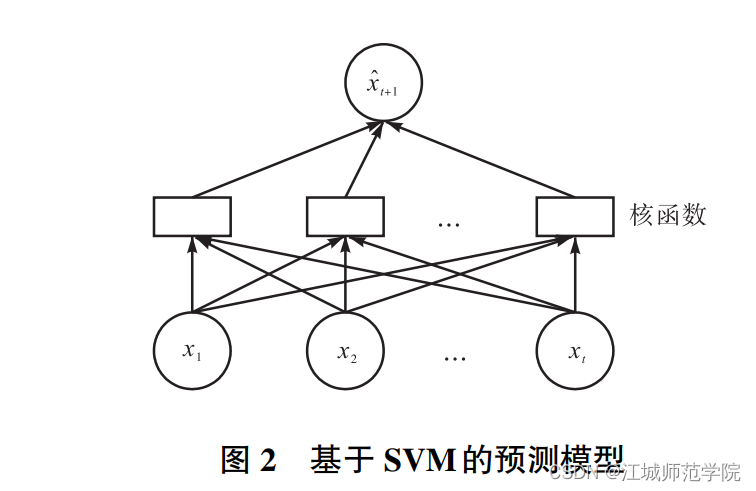 - 优点:1. 利用决策面的特殊性可以保持模型较高的泛化能力。2. 支持向量机(SVM)可以很好地处理非线性和高维的问题,克服了 BP 神经网络本身的缺陷。- 缺点:1. 支持向量机(SVM)只能得到具体的预测值,不能预测股票的变化趋势。2. 核函数的选择会对预测精度产生直接影响。- 对于缺点的改进方法:1. 针对不能预测变化趋势,提出首先使用模糊信息粒化对原始的数据进行预处理,再使用支持向量机(SVM)预测出短期的变化趋势。2. 针对核函数的选择对预测精度的影响:1. 分析采用不同的核函数对最后预测结果的影响。2. 突破传统的核函数,采用小波核将小波和支持向量机(SVM)结合,不但能消除数据的高频干扰,还具有很好的抗噪能力。3. 通过选取 3 种不同的小波核进行比较,得出不同的股票要选择合适的核函数进行预测的结论。
- 优点:1. 利用决策面的特殊性可以保持模型较高的泛化能力。2. 支持向量机(SVM)可以很好地处理非线性和高维的问题,克服了 BP 神经网络本身的缺陷。- 缺点:1. 支持向量机(SVM)只能得到具体的预测值,不能预测股票的变化趋势。2. 核函数的选择会对预测精度产生直接影响。- 对于缺点的改进方法:1. 针对不能预测变化趋势,提出首先使用模糊信息粒化对原始的数据进行预处理,再使用支持向量机(SVM)预测出短期的变化趋势。2. 针对核函数的选择对预测精度的影响:1. 分析采用不同的核函数对最后预测结果的影响。2. 突破传统的核函数,采用小波核将小波和支持向量机(SVM)结合,不但能消除数据的高频干扰,还具有很好的抗噪能力。3. 通过选取 3 种不同的小波核进行比较,得出不同的股票要选择合适的核函数进行预测的结论。
基于循环神经网络的预测方法
循环神经网络(RNN)
循环神经网络(RNN)是一种用来处理序列数据的神经网络,每一时刻输出都与历史的输入建立起关联。
- 基本思想:基于循环神经网络(RNN)的预测原理和 BP 神经网络相同,正向传播输出预测结果,反向传播进行参数优化。
- 优点:在时序数据预测应用中,循环神经网络(RNN)利用时序特性,能够很好地利用历史数据对数据未来变化作出预测。
- 缺点:循环神经网络(RNN)在训练过程中容易出现梯度消失的问题,导致在反向传播的过程中无法学习到长期依赖,它只有短期记忆,在时序数据预测中无法准确地对数据进行长期预测。
长短时记忆(LSTM)
长短时记忆(LSTM)是一种改进的循环神经网络(RNN)模型,由输入门、遗忘门、输出门和细胞单元构成。
- 基本思想:数据首先通过遗忘门,由遗忘门决定是否遗忘 t 时刻隐藏节点所包含的历史信息。在 t 时刻,将股票数据输入到输入层,然后将输入层的输出结果、t-1 时刻的隐藏层状态 h_{t-1} 和 t-1 时刻的细胞单元信息 c_{t-1} 输入到 LSTM 单元中,通过各个门及细胞单元的处理,输出数据作为下一隐藏层或输出层的输出;再经输出层的神经元输出最后的预测结果。模型通过反向传播对各个权值进行更新。
- 数学表示:f_t=\sigma(W_{xf}x_t+W_{hf}h_{t-1}+W_{cf}c_{t-1}+b_f) 其中:f_t 是遗忘门在 t 时刻的输出;\sigma是激活函数;x_t 是 t 时刻的输入;h_{t-1} 和 c_{t-1} 分别是 t-1 时刻的隐藏层状态和细胞单元信息;W_{xf}、W_{hf}、W_{cf} 是权值矩阵;{b_f}是遗忘门的偏差矩阵。
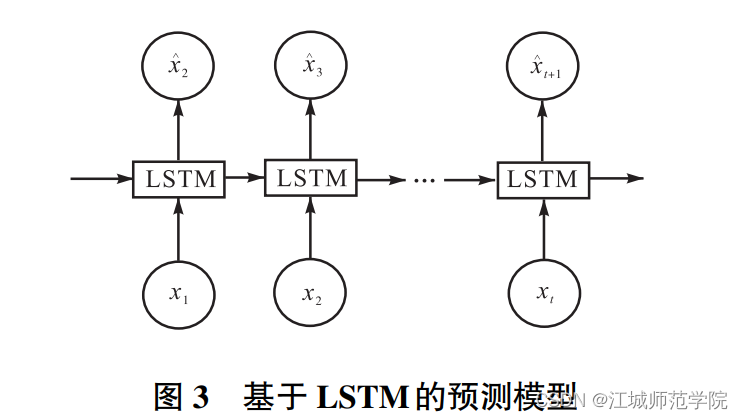 - 优点:长短时记忆(LSTM)利用特殊的门结构将短期记忆和长期记忆结合在一起,在一定程度上解决了 RNN 存在的梯度消失的问题,就能学习到长期依赖。- 缺点:1. 有陷入局部最优解的可能。2. 在预测时具有滞后性。- 对于缺点的改进方法:1. 针对局部最优解的问题,提出一种双向的 LSTM 模型可以从前后两个方向充分对股票数据之间的关系进行分析,在解决局部最优解问题的同时解决了长期依赖的问题。2. 针对预测的滞后性问题,提出运用多维度向量输入、特征工程和新闻情感分析 3 个步骤对 LSTM 进行改进,滞后性和精确度都得到一定程度的改善。- 除了改进 LSTM 本身存在的不足,还可以与其他模型组合成混合模型,提升 LSTM 的预测性能。这些混合模型和单一的模型相比更具有优势。例如:1. LSTM 和 ARIMA 组合模型2. LSTM 和卷积神经网络组合模型3. LSTM、维德情绪分析和差分隐私组合模型4. LSTM 和栈式自编码器组合模型
- 优点:长短时记忆(LSTM)利用特殊的门结构将短期记忆和长期记忆结合在一起,在一定程度上解决了 RNN 存在的梯度消失的问题,就能学习到长期依赖。- 缺点:1. 有陷入局部最优解的可能。2. 在预测时具有滞后性。- 对于缺点的改进方法:1. 针对局部最优解的问题,提出一种双向的 LSTM 模型可以从前后两个方向充分对股票数据之间的关系进行分析,在解决局部最优解问题的同时解决了长期依赖的问题。2. 针对预测的滞后性问题,提出运用多维度向量输入、特征工程和新闻情感分析 3 个步骤对 LSTM 进行改进,滞后性和精确度都得到一定程度的改善。- 除了改进 LSTM 本身存在的不足,还可以与其他模型组合成混合模型,提升 LSTM 的预测性能。这些混合模型和单一的模型相比更具有优势。例如:1. LSTM 和 ARIMA 组合模型2. LSTM 和卷积神经网络组合模型3. LSTM、维德情绪分析和差分隐私组合模型4. LSTM 和栈式自编码器组合模型
基于生成对抗网络的预测方法
生成对抗网络(GAN)是一种新型的生成模型,由生成器 G 和判别器 D 两部分组成。
- 基本思想:GAN 的主要思想就是 G 和 D 进行一个极大极小博弈游戏,其中生成器 G 用于捕捉样本数据的分布,输入随机噪声 z,目标是 生成类似真实数据的样本数据 G(z),生成的样本越 像真实数据 X 越好;判别器 D 就是一个二分器,用来 判别生成样本的真实性,输出一个概率,生成的样本 越像真实数据则输出的概率越接近 1,否则接近 0。
- 在时序数据预测中的应用:在金融时序数据预测中,该方法用生成器 G 去捕捉从金融市场中给出的历史金融数据的数据分布,并根据其分布规律对未来的数据进行预测;而判别器 D 用来判别生成金融数据的真实性。
- 数学表示:G(X)=x_{t+1}^‘ 其中:G(X)是生成器,x_{t+1}^‘是t+1时刻数据的预测值。然后将预测值x_{t+1}^‘与X={x_1,…,x_t}组合得到X^‘={x_1,…,x_t,x_{t+1}^‘},将x_{t+1}与X={x_1,…,x_t}组合得到\stackrel{\mathrm{-}}{X} = {x_1,…,x_t} ,再将两者输入到判别器D进行判别。生成器与判别器根据目标函数:\stackrel{\mathrm{min}}{G}\stackrel{\mathrm{max}}{D}V(G,D) = E[logD(\stackrel{\mathrm{-}}{X})]+E[log(1-D(X^‘))]
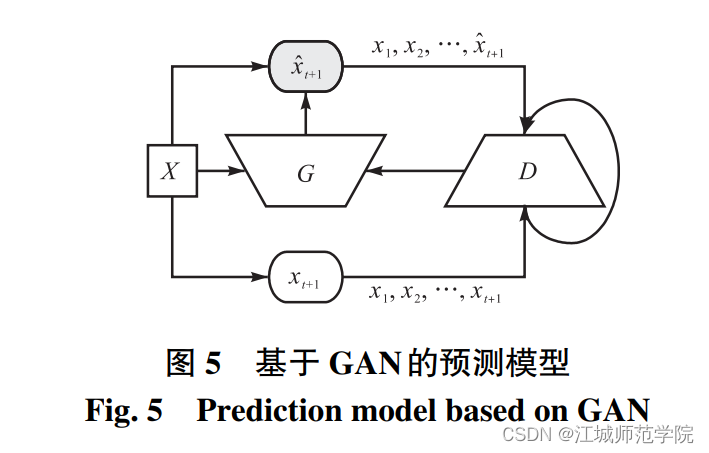 - 优点:GAN 能够更好地捕捉数据分布和反映数据的波动, 从而使得生成数据更加逼近真实数据。- 缺点:1. GAN 存在由于训练过程中出现梯度消失而导致的训练不稳定的问题。2. 生成器和判别器的选择也会对预测结果产生影响- 对于缺点的改进方法:1. Wasserstein GAN(WGAN)是对原 始 GAN 的一种改进,它使用平滑的 EarthMover(EM) 距离代替 Kullback-Leibler(KL) 和 Jensen-Shannon(JS)散度,可以一直提供有效的梯 度,从而解决梯度消失的问题,使得训练更加稳定。2. Wasserstein GAN(WGAN)是对原始 GAN 的一种改进,它使用平滑的 EarthMover(EM) 距离代替 Kullback-Leibler(KL) 和 Jensen-Shannon(JS)散度,可以一直提供有效的梯度,从而解决梯度消失的问题,使得训练更加稳定。3. 将 LSTM 作为生成器,多层感知机(multilayer percep-tron,MLP) 作为判别器对股票数据进行预测。4. 采用卷积神经网络(CNN)作为判别器。
- 优点:GAN 能够更好地捕捉数据分布和反映数据的波动, 从而使得生成数据更加逼近真实数据。- 缺点:1. GAN 存在由于训练过程中出现梯度消失而导致的训练不稳定的问题。2. 生成器和判别器的选择也会对预测结果产生影响- 对于缺点的改进方法:1. Wasserstein GAN(WGAN)是对原 始 GAN 的一种改进,它使用平滑的 EarthMover(EM) 距离代替 Kullback-Leibler(KL) 和 Jensen-Shannon(JS)散度,可以一直提供有效的梯 度,从而解决梯度消失的问题,使得训练更加稳定。2. Wasserstein GAN(WGAN)是对原始 GAN 的一种改进,它使用平滑的 EarthMover(EM) 距离代替 Kullback-Leibler(KL) 和 Jensen-Shannon(JS)散度,可以一直提供有效的梯度,从而解决梯度消失的问题,使得训练更加稳定。3. 将 LSTM 作为生成器,多层感知机(multilayer percep-tron,MLP) 作为判别器对股票数据进行预测。4. 采用卷积神经网络(CNN)作为判别器。
基于强化学习的预测方法
强化学习是机器学习领域用来解决连续决策问题的学习范式,它通过与环境的交互获得知识,自主的进行动作选择,通过不断地试错获得最优策略。
优点:自主学习能力强,能够更加适用不断变化的股市,可以更好地进行长期的交互学习。
缺点:强化学习本身存在训练困难、样本利用率低的问题。
基于强化学习的时序数据预测方法主要分为两类:1. 基于马尔科夫决策过程的时序数据预测。2. 利用强化学习对预测模型的网络结构和参数进行优化。
基于马尔科夫决策过程的时序数据预测
- 基本思想:通过状态、动作、奖励、决策等强化学习元素模拟股票价格变化的过程。
- 数学表示:M=<S,A,P,R> 其中:S是含有金融数据的状态集合;A表示动作集,由买入、卖出等交易动作组成;P表示状态转移的概率。
- 模型:1. 以马尔科夫过程为模型,使用 TD 算法2. 以马尔科夫过程为模型,使用深度 Q 网络 和 DDPG 算法
利用强化学习对预测模型的网络结构和参数进行优化
- 基本思想:预测系统对输入的数据进行处理,然后强化学习模块对其输出进行评价,随后反馈给预测系统对其进行调整或优化。
- 模型:1. 强化学习 BP 神经网络(RBP)- 基本思想:用强化学习对 BP 神经网络进行参数优化,从而实现股票预测,该模型在实现系统自我学习的同时还提高了预测精度。2. 将强化学习加入到 GAN 中- 基本思想:不断对其超参数进行优化,解决了由于股市的不断变化所导致模型无法自适应的问题。
模型评估方法
提高模型的预测精度方法:在模型进行训练之前对数据进行归一化处理,经典的归一化方法是 0 均值归一化方法。
0 均值归一化方法
- 基本思想:将原始数据减去均值再除以标准差,经过该方法处理的数据符合标准正态分布,x^‘ ~ N(0,1)
- 数学表示:x^‘=\dfrac{x-u}{r} 其中:x 是原始数据;u 是数据的均值;r 是所有数据的标准差;x^‘ 是归一化后的数据
评价指标
- 时序数据预测任务的目标是希望预测数据与真实历史数据之间的误差尽可能小。
- 均分误差(MSE)可以很好地衡量整个模型最后的训练结果,利用 MSE 定义模型的损失函数,loss=\dfrac{1}{N}\sum_{t=1}^N(x_t^‘ - x_t)^2 其中:N 表示数据预测共有 N 个时刻;x_t^‘ 是 t 时刻的数据预测值;x_t是 t 时刻数据的真实值。
- 平均绝对误差(MAE)MSE=\dfrac{1}{N}\sum_{t=1}^N|x_t^‘ - x_t| 。
- 均方根误差(RMSE)RMSE = \sqrt{\dfrac{1}{N}\sum_{t=1}^N(x_t^‘-x_t)^2}
- 平均绝对百分比误差(MAPE) MAPE = \dfrac{1}{N}\sum_{t=1}^N\dfrac{|x_t^‘-x_t|}{x_t}
- MAE、RMSE 和 MAPE 的值越小则表示预测值和真实值之间的误差越小,模型的预测效果越好。
未来的研究方向
- 数据特点来看,数据维度高、非线性。线性降维无法很好地捕捉股票数据之间的关系,对于股票数据的特征描述具有一定的局限性。如何在低维空间对股票数据进行有效分析及预测是亟待解决的研究问题。
- 从预测模型分析,将不同的方法进行组合可以取得更优的预测结果。将不同的模型及学习方法进行组合,让不同的理论方法相结合,达到优劣互补的目的。
- 使用元学习一次训练多支股票,当面对新的预测任务时可以快速地完成预测,避免重新训练模型。(迁移学习)。
欢迎大家给我指出问题,或者指明学习方向!!!
版权归原作者 江城师范学院 所有, 如有侵权,请联系我们删除。