softmax回归与交叉熵损失

前言

回归与分类是机器学习中的两个主要问题，二者有着紧密的联系，但又有所不同。在一个预测任务中，回归问题解决的是多少的问题，如房价预测问题，而分类问题用来解决是什么的问题，如猫狗分类问题。分类问题又以回归问题为基础，给定一个样本特征，模型针对每一个分类都返回一个概率，于是可以认为概率最大的类别就是模型给出的答案。但有时模型给出的每一类的概率并不满足概率的公理化定义，这时就要用到softmax回归。交叉熵是分类问题中的一个常用损失函数，本文也略有介绍。

一、softmax回归是什么？

分类问题虽然要的只是“是什么”的答案，但所使用的模型给出的每一类别的概率仍然是数值，这是一种“软分类”。

假设某一问题中有三个给定类别，每一个样本有四个特征，我们首先搭建一个有四个输入三个输出的简单神经网络模型。

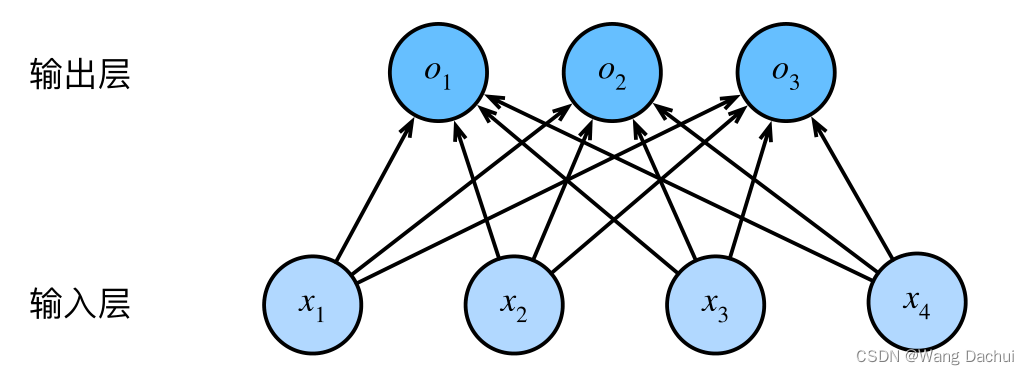
模型所表示的数学表达式为

$\begin{bmatrix} o_{1}\\o_{2} \\ o_{3}\end{bmatrix}=\begin{bmatrix} \omega _{11} & \omega _{12} & \omega _{13} & \omega _{14} \\ \omega _{21} & \omega _{22} & \omega _{23} & \omega _{24} \\ \omega _{31} & \omega _{32} & \omega _{33} & \omega _{34} \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}+\begin{bmatrix} b_{1}\\ b_{2}\\ b_{3} \end{bmatrix}$

给定一个样本，计算出 $o_{1},o_{2},o_{3}$ 之后，选取其中最大值所属的类别，作为模型给出的预测值。这样就会存在一个问题，这里的 $o$ 都是未规范化的，不满足概率的基本公理，不能直接将其视为概率。社会科学家邓肯·卢斯于1959年在选择模型（choice model）的理论基础上发明的softmax函数正好解决了这一问题。该函数实现了这样一种作用：将分类模型的输出概率规范化并保持可导。函数对向量 $\textbf{o}$ 的操作也非常简单：

$\hat{\mathbf{y}}=softmax(\mathbf{o})$ 其中 $\hat{y_{j}}=\frac{exp(o_{j})}{\sum _{k}exp(o_{k})}$

为什么使用指数函数呢？我个人的理解是，指数函数可以保证非负、可导，形式简单，完美符合概率公理，还能保证概率的大小顺序始终不变。

二、交叉熵损失是什么？

1.损失函数

在机器学习模型中，想要衡量模型好坏，就需要一个指标，损失函数所完成的就是这个任务。模型给出的答案和正确答案之间存在偏差，已经定义好的损失函数接受这两个答案，输出一个指标，模型根据这个指标才能更好地进行参数更新。有点像考试做题，老师判卷后会给你一个分数，我们根据分数和卷子再来决定如何查漏补缺。

举一个损失函数的简单例子：

$l=loss(\hat{y},y)=\hat{y}-y$

预测值比真实值高了，模型就想办法改参数让 $l$ 的值更小一点。用的指标叫损失函数，想的办法叫优化算法。这个例子过于简单以至于不怎么好用。于是人们想出了五花八门有更好性质的损失函数。比如加个绝对值或者平一下方等操作。

2.熵是什么？

熵在多个学科中都有定义，这里的熵是信息论中的熵。

信息论认为数据中的信息是可以量化的，一系列事件组成一个概率分布P，每个事件都对应一个发生的概率，那么根据公式可以计算出该分布P的熵。

$H[P]=\sum _{j}-P(j)logP(j)$

其中如果以2为底，熵的单位是比特（bit），以 $e$ 为底单位则是纳特（nat）。

这个公式有什么意义呢？

显然，如果一个事件必然发生，那么在分布P中该事件对应的概率是1，代入公式可得分布P的熵就是0。这意味着分布P中没有任何有用的信息，不用猜就知道某个事件必然会发生。但如果是一个 $(\frac{1}{2},\frac{1}{2})$ 的分布，计算其熵为log2，如果以2为底，那么信息熵是1bit，即用一位二进制代码就可以表示事件的信息。随机变量越不确定，越需要大的信息量确定其值。因此熵表示了分布的不确定性。