ROC曲线和曲线下面积AUC被广泛用于评估二元分类器的性能。但是有时,基于精确召回曲线下面积 (AUPRC) 的测量来评估不平衡数据的分类却更为合适。
本文将详细比较这两种测量方法,并说明在AUPRC数据不平衡的情况下衡量性能时的优势
预备知识——计算曲线
我假设您熟悉准确率和召回率以及混淆矩阵的元素(TP、FN、FP、TN)这些基本知识。如果你不熟悉可以搜索我们以前的文章。
现在,让我们快速回顾一下 ROC 曲线和 PRC 的计算。
假设我们有一个二元分类器来预测概率。给定一个新的例子,它输出正类的概率。我们取一个包含 3 个正例和 2 个负例的测试集,计算分类器的预测概率——在下图中按降序对它们进行排序。在相邻的预测之间,放置一个阈值并计算相应的评估度量,TPR(相当于Recall)、FPR和Precision。每个阈值代表一个二元分类器,其预测对其上方的点为正,对其下方的点为负——评估度量是针对该分类器计算的。

图 1:在给定概率和基本事实的情况下,计算 ROC 曲线和 PRC。这些点按正类概率排序(最高概率在顶部),绿色和红色分别代表正标签或负标签。
我们可以绘制 ROC 曲线和 PRC:

图 2:根据图 1 中描述的数据绘制 ROC 曲线和 PRC。
计算每条曲线下的面积很简单——这些面积如图 2 所示。AUPRC 也称为平均精度 (AP),这是一个来自信息检索领域的术语(稍后会详细介绍)。
在 sklearn 中,我们可以使用 sklearn.metrics.roc_auc_score 和 sklearn.metrics.average_precision_score。
比较 ROC-AUC 和 AUPRC
让我们直接跳到结果,然后讨论实验。
在图 3 中(下图),我们看到两个强大的模型(高 AUC),它们的 AUC 分数差异很小,橙色模型略好一些。
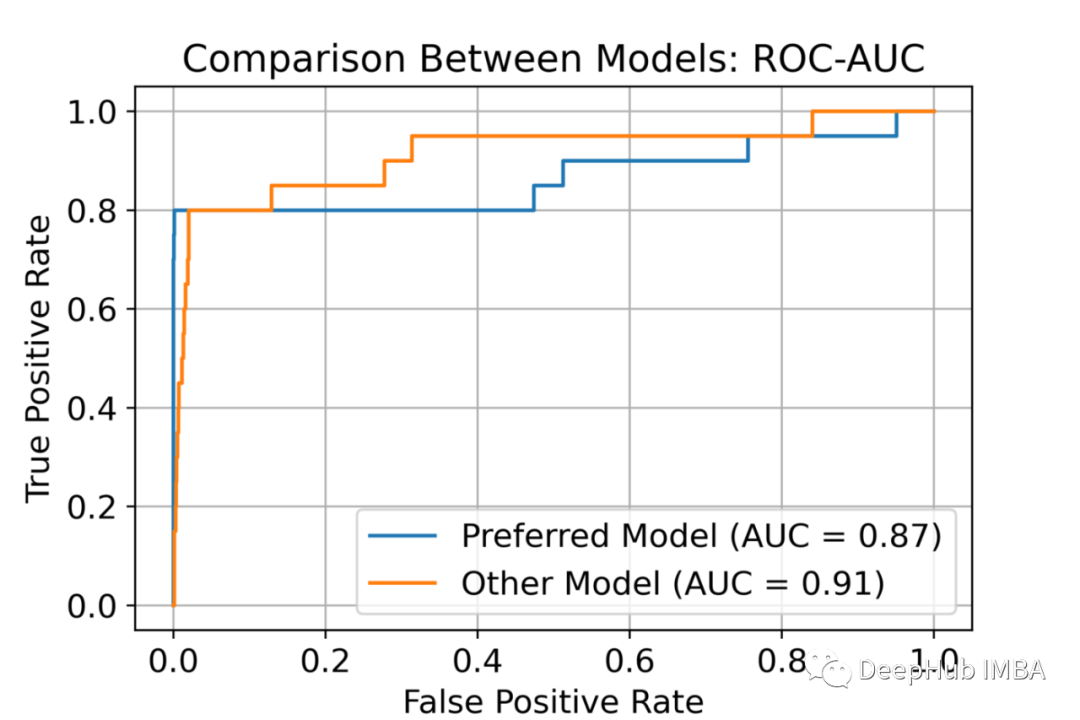
图 3:两个看似相似的模型,其中橙色的模型(“其他模型”)显示出轻微的优势。
然而,在图 4 中(下图),情况完全不同——蓝色模型要强得多。

图 4:两种模型,其中蓝色具有显着优势。
这是为什么呢? 在回答这些问题之前,让我们描述一下我们的实验。
这里的关键是类标签的分布:
- 20个正例
- 2000个负例
这是一个严重的不平衡的数据集。我们的两个模型是使用这些数据进行的预测。第一个模型在其前 20 个预测中找到 80% 的正确值·,第二 个模型在其前 60 个预测中找到 80% 的正确值·,如下图 5 所示。其余的正确预测平均分布在 剩下的样本中。

图 5:图 3 和图 4 中考虑的模型的前 100 个预测。
换句话说,模型之间的区别在于它们发现正确值的速度有多“快”。让我们看看为什么这是一个重要的属性,以及为什么 ROC-AUC 无法捕捉到它。
解释差异
ROC 曲线的 x 轴是 FPR。在给定不平衡数据的情况下,与召回率的变化相比,FPR 的变化是缓慢的。这个因素导致了上面差异的产生。
在解释之前,我们要强调的是这里是不平衡的数据集。查看 100 个示例后考虑 FPR,可能会看到最多 100 最少 80 个 的负例(误报),因此 FPR 在区间 [0.04, 0.05] 内。相比之下,我们的模型在 100 个示例中已经实现了 80% 的召回率,召回率几乎没有提高空间,这会导致 AUC 很高。
另一方面,对于PRC来说,获得误报会产生显着影响,因为每次我们看到一个误报时,精度都会大大降低。因此,“其他模型”表现不佳。但是为什么这里使用精度呢?
对于欺诈检测、疾病识别和YouTube视频推荐等任务。它们有着类似的数据不平衡的本质,因为正样本很少。如果我们模型的用户能更快地找到他们需要结果就能节省很多时间。也就是说,正样本的分数是关键。而AUPRC正好捕获了这一需求,而ROC-AUC没有做到这一点。
ROC-AUC 具有很好的概率解释([2] 中提到了其他等效解释,[4] 或 [5] 中提供了证明)。
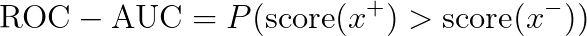
ROC-AUC 是“均匀抽取的随机正例比均匀抽取的随机负例得分更高的概率”。
对于上述严重的数据不平衡的数据集,当我们统一绘制一个随机负样本时,因为数据的不平衡,负样本更容易收集,所以我们无法确认这个负样本的有效性,但是得分确很高。但是当我们统一绘制一个随机正样本时,这个分数对我们很重要,但是分数却很低,即上述概率会很高。
对于不平衡的数据我们高兴取得是,正例(数据量少的)是如何得分的而不是负例(数据量大的),ROC-AUC 不区分这些,但 AUPRC 却很敏感。
对不平衡数据的分类可能被视为一个积极的检索任务(例如,Web 文档检索),在这种情况下我们只关心来自我们的分类器(或排名器)的前 K 个预测。测量 top-K 预测通常使用平均精度 (AUPRC) 来完成,因为它是评估通用检索系统的最先进的测量方法 [3]。因此如果你发现你的不平衡任务类似于检索任务,强烈建议考虑 AUPRC。
总结
尽管 ROC-AUC 包含了许多有用的评估信息,但它并不是一个万能的衡量标准。我们使用 ROC-AUC 的概率解释进行了实验来支持这一主张并提供了理论依据。AUPRC 在处理数据不平衡时可以为我们提供更多信息。
总体而言,ROC 在评估通用分类时很有用,而 AUPRC 在对罕见事件进行分类时是更好的方法。
如果你对本文的计算感兴趣,请看作者提供的源代码:
https://github.com/1danielr/rocauc-auprc
引用
- Davis, Jesse, and Mark Goadrich. “The relationship between Precision-Recall and ROC curves.” ICML. 2006.
- https://stats.stackexchange.com/questions/132777/what-does-auc-stand-for-and-what-is-it
- Buckley, Chris, and Ellen M. Voorhees. “Evaluating evaluation measure stability.” ACM SIGIR Forum. 2017.
- https://stats.stackexchange.com/questions/180638/how-to-derive-the-probabilistic-interpretation-of-the-auc
- https://stats.stackexchange.com/questions/190216/why-is-roc-auc-equivalent-to-the-probability-that-two-randomly-selected-samples
作者:Daniel Rosenberg