DNN（全连接神经网络）

一.

DNN网络一般分为三层

1.输入层

2.隐藏层

3.输出层

简单网络如下：

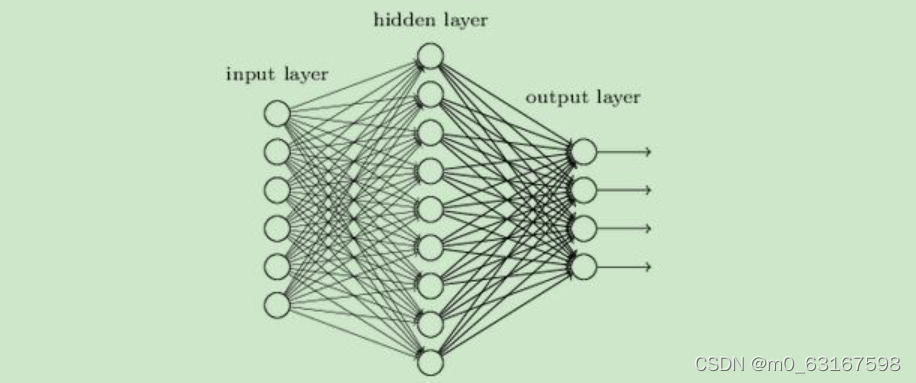
二.前向传播

从第二层开始，每一个神经元都会获得它上一层所有神经元的结果。即每一个 y = wx + b的值。

具体分析如下：

如此下去就会非常可能出现了一个问题------就是越靠后的神经元获得的y值会非常大，试想一下，如果这个数远远大于它前面神经元的值，前面神经元对整个网络的表达就显得毫无意义。所以我们在每创建一层网络时就要多“y”进行一次约束。

我们有很多选择，但最好的方法就是运用Sigmoid函数。它可以将每层网络中的神经元全部控制在0-1之间。

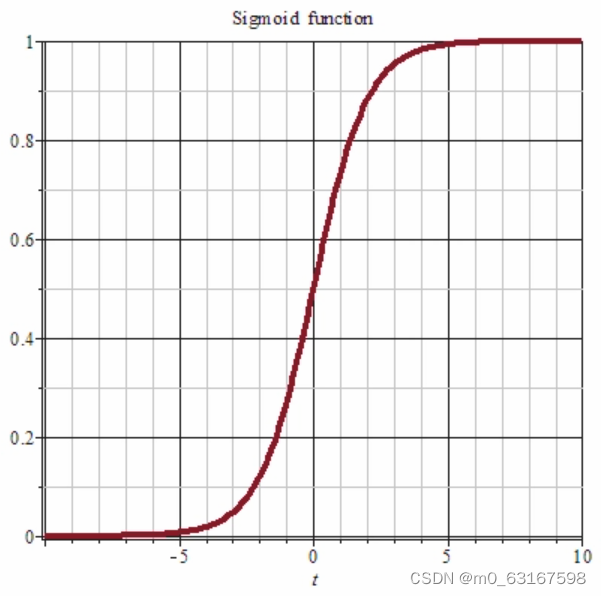
我们到最后输出层每个神经元就可以获得一个y值。

利用tensorflow所构建网络的代码如下：

model = Sequential([
    layers.Dense(256, activation=tf.nn.sigmoid),
    layers.Dense(128, activation=tf.nn.sigmoid),
    layers.Dense(64, activation=tf.nn.sigmoid),
    layers.Dense(32, activation=tf.nn.sigmoid),
    layers.Dense(10)
])

三.反向传播（数据一层层传播来，我们就一层层给它们每个反馈）

写到这里，我觉的我们可以先返回到我们出发点，我们为什么想要搭建一个网络，我相信大部分人的出发点就是想要网络对未知物体进行预测。反向传播所做的就是让每一个神经元都拥有一个w,h值。这样我们在传进一个新的数据时，我们可以将他准确的预测。
Here we go!!!!!

训练的目的是希望神经网络的输出和真实数据的输出＂一样＂，但是在＂一样＂之前，模型输出和真实数据都是存在一定的差异，我们把这个＂差异＂作这样的一个参数ee代表误差的意思，那么模型输出加上误差之后就等于真实标签了，作：y=wx+b+e。我们把每次的失误都加起来。为了防止e值的正负抵消。我们取其平方值。这样我们就可以获得一个损失函数。如下：

                       ​​​​​  ![](https://img-blog.csdnimg.cn/ca7995231916497492a66b99ee2741c4.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5oOz6KaB55yL6L-H5rW3,size_14,color_FFFFFF,t_70,g_se,x_16)

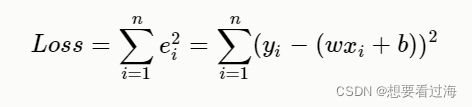
我们将损失函数（Loss）展开：

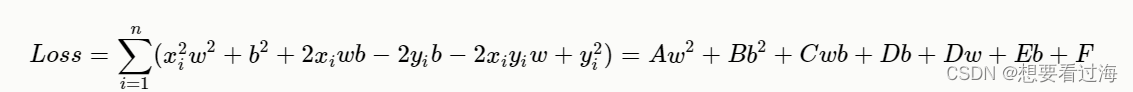
根据展开式作图：

            ​​   ![](https://img-blog.csdnimg.cn/2d4908e744404f9695a8ea049748a9ad.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5oOz6KaB55yL6L-H5rW3,size_16,color_FFFFFF,t_70,g_se,x_16)

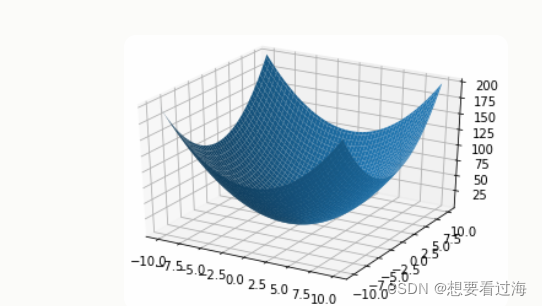
损失值顾名思义，它就是误差，我们肯定希望它越小越好，所以我们接下来想做的就是取得的新w值与b值使随时函数取得的值越小越好。专家们名其曰：梯度下降。

数学公式如下：

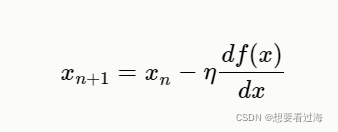
我们可以利用此公式延申到我们计算w,b上

写出总式子： ​​​​​​​ ​​​​​​​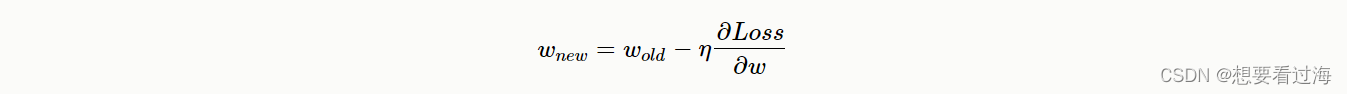

带入loss函数：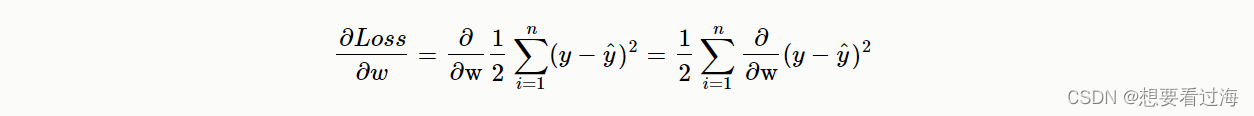

利用复合函数：

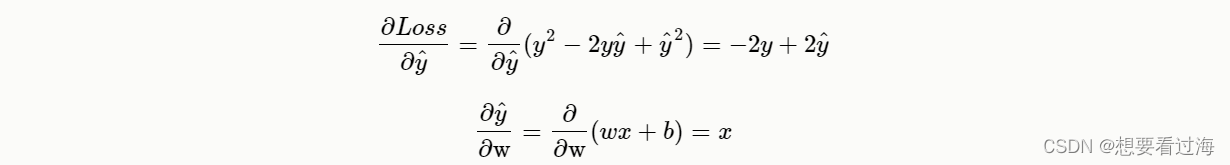
最终可以获得：

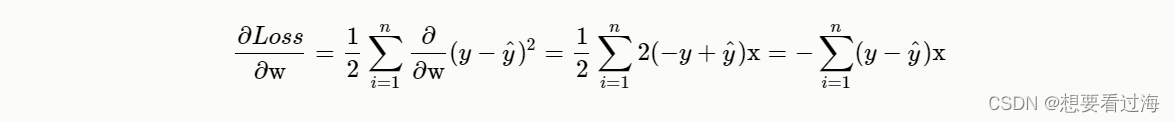
这样我们就可以获得一个线性关系：

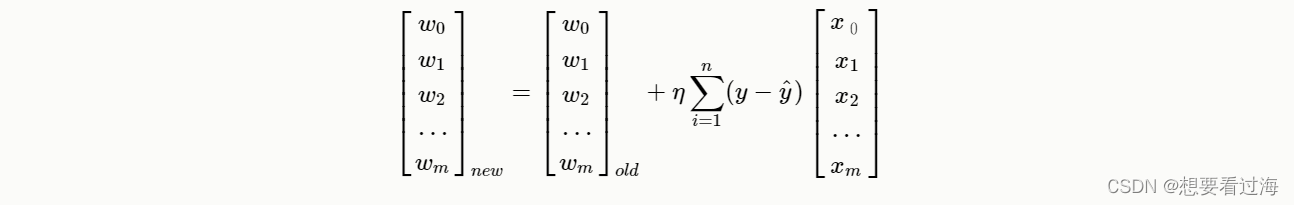
利用这种链式传播，我们就可以更新我们的每个神经元。

利用tensorFlow所实现的反向传播如下：

 logits = model(x)
                y_onehot = tf.one_hot(y, depth=10)
                # 两种计算误差函数的方法
                loss = tf.reduce_mean(tf.losses.MSE(y_onehot, logits))
                loss2 = tf.losses.categorical_crossentropy(y_onehot, logits, from_logits=True)
                loss2 = tf.reduce_mean(loss2)
                loss_meter.update_state(loss)

            # 分别对w, b求偏导
            grads = tape.gradient(loss2, model.trainable_variables)
            # 将所有参数进行原地更新。即w‘ = w - lr*grad
            optimizer.apply_gradients(zip(grads, model.trainable_variables))

五：总结

全连接网络可以经过大量数据的训练之后，对一个未知事物进行预测。是深度学习的基础。如有不足之处，还望指正。文章有所参考，但仅为少数公理。