基于Pytorch的神经网络之Regression

1.引言

我们之前已经介绍了神经网络的基本知识，神经网络的主要作用就是预测与分类，现在让我们来搭建第一个用于拟合回归的神经网络吧。

2.神经网络搭建

2.1 准备工作

要搭建拟合神经网络并绘图我们需要使用python的几个库。

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-5, 5, 100), dim=1)
y = x.pow(3) + 0.2 * torch.rand(x.size())

既然是拟合，我们当然需要一些数据啦，我选取了在区间 内的100个等间距点，并将它们排列成三次函数的图像。

2.2 搭建网络

我们定义一个类，继承了封装在torch中的一个模块，我们先分别确定输入层、隐藏层、输出层的神经元数目，继承父类后再使用torch中的.nn.Linear()函数进行输入层到隐藏层的线性变换，隐藏层也进行线性变换后传入输出层predict，接下来定义前向传播的函数forward()，使用relu()作为激活函数，最后输出predict()结果即可。

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.relu(self.hidden(x))
        return self.predict(x)

net = Net(1, 20, 1)
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()

网络的框架搭建完了，然后我们传入三层对应的神经元数目再定义优化器，这里我选取了Adam而随机梯度下降(SGD)，因为它是SGD的优化版本，效果在大部分情况下比SGD好，我们要传入这个神经网络的参数(parameters)，并定义学习率(learning rate)，学习率通常选取小于1的数，需要凭借经验并不断调试。最后我们选取均方差法(MSE)来计算损失(loss)。

2.3 训练网络

接下来我们要对我们搭建好的神经网络进行训练，我训练了2000轮(epoch)，先更新结果prediction再计算损失，接着清零梯度，然后根据loss反向传播(backward)，最后进行优化，找出最优的拟合曲线。

for t in range(2000):
    prediction = net(x)
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

3.效果

使用如下绘图的代码展示效果。

for t in range(2000):
    prediction = net(x)
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if t % 5 == 0:
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy(), s=10)
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=2)
        plt.text(2, -100, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
        plt.pause(0.1)
plt.ioff()
plt.show()

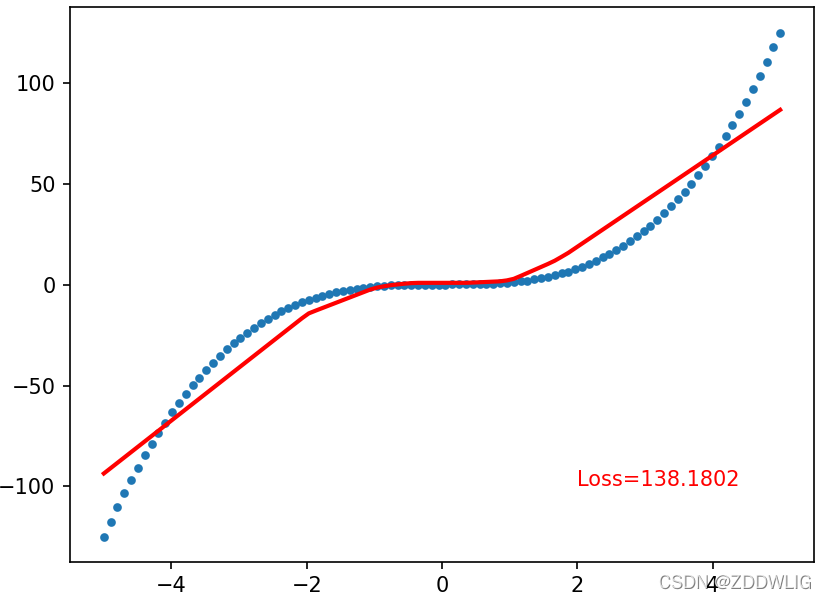
最后的结果：

4. 完整代码

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-5, 5, 100), dim=1)
y = x.pow(3) + 0.2 * torch.rand(x.size())
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.relu(self.hidden(x))
        return self.predict(x)
net = Net(1, 20, 1)
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()
plt.ion()
for t in range(2000):
    prediction = net(x)
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if t % 5 == 0:
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy(), s=10)
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=2)
        plt.text(2, -100, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
        plt.pause(0.1)
plt.ioff()
plt.show()