卡尔曼滤波介绍

一、背景介绍：

卡尔曼滤波无论是在单目标还是多目标领域都是很常用的一种算法，将卡尔曼滤波看作一种运动模型，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。

在对视频中的目标进行跟踪时，当**目标运动速度较慢**时，很容易前后两帧的目标进行关联，如下：

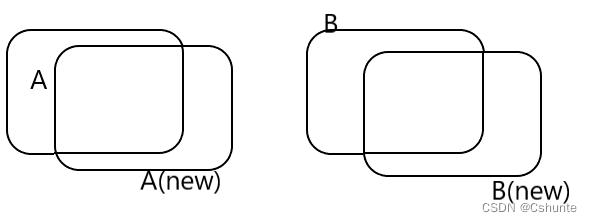
如果目标运动速度比较快，或者进行隔帧检测时，在后续帧中，目标A已运动到前一帧B所在的位置，这时再进行关联就会得到错误的结果，将A(new)和B关联在一起。

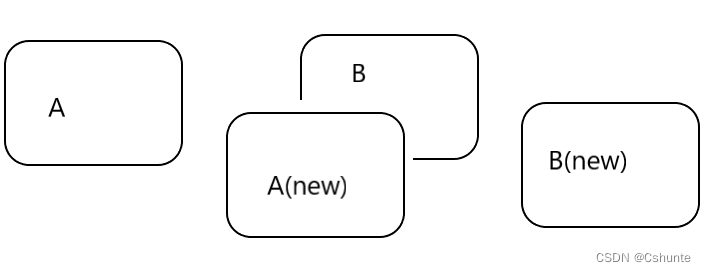
为了解决这个问题，就可以利用卡尔曼滤波，用卡尔曼滤波来预测下一帧A和B可能出现的位置，然后进行距离计算。

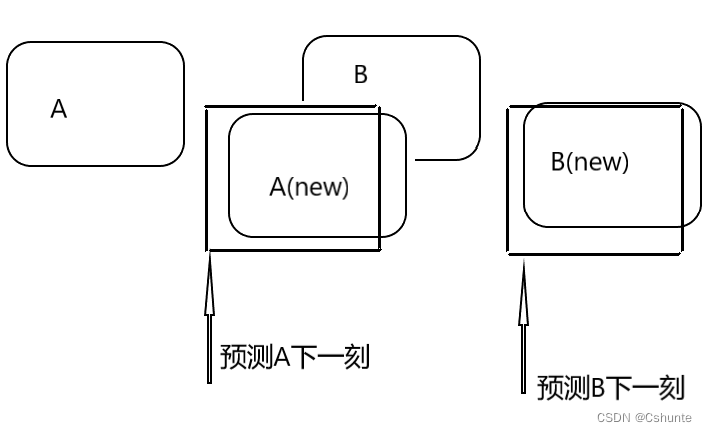
** 二、原理介绍：**

滤波器根据上一时刻（k-1时刻)的值来估计当前时刻（k时刻)的状态，得到k时刻的先验估计值;然后使 用当前时刻的测量值来更正这个估计值，得到当前时刻的估计值。

  假设有一辆小车在行使，它的速度是v，可以通过观测得到它的位置是p。（有对应的观测方程或者仪器） 

在某一时刻小车的状态可以表示为一个向量：

                                               

虽然此时小车的状态比较可信，但无论是计算还是检测都会存在一定的误差，所以我们只能认为当前状态是其真实状态的一个最优估计。

为了解释，我们不妨认为当前的状态服从高斯分布，且状态位于分布中心μ处：

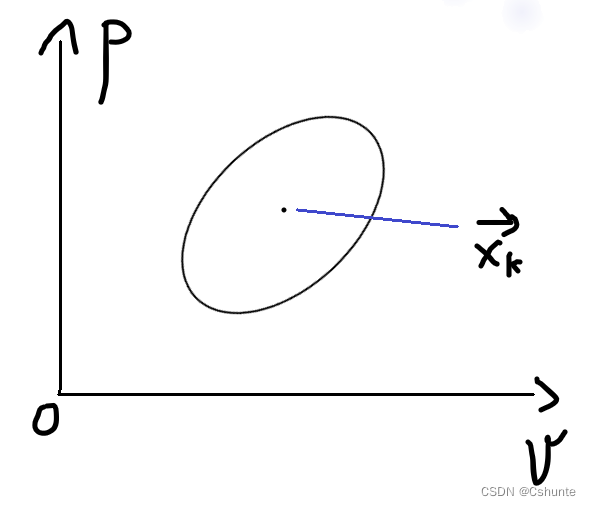
可以用一个协方差矩阵Pk来表示数据之间的相关性和离散程度：（对角线上是变量自身的方差，其余是不同变量之间的协方差）

                                             

预测下一刻的状态：

①小车做匀速运动

通过k-1时刻的位置和速度，可以预测下一个时刻的状态为：

                                            

写成矩阵的形式：                     

                                   

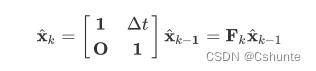
此处的Fk就是状态转移矩阵。

②小车做匀加速或者匀减速运动：

那么下一时刻的状态为：

                               

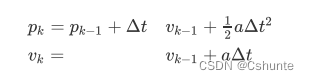
写成矩阵的形式：

                                    

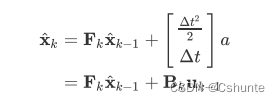
其中，Bk是状态控制矩阵，uk-1是状态控制向量。很明显，前者表明的是加速减速如何改变小车的状态，而后者则表明控制的力度大小和方向。

考虑系统的外部影响：

外界有很多影响因素能够对小车的状态产生影响，比如风速、地面摩擦等等，在这里我们假设外部的不确定因素对小车造成的系统状态误差wk服从高斯分布。于是卡尔曼滤波中完整的状态预测方程更新如下：

                                 

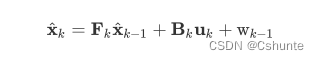
以上是预测方程的推理，下面我们来推理观测方程：

小车当前的状态和小车传感器上测量出来的结果应该具备某种特定的关系，假设这个关系通过矩阵表示为H，如下图在k时刻所示：

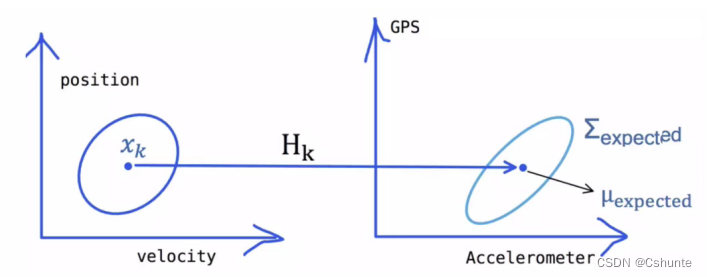
这是传感器测量出来的结果，H是一个关系矩阵，vk是传感器传来的测量噪声（大小不可测）

                                     

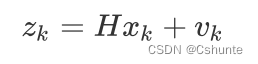
这就是卡尔曼滤波的观测方程。

于是我们从预测方程和观测方程拿到了两组Xk：

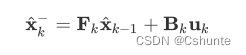
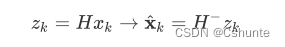
并且得到卡尔曼滤波器公式：

                                

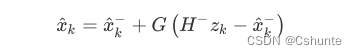
其中，G是卡尔曼增益。G=1就是完全相信观测的结果。G=0就是完全相信预测出来的结果。

我们要做的就是取一个k值，让两者加权平均出来一个相对来说方差小的结果，来作为计算出来最接近真实值的结果。

用文字来描述就是：

1.卡尔曼增益 = ( 当前估计协方差的平方 / ( 当前估计协方差的平方 + 当前测量方差的平方))

2.真实结果 = 估计值 + 卡尔曼增益 * ( 测量值 - 估计值)

三、卡尔曼滤波总结

总的来说卡尔曼滤波需要做的最重要的最核心的事就是融合预测和观测的结果，充分利用两者的不确定性来得到更加准确的估计。通俗来说就是怎么得到交集的高斯分布，看起来这是预测和观测高斯分布的重合部分，也就是概率比较高的部分。卡尔曼滤波器通过预测目标在后续帧中的位置，避免在进行目标关联时出现误差 。