谱聚类算法

1. 算法思想

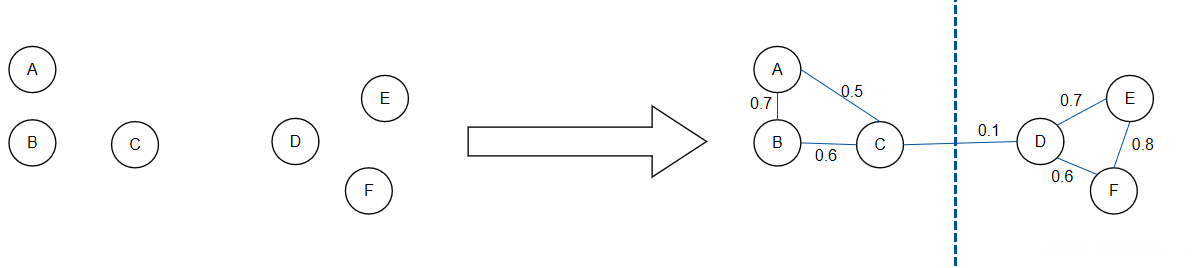
• 将所有的数据看成空间中的点，这些点之间可以用边连接起来。距离较远的点之间边的权重低，距离较近的点间边的权重高。然后对原图进行切图，使得不同子图间边的权重之和尽可能低，子图内边的权重之和尽可能高，迭代的删除最长的边，从而达到聚类的目的（如下图）。
• 简而言之，谱聚类先降维（特征分解），然后在低维空间用其它聚类算法（如KMeans、模糊聚类）进行聚类。

2. 算法流程

• 输入：样本集D=(x1,x2,…,xn)，相似矩阵的生成方式, 降维后的维度k1, 聚类方法，聚类后的维度k2
• 输出：簇划分C(c1,c2,…ck2).

（1）构建相似度矩阵（邻接矩阵）W
（2）构建度矩阵D
（3）计算拉普拉斯矩阵L、标准化后的拉普拉斯矩阵Lrm
（4）特征分解：计算Lrm最小的k1个特征值所各自对应的特征向量
（5）将各自对应的特征向量组成的矩阵按行标准化，最终组成n×k1维的特征矩阵
（6）对每一行作为一个k1维的样本，用输入的聚类方法进行聚类，聚类维数为k2。
（7）得到簇划分C(c1,c2,…ck2).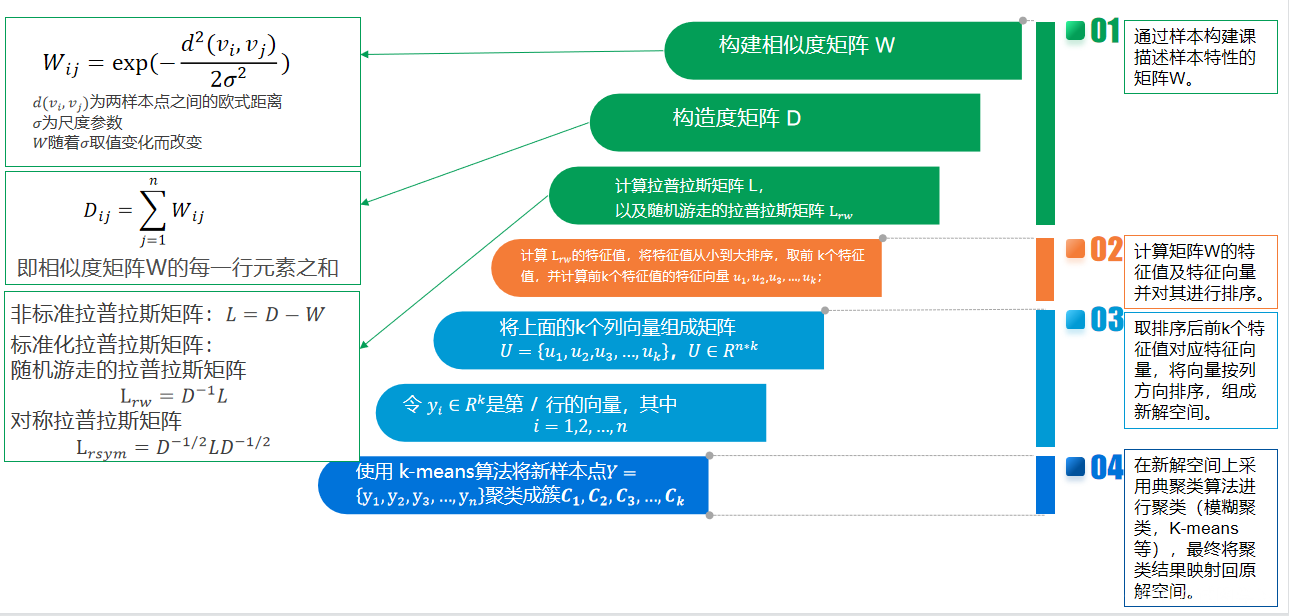　

对于输入中提及的相似矩阵的生成方式, 说明如下：
（为什么单独说名这一点，见后文缺点分析）

• 相似矩阵的生成方式 （1）ϵ-近邻法 （2）k-近邻法（本文实验所用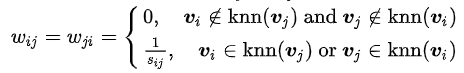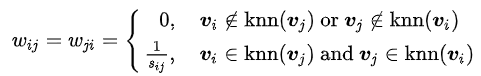） （3）全连接法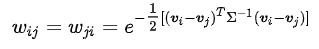

3. 实例展示

1. 数据集：ringData.mat、GaussianData.mat （以下仅展示能说明流程部分的核心代码，如需要完整版含数据集请联系作者）
2. 实现：

if __name__ =='__main__':
  cluster_num =2#聚类个数
  KNN_k =5#计算邻接矩阵W会用到
  data = loaddata()#读取数据
  W = getWbyKNN(data,KNN_k)#相似矩阵
  D = getD(W)#度矩阵
  L = D-W                     #拉普拉斯矩阵
  Lrm =(np.matrix(D))*L      #标准化拉普拉斯矩阵
  eigval,eigvec = getEigVec(L,cluster_num)#特征值、特征向量print(eigval,eigvec)
  clf = KMeans(n_clusters=cluster_num)#KMeans聚类
  s = clf.fit(eigvec)
  C = s.labels_
  centers = getCenters(data,C)#聚类中心
  plot(data,s.labels_,centers,cluster_num)

1. 聚类效果

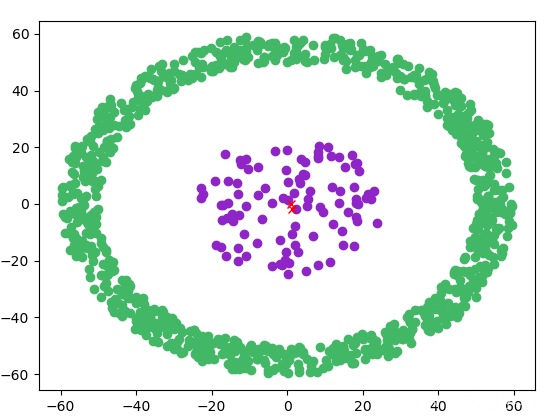
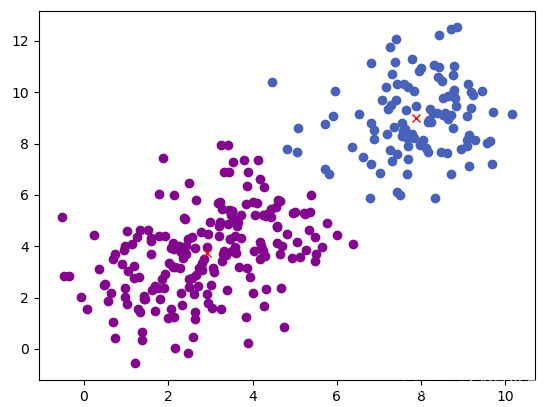
4. 优缺点

• 回忆：谱聚类可以理解为先降维，再聚类。
• 优点： （1）无需事先指定簇的数量（但如果采用kmeans进行聚类，需要指明簇的个数，正如我们下边的实例那里，手动选择簇数为2），当聚类的类别个数较小的时候，谱聚类的效果会很好； （2）谱聚类算法使用了降维的技术，所以更加适用于高维数据的聚类； （3）谱聚类只需要数据之间的相似度矩阵（邻接矩阵），因此对于处理稀疏数据的聚类很有效。 （4）与传统的聚类算法相比，它具有能在任意形状的样本空间上聚类且收敛于全局最优解
• 缺点： （1）谱聚类对相似矩阵的改变和聚类参数的选择非常的敏感； （2）谱聚类适用于均衡分类问题，对于簇之间点个数相差悬殊的聚类问题，谱聚类则不适用； （3）时间和空间复杂度大。

小结：

• 谱聚类的算法原理的确简单，代码实现比较容易。但是要完全理解，需要对图论中的无向图，线性代数和矩阵分析都有一定的了解。更多细节推导见参考。

参考：
刘建平博客园
b站白板推导
谱聚类–无需指明簇数量的聚类
sklearn谱聚类Spectral Clustering参数及算法原理
Graph特征提取方法–谱聚类
谱聚类拉普拉斯降维
深入浅出地搞懂谱聚类
谱聚类python实现
A Tutorial on Spectral Clustering
聚类算法总结
KNN和K-Means