本篇博客要分享的是使用「图神经网络」 解决「小样本」 分类问题的5个模型,每个模型都分享了单独的博客笔记,并从这些模型中总结出实现 图神经网络小样本网络 需要从哪几个方面考虑,以及后续学习路线应该如何安排。
目录
🔹 GNN
在之前学习的深度学习模型中,比如说CNN,DNN等,他们的输入都是在欧式空间定义的图片或者文字,图神经网络中的图是具有结构信息的graph,定义在非欧式空间。
Taxonomy
下图右侧是欧式空间中常见的一些神经网络的方法,比如说卷积神经网络,这种卷积的思想对应着图神经网络中的图卷积,他有两种实现的方法,分别是空间方法和谱方法。欧式空间中注意力机制的思想对应到非欧式空间就形成了图注意力网络(Graph Attention Networks),相应的还有 自编码器 对应到图自编码器( Graph Autoencoders),GAN 对应 图生成网络( Graph Generative Networks)
Structure

- 输入:原始graph
- 输出:图结点的嵌入,每个表示带有原图的特征信息。
- 学习到的特征表示被应用各种任务中
- Node-level : node clustering and classification tasks.
- Edge-level: edge classification and link prediction tasks.
- Graph-level: graph classification and generation tasks.
- Subgraph-level: subgraph classification task.
Basic GNN
下面以一个最基础的gnn来介绍一下处理步骤。
- 对于这一个简单的graph而言,输入是两个矩阵,分别是邻接矩阵和特征矩阵。
- 第一步聚合的操作是将邻接矩阵乘以特征矩阵,执行的就是对领域结点特征的一个融合操作。
- 第二步是将聚合得到的矩阵乘以参数矩阵W进行一次变换,得到新的特征矩阵。
- 最后加上当前层结点的信息,逐层向下传播,更新参数,就完成了gnn的训练。根据结点聚集和层级连接方法的不同有大量不同形式的GNN。

🔹 Few-shot:Meta-Learning
- 元学习(meta learning)是解决小样本问题非常重要的一种训练方式
- 对于一个小样本分类任务T,元学习不会直接学习如何做到这件事情,而是去学习一些相似的任务,当学习了多个这样的任务之后,元学习模型便有了举一反三的能力。(迁移学习/“学习如何学习”)。
- 比如:学会了c/c++/c# 之后,稍微看一点语法知识进行“精调”,就很容易学会 java
- 元学习具体又可以分为元训练和元测试两个阶段。
- 元训练:学习其他类似的分类任务训练模型。
- 元测试:精调元训练阶段训练好的模型,并完成小样本分类。
- 比如,我的目标小样本分类任务其实是分类长颈鹿,但是长颈鹿的样本太少了,所以在原测试阶段,模型分别学会了分类小狗,分类北极熊,分类大象,等等。然后在元测试阶段,就只需要少量的长颈鹿样本便可以完成分类了。这就是元学习的基本思想。

- 每一个小任务的训练样本为support set , 测试样本为query set。
- 元测试和元训练中所有的任务规格一致。(set大小/类别数目等)
- N-way K-shot 指元测试支持集中有N个类别,每个类别有K个样本。(下图是2-way 2-shot)
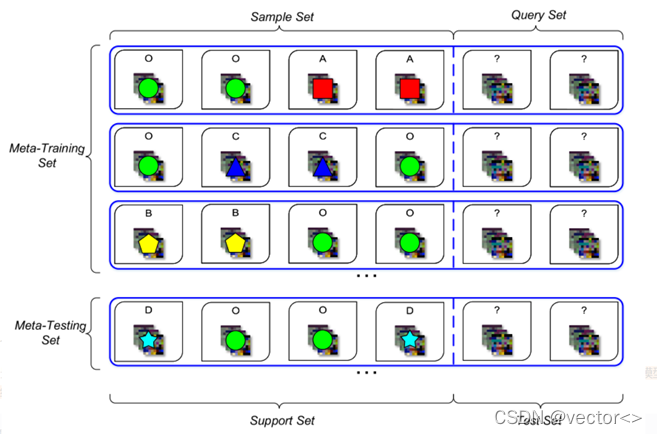
在介绍完图神经网络和元学习之后,下面要介绍的这篇文章讲的就是在图上的元学习
🔹 模型一:2019.11:Meta-GNN
- 题目:Meta-GNN: On Few-shot Node Classification in Graph Meta-learning
- 链接:https://dl.acm.org/doi/pdf/10.1145/3357384.3358106
- 笔记:【论文分享】GNN+小样本文本分类方法:Meta-GNN: On Few-shot Node Classification in Graph Meta-learning
- 源码:https://github.com/AI-DL-Conference/Meta-GNN
- 会议:CIKM (CCF-B)
- 时间:2019年11月
- 特点:GNN+元学习
动机
- 元学习作为一种模仿人类智能的可能方法最近受到了极大的关注,现有的元学习方法大多是在欧式空间中解决图像和文本等小样本学习问题。然而,将元学习应用于非欧式的研究很少,最近提出的图神经网络(GNN)模型不能有效地解决graph上的小样本学习问题。
- 本篇提出了一个针对小样本结点分类的通用图元学习框架。
方法
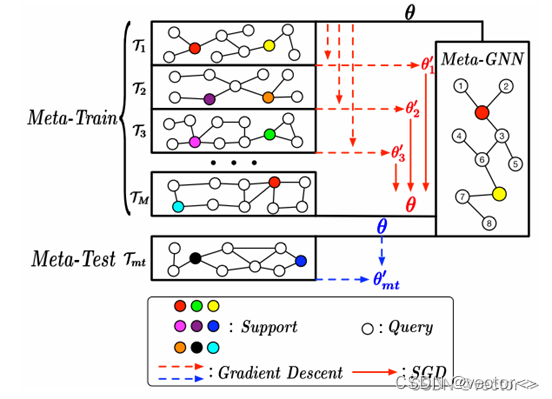
取样本
步骤:
- 从所有样本中随机抽取C2个类
- 每一个类别都随机抽取K个样本,将这K x C2 个样本构成支持集S。
- 从剩下的数据中随机抽取P个结点作为查询集Q
- 每一个任务都重复抽取支持集和查询集,共重复M次。
元训练
训练步骤:
- 对于每一个小任务,将支持集送入Meta-GNN,计算交叉熵损失。
L T i ( f θ ) = − ( ∑ x i s , y i s y i s log f θ ( x i s ) + ( 1 − y i s ) log ( 1 − f θ ( x i s ) ) ) \mathcal{L}_{\mathcal{T}_{i}}\left(f_{\boldsymbol{\theta}}\right)=-\left(\sum_{\boldsymbol{x}_{i s}, y_{i s}} y_{i s} \log f_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{i s}\right)+\left(1-y_{i s}\right) \log \left(1-f_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{i s}\right)\right)\right) LTi(fθ)=−(∑xis,yisyislogfθ(xis)+(1−yis)log(1−fθ(xis)))- 然后我们执行参数更新,在任务Ti中使用一个或几个步骤的简单梯度下降(为了简单起见,后续只描述一个梯度更新)
θ i ′ = θ − α 1 ∂ L T i ( f θ ) ∂ θ \theta_{i}^{\prime}=\theta-\alpha_{1} \frac{\partial \mathcal{L}_{\mathcal{T}_{i}}\left(f_{\theta}\right)}{\partial \boldsymbol{\theta}} θi′=θ−α1∂θ∂LTi(fθ)- α1为任务学习率,训练模型参数以优化fθ ’ 在元训练任务中的性能。更具体地说,元目标如下:
θ = arg min θ ∑ T i ∼ p ( T ) L T i ( f θ i ′ ) \boldsymbol{\theta}=\underset{\theta}{\arg \min } \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}\left(f_{\theta_{i}^{\prime}}\right) θ=θargmin∑Ti∼p(T)LTi(fθi′)- 也就是说,每个任务都使用𝜃在自己的任务上进行一次梯度更新得到 θ 𝑖 ′ \theta_𝑖^{′} θi′,最终会得到多个 θ 𝑖 ′ \theta_𝑖^{′} θi′,优化的最终目的是找一个最优的𝜃,使得每一个 θ 𝑖 ′ \theta_𝑖^{′} θi′在自身的任务上损失最小。
元测试
对于元测试,我们只需要将新的小样本学习任务支持集的节点输入到元Meta-GNN中,并通过一个或少量梯度下降步骤更新参数θ '。因此,在查询集上可以很容易地评估Meta-GNN的性能。
由于本方法是直接在graph数据集上分类,虽然将元学习引入到了graph上,但是却有很多问题没有回答,比如说:对于非graph的数据
- 结点特征如何表示?
- 边特征如何表示?
- 图如何构建?
这些问题在后面的文章中都有很好的回答。并且在后序的文章中,在得到graph之后,用元学习的方法来训练图模型,已经成为一种默认的方式。
🔹 模型二:2020.10:AwGCN
- 题目:Few-Shot Learning With Attention-Weighted Graph Convolutional Networks For Hyperspectral Image Classification
- 链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9190752
- 笔记:【论文分享】小样本图片分类方法:AwGCN:Few-Shot Learning With Attention-Weighted Graph Convolutional Networks
- 源码:-
- 会议:ICIP (CCF-C)
- 时间:2020年10月
- 特点:用CNN学习节点特征,用CNN+自注意力机制学习边特征,节点标签通过GCN传播。
介绍
分类任务:
- 对高光谱图像HSI进行小样本分类
贡献:
- 样本关系完整的图上引入GCN的半监督标签传播,现有的基于距离计算的小样本方法不同。
- 通过局部自注意机制实现注意力加权图,量化HSI小样本分类中所有样本(包括支持集和查询集)之间的关系。
方法
- 结点特征

- 边特征

- 标签传播

🔹 模型三:2020.12:EGNN-Proto
- 题目:Few-Shot Text Classification with Edge-Labeling Graph Neural Network-Based Prototypical Network
- 链接:https://aclanthology.org/2020.coling-main.485.pdf
- 笔记:【论文分享】小样本文本分类方法 EGNN-Proto:Few-Shot Text Classification with Edge-Labeling Graph Network-Based Proto
- 源码:-
- 会议:COLING (CCF-B)
- 时间:2020.12
- 特点:BERT学习文本嵌入,通过edge-labeling graph neural network改进prototypical network
介绍
动机:
- 现存的小样本文本分类方法都采用GloVe词嵌入结合CNN或RNN结构进行文本嵌入,而不是近年来提出的更高级的预训练语言模型,如ELMo 、GPT 和BERT。
- 以前的方法更多地关注文本本身的语义特征,而忽略了文本之间的潜在关系
贡献:
- 第一个将图神经网络与原型网络(prototypical network)相结合的模型
- 第一个利用EGNN (edge-labeling graph neural network) 来解决文本分类问题。
- 用Bert来学习图结点的嵌入。
这里的prototypical network 以及 EGNN 都是之前的文章提出来的比较有影响力的模型。
方法
1. Text Embedding
- 使用bert进行词嵌入
2. EGNN
- 结点特征:第一步的词嵌入
- 边特征:根据连接结点是否属于统一类初始化边缘特征,交替更新边缘特征直至收敛。
3. Prototypical network
- 没有直接通过边特征和节点特征计算查询节点的预测概率,而是引入了原型网络
- 比较所有原型向量与查询向量之间的距离,然后对查询样本进行分类

🔹 模型四:2018.02:Few-shot GNN
- 题目:Few-shot Learning With Graph Neural Networks
- 链接:https://arxiv.org/pdf/1711.04043.pdf
- 笔记:【论文分享】☆ 经典小样本GNN模型:Few-shot Learning With Graph Neural Networks【CNN+相似性度量+GCN】
- 源码:https://github.com/vgsatorras/few-shot-gnn
- 会议:ICLR
- 时间:2018.02
- 特点:这是一篇很经典的小样本+GNN文章,网上能找到的对它的阅读笔记也有很多,一度成为后续众多模型的baseline。虽然时间有点久了,但是还是有很多值得学习的地方。
方法
- 结点特征:使用CNN模型每一个图像的嵌入特征。
- 边特征:相似性度量模块学习如何将集合中的嵌入特征组成一个图。
- GNN:传播已知标签的节点特征到未知标签的节点。
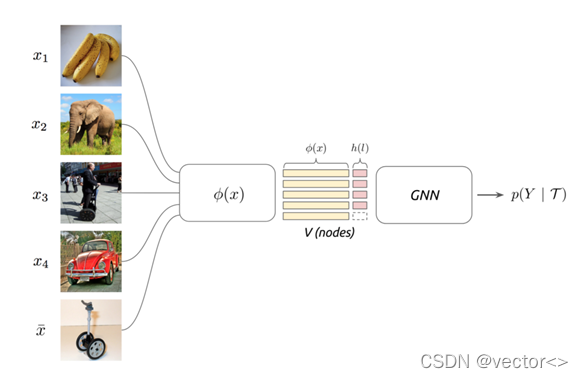
- 支持集图片与查询集图片输入到𝜙(𝑥)中。
- CNN的输出嵌入与标签的one-hot编码拼接在一起形成初始结点特征,并作为GNN的输入
可能会发现,上面提到的相似性度量模块并没有在下面这个框架图中体现,这是因为这是嵌入GNN中的一部分,是随着gnn的训练过程不断更新的,下面我们来看gnn的具体结构。

邻接矩阵定义:
- 两个向量输入到自定义的神经网络中,让网络自己学习适合GNN的度量方式。
- 得到所有节点之间的相似度之后,进而得到邻接矩阵A。
- 图神经网络每进行一次聚合与更新,都会重新计算一次相似性度量
下面来看一下相似性度量模块与神经网络的详细结构
相似性度量模块:
- 输入:结点的特征向量
- 输出:描述结点之间相似度的邻接矩阵
- 结构:若干层全连接网络

图卷积模块:
- 输入:当前层的结点的特征矩阵和邻接矩阵
- 输出:下一层的结点特征矩阵
- 结构:图卷积

🔹 小结
接下来我想对前面提到的四个模型进行一个小结。用图神经网络来处理小样本问题,对于这里的神经网络,可以从四个方面来讨论。分别是:
- 用什么方法表示结点特征?
- 用什么方法表示边的特征?
- 用什么样子的图神经网络,使用传统的GNN还是使用专门为小样本提出的GNN,这一部分的GNN指的是一些A类文章提出来的效果比较好的小样本gnn。
- 第四个是,输出层怎么处理分类问题,是直接用概率做分类,还是使用原型网络等其他方法进行分类?
- 对于小样本而言,就没有这么多花样了,当确定好模型之后,使用元学习的方法对模型进行训练和测试。

对于以上提到的四个模型,可以分别将其每个部分进行分类总结:




接下来就是最后一篇文章啦,我为什么把最后这篇文章单独拿出来讲呢?因为它是专门针对于异常检测而提出来的模型,对我更加有借鉴意义。其次时间比较新
🔹 模型五:2021.02:GDN
- 题目:Few-shot Network Anomaly Detection via Cross-network Meta-learning
- 链接:https://arxiv.org/pdf/2102.11165.pdf
- 笔记:【论文分享】★★★ 小样本网络异常检测方法 GDN:Few-shot Network Anomaly Detection via Cross-network Meta-learning
- 源码:-
- 会议:WWW(CCF-A)🔥
- 时间:2021.02
- 特点:本文提出了一种新的图神经网络系列:图偏差网络(GDN),它可以利用少量标记的异常来加强网络中异常节点和正常节点之间统计上的显著偏差;为所提出的GDN配置一种新的跨网络元学习算法,通过从多个辅助网络传输元知识来实现少镜头网络异常检测。广泛的评估证明了所提出的方法在少量或甚至一次网络异常检测的有效性。
动机
下图展示的就是这篇文章的两个点,首先提出一个图偏差网络(GDN),然后再基于GDN进行跨网络的训练,提出了Meta-GNN模型。
方法
下图的左侧是本文提出来的新的神经网络,图偏差网络GDN。右侧是对GDN进行跨网络训练得到Meta-GDN。
GDN包括以下三个关键部分:
- Network Encoder:网络编码器,用于学习节点表示。
- Abnormality Valuator:异常估值器,用于估计每个节点的异常得分。
- Deviation Loss:偏移损失,用于优化异常得分。


在前馈层的公式中:
- 𝑠_𝑖 :结点 𝑣_𝑖 的异常值;
- 𝑊_𝑠 和 𝑢_𝑠 :学习的权重矩阵和权重向量;
- 𝐛_𝑠 和 𝑏_𝑠 :偏置项。
 𝜎_𝑟是采样的r个异常分数的标准差。Yi是结点的ground-truth,也就是标准答案。我们可以一起来分析一下这个损失函数:
𝜎_𝑟是采样的r个异常分数的标准差。Yi是结点的ground-truth,也就是标准答案。我们可以一起来分析一下这个损失函数: - vi为异常节点时,yi=1,这个损失函数会使得 该异常节点的异常得分与𝜇𝑟产生至少𝑚的较大正偏差
- Vi为正常结点时,yi=0,这个损失函数会使得 正常节点的异常得分尽可能接近𝜇𝑟
- 用一句话概括一下:异常结点的异常分数,应该落在该高斯分布右侧远离均值区域 正常结点的异常值,应该落在高斯分布的均值附近。
- 这就是对异常值的一个优化

到这一步,我已经讲完了这篇文章的第一个点,也是提出了一个将graph映射为了标量异常分数的神经网络GDN,接下来我要讲的是这篇文章的第二个大的点,也就是跨网络来训练GDN。

上面这张图是本文对Meta-GDN的描述,下面这张图是今天分享的第一篇文章,Meta-GNN的描述。在我看来这两张图简直是一摸一样,总结一句话就是用元学习的策略来训练模型。可能是我的理解有错误,目前我是对这篇文章的第二个点保持怀疑态度的,因为所谓的跨网络,其实就是在网络数据集上随机抽取子图,构成元学习的支持集和查询集,进行元训练,这是在19年就有过的想法。如果后面有新的理解,我会在下一次讨论班再解释一下。
这篇文章可以归类到下图:
🔹 总结
这篇博客要分享的几个模型到这里就已经全部介绍完毕了,博主想根据这篇文章总结一下用「图神经网络」 解决「小样本」问题需要从哪几个方面考虑,以及后续学习路线应该如何安排。
对于我目前有限的了解,对小样本模型的训练和测试,一定需要使用元学习。这是目前可以明确的。那么剩下的就是要思考🍓:
- 使用什么方法表示域名的结点特征
- 使用什么方法描述域名之间的关系,也就是构建邻接矩阵,描述图的边特征。
- 使用什么样的图神经网络?是使用传统的gnn网络呢?还是使用一些A类论文中提出来的小样本图模型。对于这一步,目前我浅浅地认为,如果结点特征和边特征有比较出彩的点,其实可以使用简单一点的传统的GNN如果结点特征和边的特征方法难度不够,可以选择这些A类论文中提出来的小样本模型。目前我比较倾向的是用今天最后介绍到的GDN。
- 最后是分类层要不要用什么花样,直接用概率分类或者是使用原型网络等其他方法。
因此下一步的学习计划应该分为两大步骤🍓:
- 第一是继续去看gnn相关的小样本分类模型,看看是否有新的启发和思考。
- 第二是要学习一下,如何将域名数据构造成graph,这一部分会在后续的讨论班里面分享。

下课!
【很重要的一些话】:
由于这篇文章是博主在研究方向内的调研,前后也花了两个星期,虽然不能保证内容全部正确,但是私心是不愿意被搬运的😭,如果设置为vip文章,最低也要花98块钱才能看到,大家都是穷学生,这实在是太过分了啊!!!csdn你这里❤欠我的拿什么还啊!!所以,如果你看到了这里,说明你的研究方向和博主相似,如果这篇文章对你有一丢丢的帮助,给一个免费的一键三连吧😚😚😚
版权归原作者 vector<> 所有, 如有侵权,请联系我们删除。