栈和队列--基本操作

本节目标

**学习栈的原理及基本实现 **

学习队列的原理及基本实现

栈：

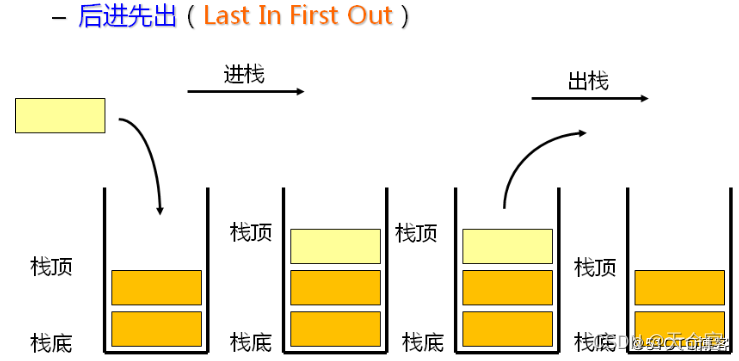
一种特殊的线性表，其只允许在固定一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵循后进先出 LIFO （Last In First Out) 的原则。

压栈：栈的插入操作叫做进栈，压栈，入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。 出数据在栈顶。

实现

1.利用顺序表实现，即使用尾插 + 尾删的方式实现

2.利用链表实现，即头尾皆可

但相对来说，顺序表的实现更为简单一点，所以优先使用栈。

public class MyStack{

   private int []array = new int [100];//建立数组大小
   private int size = 0;//

    public void push(int target){
     
        array[size++] = target;//入栈将size位置的元素置为target；
   
    }
     
     public int pop(){

    return array[--size];//出栈将size位置的元素出栈

    } 

     public int peek(){
       
       return array[size-1];
          
      }
    
     public boolean isEmpty(){

       return size = 0;
 
     }

      public int size(){

      return size;
     
      }
   }    

 

队列（Queue）

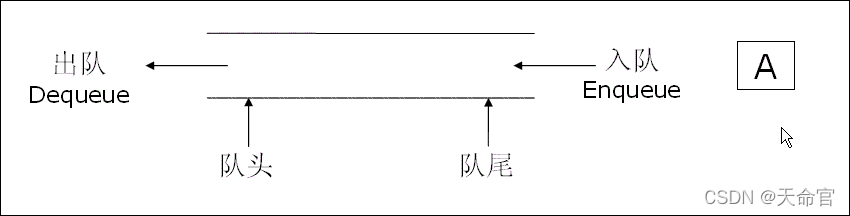
队列： 只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列；进行操作的一端称为队尾 出队列；进行删除操作的一端称为对头(Head/Front）

实现

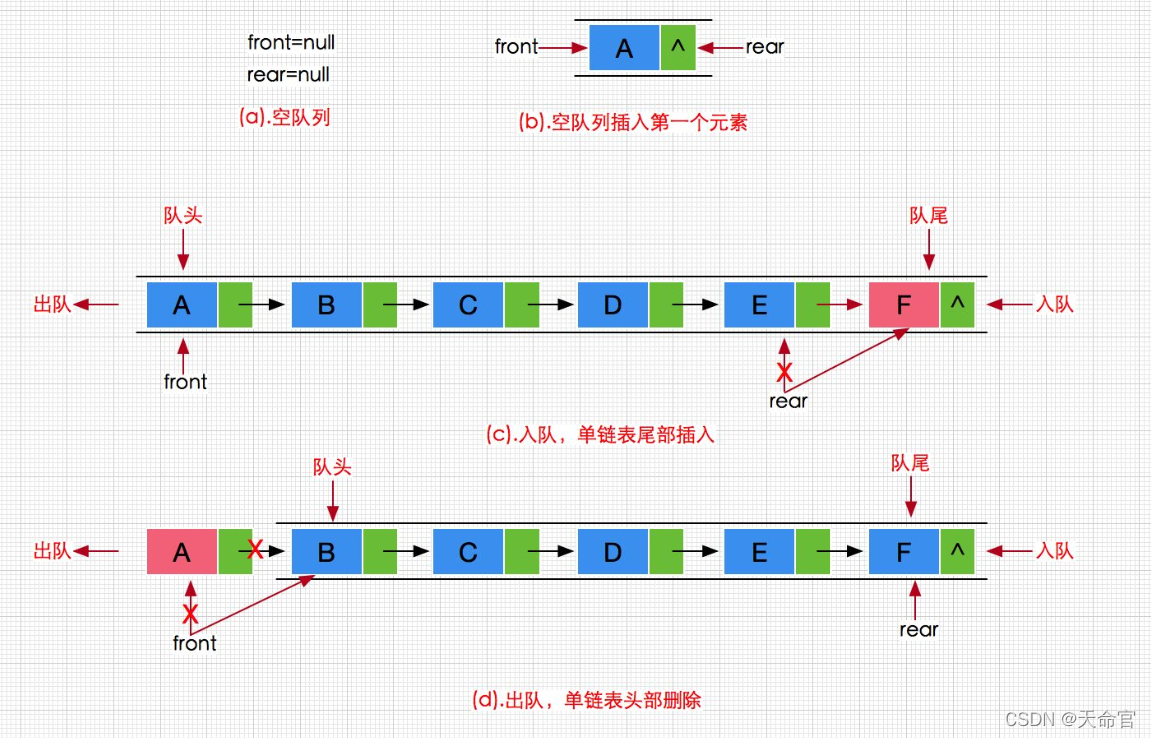
队列也可数组和链表的结构实现更有一些，因为如果使用数组结构，出栈列在数组头上出数据，效率会比较低。

    class Node{
       int val;
      Node next;

    Node(int val, Node next){

     this.val = val;
     this.next = next;
    
    }
  
    Node(int val)  {

   this(val,null);

   }
  }

      public class MyQueue{

      private Node head = null;
      private Node tail = null;
      private int size = 0;
    
    public void offer(int target){

      Node node = new Node(target);
           if(tail == null ) {
      
           head = node;
          }else{
             tail.next = node;
          }

          tail = node;
          size ++;
  
        }

      public int poll(){

       if(size == 0) {
     throw new RuntimeException("队列为空”）；
     }
   
         Node olHead = head;
         head = head.next;
        if(head == null ) {
            tail = null;
         }
            size--;
           return olHead.val;
          
           }
  
        public int peek() {
          if(size == 0 ){
              throw new  RuntimeException("队列为空”）；
          }

         public boolean  isEmoty() {

             return size == 0;
         }

         public int size() {
            
           return size ;
         }
            
      
 

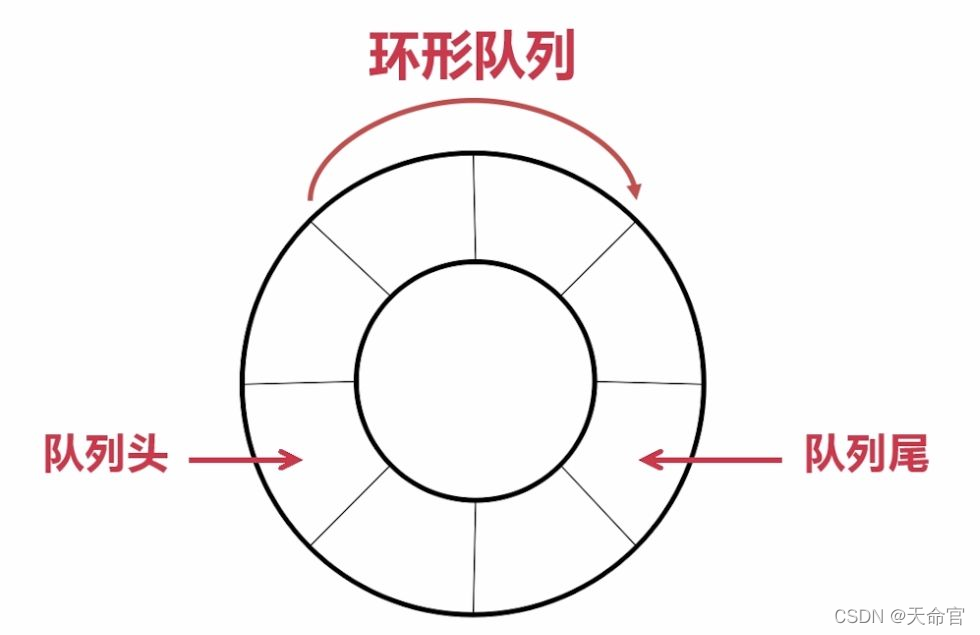
循环队列

实际上我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者模型时可以使用循环队列。环形队列通常使用数组实现。

class MyCircularQueue {
      public int[] elem;
      public int front;
      public int rear; 
    public MyCircularQueue(int k) {
     this.elem = new int[k+1];要给到一个大一个值的数组

    }
    
    public boolean enQueue(int value) {
     if( isFull()) return false;满的情况下 只能return false
     elem[rear] = value;当前尾指针放入元素
     rear = (rear+1) % elem.length;利用公式计算出下一个rear的位置
     return true;
   }
    
    public boolean deQueue() {
         if(isEmpty()) return false;空的情况下直接return false
          front = ( front+1) % elem.length;利用公式计算出front 的位置
         return true;
    }
    
    public int Front() {
       if(isEmpty()){
            return -1;
       }
       return elem[front];
    }
    
    public int Rear() {
         if(isEmpty()) return -1;
        int index = 0;
         if(rear == 0){
         index = elem.length-1;因为是 循环 所以只能是数组长度减一
         }else{
             index = rear-1; 常规操作 直接减一
         }
         return elem[index];返回
    }
    
    public boolean isEmpty() {
     return front == rear; 当front和rear 处于同一位置是 返回
    }
    public boolean isFull() {
      if((this.rear+1) % elem.length == front){这边就要用公式 rear的值只能与数组长度一致时才可
           return true;
       }
           return false;
       
}
}

下面介绍比较常用的双端队列（deque）

双端队列(deque) 指允许两端都可以进行入队和出队的操作，double ended queue。说明元素可以从对头出队和入队，也可以从队尾出队和入队。

**这一般的题目中会使用到双端队列进行解题、[Deque<> list = new LinkedList<>();] **

在解题过程中可以使用一些方法进行对队列和栈的基础操作

方法E push()压栈E pop()出栈E peek()查看栈顶元素boolean emprt()判断栈是否为空错误处理抛出异常返回特殊值入队列add(e)offer(e)出队列remove()poll()队首元素element()peek()
头部/尾部

头部元素（队首）
尾部元素错误处理抛出异常返回特殊值抛出异常返回特殊值入队列addFirst(e)offerFirst(e)addLast(e)offerLast(e)出队列removeFirst()pollFirst()removeLast()pollLast()获取元素getFirst()peekFirst()getLast()peekLast()

基本操作题

1. 括号匹配问题

2. 用队列实现栈

3. 用栈实现队列

4. 实现一个最小栈

5. 设计循环队列(在上文中介绍过）

class Solution {
    public boolean isValid(String s) {
         Stack<Character> stack = new Stack<>();创建一个栈
       for(int i = 0; i< s.length(); i++){
           char ch = s.charAt(i);循环遍历将其
           if(ch =='(' || ch == '{' || ch == '['){如果存在其中一种括号 
               stack.push(ch);放入栈中
           }else{
               if(stack.empty()){
                   return false;没有直接return false
               }
           
           char top = stack.peek();出栈顶元素
           if(top =='(' && ch == ')' || top == '{' && ch =='}' || top == '[' && ch == ']'){ 当top 值与 ch 值相同时  出
           stack.pop();

         }else{不相同 return false
           return false;
       }
       }
    }
    if(!stack.empty()){ 最后判断 栈中还有元素 说明匹配的括号多 无法全部配对成功
        return false; 
    }
    return true;
}
}

class MyStack {
    private Queue<Integer> pu1;
    private Queue<Integer> pu2;
    public MyStack() {
  pu1 = new LinkedList<>();
  pu2 = new LinkedList<>();

    }
    
    public void push(int x) {
     if(!pu1.isEmpty()){队列1 不为空 直接放入
         pu1.offer(x);
     }else if(!pu2.isEmpty()){队列2 不为空 直接放入
         pu2.offer(x);
     }else{
     pu1.offer(x);
    }
    }
    
    public int pop() {
        if(!pu1.isEmpty()){队列1 不为空
            int size = pu1.size()-1;
            for(int i = 0; i< size; i++){
              pu2.offer(pu1.poll()); 将队列1 中元素挨个放进 队列2 中
            }
           return  pu1.poll();
          
           
        }
              if(!pu2.isEmpty()){队列2 不为空
            int size = pu2.size()-1;
            for(int i = 0; i< size; i++){ 循环为 队列2 长度-1
              pu1.offer(pu2.poll()); 将其放入队列1 中
            }
            return   pu2.poll();
            
        }
        return-1;
    }

         
   
    public int top() {
       if(empty()) return -1;
      if(!pu1.isEmpty()){
          int val = -1;
             int size =  pu1.size();
            for(int i = 0; i<size; i++){将队列1中元素放入2中
                 val =  pu1.poll();
             pu2.offer(   val); 
         }
         return val;
    }
     if(!pu2.isEmpty()){
         int val = -1;
            int size = pu2.size();
            for(int i = 0; i<size; i++){将队列2中放入1中
             val =    pu2.poll() ;
             pu1.offer( val);
         }
         return val;
     }
     return -1;
    }
    public boolean empty() {
  return pu1.isEmpty() && pu2.isEmpty();
    }
}

class MyQueue {
        public Stack<Integer> stack1;
    public Stack<Integer> stack2;
    public MyQueue() {
       stack1 = new Stack<>();
     stack2 = new Stack<>();
    }
    
    public void push(int x) {
      stack1.push(x);直接放入元素

    }
    
    public int pop() {
          if(empty()) return -1;
          if(stack2.empty()){
          while(!stack1.isEmpty()){栈2不为空栈1为空的情况下
              stack2.push(stack1.pop());将栈1中元素放入2中
          }
        
    }
      return stack2.pop();
    } 
    public int peek() {
   if(empty()) return -1;
          if(stack2.empty()){栈1不为空栈2为空的情况下
          while(!stack1.isEmpty()){
              stack2.push(stack1.pop());将栈1中元素放入2中
          }
            
    }
     return stack2.peek();
    } 
    
    public boolean empty() {
   return stack1.isEmpty() && stack2.isEmpty();
    }
}

class MinStack {

   private Stack<Integer> stack;
   private Stack<Integer> minstack;
   
   
    public MinStack() {建立两个栈进行存放
       stack = new Stack< >();
       minstack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(!minstack.empty()){
            int top = minstack.peek();最小栈不为空的情况下 
            if(  val <= top  ){将给出的值与最小栈的栈顶元素进行比较 
                minstack.push(val);小则将其放入
            }
        }else{
            minstack.push(val);

        }

    }
    
    public void pop() {
        int pro = stack.pop();
        if(!minstack.empty()){
           int tmp =  minstack.peek();
            if( tmp == pro ){这是在其相同的情况下
                minstack.pop();最小栈要出元素
            }
        }
    }
    
    public int top() {
  return stack.peek();
    }
    
    public int getMin() {
  return minstack.peek();获取最小元素直接将最下栈的栈顶元素返回
    }
}

本文中所出现的题目全来自力扣原题 ！！！

由于初次接触博客希望各位前辈给出宝贵的意见 谢谢！！！