神经网络案例编程实战

一、数据预处理

   在训练神经网络前一般需要对数据进行预处理，一种重要的预处理手段就是归一化处理。下面简单介绍一下归一化处理的原理和方法。

（1）什么是归一化？

数据归一化就是把数据同等降低维度，比如说一组数据是[99，98，97，100]，那么为了更好的效果，我们可以把这组数据归一化处理得到[0.99,0.98,0.97,1].

（2）为什么要归一化处理？

     a.输入数据的单位不一样，归一化处理后得到一个统一的单位

     b.有些数据的范围可能会特别大，导致的结果是神经网络收敛慢，从而导致训练时间变长

（3）归一化算法

一种简单而快速的归一化算法是线性转换算法。线性转换算法常见的有两种形式：

    1. Y=(X-min)/(max-min)：其中min为x的最小值，max为x的最大值，输入向量为x，归一化后的输出向量为y。上式将数据归一化到[0,1]区间，当激活函数采用S形函数时（值域为(0,1)）时这条式子适用。

    2.y=2*（x-min)/(max-min)-1：这条公式将数据归一化到[-1,1]区间，当激活函数采用双极S形函数(值域为(-1,1))时这条式子适用。

二、BP神经网络的训练过程

（1）初始化网络的突触权值和阈值矩阵；

（2）训练样本的呈现；

（3）前向传播计算；

（4）误差方向传播计算并更新权值；

（5）迭代，用新的样本进行步骤3和4，直至满足停止准则。

三、BP神经网络的测试过程

（1）数据分为训练数据和测试数据，根据训练数据训练模型，再根据测试数据验证模型训练的正确性质。

（2）将测试数据输入模型，得到理论测试输出和实际输出，对比后即可确定模型预测的正确率

基础代码：

%这个只能做已知条件内的预测
%BP网络函数逼近实例
%1.首先定义正弦函数，采样率为20Hz，频率为1Hz
k=1;%设定正弦信频率 
p=[0:0.05:40]; 
t=cos(k*pi*p)+3*sin(k*pi*p);
%figure(1); 
%plot(p,t,'-'); 
%xlabel('时间');
%ylabel('输入信号');
%title('正确信号’); 
% 2.生成BP网络。用newff函数生成前向型BP网络，设定隐层中神经元数目为10 
%分别选择隐层的传递函数为tansig，输出层的传递函数为purelin， 
%学习算法为trainlm。 
net=newff(minmax(p),[10,10,1],{'tansig','tansig','purelin'},'trainlm');
%对生成的网络进行仿真并做图显示。 
%y1= sim(net,p);plot(p，t,'-',p,y1,'__') 
%4.训练。对网络进行训练，设定训练误差目标为 1e-5，最大迭代次数为300. 
%学习速率为0.05. 
net.trainParam.lr=0.05;
net.trainParam.epochs=10000;
net.trainParam.goal=1e-5; 
[net,tr]=train(net,p,t); 
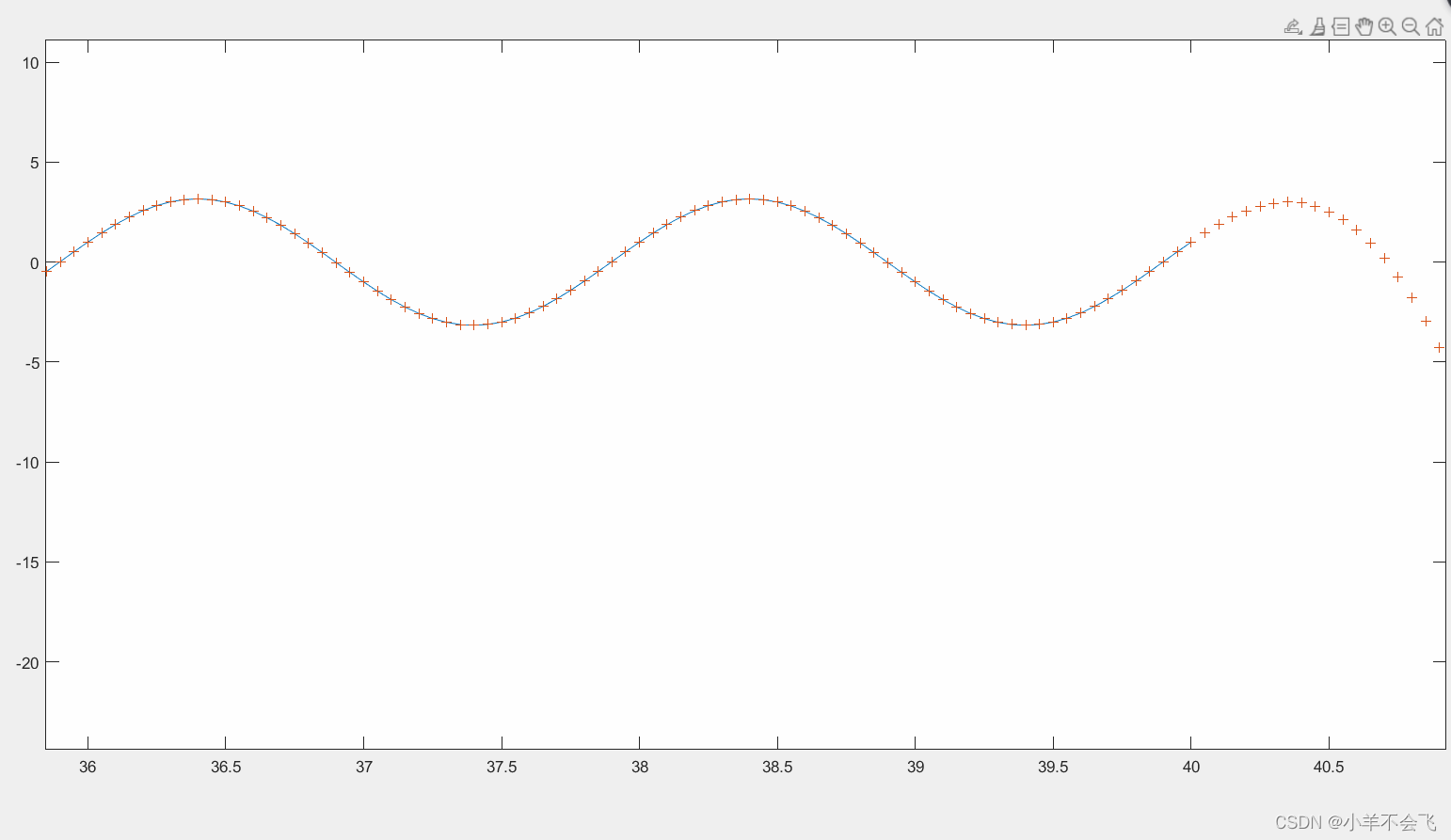
%5.再次对生成的网络进行仿真并做图显示。 
y2=sim(net,p); 
plot(p,t,'-',p,y2,'+') 

使用Matlab建立前馈神经网络主要会使用到下面3个函数：

newff：前馈网络创建函数

train：训练一个神经网络

sim：使用网络进行仿真

（3）newff函数语法

newff函数参数列表有很多的可选参数，这里介绍newff函数的一种简单的形式。

语法：net=newff（A,B,{C},'trainFun'）

参数解释：

A：一个n*2的矩阵，第i行元素为输入信号xi的最小值和最大值；

B：一个k维行向量，其元素为网络中各层节点数；

C:一个k维字符串行向量，每一分量为对应层神经元的激活函数；

trainFun：为学习规则采用的训练算法。

（4）常用的激活函数

1.线性函数：'purelin'

2.对数S形转移函数：'logsig'

3.双曲正切S形函数：'tansig'

（5）常见的训练函数

1.traingd：梯度下降BP训练函数

2.traingdx：梯度下降自适应学习率训练函数

（6）网络配置参数

net.trainparam.goal：神经网络训练的目标误差

net.trainparam.show：显示中间结果的周期

net.trainparam.epochs：最大迭代次数

net.trainparam..lr：学习率

（7）train函数（网络训练学习函数）

语法:[net,tr]=train(net,X,Y)

参数：

X：网络实际输入

Y：网络应有输出

tr：训练跟踪信息

Y1：网络实际输出

E：误差矩阵

（8）sim函数

语法：Y=sim(net,X)

参数：

net:网络

X：输入给网络的K*N矩阵，其中K为网络输入个数，N为数据样本数

Y：输出矩阵Q*N，其中Q为网络输出个数

总结：

本次经过实战测试，发现该代码用来做已知数据范围内的预测效果比较好【比如在X为[0，5000]范围进行训练，然后预测X=4000时候的情况是比较好的，预测X>5000时，效果不佳】，预测未知数据建议使用灰色预测或其他预测方法