【人工智能】消解反演复习

CH4：谓词逻辑表示与推理技术

需要了解有关离散数学的基础概念

谓词逻辑法

谓词逻辑法采用谓词合式公式和一阶谓词演算把要解决的问题变为一个有待证明的问题,然后采用消解原理和消解反演来证明一个新语句是从已知的正确语句导出的, 从而证明新语句也是正确的.

命题逻辑虽能够把客观世界的各种实事表示为逻辑命题，但具有很大局限性，即不适合表达比较复杂的问题；而谓词逻辑则允许我们表达那些无法用命题逻辑表达的事情。

置换(Subtitution)&合一(Unification)

置换（Subtitution)是形如： { t1/x1，t2/x2，…， tn/xn}的有限集合。其中，ti是不同于xi的项（常量、变量、函数）；x1，x2， …，xn必须是互不相同的变量； ti/xi 表示用ti代换xi。

• 令置换 s＝{t1/x1, … ,tn/xn}，而E是一谓词公式， 那么s作用于E，就是将E中出现的变量xi均以ti代入(i=1, … ,n),结果以Es表示，并称为E的一个例。
• 置换乘法（合成）： 若 θ ＝ { t 1 / x 1 , … , t n / x n } , λ ＝ { u 1 / y 1 , … , u m / y m } 置换的乘积 θ ⋅ λ : 1. 先作置换 : { t 1 ⋅ λ / x 1 , … , t n ⋅ λ / x n , u 1 / y 1 , … , u m / y m } 2. 若 y i ∈ { x 1 , … , x n } 时，先从中删除 u i / y i ; 3. t i ⋅ λ = x i 时，再从中删除 t i ⋅ λ / x i 所得的置换称作 θ 与 λ 的乘积，记作 θ ⋅ λ 若 θ＝{t_1/x_1,…,t_n/x_n},λ＝{u_1/y_1,…,u_m/y_m}\ 置换的乘积θ·λ:\ 1.先作置换:{t_1·λ/x_1,…,t_n·λ/x_n,u_1/y_1,… ,u_m/y_m}\ 2.若yi∈{x_1,…,x_n}时，先从中删除u_i/y_i;\ 3.t_i·λ=x_i 时，再从中删除t_i·λ/x_i\ 所得的置换称作θ与λ的乘积，记作θ·λ 若θ＝{t1​/x1​,…,tn​/xn​},λ＝{u1​/y1​,…,um​/ym​}置换的乘积θ⋅λ:1.先作置换:{t1​⋅λ/x1​,…,tn​⋅λ/xn​,u1​/y1​,…,um​/ym​}2.若yi∈{x1​,…,xn​}时，先从中删除ui​/yi​;3.ti​⋅λ=xi​时，再从中删除ti​⋅λ/xi​所得的置换称作θ与λ的乘积，记作θ⋅λ 一个例子：
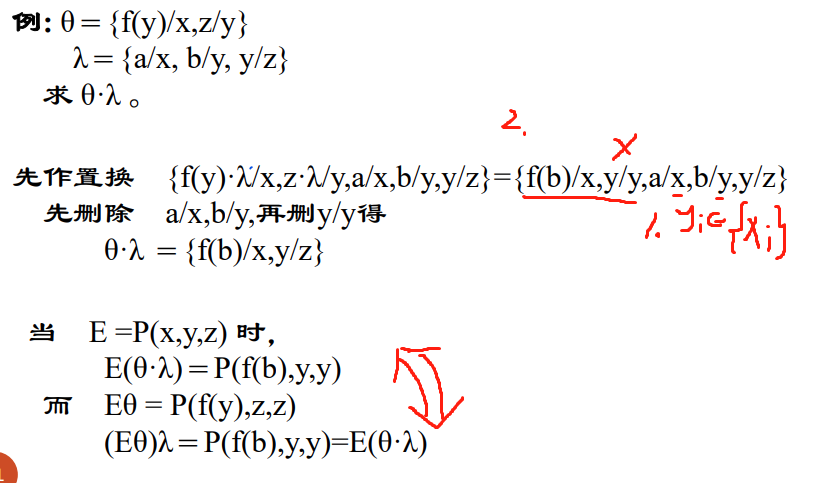
• 置换可结合：- s1s2表示两个置换s1和s2的合成，L表示一表达式，则有：(LS1)S2=L(S1S2)，(S1S2)S3=S1(S2S3)；- 一般地，置换不可交换。

合一：寻找项对变量的置换，以使两表达式一致。

一个置换s作用于表达式集{Ei}的每个元素,则我们用**{Ei}s**来表示置换例的集。

• {Ei}是可合一的：如果存在一个置换s， 使得E1s= E2s= E3s=…。此s为{Ei}的合一者。
• 最一般合一者（记为mgu）：通过置换最少的变量以使表达式一致。

例：表达式集 {P[x, f(y), B], P[x, f(B), B]} 的合一者为 s={A/x, B/y}, s使表达式成为单一形式 P[A,f(B), B];

​ 最简单的合一者应为: g={B/y}

消解原理

又称为归结原理。是一种基于逻辑的、采用反证法的推理方法，是机器定理证明的主要方法。

消解法的基本原理：采用反证法或者称为反演推理方法，将待证明的表达式（定理）转换成为逻辑公式（谓词公式），然后再进行归结，归结能够顺利完成，则证明原公式(定理）是正确的。

证明的基本思想：

• 设F1、 … 、Fn、G为公式，G为F1、 … 、Fn的逻辑推论，当 且仅当公式（（F1∧…∧Fn）→ G）是有效的。
• 反证法：设F1、 … 、Fn、G为公式，G为F1、…、Fn的逻辑推论，当且仅当公式（F1∧…∧Fn ∧ ¬G）是不可满足的。

一些概念：

• 文字：一个原子公式和原子公式的否定都叫做文字，如：P(x)，¬P(x,f(x))，Q(x, g(x))
• 子句：由文字的析取组成的公式，如： P(x)∨Q(x), ¬P(x,f(x))∨Q(x,g(x))
• 空子句：不包含任何文字的子句
• 子句集：由子句构成的集合
• 消解：消解过程被应用于母体子句对，以便产生一个导出子句例如，如果存在某个公理E1∨E2和另一公理 E2∨E3，那么E1∨E3在逻辑上成立，这就是消解。而称E1∨E3为E1∨E2和E2∨E3的消解式（resolvent）

任何谓词公式F都可通过等价关系及推理规则化为相应的子句集S

子句集的求取：

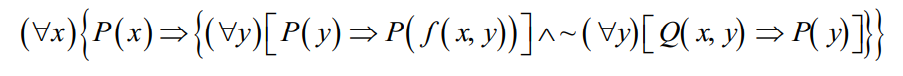
1. 消去蕴涵符号：只应用∨和~符号，例如以 ¬A∨B替换A→B。
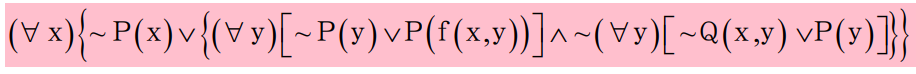
2. 减少否定符号的辖域：每个否定符号最多只用到一个谓词符号上，并反复应用狄·摩根定律。如：- 以A∨B代替 (A∧B)，- 以A∧B代替~(A∨B)，- 以(∃x){A}代替(∀x)A，- 以(∀x){A}代替(∃x)A，- 以A代替(A）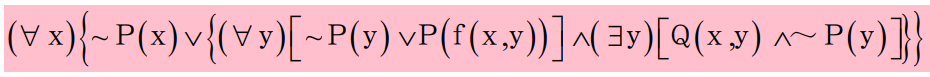
3. 对变量标准化（“换名”）：对哑元（受量词约束的变量）改名以保证每个量词有其自己唯一的哑元。
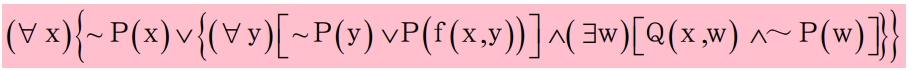
4. 消去存在量词：1. 如果要消去的存在量词在某些全称量词的辖域内：如(∀y) [ (∃x) P(x,y) ] ——> (∀y)P(g( y), y)- 以一个Skolem函数代替每个出现的存在量词的量化变量，这里就是用Skolem函数代替∃的量化变量x。- Skolem函数的变量就是全称量词所约束的全称量词量化变量，所以Skolem函数的变量就是∀约束的y。- Skolem函数所使用的函数符号必须是新的，即不允许是公式中已经出现过的函数符号。2. 如果要消去的存在量词不在任何一个全称量词的辖域内，那么就使用不含变量的Skolem函数即常量。例如：(∃x)P(x)化为P(A)。常量符号A用来表示我们知道的存在实体。A必须是个新的常量符号，即未曾在公式中其它地方使用过。
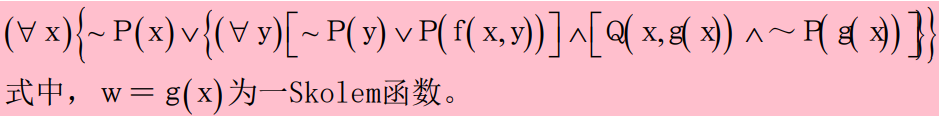
5. 化为前束形：把所有全称量词移到公式的左边，并使每个量词的辖域包括这个量词后面公式的整个部分。前束形 = (前缀) (母式)​ = （全称量词串） （无量词公式）
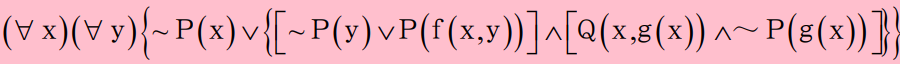
6. 把母式化为合取范式（由一些谓词公式和(或)谓词公式的否定的析取的有限集组成的合取。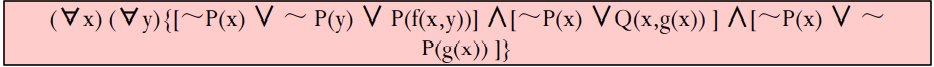）> 这里用了分配律
7. 消去全称量词
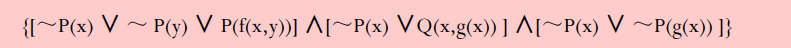
8. 消去连词符号∧：用 { (A∨B) , (A∨C) } 代替(A∨B)∧(A∨C)最后得到一个有限集， 其中每个公式是文字的析取。任一个只由文字的析取构成的合式公式叫做一个子句。
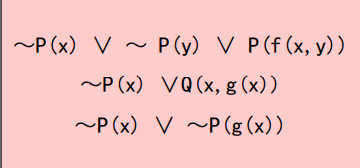
9. 更换变量名称：例如{P(x)∨P(y)∨P[f(x,y)], ~P(x)∨Q[x,g(x)], P(x)∨P[g(x)]}，使一个变量符号不出现在一个以上的子句中：- ~P(x) ∨ ~P(y) ∨ P[f(x, y)] ——> ~P(x1) ∨ ~P(y) ∨ P[f(x1, y)]- ~P(x) ∨ Q[x, g(x)] ——> ~P(x2) ∨ Q[x2, g(x2)]- ~P(x) ∨ ~P[g(x)]} ——> ~P(x3) ∨ ~P[g(x3)]

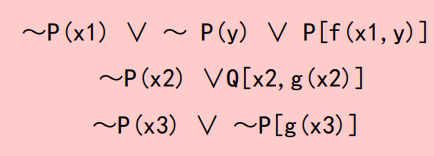
消解反演

应用归结原理证明定理的过程称为归结（消解）反演。

一般过程：

1. 建立子句集S
2. 从子句集S出发,对S的子句使用归结推理规则
3. 如果得出空子句, 则结束;否则转下一步
4. 将所得归结式仍放入S中
5. 对新的子句集使用归结推理规则
6. 转3

说明两点：

• 空子句不含有文字,它不能被任何解释满足, 所以空子句是永假的,不可满足的。
• 归结过程出现空子句,说明出现互补文字,说明S中有矛盾,因此S是不可满足的。

如欲证明Q为P1 ,P2 ,…,Pn的逻辑结论，只需证(P1∧P2∧…∧Pn)∧¬Q是不可满足的。

F为已知前提的公式集，Q为目标公式(结论)，用归结反演进行证明的步骤是：

1. 否定Q，得到¬Q；
2. 把¬Q并入到公式集F中，得到{F, ¬Q};
3. 把公式集{F, ¬Q}化为子句集S；
4. 应用消解推理规则对子句集S中的子句进行归结，并把每次归结得到的归结式都并入S中。如此反复进行，若出现了空子句，则停止归结。

消解推理规则

消解的定义：

​ 令L1，L2为两任意原子公式：L1和L2具有相同的谓词符号，但一般具有不同的变量，已知两个子句L1∨ α 和～L2 ∨ β，如果L1和L2具有最一般合一σ，那么通过消解可以从两个父辈子句推导出一个新子句（α∨β）σ。这个新子句叫做消解式。

消解式求法：

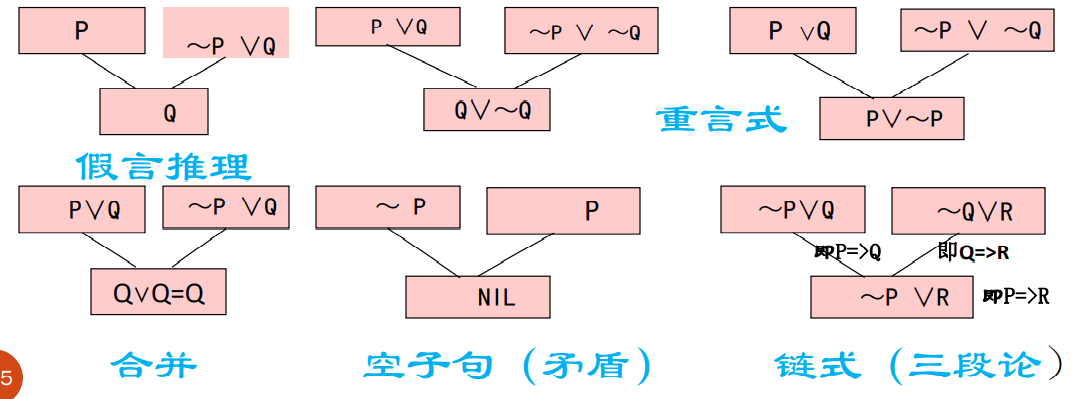
含有变量的消解式

必须找到一个作用于父辈子句的置换，使父辈子句含有互补文字：

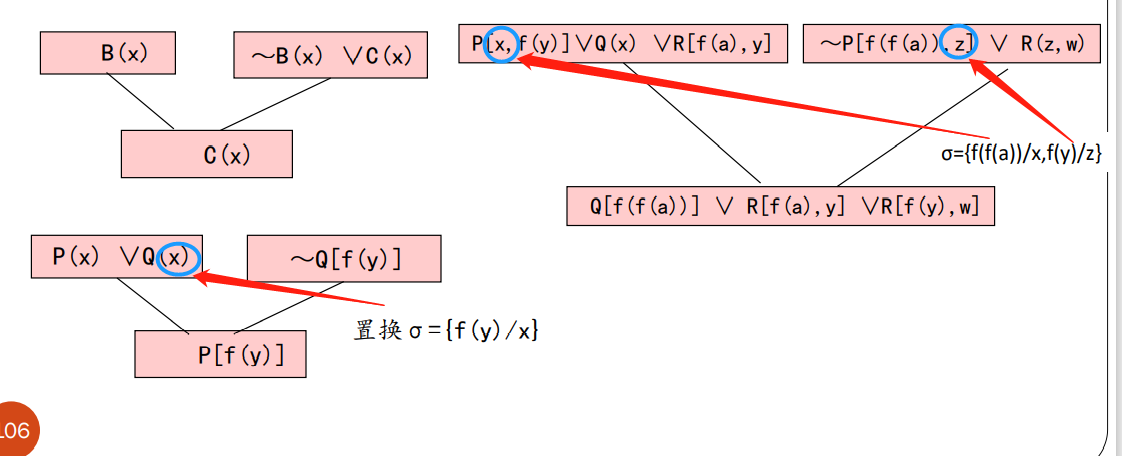
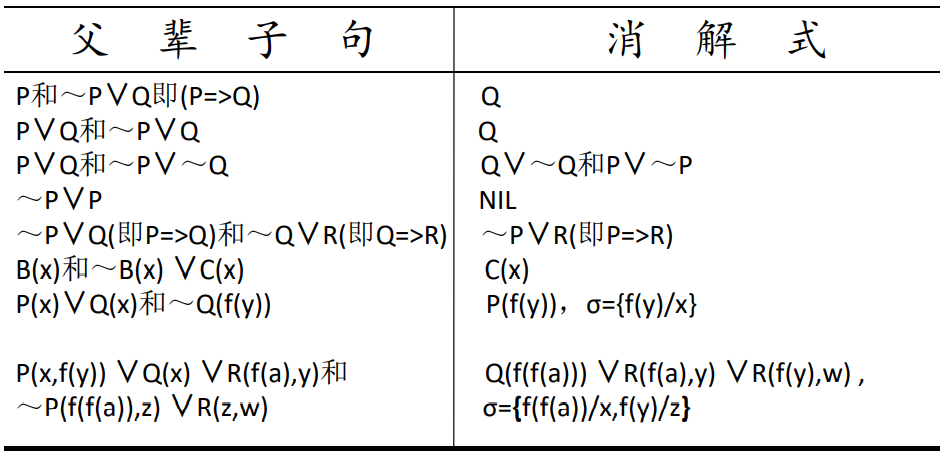
消解推理的常用规则

反演求解过程

例：“如果无论约翰(John)到哪里去，菲多(Fido)也就去那里，那么如果约翰在学校里，菲多在哪里呢?”

• 公式集S：(∀x) [AT(JOHN, x) ⇒ AT(FIDO, x)]，AT(JOHN,SCHOOL)
• 把问题化为一个包含某个存在量词的目标公式，使得此存在量词量化变量表示对该问题的一个解答：**(∃x)AT(FIDO,x)**

（1）把由目标公式的否定产生的每个子句添加到目标公式否定之否定的子句中去。

目标公式的否定产生：**(∀x)[～AT(FIDO,x)]，其子句形式为：～AT(FIDO,x)**，把它添加至目标公式的否定之否定的子句中去，得重言式：～AT(FIDO,x)∨AT(FIDO,x）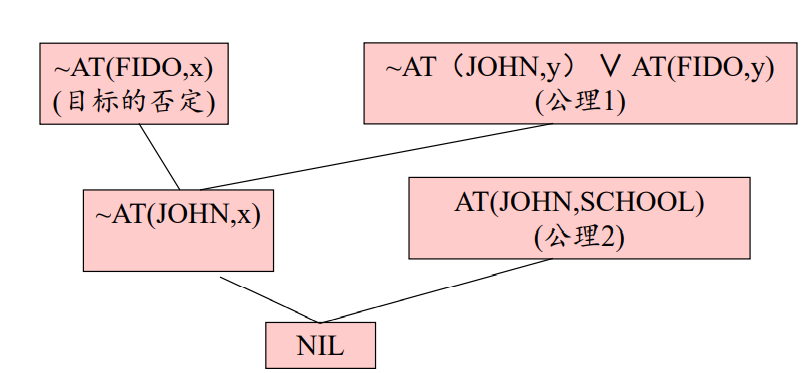

（2）按照反演树，执行和以前相同的消解，直至在根部得到某个子句为止。

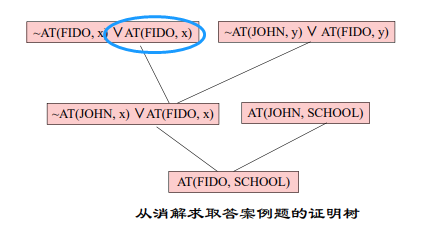
（3）用根部的子句作为一个回答语句。子句AT (FIDO，SCHOOL)就是这个问题的合适答案。

变换关系涉及到把由目标公式的否定产生的每个子句变换为一个重言式

把一棵根部有NIL的反演树变换为根部带有回答语句的一棵证明树

注意：在消解之前仍然要严格遵循子句集求解的步骤！比如（1）中的变量名已经被替换为不同的x和y

语义网络法

语义网络是知识的一种结构化图解表示，它由节点和弧线组成。

节点用于表示实体、概念和情况等，节点之间的弧线用于表示节点间的关系。

二元语义网络

1. 表示简单的事实：
2. 表示占有关系和其它情况：
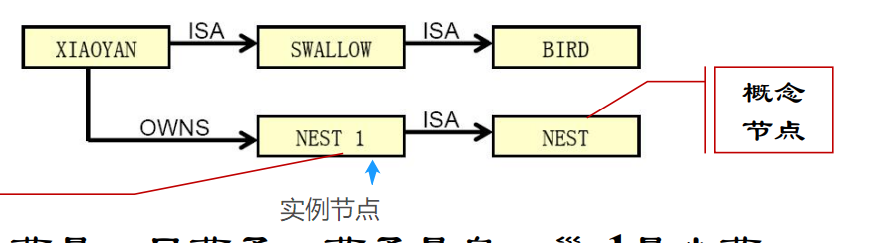
3. 用一组基元来表示知识：

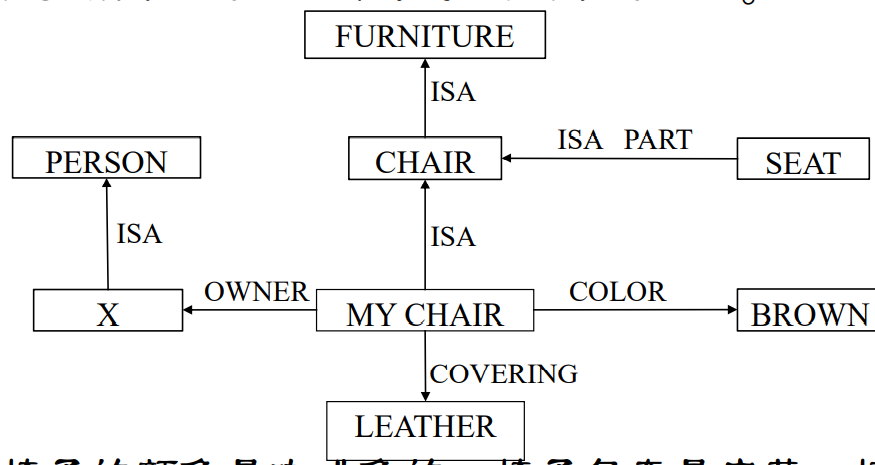
多元语义网络

多元关系可转化成一组二元关系的组合，或二元关系的合取。

表示

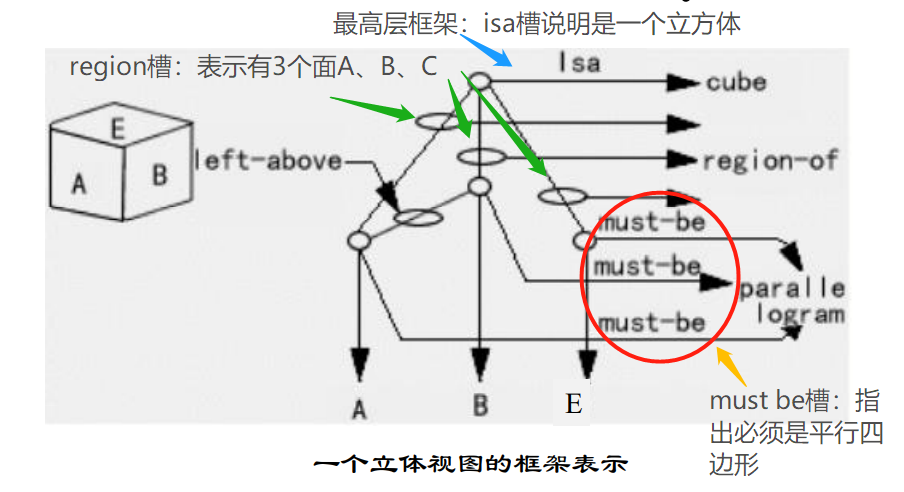
框架表示

是一种结构化表示法，通常采用语 义网络中的节点-槽-值表示结构。

特征：

• 有一个框架名（可带有参数）
• 有一组属性，每个属性称为一个槽，里面可存放属性值。 - 每个属性对值有要求，不同属性的类型可不同- 有些属性值可为子框架调用（可带参数）- 有些属性值是预先确定，有些属性值需在生成实例时代入- 有些属性值在代入时需满足一定条件，有时，在不同属性的属性值之间还有一些条件需要满足

剧本表示

框架的一种特殊形式，它用一组槽来描述某些事件 的发生序列。

构成：

• 开场条件：给出在剧本中描述的事件发生的前提条件。
• 角色：用来表示在剧本所描述的事件中可能出现的有关人物的一些槽。
• 道具：这是用来表示在剧本所描述的事件中可能出现的有关物体的一些槽。
• 场景：描述事件发生的真实顺序，可以由多个场景组成，每个场景又可以是其它的剧本。
• 结果：给出在剧本所描述的事件发生以后通常所产生的结果。

与框架相比：要呆板得多，知识表达的范围也很窄，因此不适用于表达各种知识，但对于表达预先构思好的特定知识，如理解故事情节等，是非常有效的。

剧本的两个特点：

1. 一旦剧本被启用，则可以应用它来进行推理。其中最重要的是运用剧本可以预测没有明显提及的事件的发生。
2. 一个典型的事件被中断，也就是给定情节中的某个事件与剧本中的事件不能对应时，则剧本便不能预测被中断以后的事件了。