搞清楚这些问题，你将吃透二叉搜索树的基础内容

搞清楚这些问题，你将吃透二叉搜索树的基础内容

前言

本文主要以简单明了的大白话讲解有关二叉搜索树中一些比较常规的重要知识以及一些常考的重要操作，不限于二叉搜索树的基本定义，二叉搜索树中的如何进行查找删除和插入

注意：在学习本文的过程中，先确保自己没有三高等疾病（敲重点：因为在阅读的过程中你会发现你会经历一个 情绪跌宕起伏 的过程，曲线类似 正态分布 , 非常刺激 ），否则出现任何严重后果本博主概不负责，让你深度理解二叉搜索树中的这些重要的操作

目录

1、什么是二叉搜索树?

2、如何轻松愉快地理解二叉搜索树中查找操作?

3、如何闭着眼睛将二叉搜索树中的非递归删除操作清楚地浮现在脑海里?

4、在二叉搜索树的插入操作中那些你应该注意的事情?

正文

1、什么是二叉搜索树？

二叉搜索树：顾名思义，就是一棵树，而我们知道，在学习 数据结构 中，做 OJ 题时经常会让我们做一件事，那就是 判断这棵树的根节点是否为空 ，因此，我们可以发现，一棵树也可以是空树，空树同样属于二叉搜索树。
除此之外， 二叉搜索树 还具有以下一些重要的性质：

• 如果 存在左树，则 左子树 中的所有结点中的值都比这个根节点的值要 小
• 如果 存在右数 ，则 右子树 中的所有结点中的值都比这个根节点的值要 大

2、如何轻松愉快地理解二叉搜索树中查找操作

所谓查找，在编程中有一个专业术语，那就是遍历，在我们学习二叉搜索树中，你需要知道一个二叉树很重要的一个遍历方法：双指针法，即需要一个

cur

指针和一个

parent

指针一起协同合作遍历整棵二叉搜索树，写成C++代码如下：

Node* cur = _root;
//cur指针是用来记录当前程序指向的结点

查找过程中你需要知道的一些东西

查找 的过程需要依赖 二叉搜索树 的一个很重要的 性质 ，就是 左子树中的结点都比根节点的值小，右子树中的结点的值都比根节点的值大 ，因此，在遍历的过程中，我们需要不断去 比较查找的值与当前结点的值的大小 这个时候就需要一个 循环 来帮助我们处理这个操作，查找的值比当前结点的值大，则向左子树移动，即去左子树找，查找的值比根节点的值大，则向右子树移动，即去右子树找

代码实现

显然，通过代码，我们很容易可以发现整个代码的逻辑非常简单，无非就是以下几个重点需要我们注意：

1. 判断当前查找的树是否为 空树 ，如果为 空树 ，则不需要继续向下查找，即返回false即可。如果查找的树不是空树，则继续执行第二步。
2. 遍历整棵树，知道找到所需要找到的值为止，前面介绍了一个很重要的。遍历方法，这里只需要一个cur指针就行了
3. 不断 比较查找的值与当前结点的值的大小 这个时候就需要一个 循环 来帮助我们处理这个操作，查找的值比当前结点的值大，则向左子树移动，即去左子树找，查找的值比根节点的值大，则向右子树移动，即去右子树找。
4. 如果整个循环结束之后还没找到与要查找的值相等，则说明该树中不存在相应的值，故此时需要返回false

3、如何闭着眼睛将二叉搜索树中的非递归删除操作清楚地浮现在脑海里

说到二叉搜索树的删除操作，相信很多初学者都会为之而感到头疼，因为里面涉及的相关内容相比于二叉搜索树中的其他操作都要复杂得多，实现起来需要100行代码左右，但是不要着急，通过以下大白话的讲解，相信你能突破二叉搜索树的删除操作

删除过程中你需要知道的一些东西

首先我们需要判断这棵树是否为空树，如果为空树，那当然是没法删除的，此时只需要返回

false

即可，如果不为空树，则进入下一个步骤，此时我们需要先找到要删除的结点的位置，才好删除嘛，而这个过程上面的经典的二叉搜索树的遍历方法（双指针法）就可以排上用场了，找到要删除的结点之后，需要对该节点进行分类讨论，相信大家都是合格的高中毕业生，分类讨论应该是难不倒大家的，具体情况如下：

1. 该节点为叶子结点，即没有左右孩子
2. 该节点只存在左孩子
3. 该节点只存在右孩子
4. 该节点同时存在左右孩子，这种情况下需要采用一个经典的方法来处理，即替换法

其实通过我们认真思考，我们不难发现，第一种情况是可以合并到第二种情况或者第三种情况中的，也就是说一共可以分为三种情况。

具体的代码实现与分析：

判断这棵树是否为空树，如果为空树，那当然是没法删除的，此时只需要返回

false

即可

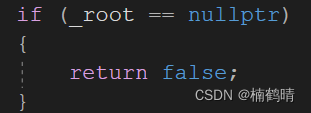
找到要删除的结点的位置（遍历）

不断 比较查找的值与当前结点的值的大小 这个时候就需要一个 循环 来帮助我们处理这个操作，查找的值比当前结点的值大，则向左子树移动，即去左子树找，查找的值比根节点的值大，则向右子树移动，即去右子树找

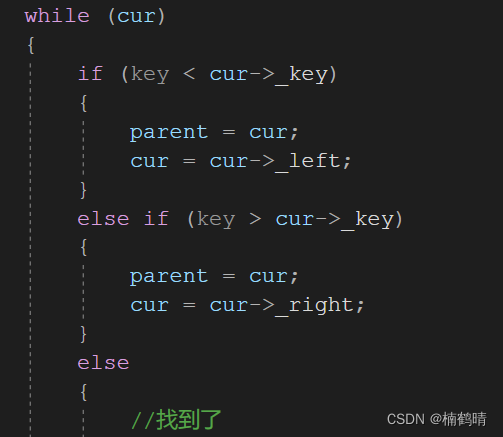
1、该节点只存在右孩子

1. 首先应该判断特殊的情况，即删除的结点是否为树的根节点，如果为树的根节点，则让根节点指向删除结点的右孩子（只有右孩子）
2. 如果不是，则先判断删除的结点是其父亲的左孩子还是其父亲的右孩子， 1.如果是其父亲的左孩子，则让其父亲的左指针指向删除结点的右孩子 2.如果是其父亲的右孩子，则让其父亲的右指针指向删除结点的右孩子

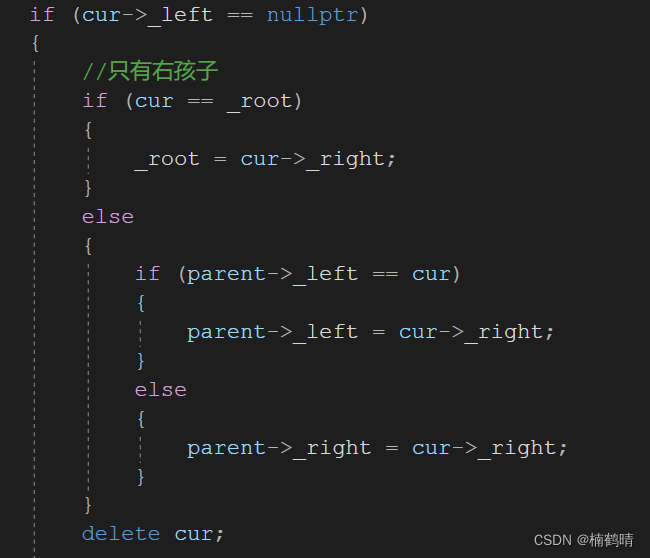
2、 该节点只存在左孩子

1. 判断特殊的情况，即删除的结点是否为树的根节点，如果为树的根节点，则让根节点指向删除结点的左孩子（只有左孩子）
2. 如果不是，则先判断删除的结点是其父亲的左孩子还是其父亲的右孩子， 1.如果是其父亲的左孩子，则让其父亲的左指针指向删除结点的左孩子 2.如果是其父亲的右孩子，则让其父亲的右指针指向删除结点的左孩子

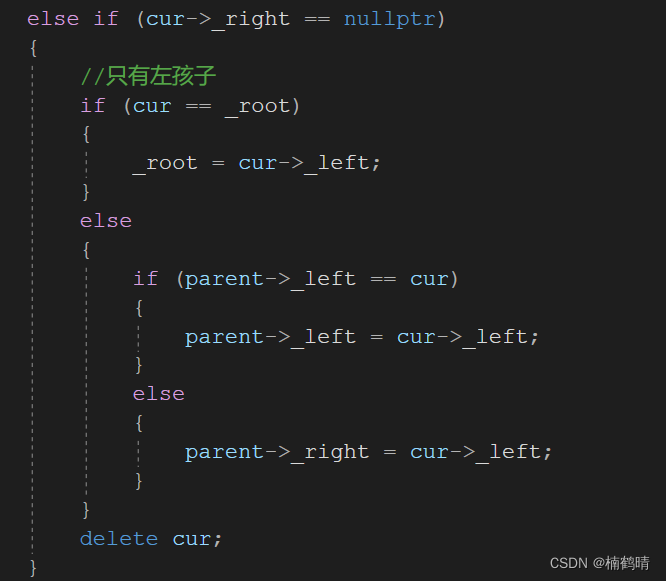
3、该节点同时存在左右孩子：这种情况下需要采用一个经典的方法来处理，即替换法。

1. 替换法即找到该节点的右子树中的最小值或者左子树中的最大值，然后替换掉要删除的结点中的值（这样做的目的在于替换完之后，仍然能够使整棵树保持二叉搜索树的性子，即左子树的所有结点都比根节点小，右子树中的所有结点都比根节点大）
2. 查找方法：这里以查找右子树中的最小值为例，首先从右子树的根节点出发，不断向左走，由二叉搜索树的性质我们不难发现，在一棵二叉搜索树中，越往左的值越小，越往右的值越大，因此，我们只需要找到删除结点的右子树中的最左边的结点的值即可，这里同样需要一个父亲结点来记录父亲结点的位置，在后面删除的操作中需要用到
3. 找到右子树中的最小结点即代码中的minRight之后就是删除操作了，与前面一样，需要先判断该结点是其父亲的左孩子还是其父亲的右孩子，逻辑与前面一样，这里需要注意，一般情况下，minRight只可能是minParent的左孩子，因为前面的循环一直是往左走的嘛，但是我们需要考虑一种特殊的场景：删除的结点即cur是整棵树的根节点，minRight是该节点右子树的第一个结点，此时minRight就是minParent的右孩子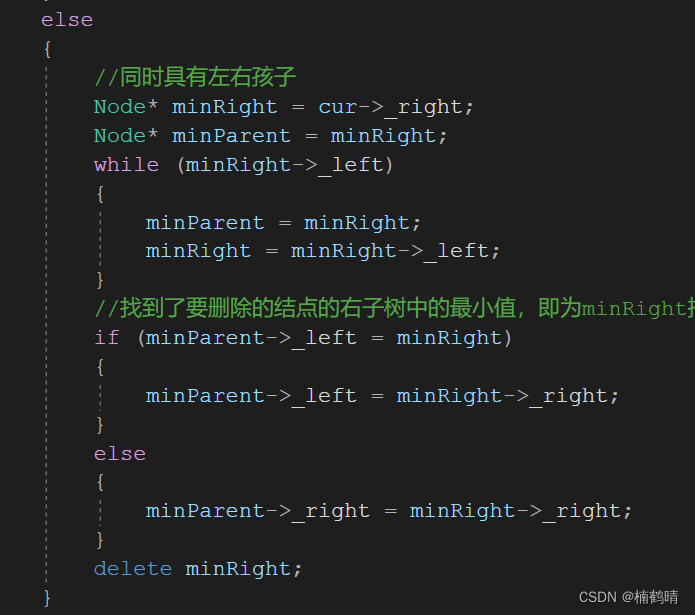

如果满足以上三种情况，则可以正常删除

否则，则说明在该树中不存在该值，则无法删除

4、在二叉搜索树的插入操作中那些你应该注意的事情

在经过上面删除操作的一番折腾之后，相信兄弟们差不多快要精疲力尽了，没事，现在我们再找个插入操作来放松放松，

插入操作中三步走

1. 判断该树是否为空树，如果为空树，则说明是插入一个结点，此时只需要直接插入到根节点即可
2. 如果该树不是空树，则应该先找到插入的位置（遍历），与上面的操作基本一致
3. 找到插入的位置之后就是要插入结点了，插入之前要先判断该值与插入位置的父亲结点的值的大小关系以决定是插入左树还是插入右树 1. 插入的值key比parent小，插入左树2. 插入的值key比parent大，插入右树

具体的代码实现与分析

1、判断该树是否为空树，如果为空树，则说明是插入一个结点，此时只需要直接插入到根节点即可

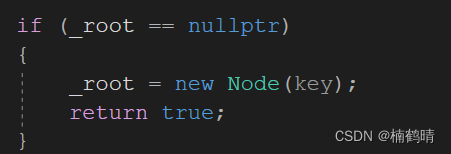
2、如果该树不是空树，则应该先找到插入的位置（遍历），与上面的操作基本一致

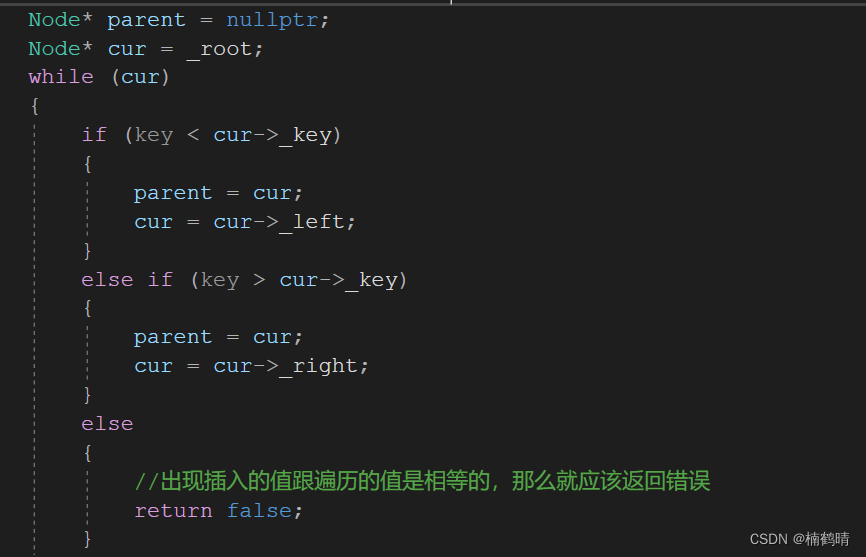
3. 找到插入的位置之后就是要插入结点了，插入之前要先判断该值与插入位置的父亲结点的值的大小关系以决定是插入左树还是插入右树

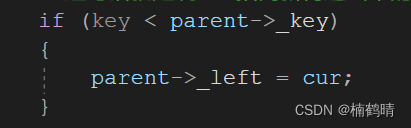
1. 插入的值`key`比`parent`小，插入左树

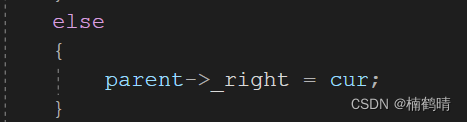
3. 插入的值`key`比`parent`大，插入右树

插入 操作的过程中需要注意，这个二叉搜索树版本是不支持插入再树中已经存在的值的，通过分析我们可以发现在插入的过程中其实能够潜在地帮助我们完成对数据的 去重 操作以及 排序 功能，我们只需要对这棵树进行一个简单的 中序遍历 ，即可实现数据的 升序 。