ARMA模型的性质之ARMA模型

一、ARMA模型的定义

具有如下结构的模型称为自回归移动平均模型，简记 ARMA(p,q)

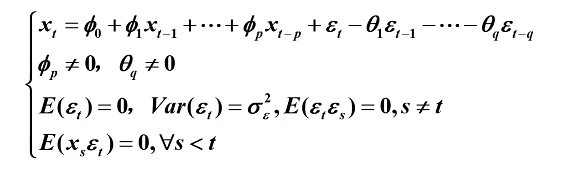
特别地当 时，称为中心化ARMA(p,q)模型

中心化ARMA(p,q)模型

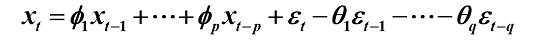
引进延迟算子，可记为

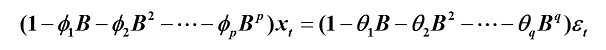
还可记为：

此时可简记为：

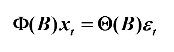
二、平稳条件与可逆条件

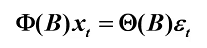
ARMA(p,q)模型的平稳条件

    **p阶**自回归模型系数多项式 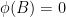![\phi (B)=0](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20%5Cphi%20%28B%29%3D0) 的根都在单位圆外

    即**ARMA(p,q)模型的平稳性**完全由其自回归部分的平稳性**决定**

ARMA(p,q)模型的可逆条件

** q阶**移动平均系数多项式 的根都在单位圆外

    即**ARMA(p,q)模型的可逆性**完全由其移动平滑部分的可逆性**决定**

三、传递形式与逆转形式

平稳可逆的ARMA(p,q)模型

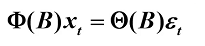
传递形式

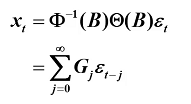
则可得：

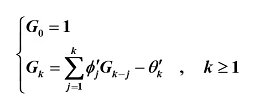
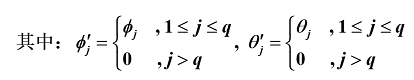
逆转形式：

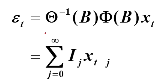
则有：

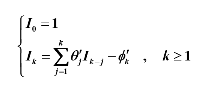
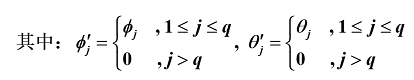
四、ARMA(p,q)模型的统计性质

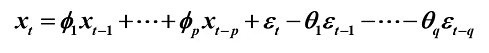
1.均值

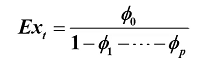
2.自协方差函数

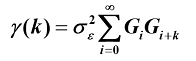
推导方式如下：

3.自相关系数

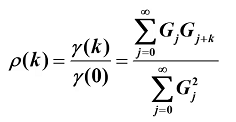
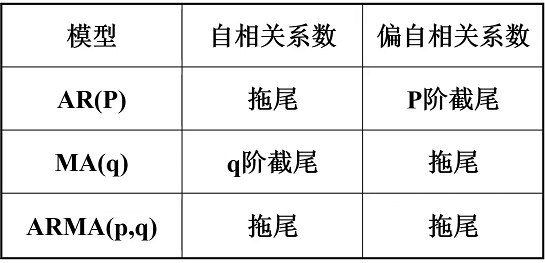
4.ARMA(p,q)模型自相关系数拖尾，偏自相关系数拖尾

举例：

要注意AR模型和MA模型的系数取值方式不同哦！！

x<-arima.sim(n=1000,list(ar=0.5,ma=-0.8))

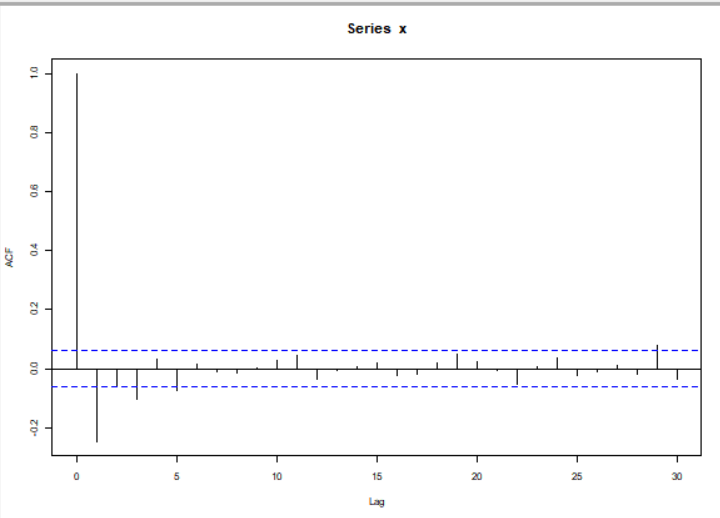
自相关系数图：

acf(X)

返回：

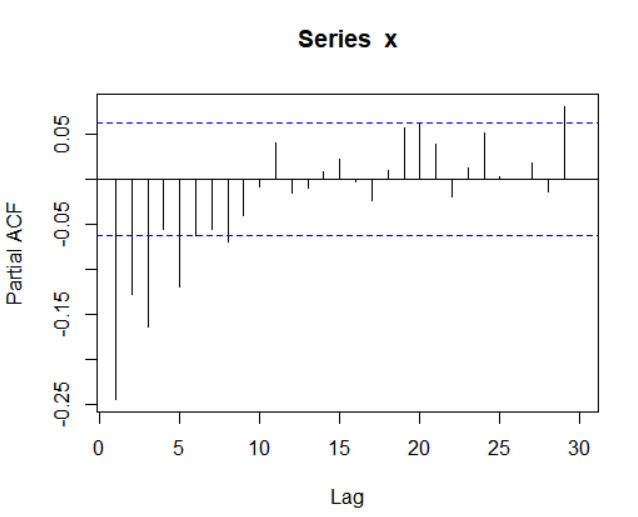
偏相关系数图：

pacf(x)

返回：

小结

中心化ARMA(p,q)模型

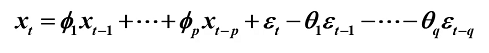
可简记为：

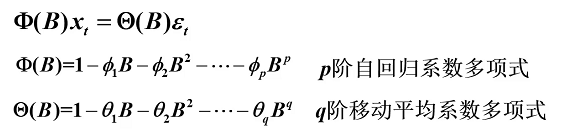
传递形式：

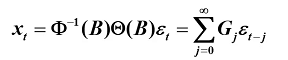
逆转形式：

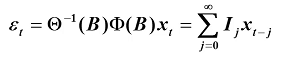
性质：