【数据挖掘】4、关联分析：Apriori、FP-Growth 算法、买面包是否也爱买啤酒

文章目录

关联规则这个概念，最早是由 Agrawal 等人在 1993 年提出的。在 1994 年 Agrawal 等人又提出了基于关联规则的 Apriori 算法，至今 Apriori 仍是关联规则挖掘的重要算法。

关联规则挖掘可以让我们从数据集中发现项与项（item 与 item）之间的关系，进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。

一、概念

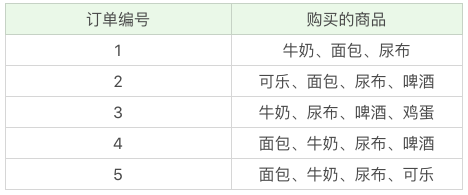
举一个超市购物的例子，下面是几名客户购买的商品列表：

1.1 支持度

支持度：是百分比，指某商品组合出现的次数 / 总次数，之间的比例。支持度越高则此组合出现的频率越大。

• “牛奶” 出现了 4 次，那么这 5 笔订单中 “牛奶” 的支持度就是 4/5=0.8。
• “牛奶 + 面包” 出现了 3 次，那么这 5 笔订单中 “牛奶 + 面包” 的支持度就是 3/5=0.6。

1.2 置信度

置信度是个条件概念，就是说在 A 发生的情况下，B 发生的概率是多少。

例如当你购买了商品 A，会有多大的概率购买商品 B

• 置信度（牛奶→啤酒）=2/4=0.5，代表如果你购买了牛奶，有多大的概率会购买啤酒？
• 置信度（啤酒→牛奶）=2/3=0.67，代表如果你购买了啤酒，有多大的概率会购买牛奶？
• 我们能看到，在 4 次购买了牛奶的情况下，有 2 次购买了啤酒，所以置信度 (牛奶→啤酒)=0.5，而在 3 次购买啤酒的情况下，有 2 次购买了牛奶，所以置信度（啤酒→牛奶）=0.67。

1.3 提升度

我们在做商品推荐的时候，重点考虑的是提升度，因为提升度代表的是“商品 A 的出现，对商品 B 的出现概率提升的”程度。

还是看上面的例子，如果我们单纯看置信度 (可乐→尿布)=1，也就是说可乐出现的时候，用户都会购买尿布，那么当用户购买可乐的时候，我们就需要推荐尿布么？

实际上，就算用户不购买可乐，也会直接购买尿布的，所以用户是否购买可乐，对尿布的提升作用并不大。我们可以用下面的公式来计算商品 A 对商品 B 的提升度：

      提升度 
     
    
      ( 
     
    
      A 
     
    
      → 
     
    
      B 
     
    
      ) 
     
    
      = 
     
    
      置信度 
     
    
      ( 
     
    
      A 
     
    
      → 
     
    
      B 
     
    
      ) 
     
    
      / 
     
    
      支持度 
     
    
      ( 
     
    
      B 
     
    
      ) 
     
    
   
     提升度 (A→B)= 置信度 (A→B)/ 支持度 (B) 
    
   
 提升度(A→B)=置信度(A→B)/支持度(B)

这个公式是用来衡量 A 出现的情况下，是否会对 B 出现的概率有所提升。所以提升度有三种可能：

• 提升度 (A→B)>1：代表有提升；
• 提升度 (A→B)=1：代表有没有提升，也没有下降；
• 提升度 (A→B)<1：代表有下降。

二、Apriori 算法

2.1 频繁项集的定义

我们看下 Apriori 算法是如何工作的：

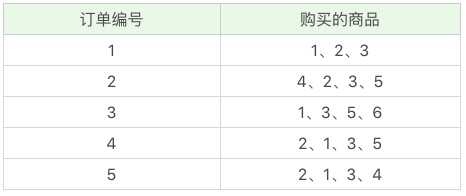
首先我们把上面案例中的商品用 ID 来代表，牛奶、面包、尿布、可乐、啤酒、鸡蛋的商品 ID 分别设置为 1-6，上面的数据表可以变为：

Apriori 算法其实就是查找频繁项集 (frequent itemset) 的过程，所以首先我们需要定义什么是频繁项集。

频繁项集就是支持度大于等于最小支持度 (Min Support) 阈值的项集，所以小于最小值支持度的项目就是非频繁项集，而大于等于最小支持度的项集就是频繁项集。

项集这个概念，英文叫做 itemset，它可以是单个的商品，也可以是商品的组合。我们再来看下这个例子，假设我随机指定最小支持度是 50%，也就是 0.5。

2.2 手动推导

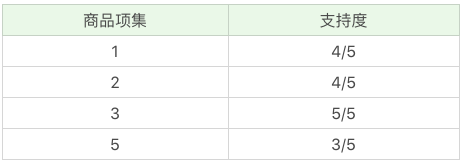
• 先计算单个商品的支持度，也就是得到 K=1 项的支持度，如下图：- 因为共 5 次订单，牛奶（商品编号为1）出现了 4 次，所以牛奶支持度为 4/5。- 因为共 5 次订单，面包（商品编号为2）出现了 4 次，所以面包支持度为 4/5。- 因为共 5 次订单，尿布（商品编号为3）出现了 5 次，所以尿布支持度为 5/5。- 因为共 5 次订单，可乐（商品编号为4）出现了 2 次，所以可乐支持度为 2/5。- 因为共 5 次订单，啤酒（商品编号为5）出现了 3 次，所以啤酒支持度为 3/5。- 因为共 5 次订单，鸡蛋（商品编号为6）出现了 1 次，所以鸡蛋支持度为 1/5。
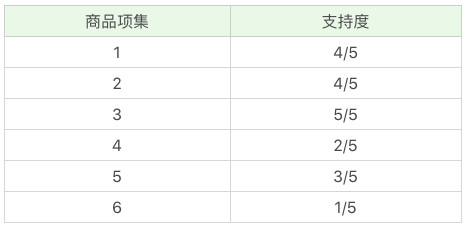
• 因为最小支持度是 0.5，所以你能看到商品 4、6 是不符合最小支持度的，不属于频繁项集，于是经过筛选商品的频繁项集就变成：
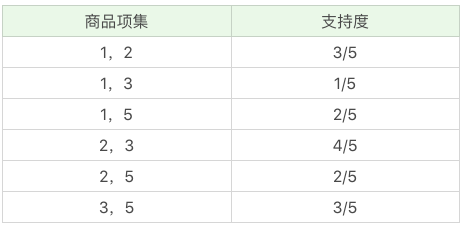
• 在这个基础上，我们将商品两两组合，得到 k=2 项的支持度：- 根据上文的最小支持度筛选，我们只考虑 1、2、3、5 号商品即可，即共有 1和2、1和3、1和5、2和3、2和5、3和5 这六种情况- 因为共 5 次订单，（商品编号为1和2）同时出现了 3 次，所以支持度为 3/5。- 因为共 5 次订单，（商品编号为1和3）同时出现了 4 次，所以支持度为 4/5。- 因为共 5 次订单，（商品编号为1和5）同时出现了 2 次，所以支持度为 2/5。- 因为共 5 次订单，（商品编号为2和3）同时出现了 4 次，所以支持度为 4/5。- 因为共 5 次订单，（商品编号为2和5）同时出现了 2 次，所以支持度为 2/5。- 因为共 5 次订单，（商品编号为3和5）同时出现了 3 次，所以支持度为 3/5。
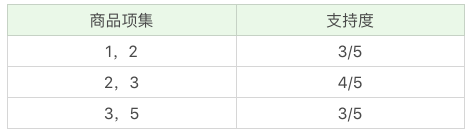
• 再筛掉小于最小值支持度的商品组合，可以得到：
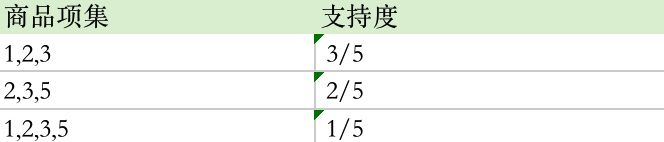
• 再将商品进行 K=3 项的商品组合，可以得到：- 根据上文的最小支持度筛选，我们只考虑 1和2、2和3、3和5 号商品即可，即共有 1和2和3、2和3和5、1和2和3和5 这三种情况- 因为共 5 次订单，（商品编号为1和2和3）同时出现了 3 次，所以支持度为 3/5。- 因为共 5 次订单，（商品编号为2和3和5）同时出现了 2 次，所以支持度为 2/5。- 因为共 5 次订单，（商品编号为1和2和3和5）同时出现了 1 次，所以支持度为 1/5。
• 再筛掉小于最小值支持度的商品组合，可以得到：
• 通过上面这个过程，我们可以得到 K=3 项的频繁项集{1,2,3}，也就是{牛奶、面包、尿布}的组合。
• 到这里，我们已经模拟了一遍整个 Apriori 算法的流程，其递归流程是：1. K=1，计算 K 项集的支持度；2. 筛选掉小于最小支持度的项集；3. 如果项集为空，则对应 K-1 项集的结果为最终结果。4. 否则 K=K+1，重复 1-3 步。

2.3 SDK 实战

关联规则挖掘在生活中有很多使用场景，不仅是商品的捆绑销售，甚至在挑选演员决策上，也能通过关联规则挖掘看出来某个导演选择演员的倾向。下文用 Apriori SDK 实战：

Apriori 虽然是十大算法之一，不过在 sklearn 工具包中并没有它，也没有 FP-Growth 算法。Python 的库可在 https://pypi.org/ 搜索。

调用方法如下：

# pip install efficient-apriori
itemsets, rules = apriori(data, min_support,  min_confidence)

• data 是我们要提供的数据集，它是一个 list 数组类型。
• min_support 参数为最小支持度，在 efficient-apriori 工具包中用 0 到 1 的数值代表百分比，比如 0.5 代表最小支持度为 50%。
• min_confidence 是最小置信度，数值也代表百分比，比如 1 代表 100%。

前文提到的概念回顾如下：

支持度：指的是某个商品组合出现的次数与总次数之间的比例。支持度越高，代表这个组合出现的概率越大。
置信度：是一个条件概念，就是在 A 发生的情况下，B 发生的概率是多少。
提升度：代表的是“商品 A 的出现，对商品 B 的出现概率提升了多少”。

2.3.1 超市购物

接下来，用上文提到的超市购物数据集如下图，运行结果如下：

from efficient_apriori import apriori # efficient-apriori 库把每一条数据集里的项式都放到了一个集合中进行运算，并没有考虑它们之间的先后顺序# 设置数据集
data =[('牛奶','面包','尿布'),('可乐','面包','尿布','啤酒'),('牛奶','尿布','啤酒','鸡蛋'),('面包','牛奶','尿布','啤酒'),('面包','牛奶','尿布','可乐')]# 挖掘频繁项集和频繁规则
itemsets, rules = apriori(data, min_support=0.5,  min_confidence=1)print(itemsets)# 频繁项集输出结果如下:{1:{('牛奶',):4,('面包',):4,('尿布',):5,('啤酒',):3},2:{('啤酒','尿布'):3,('尿布','牛奶'):4,('尿布','面包'):4,('牛奶','面包'):3},3:{('尿布','牛奶','面包'):3}}print(rules)# 关联关系输出结果如下:[{啤酒}->{尿布},{牛奶}->{尿布},{面包}->{尿布},{牛奶, 面包}->{尿布}]

2.3.2 挑选演员

2.3.2.1 爬虫

在实际工作中，数据集是需要自己来准备的，比如今天我们要挖掘导演是如何选择演员的数据情况，但是并没有公开的数据集可以直接使用。因此我们需要使用之前讲到的 Python 爬虫进行数据采集。

不同导演选择演员的规则是不同的，因此我们需要先指定导演。数据源我们选用豆瓣电影。

先来梳理下采集的工作流程。

首先我们先在https://movie.douban.com搜索框中输入导演姓名，比如“宁浩”。

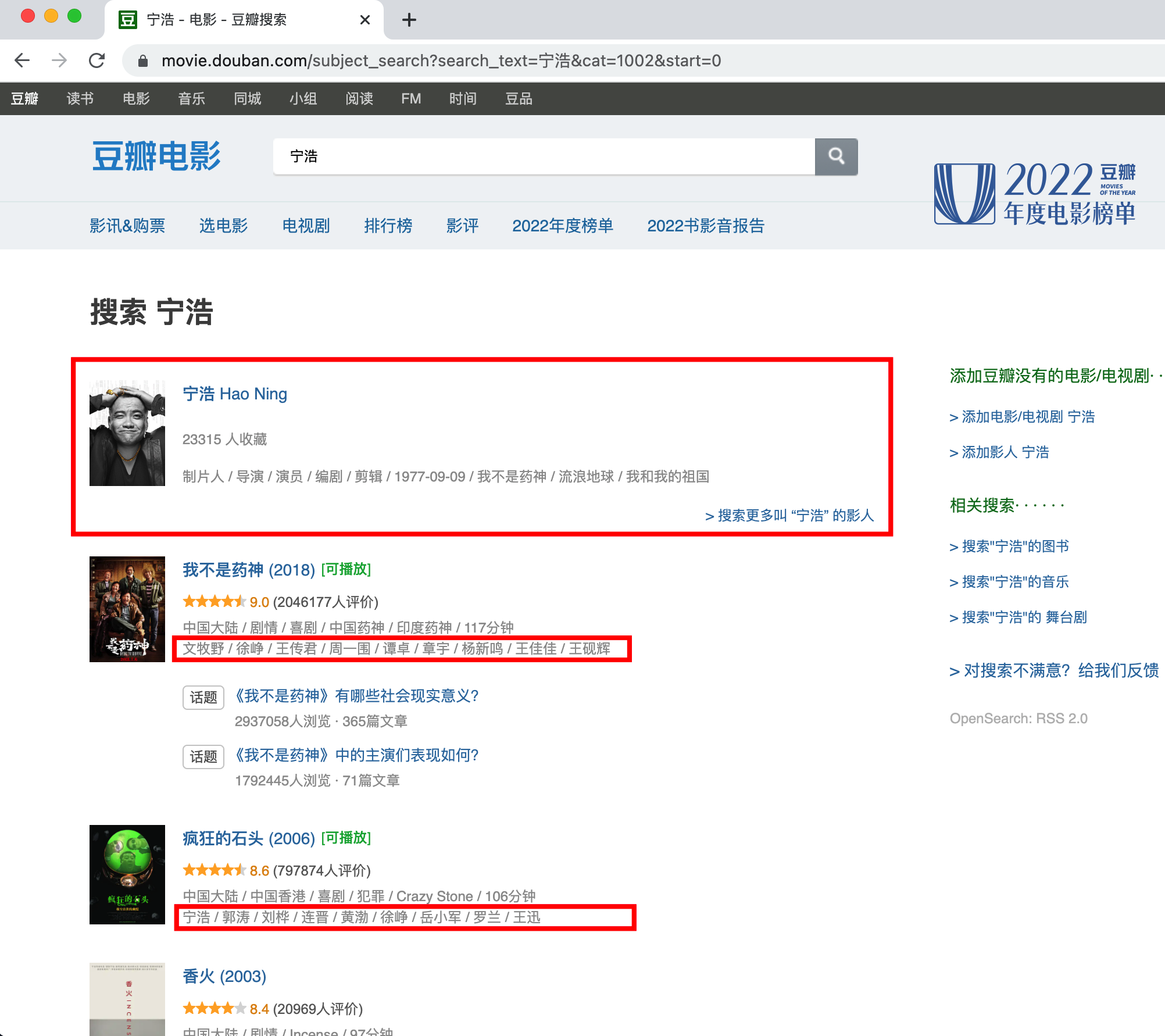
页面会呈现出来导演之前的所有电影，然后对页面进行观察，你能观察到以下几个现象：

• 页面默认是 15 条数据反馈，第一页会返回 16 条。因为第一条数据实际上这个导演的概览，你可以理解为是一条广告的插入，下面才是真正的返回结果。
• 每条数据的最后一行是电影的演出人员的信息，第一个人员是导演，其余为演员姓名。姓名之间用“/”分割。

下文即为宁浩导演的爬虫代码，其结果会保存在 csv 文件中：

# coding:utf-8# 下载某个导演的电影数据集from lxml import etree
import time
from selenium import webdriver
import csv

chrome_driver ="/Users/sunyuchuan/Downloads/chromn-download/chromedriver"
driver = webdriver.Chrome(executable_path=chrome_driver)# 设置想要下载的导演 数据集
director =u'宁浩'# 写 CSV 文件
file_name ='./'+ director +'.csv'
base_url ='https://movie.douban.com/subject_search?search_text='+ director +'&cat=1002&start='
out =open(file_name,'w', newline='', encoding='utf-8-sig')# utf-8-sig是防止中文乱码

csv_write = csv.writer(out, dialect='excel')
flags =[]# 下载指定页面的数据defdownload(request_url):
    driver.get(request_url)
    time.sleep(1)
    html = driver.find_element_by_xpath("//*").get_attribute("outerHTML")
    html = etree.HTML(html)# 设置电影名称，导演演员 的 XPATH
    movie_lists = html.xpath("/html/body/div[@id='wrapper']/div[@id='root']/div[1]//div[@class='item-root']/div[@class='detail']/div[@class='title']/a[@class='title-text']")
    name_lists = html.xpath("/html/body/div[@id='wrapper']/div[@id='root']/div[1]//div[@class='item-root']/div[@class='detail']/div[@class='meta abstract_2']")# 获取返回的数据个数
    num =len(movie_lists)if num >15:# 第一页会有 16 条数据# 默认第一个不是，所以需要去掉
        movie_lists = movie_lists[1:]
        name_lists = name_lists[1:]for(movie, name_list)inzip(movie_lists, name_lists):# 会存在数据为空的情况if name_list.text isNone:continue# 显示下演员名称print(name_list.text)
        names = name_list.text.split('/')# 判断导演是否为指定的 directorif names[0].strip()== director and movie.text notin flags:# 将第一个字段设置为电影名称
            names[0]= movie.text
            flags.append(movie.text)
            csv_write.writerow(names)print('OK')# 代表这页数据下载成功print(num)if num >=14:# 有可能一页会有 14 个电影# 继续下一页returnTrueelse:# 没有下一页returnFalse# 开始的 ID 为 0，每页增加 15
start =0while start <10000:# 最多抽取 1 万部电影
    request_url = base_url +str(start)# 下载数据，并返回是否有下一页
    flag = download(request_url)# flag为false即无下一页if flag:
        start = start +15else:break
out.close()print('finished')

运行后打印日志如下：

文牧野 / 徐峥 / 王传君 / 周一围 / 谭卓 / 章宇 / 杨新鸣 / 王佳佳 / 王砚辉
宁浩 / 郭涛 / 刘桦 / 连晋 / 黄渤 / 徐峥 / 岳小军 / 罗兰 / 王迅
宁浩 / 李强
宁浩 / 黄渤 / 徐峥 / 袁泉 / 周冬雨 / 陶慧 / 岳小军 / 沈腾 / 张俪
宁浩 / 徐峥 / 黄渤 / 余男 / 多布杰 / 王双宝 / 巴多 / 杨新鸣 / 郭虹
宁浩 / 黄渤 / 戎祥 / 九孔 / 徐峥 / 王双宝 / 巴多 / 董立范 / 高捷
黄渤 / 舒淇 / 王宝强 / 张艺兴 / 于和伟 / 王迅 / 李勤勤 / 李又麟
宁浩 / 雷佳音 / 陶虹 / 程媛媛 / 山崎敬一 / 郭涛 / 范伟 / 孙淳 / 刘桦
宁浩 / 黄渤 / 沈腾 / 汤姆·派福瑞 / 马修·莫里森 / 徐峥 / 于和伟 / 雷佳音 / 刘桦
申奥 / 张艺兴 / 金晨 / 周也 / 孙阳
宁浩 / 关宇 / 傅羽鸽 / 常爱军 / 郝宜珊
宁浩 / 刘德华 / 瑞玛·席丹 / 单立文 / 林熙蕾 / 周炜 / 刘漪琳 / 刘若清
黄渤 / 舒淇 / 王宝强 / 张艺兴 / 于和伟 / 王迅 / 李勤勤 / 李又麟
宁浩 / 达瓦 / 毕力格 / 戈利班
宁浩 / 雷佳音 / 易烊千玺 / 佟丽娅 / 黄晓明
OK
16
宁浩 / 黄渤 / 王柏伦 / 聂鑫 / 王迅 / 岳小军
宁浩 / 徐峥 / 陈思诚 / 闫非 / 彭大魔 / 邓超 / 俞白眉 / 葛优 / 黄渤 / 范伟 / 沈腾 / 张占义 / 王宝强
徐磊 / 宁浩 / 贾樟柯 / 张子贤 / 张婧仪
宁浩 / 姚晨 / 黄觉
张扬 / 雷佳音 / 周冬雨 / 陈赫 / 陶虹 / 郭涛 / 郭子睿 / 刘仪伟 / 沈腾
王子昭 / 于和伟 / 郭麒麟 / 倪虹洁 / 许恩怡 / 张子贤
宁浩 / 张子贤 / 李嘉宇 / 李世成 / 孙麒鹏 / 王晶晶
宁浩
李凯 / 吴镇宇 / 林雪 / 颖儿 / 王太利 / 连晋 / 彭波
徐磊 / 曾赠 / 温仕培 / 吴辰珵 / 赵大地 / 肖麓西 / 刘铠齐 / 尹航 / 马昙 / 郭志荣 / 周文哲 / 久美成列 / 何坦 / 岳宇阳 / 贾樟柯 / 宁浩 / 张子枫 / 郭麒麟 / 章宇 / 刘桦 / 韩昊霖 / 倪虹洁
钟澍佳 / 杜淳 / 马苏 / 李若嘉 / 武强 / 王德顺 / 李亚天 / 谢园 / 张殿伦
何澍培 / 何晟铭 / 蒋梦婕 / 高洋 / 吕佳容 / 王琳 / 汤镇业 / 汤镇宗 / 吴岱融
宁浩 / 葛优
叶烽 / 王自健 / 中孝介 / 宁浩 / 李东学 / 黄龄 / 宋丹丹 / 王雷 / 范明
OK
15
宁浩 / 蔡鹭 / 毕秀茹 / 唐笑笑
陈凯歌 / 张一白 / 管虎 / 薛晓路 / 徐峥 / 宁浩 / 文牧野 / 黄渤 / 张译 / 韩昊霖 / 杜江 / 葛优 / 刘昊然 / 宋佳 / 王千源
郭帆 / 吴京 / 屈楚萧 / 李光洁 / 吴孟达 / 赵今麦 / 隋凯 / 屈菁菁 / 张亦驰
乌尔善 / 安藤政信 / 张雨绮 / 游本昌 / 刘晓晔 / 徐冲 / 韩鹏翼 / 刘桦 / 宁浩
张一白 / 韩琰 / 李炳强 / 彭昱畅 / 张婧仪 / 梁靖康 / 周依然 / 张宥浩 / 郭丞 / 周游 / 黄觉
许知远 / 黄灯 / 鲁白 / 何多苓 / 高圆圆 / 杨扬 / 宁浩 / 葛兆光
张一白 / 徐静蕾 / 李亚鹏 / 王学兵 / 何洁 / 程伊 / 崔达治 / 岳小军 / 冯瓅
轩南 / 宋运成 / 陈小妹
管虎 / 冯小刚 / 许晴 / 张涵予 / 刘桦 / 李易峰 / 吴亦凡 / 梁静 / 白举纲
丁晟 / 王凯 / 马天宇 / 王大陆 / 余皑磊 / 林雪 / 吴樾 / 李梦 / 张艺上
许鞍华 / 叶德娴 / 刘德华 / 秦海璐 / 秦沛 / 黄秋生 / 王馥荔 / 朱慧敏 / 江美仪
吴宇森 / 宁浩 / 陆川 / 玛莉亚·嘉西亚·古欣娜塔 / 费利普·弥勒 / 拉吉库马尔·希拉尼 / 安德鲁斯·文森特·戈麦斯 / 瑞奇·梅塔
谢晋 / 陈凯歌 / 关锦鹏 / 侯咏 / 陆川 / 宁浩 / 张一白 / 王光利 / 黄蜀芹 / 王小帅 / 顾长卫 / 陈家林 / 姚明 / 刘璇 / 郭富城 / 孙俪 / 陶红 / 范伟 / 蒋勤勤 / 林保怡
毕赣 / 菅浩栋 / 王沐 / 尹昉 / 王子文 / 李雪琴 / 安德烈·卡瓦祖缇 / 刘伽茵
高合玮 / 周昊轩 / 焦雄屏 / 方励 / 姜文 / 张艺谋 / 让-雅克·阿诺 / 李冰冰 / 章子怡 / 顾长卫
OK
15
徐峥 / 王传君 / 周一围 / 谭卓 / 章宇 / 杨新鸣 / 文牧野 / 王砚辉
王小帅 / 李少红 / 徐静蕾 / 薛晓路 / 贾樟柯 / 陆川 / 宁浩 / 万玛才旦
周昊轩 / 徐元 / 梅雪风 / 赛人 / 任国源 / 康怡 / 江志强 / 方励 / 曹保平
陈可辛 / 郭富城 / 周迅 / 吴景滔 / 谢欣颖 / 张睿家 / 宁浩 / 宁岱
刘德华 / 张涵予 / 梁家辉 / 刘青云 / 佟丽娅 / 周冬雨 / 葛优 / 惠英红
OK
5
finished

运行后存储 csv 如下：

2.3.2.2 挖掘

有了数据之后，我们就可以用 Apriori 算法来挖掘频繁项集和关联规则，代码如下：

# coding:utf-8import os
from efficient_apriori import apriori
import csv
director =u'宁浩'
file_name ='/Users/abc/pythonProject/'+director+'.csv'print(os.path.exists(file_name))
f =open(file_name,'r', encoding='utf-8-sig')
lists = csv.reader(f)# 数据加载
data =[]for names in lists:
     name_new =[]for name in names:# 去掉演员数据中的空格
           name_new.append(name.strip())
     data.append(name_new[1:])# 挖掘频繁项集和关联规则
itemsets, rules = apriori(data, min_support=0.3,  min_confidence=1)print(itemsets)# 输出如下：{1:{('黄渤',):7,('徐峥',):6},2:{('徐峥','黄渤'):6}}print(rules)# 输出如下：[{徐峥}->{黄渤}]

可以看出，宁浩导演喜欢用徐峥和黄渤，并且有徐峥的情况下，一般都会用黄渤。你也可以用上面的代码来挖掘下其他导演选择演员的规律。

一般来说最小支持度常见的取值有0.5，0.1, 0.05。最小置信度常见的取值有1.0, 0.9, 0.8。可以通过尝试一些取值，然后观察关联结果的方式来调整最小值尺度和最小置信度的取值。

三、FP-Growth 算法

上文的Apriori 在计算的过程中有以下几个缺点：

• 可能产生大量的候选集。因为采用排列组合的方式，把可能的项集都组合出来了；
• 每次计算都需要重新扫描数据集，来计算每个项集的支持度。

所以 Apriori 算法会浪费很多计算空间和时间，为此提出了 FP-Growth 算法，并在工作中很常用，其特点是：

• 创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除，减少了存储空间。我稍后会讲解如何构造一棵 FP 树；
• 整个生成过程只遍历数据集 2 次，大大减少了计算量。

3.1 算法步骤

算法包括如下 3 步：

3.1.1 创建项头表

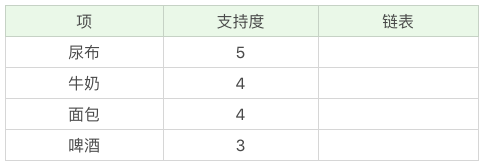
创建项头表的作用是为 FP 构建及频繁项集挖掘提供索引。

这一步的流程是先扫描一遍数据集，对于满足最小支持度的单个项（K=1 项集）按照支持度从高到低进行排序，这个过程中删除了不满足最小支持度的项。

项头表包括了项目、支持度，以及该项在 FP 树中的链表。初始的时候链表为空。

3.1.2 构造 FP 树

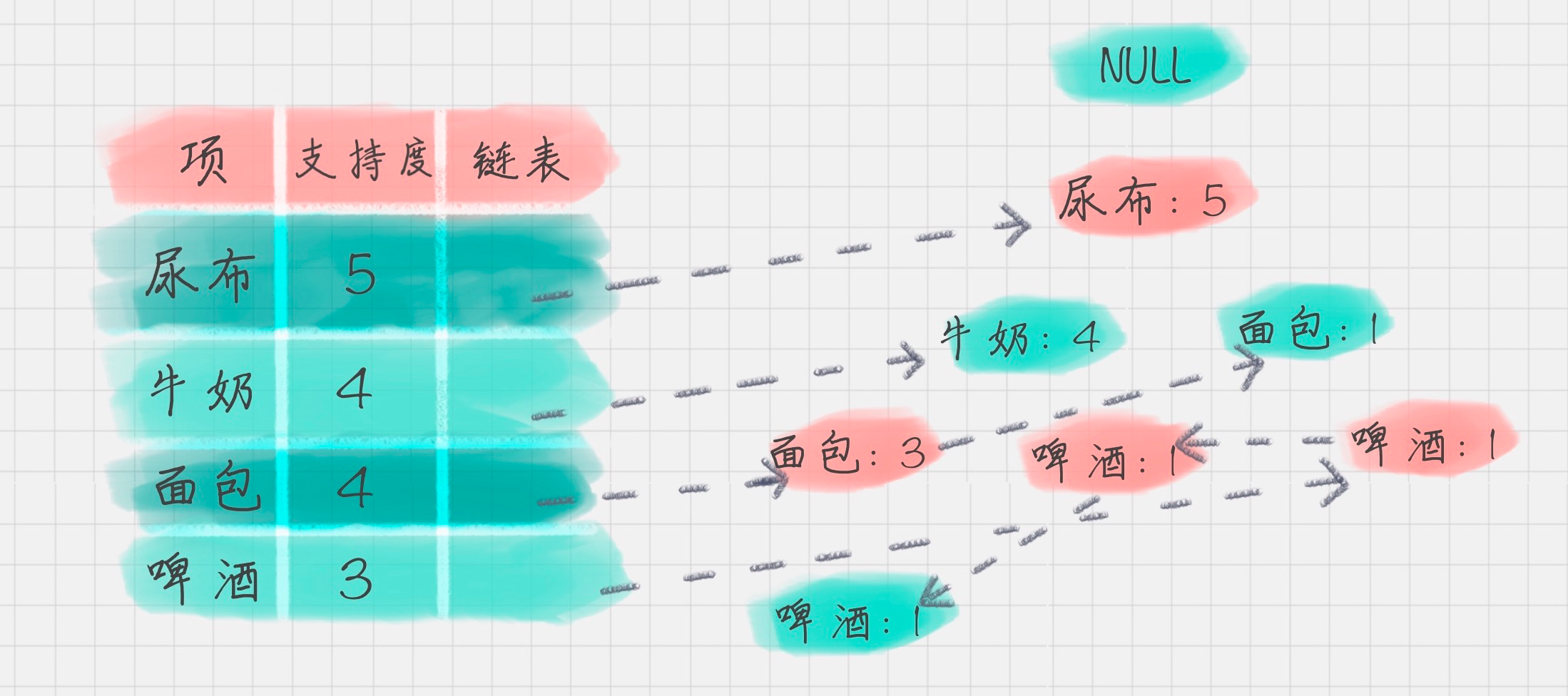
FP 树的根节点记为 NULL 节点。

整个流程是需要再次扫描数据集，对于每一条数据，按照支持度从高到低的顺序进行创建节点（也就是第一步中项头表中的排序结果），节点如果存在就将计数 count+1，如果不存在就进行创建。同时在创建的过程中，需要更新项头表的链表。

3.1.3 通过 FP 树挖掘频繁项集

到这里，我们就得到了一个存储频繁项集的 FP 树，以及一个项头表。我们可以通过项头表来挖掘出每个频繁项集。

具体的操作会用到一个概念，叫

条件模式基

，它指的是以要挖掘的节点为叶子节点，自底向上求出 FP 子树，然后将 FP 子树的祖先节点设置为叶子节点之和。

我以“啤酒”的节点为例，从 FP 树中可以得到一棵 FP 子树，将祖先节点的支持度记为叶子节点之和，得到：

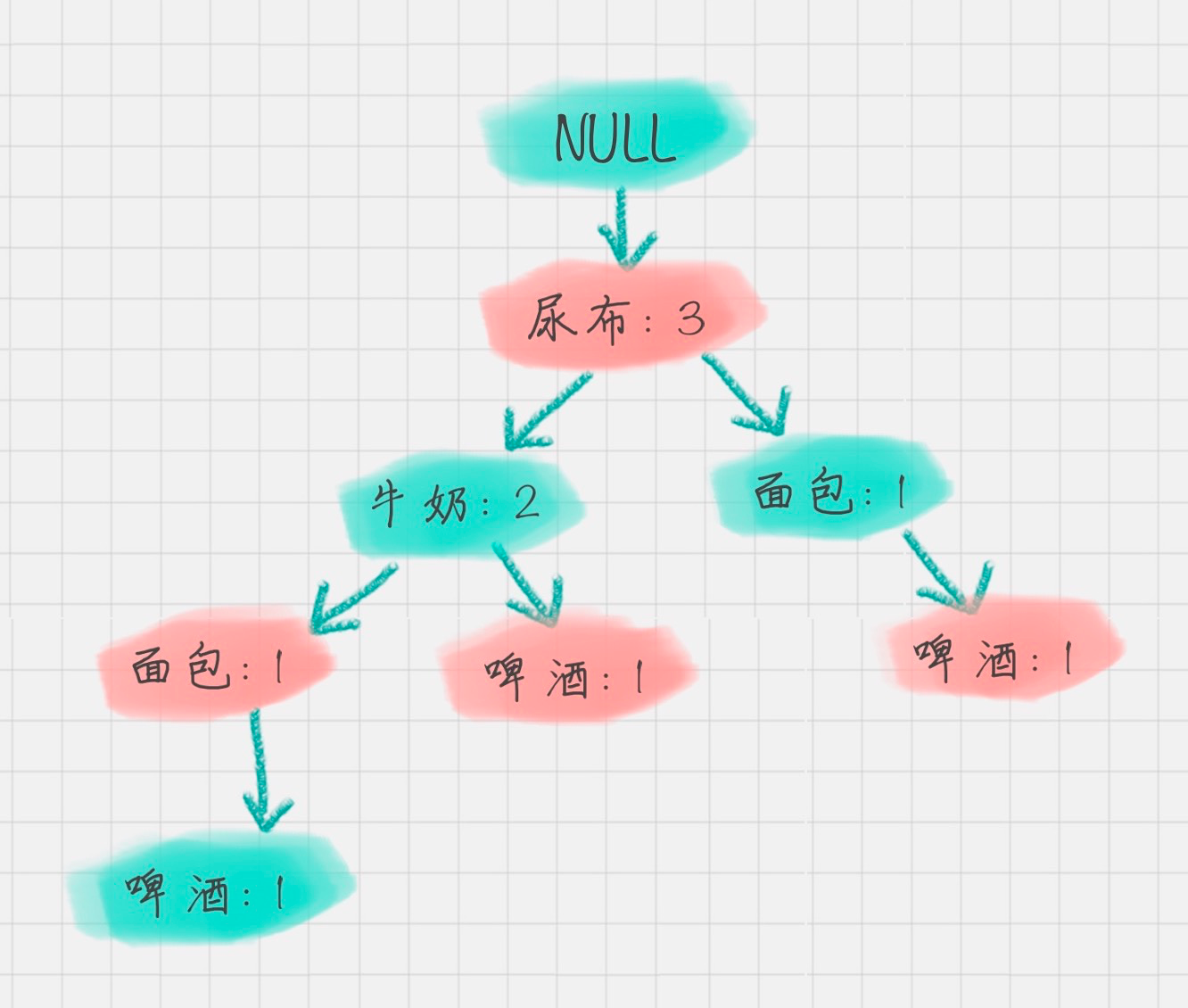
你能看出来，相比于原来的 FP 树，尿布和牛奶的频繁项集数减少了。

这是因为我们求得的是以“啤酒”为节点的 FP 子树，也就是说，在频繁项集中一定要含有“啤酒”这个项。

你可以再看下原始的数据，其中订单 1{牛奶、面包、尿布}和订单 5{牛奶、面包、尿布、可乐}并不存在“啤酒”这个项，所以针对订单 1，尿布→牛奶→面包这个项集就会从 FP 树中去掉，针对订单 5 也包括了尿布→牛奶→面包这个项集也会从 FP 树中去掉，所以你能看到以“啤酒”为节点的 FP 子树，尿布、牛奶、面包项集上的计数比原来少了 2。

条件模式基不包括“啤酒”节点，而且祖先节点如果小于最小支持度就会被剪枝，所以“啤酒”的条件模式基为空。

同理，我们可以求得“面包”的条件模式基为：

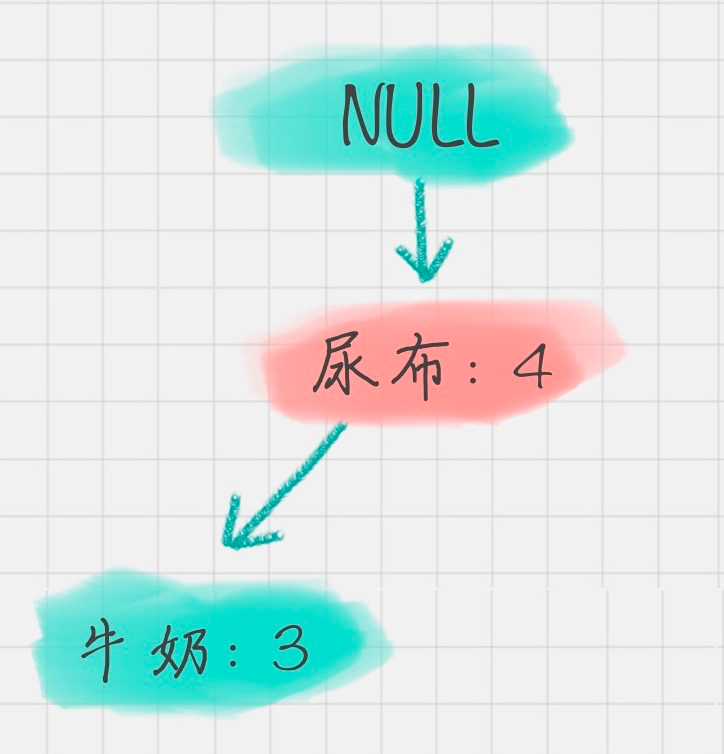
所以可以求得面包的频繁项集为{尿布，面包}，{尿布，牛奶，面包}。同样，我们还可以求得牛奶，尿布的频繁项集，这里就不再计算展示。

3.2 手动推导

参考视频讲解

• 通过 FP-Growth 算法，可以把频繁项集的挖掘 =》FP 树的挖掘，只需 O ( 2 ∗ N ) O(2*N) O(2∗N) 时间复杂度。

• 下例即为原始数据，其中有 9 笔事务，每笔事务有其项集。

3.2.1 计算单一项的频率（支持度计数）

扫描事务数据库，计算单一项的频率（支持度计数）

• 即 I1 项，共在 6 笔事务中出现（T100/400/500/700/800/900）
• …
• 即 I6 项，共在 1 笔事务中出现（T900）

3.2.2 按支持度和频率降序过滤事务，得到「频繁项1项集」

其中有如下要点：

• 按支持度过滤（丢弃非频繁的项）：即 支持度 > m i n S u p p o r t 支持度 > minSupport 支持度>minSupport
• 按频率降序排序，若频率相同则按字典序排列

对于本例，因为

     I 
    
   
     6 
    
   
  
    I6 
   
  
I6 不满足 minSupport 故被丢弃，另按频率降序排列后效果如下：

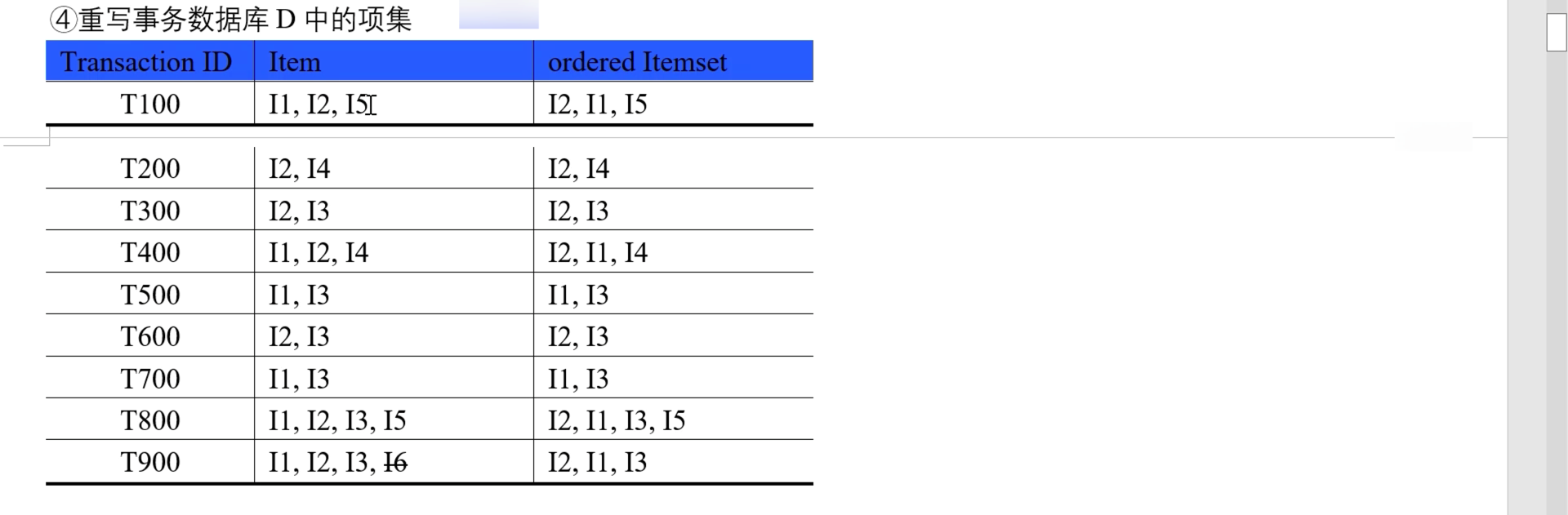
然后，按上文得到的频繁项1项集，重写事务数据库中的项集（即将各事务的项集，按频繁项1项集排序），效果如下图：

• 第一列是事务 ID，第二列是原事务中的项集，第三列是排序的频繁项1项集
• 以 T100 为例，其原事务中的相机为 {I1, I2, I5}，而上文的到的频繁项集排序是 {I2 > I1 > I3 > I4 > I5}，所以排序后 T100 的频繁项1项集为 {I2, I1, I5}。
• …
• 以 T900 为例，其原事务中的相机为 {I1, I2, I3, I6}，而上文的到的频繁项1项集排序是 {I2 > I1 > I3 > I4 > I5}，所以删除其 I6 项，并排序后，T100 的频繁项集为 {I2, I1, I3}。

3.2.3 构建FP树和项头表

3.2.3.1 构建FP树

逐行遍历各事务，构造 FP 树，其中新节点初始化频率为 1，已有的节点更新频率为「加1」。

• 首先，处理事务 T100，按 {I2, I1, I5} 的顺序插入 FP 树，效果如下图（其中「I2: 1」表示「I2 出现了 1 次」）：

• 其次，处理事务 T200，按 {I2, I4} 的顺序插入 FP 树，效果如下图：

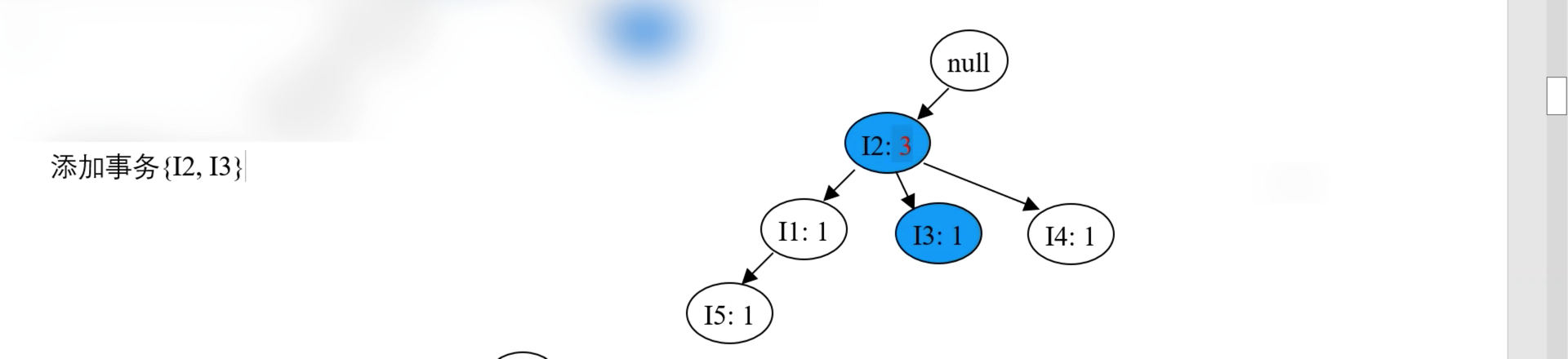
• 再处理事务 T300，按 {I2, I3} 的顺序插入 FP 树，效果如下图：

• 再处理事务 T400，按 {I2, I1, I4} 的顺序插入 FP 树，效果如下图：

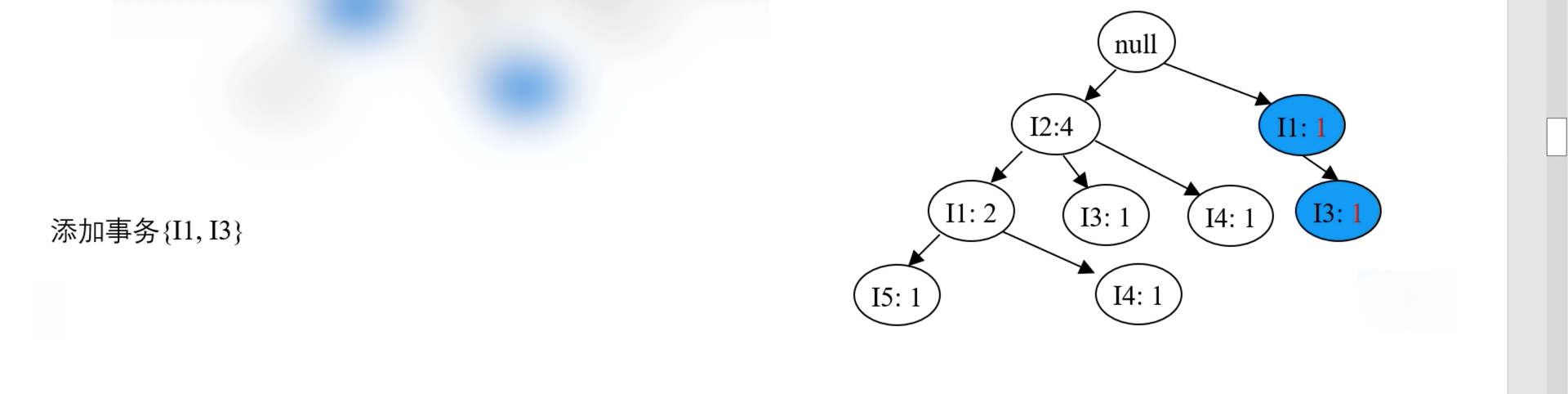
• 再处理事务 T500，按 {I1, I3} 的顺序插入 FP 树，从 root 节点开始，新建一个分支，效果如下图：

• 再处理事务 T600，按 {I2, I3} 的顺序插入 FP 树，效果如下图：

• 再处理事务 T700，按 {I1, I3} 的顺序插入 FP 树，效果如下图：

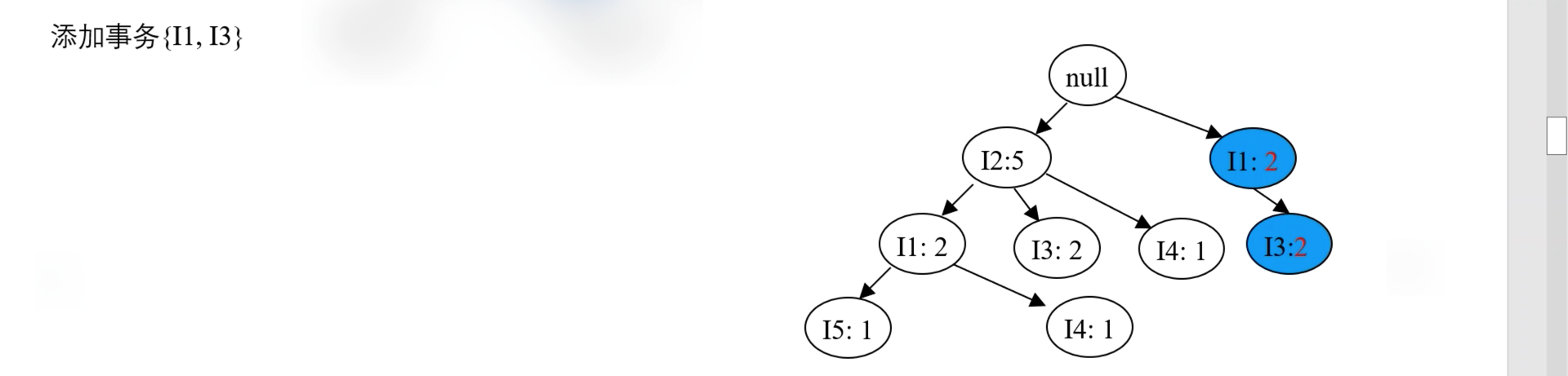
• 再处理事务 T800，按 {I2, I1, I3, I5} 的顺序插入 FP 树，效果如下图：

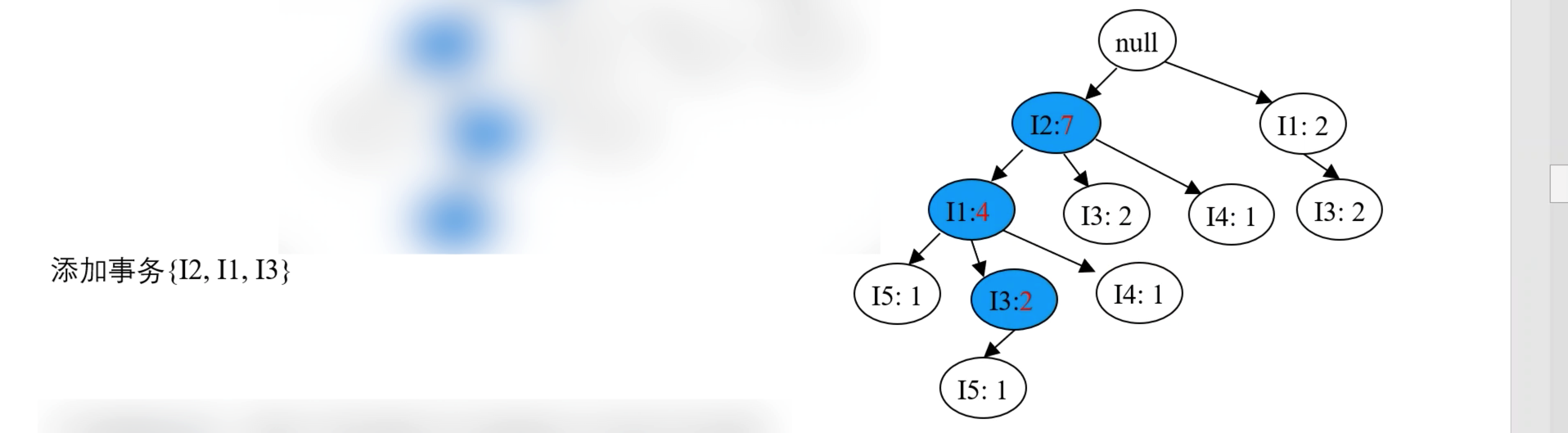
• 再处理最后一个事务 T900，按 {I2, I1, I3} 的顺序插入 FP 树，效果如下图：

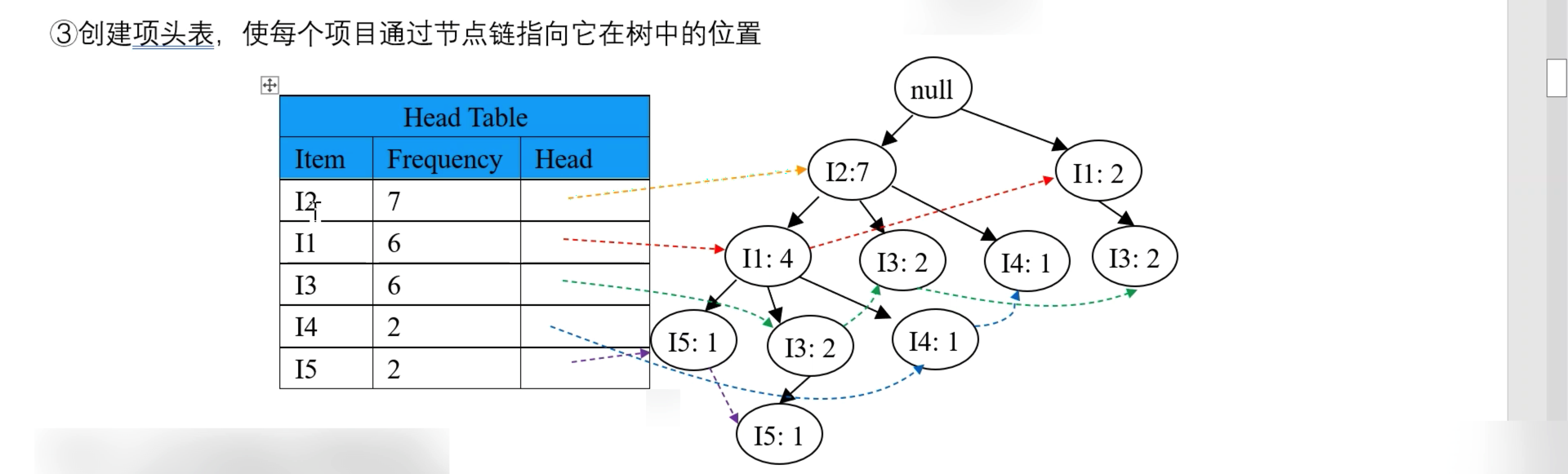
3.2.3.2 构建项头表

将 Step2 中得到的频繁项1项集中，添加 Head 列，其是一个链表，指向该 Item 在树中的位置，效果如下：

3.2.4 挖掘FP树生成频繁项集

下左图是输入的 「FP 树」，下右图是输出的 「条件 FP 树」，挖掘过程是按频率由低到高顺序的：

3.2.4.1 首先处理最低频率的 I5 项

首先处理最低频率的 I5，在 FP 树中找到两项 I5，找出从 root 到这两项 I5 之间的路径，分别为 {root => I2 => I1 => I5} 和 {root => I2 => I1 => I3 => I5}，其中记录节点频率（从叶子结点向上，根据父节点子节点之和的原则：则先两个 I5 各出现一次，再 I3 出现一次，再 I1 和 I2 出现两次）。

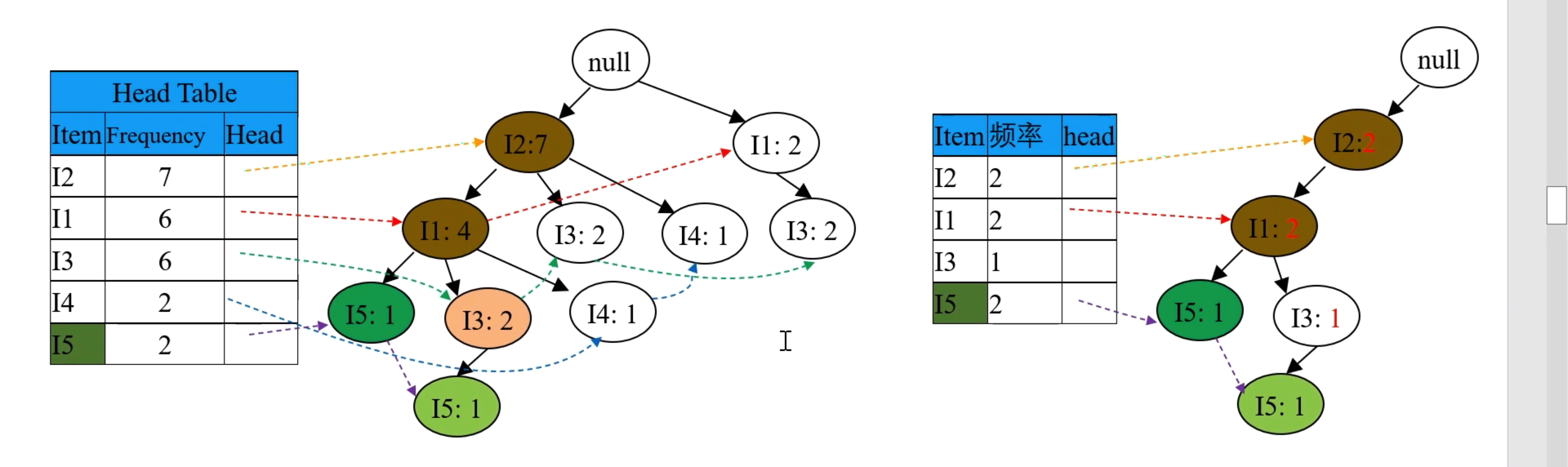
所以根据上右图的路径，记录 I5 的条件模式基（含义即就是前缀路径，其中不含叶子结点本身）为 {{I2 I1: 1}, {I2 I1 I3: 1}}，如下图：

因为其中 I3 频率不满足 minSupport 故被删掉，则条件 FP 树（即右上图中蓝色节点，其是由条件模式基按 minSupport 筛选得到的路径，其不含叶子节点和被删掉的点）为 <I2: 2, I1: 2>，如下图：

所以频繁项集为，叶子结点（I5） 和 条件 FP 树（<I2: 2, I1: 2>）的组合，即 {I2 I5: 2}, {I1 I5: 2}, {I2 I1 I5: 2}，如下图：

3.2.4.2 其次处理次低频率的 I4 项

其次处理次低频率的 I4，在 FP 树中找到两项 I4，找出从 root 到这两项 I4 之间的路径，分别为 {root => I2 => I4} 和 {root => I2=> I1 => I4}，其中记录节点频率（从叶子结点向上，根据父节点子节点之和的原则：则先两个 I4 各出现一次，再 I1 出现一次，再 I2 出现两次）。如下图：

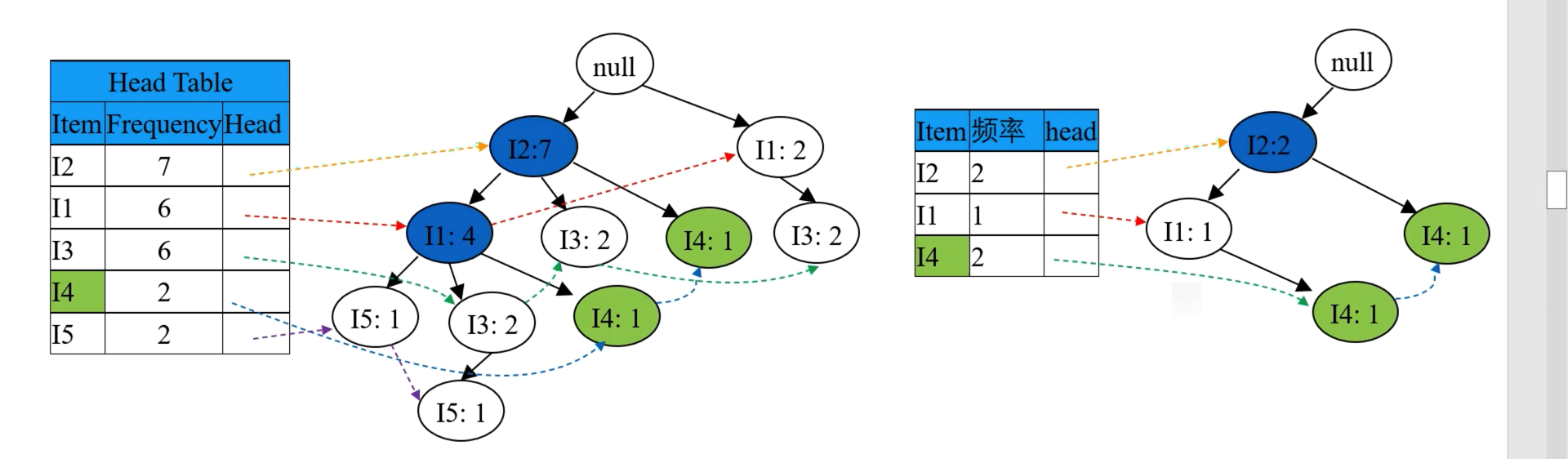
根据上右图的路径，记录 I4 的条件模式基（含义即就是前缀路径，其中不含叶子结点本身）为 {{I2 I1: 1}, {I2: 1}}，如下图：

因为其中 I1 频率不满足 minSupport 故被删掉，则条件 FP 树（即右上图中蓝色节点，其是由条件模式基按 minSupport 筛选得到的路径，其不含叶子节点和被删掉的点）为 <I2: 2>，如下图：

所以频繁项集为，叶子结点（I4） 和 条件 FP 树（<I2: 2>）的组合，即 {I2 I4: 2} 如下图：

3.2.4.3 其次处理中等频率的 I3 项

其次处理次低频率的 I3，在 FP 树中找到两项 I3，找出从 root 到这两项 I3 之间的路径，分别为 {root => I2 => I3} 和 {root => I2=> I1 => I3} 和 {root => I1 => I3}。其中记录节点频率（从叶子结点向上，根据父节点子节点之和的原则：则先三个 I3 各出现两次，再两个 I1 各出现两次，再 I4 出现四次），如下图：

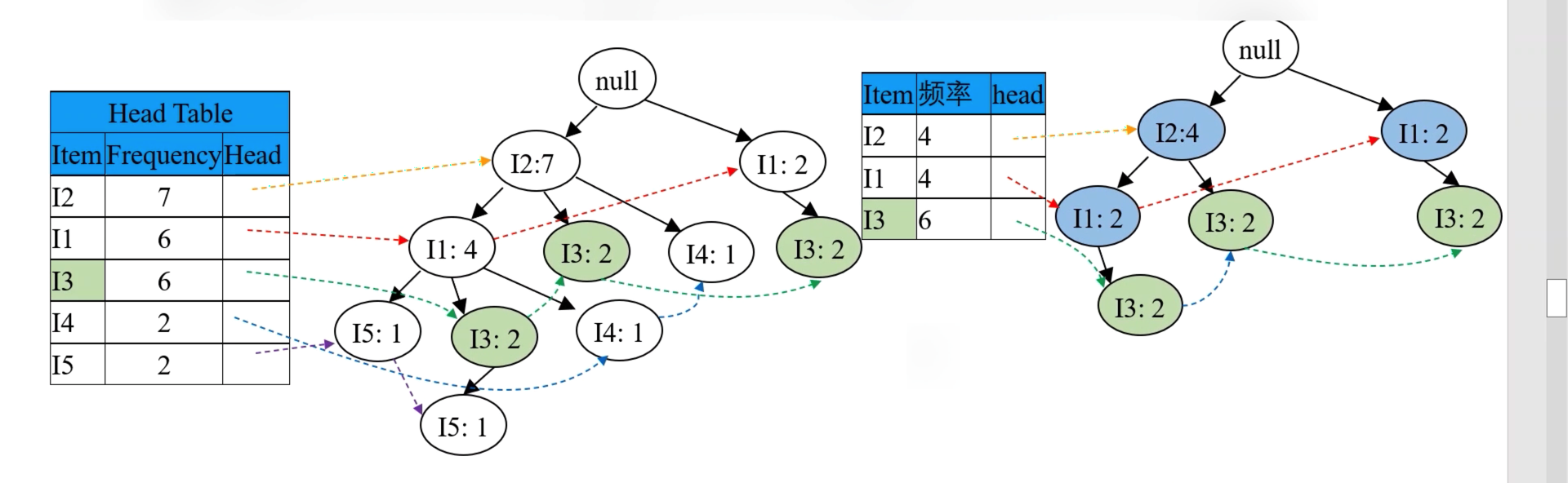
根据上右图的路径，记录 I3 的条件模式基（含义即就是前缀路径，其中不含叶子结点本身）为 {{I2 I1: 1}, {I2: 1}, {I1: 2}}，如下图：

因为其中 均满足 minSupport 不需删节点，则条件 FP 树（即右上图中蓝色节点，其是由条件模式基按 minSupport 筛选得到的路径，其不含叶子节点和被删掉的点）为 <I2: 4：I1: 2>, <I1: 2>，如下图：

所以频繁项集为，叶子结点（I3） 和 条件 FP 树（<I2: 4：I1: 2>, <I1: 2>）的组合，即 {I2 I4: 2} 如下图：

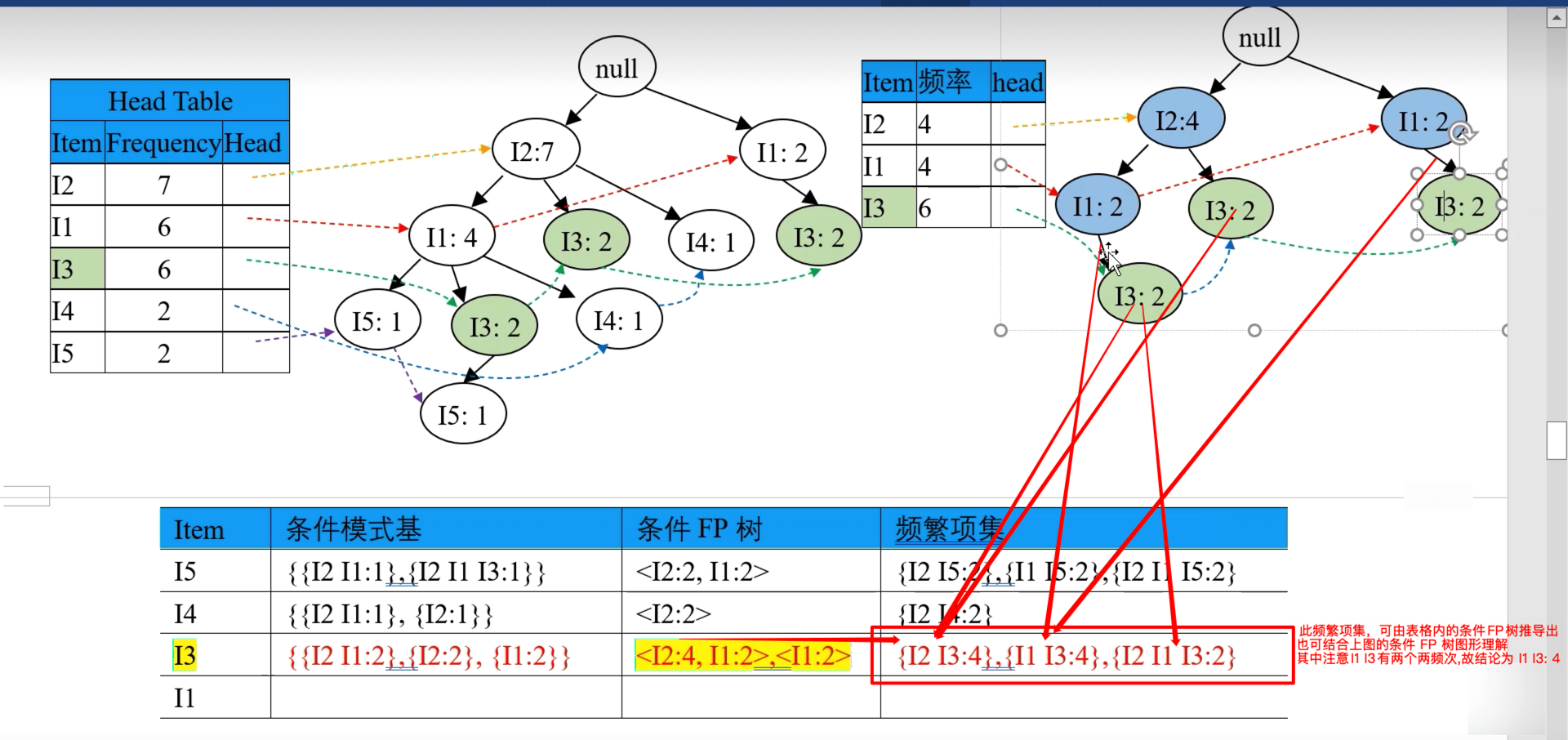
• 此频繁项集，可由表格内的条件FP树推导出，也可结合上图的条件 FP 树图形理解
• 其中注意 I2 I3 有 {I2 => I1 => I3} 和 {I2 => I3} 两条路径, 故结论是频繁项集为 I2 I3: 4，其意为 I2 和 I3 共同作为频繁项集出现了 4 次。
• 其中注意 I1 I3 有 {I2 => I1 => I3} 和 {I1 => I3} 两条路径, 故结论是频繁项集为 I1 I3: 4，其意为 I1 和 I3 共同作为频繁项集出现了 4 次。
• 其中注意 I2 I1 I3 有 {I2 => I1 => I3} 一条路径, 故结论是频繁项集为 I2 I1 I3: 2，其意为 I2 和 I1 和 I3 共同作为频繁项集出现了 2 次。

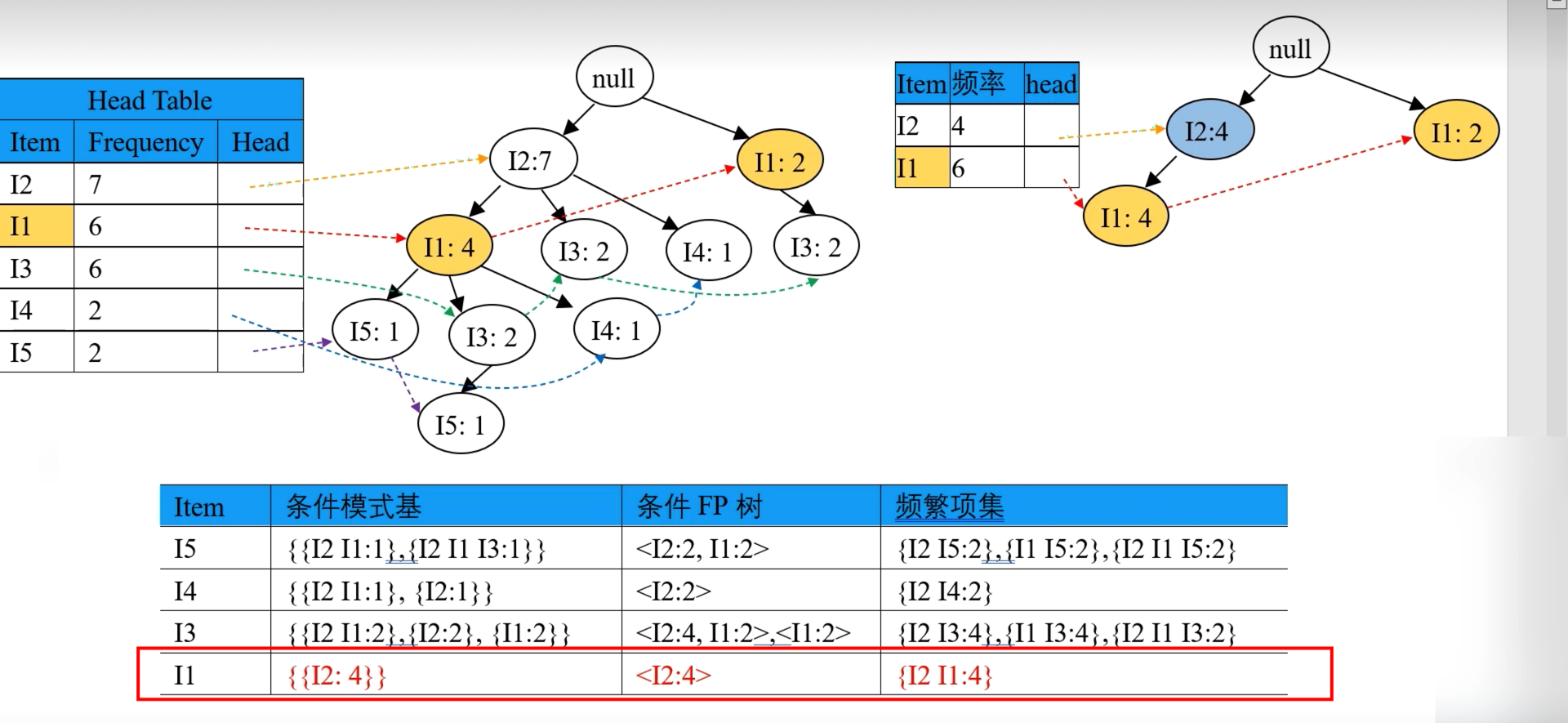
3.2.4.4 其次处理次高频率的 I1 项

处理过程如下：

3.2.4.5 最终得到全部频繁项集

最终，得到了频繁项集如下表：

3.3 总结

这里我们对FP Tree算法流程做一个归纳。FP Tree算法包括以下几步：

1. 扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。
2. 扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。
3. 读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。
4. 从项头表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项项的频繁项集（可以参见第4节对F的条件模式基的频繁二项集到频繁5五项集的挖掘）。
5. 如果不限制频繁项集的项数，则返回步骤4所有的频繁项集，否则只返回满足项数要求的频繁项集。

FP Tree算法改进了Apriori算法的I/O瓶颈，巧妙的利用了树结构，这让我们想起了BIRCH聚类，BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。

在实践中，FP Tree算法是可以用于生产环境的关联算法，而Apriori算法则做为先驱，起着关联算法指明灯的作用。除了FP Tree，像GSP，CBA之类的算法都是Apriori派系的。

参考 FP-Growth 树算法步骤图解

3.4 案例实战

网络上有很多实战案例：
github 的 topic
spark
综述