0
0

C语言描述数据结构 —— 二叉树(3)前、中、后序遍历

1.二叉树的性质

我们介绍过了完全二叉树，并且实现了堆用顺序结构存储的数据结构。现在要介绍的是普通的二叉树，即不满足完全二叉树的特性，也就是说，节点不是依次从左至右连续存储的，例如：

这样一颗二叉树就不是完全二叉树， 如果使用顺序结构存储的话，那么它的物理空间是这样的，它的存储空间是不连续的。

那么对于这样的结构，增删查改就没有意义了，因为要进行数据的存储、删除时为何不适用结构更简单的数组或者链表呢？并且如果要访问每一个节点的话还找不出什么规律，所以才要学习前序、中序、后序遍历。我们前面说过，二叉树是递归定义的，即任何一颗二叉树要不是空树，要不就分为根、左子树、右子树。

我们要有这么一个思想：二叉树只存在一个节点，那就是根节点；还存在两颗子树，分别为左子树和右子树；那么左子树也是一颗二叉树，这个二叉树只存在一个节点，那就是根节点，还存在两颗子树，分别为左子树和右子树；右子树也是一颗二叉树……这么理解，就可以知道什么是递归定义了。

我们再聊一聊没有增删查改的意义那么我们学习的目的是什么？有一种树叫做二叉搜索树：

当然这种二叉树是以后要学习的东西，而现在介绍的仅仅是为了以后的学习打好基础。

好我们回到正题，根据前面我们学习到的数据结构，我们可以推出下面几个性质：

    **1.一颗非空二叉树的第k层最多有2^(k-1)个结点**

这是很容易理解的，前面我们推导过完全二叉树的每一层有多少个结点，现在介绍的是普通二叉树，也就是非最后一层的父结点未必都有左孩子和右孩子。

    **2.一颗非空二叉树，假设层数为k，那么****最大结点数为2^k-1**

我们在介绍完全二叉树时也计算过满二叉树结点之和，普通二叉树的每个结点位置并不是都有结点。

    **3. 对任何一棵二叉树,  如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有**

n0＝n2 ＋1

我们可以找几个例子验证这样的结论：

    4. 如果是顺序结构存储的话，那么有：

    **父结点的下标=(孩子结点的下标-1)/2**

** 左孩子结点的下标=父结点的下标2+1*

** 右孩子结点的下标=父结点的下标2+2*

这些公式我们在实现堆的时候描述过。

下面就是做题巩固这些性质了。

1.某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）

A 不存在这样的二叉树

B 200

C 198

D 199

答案：B，根据公式推算即可。

2.下列数据结构中，不适合采用顺序存储结构的是（ ）

A 非完全二叉树

B 堆

C 队列

D 栈

答案：A，非完全二叉树用顺序结构存储的话空间是不连续的。队列虽然不推荐用顺序结构实现，但如果要实现的话，也比实现非完全二叉树强。

3.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）

A n

B n+1

C n-1

D n/2

答案：A，二叉树中的结点只有三类：度为2的，度为1的，度为0的。那么表达式就为n0+n1+n2=2n，而n0=n2+1，所以2n0-1+n1=2n，又因为2n和2n0的结果只能是偶数，所以n1必定为1。由此计算得，n0=n。

4.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ ）

A 11

B 10

C 8

D 12

答案：
B，完全二叉树的结点个数的取值范围为2^(k-1)到2^k-1，2^(10-1)=512,2^10-1=1023，符合范围。

5.一个具有767个节点的完全二叉树，其叶子节点个数为（）

A 383

B 384

C 385

D 386

答案：B，n0+n1+n2=767，根据公式可得2n0-1+n1=767,即2n0+n1=768，2n0得结果只能是偶数，所以n1必定为0。由此可以推出一个结论，完全二叉树中度为1的节点只有1个或者0个。

2.前序、中序、后序遍历

我们刚才提到二叉树是递归定义的，那么要遍历二叉树也需要使用递归的方法。注意一定要牢记我们的递归思想。 那么这三个遍历规则是什么呢？

  • 前序遍历：先访问根节点，其次访问左子树，最后访问右子树
  • 中序遍历：先访问左子树，其次访问根节点，最后访问右子树
  • 后序遍历：先访问左子树，其次访问右子树，最后访问根节点

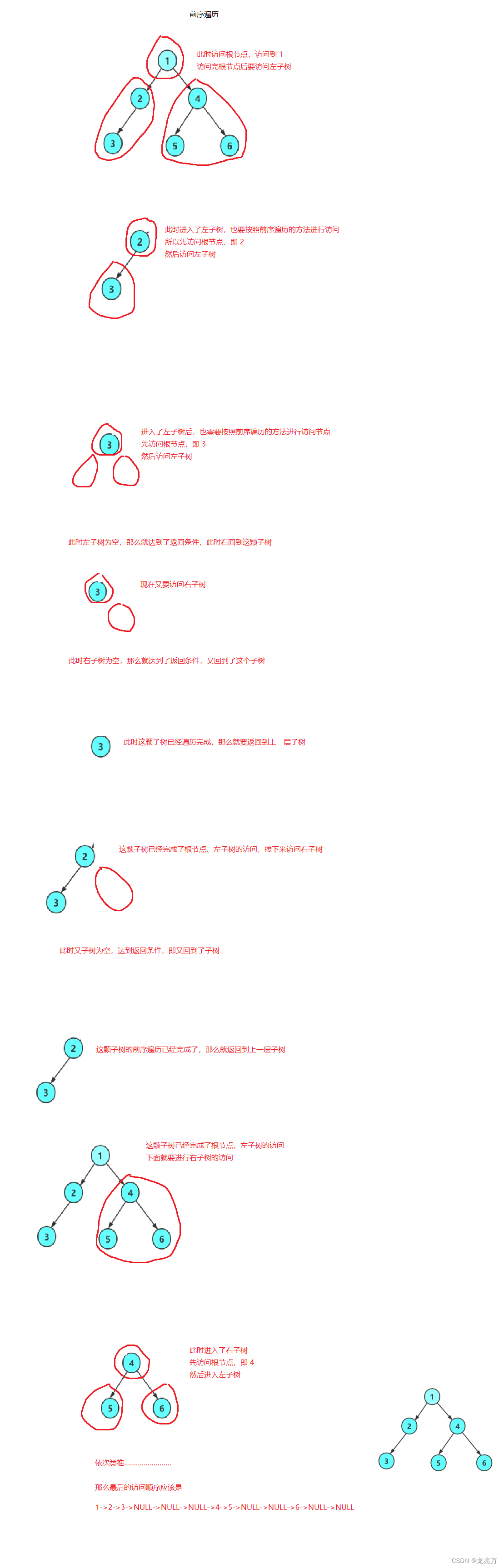
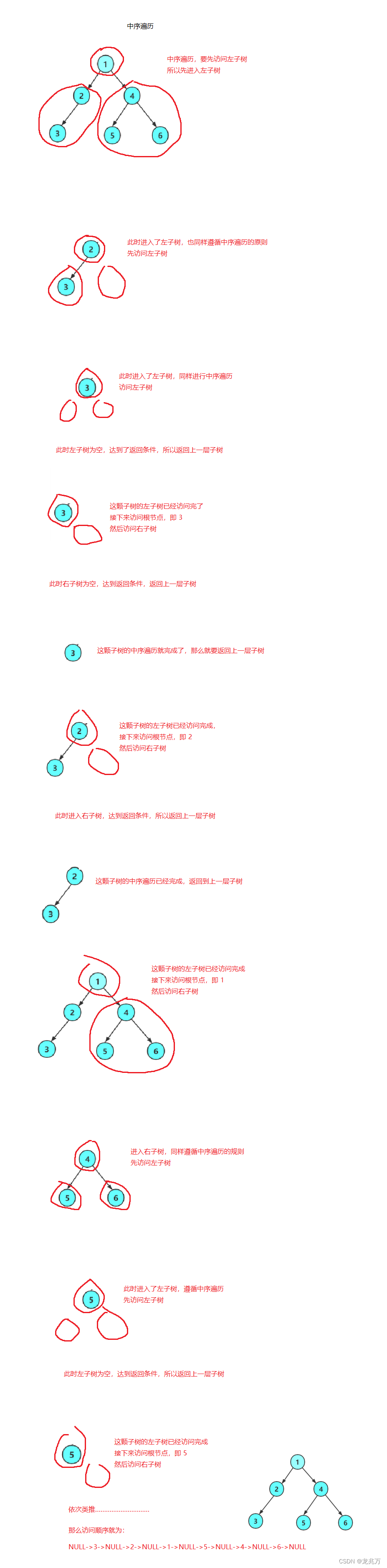
那么现在我们不写代码，来单独分析各个遍历顺序依次访问到谁：

前序遍历：

中序遍历：

后序遍历：

上面的图就是建立在递归思想上得来的，或许逻辑有些不清晰，但递归思想就是如此。现在我们可以开始着手我们的代码了，那么为了方便，我们手动建立一个和上面的二叉树一样的数据结构，同样的，也不使用多文件了。

#include <assert.h>
#include <stdlib.h>

typedef int BinaryData;
typedef struct Node
{
    BinaryData* a;
    struct Node* left;
    struct Node* right;
}Node;

Node* NodeInit()
{
    Node* n1 = (Node*)malloc(sizeof(Node));
    assert(n1);
    Node* n2 = (Node*)malloc(sizeof(Node));
    assert(n2);
    Node* n3 = (Node*)malloc(sizeof(Node));
    assert(n3);
    Node* n4 = (Node*)malloc(sizeof(Node));
    assert(n4);
    Node* n5 = (Node*)malloc(sizeof(Node));
    assert(n5);
    Node* n6 = (Node*)malloc(sizeof(Node));
    assert(n6);

    n1 = 1;
    n2 = 2;
    n3 = 3;
    n4 = 4;
    n5 = 5;
    n6 = 6;

    n1->left = n2;
    n1->right = n4;
    n2->left = 3;
    n2->right = NULL;
    n3->left = NULL;
    n3->right = NULL;
    n4->left = n5;
    n4->right = n6;
    n5->left = NULL;
    n5->right = NULL;
    n6->left = NULL;
    n6->right = NULL;

    return n1;
}

int main()
{
    Node* root = NodeInit();
    return 0;
}

//前序遍历
void PreTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%d ", root->val);
    PreTraval(root->left);
    PreTraval(root->right);
}


//中序遍历
void MidTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    MidTraval(root->left);
    printf("%d ", root->val);
    MidTraval(root->right);
}


//后序遍历
void PosTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    PosTraval(root->left);
    PosTraval(root->right);

既然都写到这了，我们不妨来看看怎么求得节点个数。

//节点个数
int count = 0;
int NodeSize(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    count++;
    NodeSize(root->left);
    NodeSize(root->right);
    return count;
}

我们看到，我们使用全局变量计数的方法能够设计出代码，但是我们有一个很严重的问题，全局变量它只初始化一次，那么第二次调用这个函数的时候count的值并不为0，所以这个方法是不可取的。即使我们在内部定义static修饰的局部变量，作用还是一样的。

int main()
{
    Node* root = NodeInit();
    //PreTraval(root);
    //MidTraval(root);
    //PosTraval(root);
    
    //当我们二次调用函数时
    printf("NodeSize = %d\n", NodeSize(root));
    printf("NodeSize = %d\n", NodeSize(root));
    return 0;
}

那么我们就要设计递归代码了。

//节点个数
//int count = 0;
//int NodeSize(Node* root)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    count++;
//    NodeSize(root->left);
//    NodeSize(root->right);
//    return count;
//}
int NodeSize(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return NodeSize(root->left) + NodeSize(root->right) + 1;
}

使用同一个主函数打印的结果：

我们再试着求一下叶节点的个数。

//叶节点的个数
int LeafSize(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return LeafSize(root->left) + LeafSize(root->right);
}

我们再设计求出第k层的节点个数的代码。

//第k层的节点个数
int K_NodeSize(Node* root, int k)
{
    assert(k > 0);
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return K_NodeSize(root->left, k - 1) + K_NodeSize(root->right, k - 1);
}

假设我们求的是第2层的节点个数。

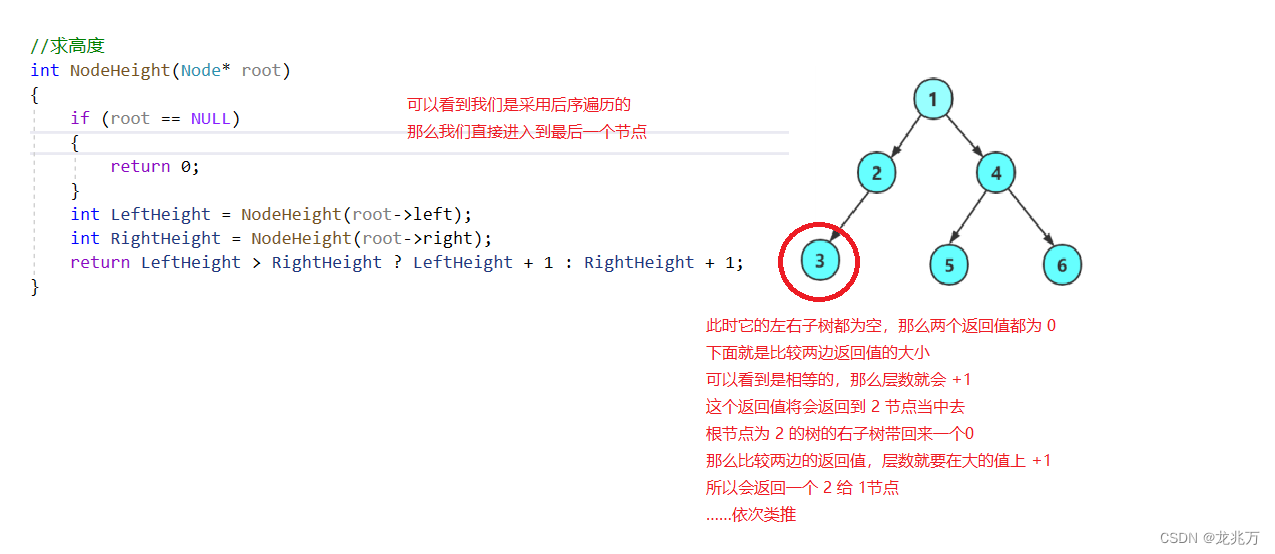
最后我们设计一个函数，这个函数能够求二叉树的高度。

//求高度
int NodeHeight(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    int LeftHeight = NodeHeight(root->left);
    int RightHeight = NodeHeight(root->right);
    return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}

那么我我们可以通过画图的形式来捋清楚这个思路：

完整代码：

#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
typedef int BinaryData;
typedef struct Node
{
    BinaryData val;
    struct Node* left;
    struct Node* right;
}Node;

Node* NodeInit()
{
    Node* n1 = (Node*)malloc(sizeof(Node));
    assert(n1);
    Node* n2 = (Node*)malloc(sizeof(Node));
    assert(n2);
    Node* n3 = (Node*)malloc(sizeof(Node));
    assert(n3);
    Node* n4 = (Node*)malloc(sizeof(Node));
    assert(n4);
    Node* n5 = (Node*)malloc(sizeof(Node));
    assert(n5);
    Node* n6 = (Node*)malloc(sizeof(Node));
    assert(n6);

    n1->val = 1;
    n2->val = 2;
    n3->val = 3;
    n4->val = 4;
    n5->val = 5;
    n6->val = 6;

    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n2->right = NULL;
    n3->left = NULL;
    n3->right = NULL;
    n4->left = n5;
    n4->right = n6;
    n5->left = NULL;
    n5->right = NULL;
    n6->left = NULL;
    n6->right = NULL;

    return n1;
}

//前序遍历
void PreTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%d ", root->val);
    PreTraval(root->left);
    PreTraval(root->right);
}

//中序遍历
void MidTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    MidTraval(root->left);
    printf("%d ", root->val);
    MidTraval(root->right);
}

//后序遍历
void PosTraval(Node* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    PosTraval(root->left);
    PosTraval(root->right);
    printf("%d ", root->val);
}

//节点个数
//int count = 0;
//int NodeSize(Node* root)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    count++;
//    NodeSize(root->left);
//    NodeSize(root->right);
//    return count;
//}
int NodeSize(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return NodeSize(root->left) + NodeSize(root->right) + 1;
}

//叶节点的个数
int LeafSize(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return LeafSize(root->left) + LeafSize(root->right);
}

//第k层的节点个数
int K_NodeSize(Node* root, int k)
{
    assert(k > 0);
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return K_NodeSize(root->left, k - 1) + K_NodeSize(root->right, k - 1);
}

//求高度
int NodeHeight(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }
    int LeftHeight = NodeHeight(root->left);
    int RightHeight = NodeHeight(root->right);
    return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
int main()
{
    Node* root = NodeInit();
    //PreTraval(root);
    //MidTraval(root);
    //PosTraval(root);
    
    //当我们二次调用函数时
    //printf("NodeSize = %d\n", NodeSize(root));
    //printf("NodeSize = %d\n", NodeSize(root));

    //printf("LeafSize = %d\n", LeafSize(root));
    //printf("K_NodeSize = %d\n", K_NodeSize(root, 2));
    
    printf("NodeHeight = %d\n", NodeHeight(root));
    return 0;
}

本篇的二叉树介绍就到这里，后续的内容我会马上整理出来。

标签： 数据结构
本文转载自: https://blog.csdn.net/weixin_59913110/article/details/126531789
版权归原作者 龙兆万 所有， 如有侵权，请联系我们删除。
登录后发布评论

“C语言描述数据结构 &mdash;&mdash; 二叉树(3)前、中、后序遍历”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

机器人技术在安全领域的重要作用

安全学习记录——网络篇（一）

图腾柱PFC：HP1010为您的电动两轮车之旅提供绿色，高效，安全的动力

单元测试数据库回滚问题

这才是单元测试，之前我们都错了

【C语言基础】：字符函数和字符串函数

ChatGPT-Next-Web SSRF漏洞+XSS漏洞复现(CVE-2023-49785)

文章导航