使用阈值调优改进分类模型性能

阈值调优是数据科学中一个重要且必要的步骤。它与应用程序领域密切相关，并且需要一些领域内的知识作为参考。在本文中将演示如何通过阈值调优来提高模型的性能。

用于分类的常用指标

一般情况下我们都会使用准确率accuracy来评价分类的性能，但是有很多情况下accuracy 不足以报告分类模型的性能，所以就出现了很多其他的指标：精确度Precision、召回率Recall、F1 分数F1 score和特异性Specificity。除此以外，还有 ROC 曲线、ROC AUC 和 Precision-Recall 曲线等等。

让我们首先简单解释这些指标和曲线的含义：

精确度Precision：所有正例中真正正例的数量。P=TP/(TP+FP)

召回率Recall：正例数超过真正例数加上假负例数。R=TP/(TP+FN)

F1 分数F1 score：Precision 和 Recall 之间的调和平均值。

特异性Specificity：真负例的数量超过真负例的数量加上假正例的数量。Spec=TN(TN+FP)

(ROC) 曲线：该曲线显示了真正例率和假正例率之间的权衡。代表模型的性能。

ROC曲线下面积（AUC）：ROC曲线下面积。如果这个面积等于 1，我们就有了一个完美的分类器。如果它等于 0.5，那么就是一个随机的分类器。

Precision-Recall曲线：这条曲线显示了不同阈值下的精度和召回值。它用于可视化 Precision 和 Recall 之间的权衡。

一般来说，我们必须考虑所有这些指标和曲线。为了将这些内容显示在一起查看，这里定义了一个方法：

 def make_classification_score(y_test, predictions, modelName):
     tn, fp, fn, tp = confusion_matrix(y_test, predictions).ravel() # ravel() used to convert to a 1-D array
     prec=precision_score(y_test, predictions)
     rec=recall_score(y_test, predictions)
     f1=f1_score(y_test, predictions)
     acc=accuracy_score(y_test, predictions)
     # specificity
     spec=tn/(tn+fp)
 
     score = {'Model': [modelName], 'Accuracy': [acc], 'f1': [f1], 'Recall': [rec], 'Precision': [prec], \
         'Specificity': [spec], 'TP': [tp], 'TN': [tn], 'FP': [fp], 'FN': [fn], 'y_test size': [len(y_test)]}
     df_score = pd.DataFrame(data=score)
     return df_score

“预测概率”技巧

当我们测试和评估模型时，将预测的 Y 与测试集中的 Y 进行比较。但是这里不建议使用 model.predict(X_test) 方法，直接返回每个实例的标签，而是直接返回每个分类的概率。例如sklearn 提供的 model.predict_proba(X_test) 的方法来预测类概率。然后我们就可以编写一个方法，根据决策阈值参数返回每个实例的最终标签。

 def probs_to_prediction(probs, threshold):
     pred=[]
     for x in probs[:,1]:
         if x>threshold:
             pred.append(1)
         else:
             pred.append(0)
     return pred

如果设置thresh = 0.5 那么则和调用 model.predict(X_test) 方法得到的结果是相同的，但是使用概率我们可以测试不同的阈值的性能表现。

如果改变阈值则会改变模型的性能。这里可以根据应用程序领域选择一个阈值来最大化重要的度量(通常是精度或召回率)，比如在kaggle的比赛中经常会出现thresh = 0.4xx的情况。

选择重要的度量

最大化的重要指标是什么呢?如何确定?

在二元分类任务中，我们的模型会出现两种类型的错误:

第一类错误:预测Y为True，但它实际上是False。也称为假正例错误。

第二类错误:预测Y为False，但它实际上是True。也称为假负例错误。

错误分类实例的数量决定了模型的好坏。但这些错误并不同等重要，对于不用的领域有着不同的要求，比如医学的检测和金融的风控中，需要尽量减小假负例也就是避免第二类错误，需要最小化假负例的数量，那么最大化的重要指标是召回率。

同理,如果要避免第一类错误，我们需要最小化假正例的数量，所以最大化的重要指标是精度。

为了最大化指标，我们可以移动阈值，直到我们在所有指标之间达成良好的平衡，这时就可以使用Precision-Recall曲线，当然也可以使用ROC曲线。

但是要说明的是，我们不能最大化所有指标，因为通过指标的定义就能看到这是不可能的。

阈值优化

假设我们正在处理一个二元分类任务的逻辑回归模型。我们已经进行了训练、超参数调优和测试阶段。该模型已经过交叉验证。也就是说，基本上能做的事情我们都已经做了，但是还是希望能够有一些其他的方式来优化模型，那么则可以试试调整模型的阈值。

对于sklearn来说使用model.predict_proba(X_test)方法来获得类概率，如果使用神经网络的化一般都会输出的是每个类的概率，所以我们这里以sklearn为例，使用这个概率值:

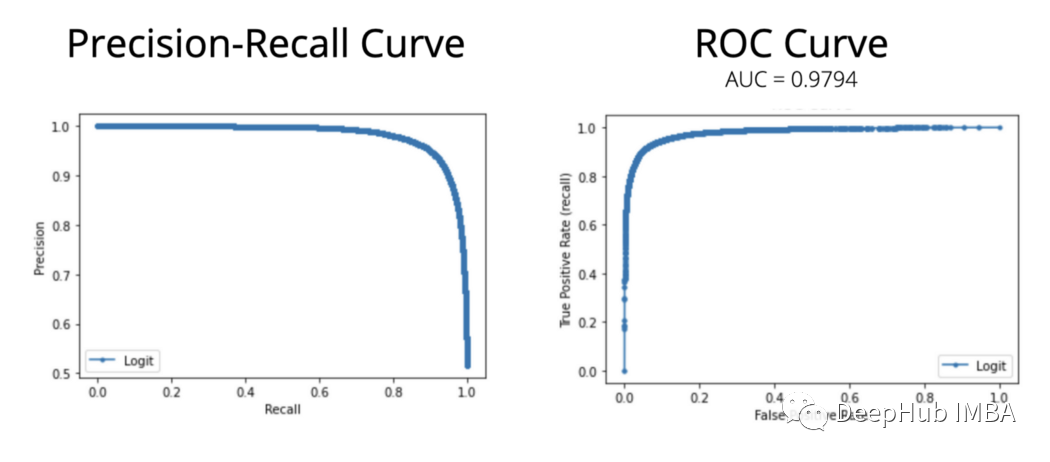
• 计算ROC AUC，它等于0.9794
• 计算并绘制ROC曲线
• 计算并绘制精度-召回率曲线

下面的代码块表示这些步骤:

 def probs_to_prediction(probs, threshold):
     pred=[]
     for x in probs[:,1]:
         if x>threshold:
             pred.append(1)
         else:
             pred.append(0)
     return pred
 
 # getting predicted probability values
 probability = model.predict_proba(X_test)
 
 # calculate ROC AUC score. AUC = 0.9794
 print("Logit: ROC AUC = %.4f" % roc_auc_score(y_test, probability[:, 1]))
 
 # calculate and plot the ROC curve
 model_fpr, model_tpr, _ = roc_curve(y_test, probability[:, 1])
 plt.plot(model_fpr, model_tpr, marker='.', label='Logit')
 plt.xlabel('False Positive Rate')
 plt.ylabel('True Positive Rate (recall)')
 plt.legend()
 plt.title("ROC Curve")
 plt.show()
 
 # calculate and plot the Precision-Recall curve
 model_precision, model_recall, thresholds = precision_recall_curve(y_test, probability[:, 1])
 plt.plot(model_recall, model_precision, marker='.', label='Logit')
 plt.xlabel('Recall')
 plt.ylabel('Precision')
 plt.legend()
 plt.title('Precision-Recall Curve')
 plt.show()

下图的曲线。可以看到模型的性能很好。

在本例中，假设在我们的实际应用中FP的成本> FN的成本，所以选择一个阈值在不降低召回率的情况下最大化精度。使用Precision-Recall曲线来对一个可能的阈值进行初始选择。在下面的代码中，绘制了带有候选阈值的Precision-Recall曲线。

 plt.plot(model_recall, model_precision, marker='.', label='Logit')
 plt.plot(model_recall[43000], model_precision[43000], "ro", label="threshold")
 plt.xlabel('Recall')
 plt.ylabel('Precision')
 plt.legend()
 plt.title('Precision and Recall values for a chosen Threshold')
 plt.show()

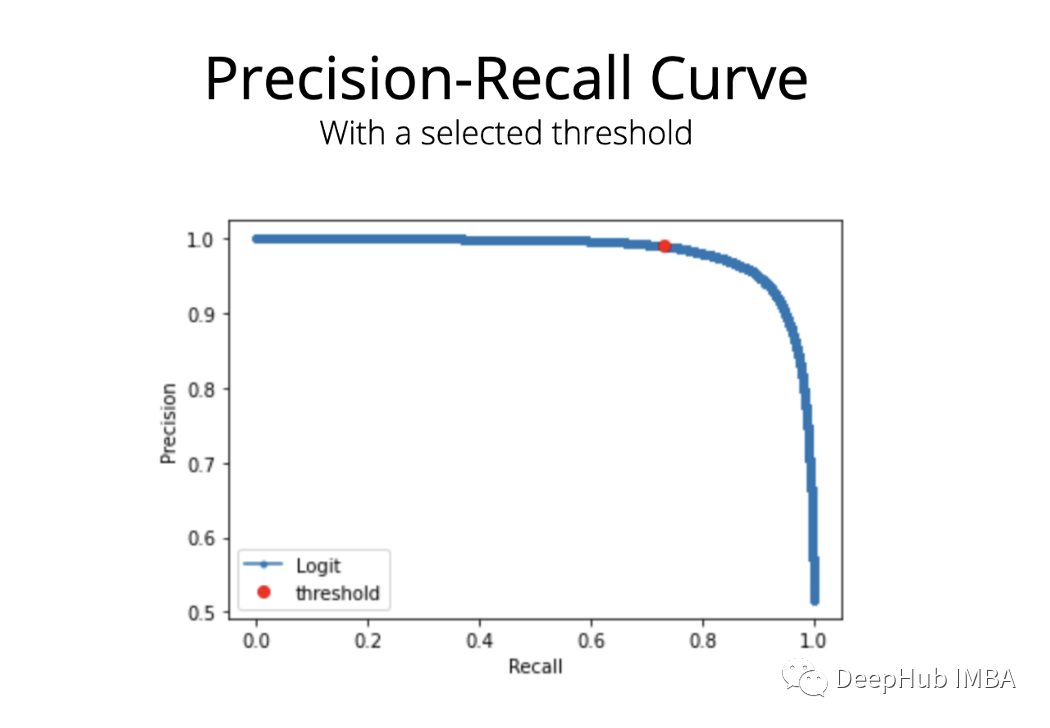
这样就可以使用选定的阈值来获得最终的分类标签并计算性能指标。并且可以多次进行选择不同阈值进行对比。

 print("Threshold value = %.4f" % thresholds[43000])
 
 # results with the chosen threshold
 predictions = probs_to_prediction(probability, thresholds[43000])
 make_classification_score(y_test, predictions, "logit, custom t")

下图中可以看到，所选的阈值以召回率为代价来最大化精度。根据我们应用的决策阈值，相同的模型可以表现出一些不同的性能。

通过调整阈值并进行结果的对比，一旦对结果满意，模型就可以投入到生产中了。

总结

为分类模型选择最重要的评价指标并不容易。这种选择通常与应用程序领域有关，必须考虑错误分类的代价。在某些情况下，可能有必要咨询领域专家确定哪些错误代表最大的风险。

模型的行为很大程度上受到阈值选择的影响，我们可以应用不同的技术来评估模型并调优阈值以获得预期的结果。

作者：Edoardo Bianchi