目录
0 写在前面
机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。
🚀详情：机器学习强基计划(附几十种经典模型源码合集)
本期目标：实现这样一个效果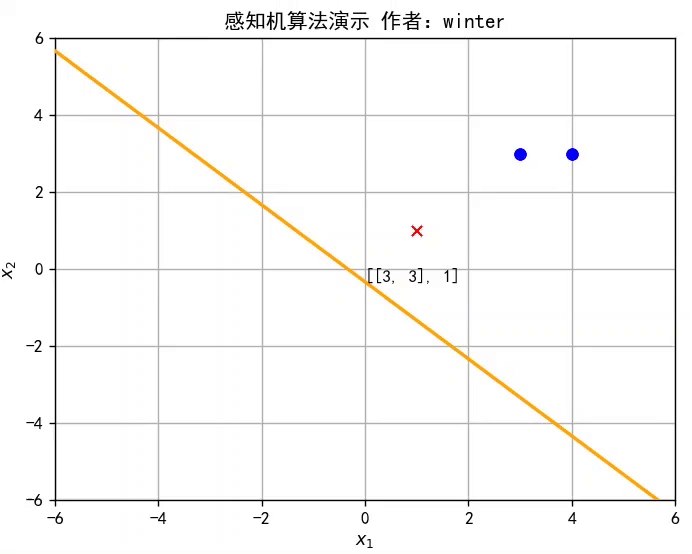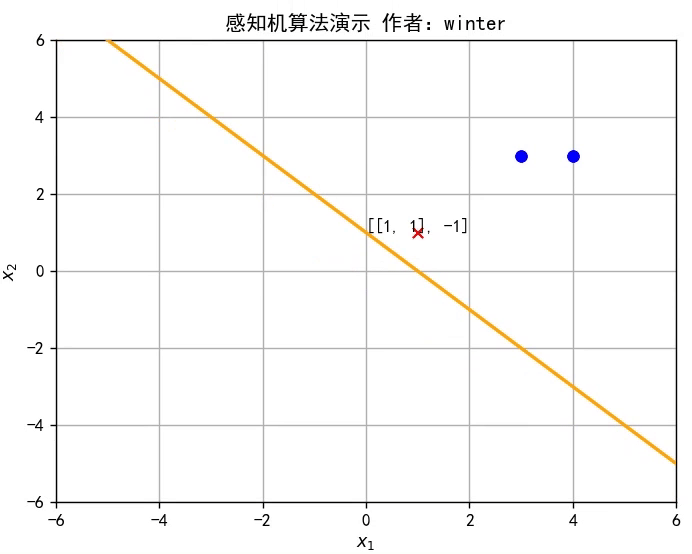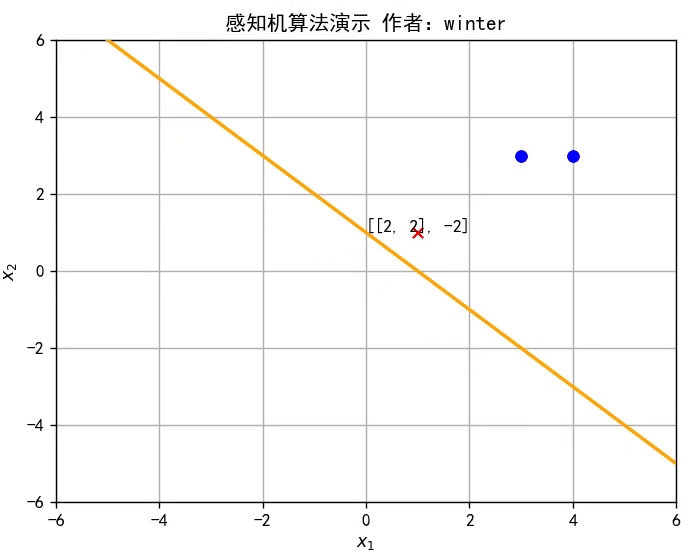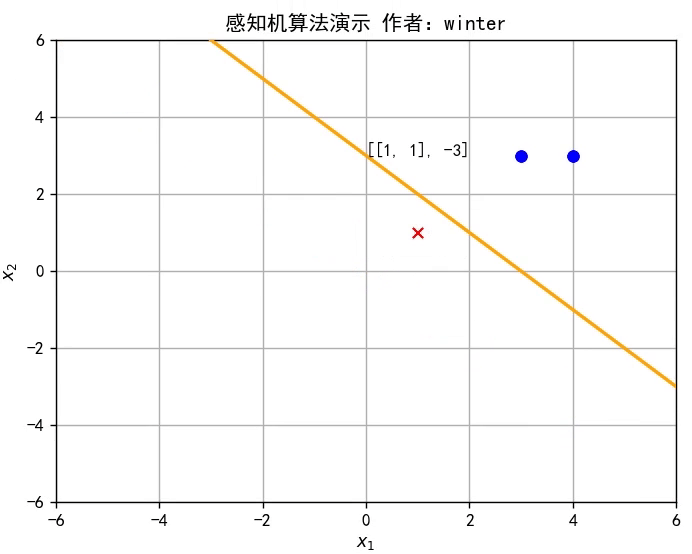
1 什么是线性模型？
线性模型的假设形式是属性权重、偏置与属性的线性组合，即
f
(
x
(
i
)
)
=
w
T
x
(
i
)
+
b
f\left( \boldsymbol{x}^{\left( i \right)} \right) =\boldsymbol{w}^T\boldsymbol{x}^{\left( i \right)}+b
f(x(i))=wTx(i)+b
其中
x
(
i
)
=
[
x
1
(
i
)
x
2
(
i
)
⋯
x
d
(
i
)
]
T
\boldsymbol{x}^{\left( i \right)}=\left[ \begin{matrix} x_{1}^{\left( i \right)}& x_{2}^{\left( i \right)}& \cdots& x_{d}^{\left( i \right)}\\\end{matrix} \right] ^T
x(i)=[x1(i)x2(i)⋯xd(i)]T是数据集
D
D
D中的第
i
i
i个样本，
x
j
(
i
)
(
j
=
1
,
2
,
⋯
,
d
)
x_{j}^{\left( i \right)}\left( j=1, 2, \cdots , d \right)
xj(i)(j=1,2,⋯,d)是该数据集样本的
d
d
d个属性；
w
=
[
w
1
w
2
⋯
w
d
]
T
\boldsymbol{w}=\left[ \begin{matrix} \boldsymbol{w}_1& \boldsymbol{w}_2& \cdots& \boldsymbol{w}_d\\\end{matrix} \right] ^T
w=[w1w2⋯wd]T是样本属性的权重向量；
b
b
b是模型偏置。
上式也可写为齐次形式
f
(
x
(
i
)
)
=
w
^
T
[
x
(
i
)
1
]
f\left( \boldsymbol{x}^{\left( i \right)} \right) =\boldsymbol{\hat{w}}^T\left[ \begin{array}{c} \boldsymbol{x}^{\left( i \right)}\\ 1\\\end{array} \right]
f(x(i))=w^T[x(i)1]
其中系数向量
w
^
=
[
w
;
b
]
\boldsymbol{\hat{w}}=\left[ \boldsymbol{w}; b \right]
w^=[w;b]
进一步，考虑单调可微函数
g
(
⋅
)
g\left( \cdot \right)
g(⋅)，令
f
(
x
(
i
)
)
=
g
−
1
(
w
T
x
(
i
)
+
b
)
f\left( \boldsymbol{x}^{\left( i \right)} \right) =g^{-1}\left( \boldsymbol{w}^T\boldsymbol{x}^{\left( i \right)}+b \right)
f(x(i))=g−1(wTx(i)+b)
称为**广义线性模型(generalized linear model)**，其中
g
(
⋅
)
g\left( \cdot \right)
g(⋅)称为**联系函数(link function)**。
广义线性模型本质上仍是线性的，但通过
g
(
⋅
)
g\left( \cdot \right)
g(⋅)进行非线性映射，使之具有更强的拟合能力，类似神经元的激活函数。例如**对数线性回归(log-linear regression)**是
g
(
⋅
)
=
ln
(
⋅
)
g\left( \cdot \right) =\ln \left( \cdot \right)
g(⋅)=ln(⋅)时的情形，此时模型拥有了指数逼近的性质。
线性模型的优点是形式简单、易于建模、可解释性强，是更复杂非线性模型的基础。
2 感知机概述
**感知机(Perceptron)**是最简单的二分类线性模型，也是神经网络的起源算法，如图所示。
y
=
w
^
T
x
^
y=\boldsymbol{\hat{w}}^{\boldsymbol{T}}\boldsymbol{\hat{x}}
y=w^Tx^是
R
d
\mathbb{R} ^d
Rd空间的一条直线，因此**感知机实质上是通过训练参数
w
^
\boldsymbol{\hat{w}}
w^改变直线位置，直至将训练集分类完全**，如图所示，或者参考文章开头的动图。
3 手推感知机原理
机器学习强基计划的初衷就是搞清楚每个算法、每个模型的数学原理，让我们开始吧！
感知机的损失函数定义为全体误分类点到感知机切割超平面的距离之和：
E
(
w
^
)
=
1
∥
w
^
∥
∑
i
=
1
n
∣
w
^
T
x
^
e
r
r
o
r
(
i
)
∣
E\left( \boldsymbol{\hat{w}} \right) =\frac{1}{\left\| \boldsymbol{\hat{w}} \right\|}\sum_{i=1}^n{\left| \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)} \right|}
E(w^)=∥w^∥1i=1∑n∣∣w^Tx^error(i)∣∣
对于二分类问题
y
∈
{
−
1
,
1
}
y\in \left\{ -1, 1 \right\}
y∈{−1,1}，则误分类点的判断方法为
−
y
i
w
^
T
x
^
e
r
r
o
r
(
i
)
>
0
-y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}>0
−yiw^Tx^error(i)>0
- 假如 y i = − 1 y_i=-1 yi=−1为反例，但是误判为正例(样本点在直线上方)，则 w ^ T x ^ e r r o r ( i ) > 0 \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}{error}^{\left( i \right)}>0 w^Tx^error(i)>0，所以 − y i w ^ T x ^ e r r o r ( i ) > 0 -y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}{error}^{\left( i \right)}>0 −yiw^Tx^error(i)>0
- 假如 y i = 1 y_i=1 yi=1为正例，但是误判为反例(样本点在直线下方)，则 w ^ T x ^ e r r o r ( i ) < 0 \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}{error}^{\left( i \right)}<0 w^Tx^error(i)<0，所以 − y i w ^ T x ^ e r r o r ( i ) > 0 -y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}{error}^{\left( i \right)}>0 −yiw^Tx^error(i)>0
这在二分类问题中是个很常用的技巧，后面还会遇到这种等效形式。
从而损失函数也可简化为下面的形式以便于求导：
E
(
w
^
)
=
−
∑
i
=
1
n
y
i
w
^
T
x
^
e
r
r
o
r
(
i
)
E\left( \boldsymbol{\hat{w}} \right) =-\sum_{i=1}^n{y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}_{error}^{\left( i \right)}}
E(w^)=−i=1∑nyiw^Tx^error(i)
这里省略了
1
∥
w
^
∥
\frac{1}{\left\| \boldsymbol{\hat{w}} \right\|}
∥w^∥1是因为直线
w
^
T
x
^
=
0
\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}=0
w^Tx^=0
方程两边同时乘以系数都成立，所以直线系数
w
^
\boldsymbol{\hat{w}}
w^可以随意缩放，这里可令
∥
w
^
∥
=
1
\left\| \boldsymbol{\hat{w}} \right\|=1
∥w^∥=1
若采用梯度下降法进行优化(梯度法可参考图文详解神秘的梯度下降算法原理(附Python代码))，则算法流程为：
- 初始化 w ^ 0 \boldsymbol{\hat{w}}_0 w^0；
- 在训练集中任意选取点 x ( i ) \boldsymbol{x}^{\left( i \right)} x(i)；
- 判断 x ( i ) \boldsymbol{x}^{\left( i \right)} x(i)是否可被当前感知机正确分类，若可以则转至第二步直至没有误分类点，否则执行梯度优化进行参数更新： w ^ ∗ = w ^ + γ y ( i ) x ( i ) \boldsymbol{\hat{w}}^*=\boldsymbol{\hat{w}}+\gamma y^{\left( i \right)}\boldsymbol{x}^{\left( i \right)} w^∗=w^+γy(i)x(i)。
4 Python实现
4.1 创建感知机类
classPerceptron:def__init__(self):
self.w = np.mat([0,0])# 初始化权重
self.b =0# 初始化偏置
self.delta =1# 设置学习率为1
self.train_set =[[np.mat([3,3]),1],[np.mat([4,3]),1],[np.mat([1,1]),-1]]# 设置训练集
self.history =[]# 训练历史
4.2 更新权重与偏置
defupdate(self,error_point):
self.w += self.delta*error_point[1]*error_point[0]
self.b += self.delta*error_point[1]
self.history.append([self.w.tolist()[0],self.b])
4.3 判断误分类点
defjudge(self,point):return point[1]*(self.w*point[0].T+self.b)
4.4 训练感知机
deftrain(self):
flag =Truewhile(flag):
count =0for point in self.train_set:if(self.judge(point)<=0):
self.update(point)else:
count +=1if(count ==len(self.train_set)):
flag =False
4.5 动图可视化
defshow():print("参数w,b更新过程：",perceptron.history)
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(perceptron.history),
interval=1000, repeat=False,blit=True)
plt.show()
限于篇幅，完整代码可以通过下方名片联系我获取
5 总结
感知机最大的缺陷在于其线性，单个感知机只能表达一条直线，即使是如图(a)所示简单的异或门样本，都无法进行分类。对此有两种解决方式：
- 通过多条直线，即**多层感知机(Multi-Layer Perceptron, MLP)**进行分类，如图(b)所示；
- 在线性加权的基础上引入非线性变换，如图(c)所示。
🔥 更多精彩专栏：
- 《ROS从入门到精通》
- 《机器人原理与技术》
- 《机器学习强基计划》
- 《计算机视觉教程》
- …
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
本文转载自: https://blog.csdn.net/FRIGIDWINTER/article/details/126131955
版权归原作者 Mr.Winter` 所有， 如有侵权，请联系我们删除。
版权归原作者 Mr.Winter` 所有， 如有侵权，请联系我们删除。