数据结构-01-串，KMP模式匹配

数据结构-01-串，KMP模式匹配

1.1 聊聊串这种数据结构

串，即字符串，是由零个或多个字符组成的有限序列，通常由单引号或双引号括起来。例如 S=‘Hello World’ 就是一个字符串，S是串名，单引号括起来的字符是串的值（单引号不属于串的内容）。
几个关于串的术语：
1，子串：串中任意个连续字符组成的子序列，例如一个串S=‘Hello World’ ，T=‘orl’，则称T是S的一个子串。
2，主串：包含子串的串，上面S也可称为子串T的主串。
3，字符在主串中的位置：字符在串中第一次出现的位置，串S同上，则字符 ‘l’ 在串S中的位置为3。
4，子串在主串中的位置：子串中第一个字符在主串中的位置，子串T在主串S中的位置为8。
几个容易忽略的问题：
1，空格也是一种字符，空格串不等于空串。
2，谈到字符串的位序问题时，应该从1开始而不是0。
3，串也是一种特殊的线性表，数据元素之间呈线性关系，但线性表中的数据元素可以各种各样的数据类型，而串中的数据元素必须是字符集。
4，串的增删改查操作通常以子串为操作对象。

1.2 串的常用操作

详细见代码注释

#include<iostream>#include<string.h>usingnamespace std;voidStrAssign(string &str,string T){//赋值操作,将字符串T的值赋给str
    str=T;}voidStrCopy(string str,string &T){//复制操作,将字符串str复制给T
    T=str;}boolstrEmpty(string str){//判空操作,如果字符串str为空串返回True,否则返回Falseif(str.length()==0)returntrue;elsereturnfalse;}intstrLength(string str){//求串长,返回字符串长度return str.length();}voidclearStr(string &str){//清空串
    str="";}voidDestroystr(string &str){//销毁串,回收串的存储空间string().swap(str);}voidconcat(string &str,string a,string b){//串联串,返回由a,b拼接成的字符串
    str=a+b;}

string substr(string str,int i,int j){//返回主串中序列在i与j之间的子串
    string newstr;if(i<=0||j>str.length()||j<i)return"error";for(int t=i-1;t<j;t++) newstr=newstr+str[t];return newstr;}intindex(string s,string t){//求子串t在主串s中的位置int i=0,j=0;while(i<s.length()&&j<t.length()){if(s[i]==t[j]){
            i++;
            j++;}else{
            i=i-j+2;
            j=0;}}if(j==t.length())return i-t.length();elsereturn0;}intmain(){//一个简单调用的例子
    string str,str1;StrAssign(str,"Hello World");//将字符串str赋值为"Hello World"StrCopy(str,str1);//将str的值复制给str1concat(str,str,",I love you");//串联str,",I love you"的值并赋值给str
    cout<<"赋值后str值为:"<<str<<endl;
    cout<<"子串love在主串中的位置为:"<<index(str,"love")<<endl;return0;}

1.3 朴素模式匹配算法

朴素模式匹配算法使用暴力求解，子串和主串分别设置两个指针位于起始位置，两个指针对应字符相比较，如果相等，则两个指针均向前移动一位，若不相等，子串返回起始位置，主串返回原起始位置加一。直至子串或主串指针超过串的长度。若子串指针超过子串的长度则说明在主串中找到了子串，若主串指针超过主串的长度则说明没有找到。
下面看一个例子：在主串S=‘abccbcab’中匹配’cbca’：
起初，主串和匹配串指针分别指向串中第一个元素，分别是a,c，经过比较a与c不相等，匹配串指针继续指向c，主串元素指向第一个元素加一，故指向b。

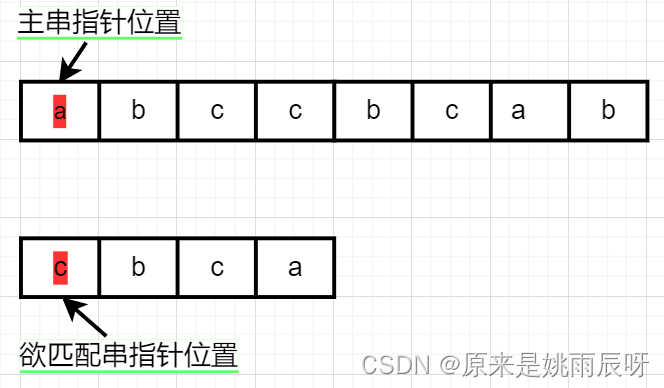
此时比较两个指针元素，一个是b，一个是c仍不相等，故主串指针继续在原起始位置加一，变成c，匹配串指针仍指向c。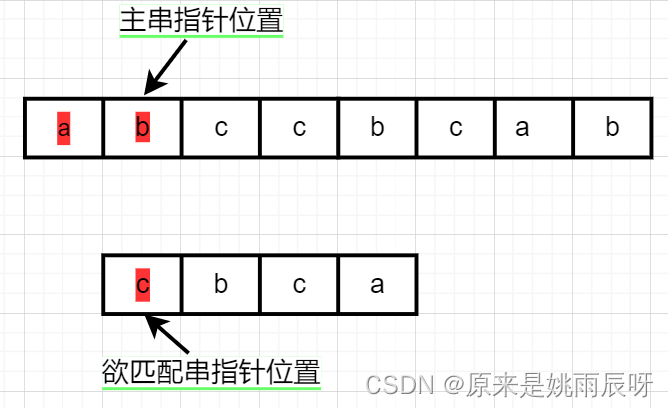

此时两个指针均指向c，相等，两个指针均加一。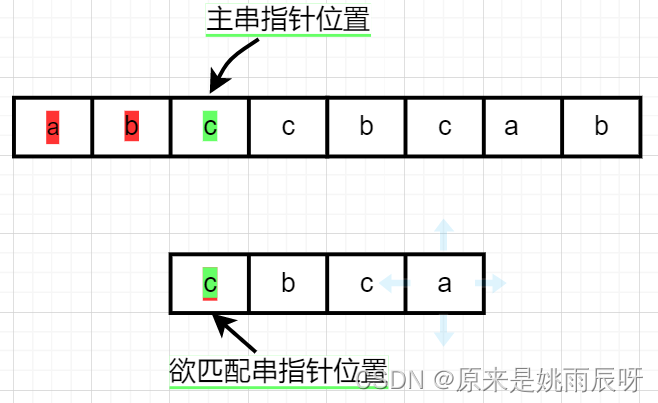

此时主串指针指向c，匹配串指向b，不相等，主串指针指向原起始位置加一，原起始位置是3，故现在指向4，元素对应是c，匹配串指针返回起始位置。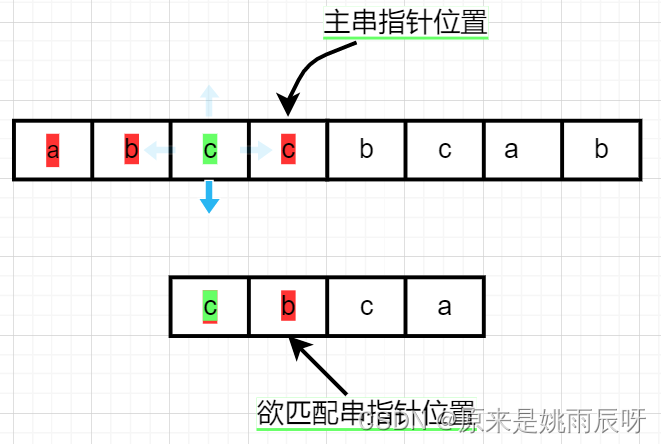

此时两个指针均指向c，相等，两个指针均加一，同理，后三个元素均相等。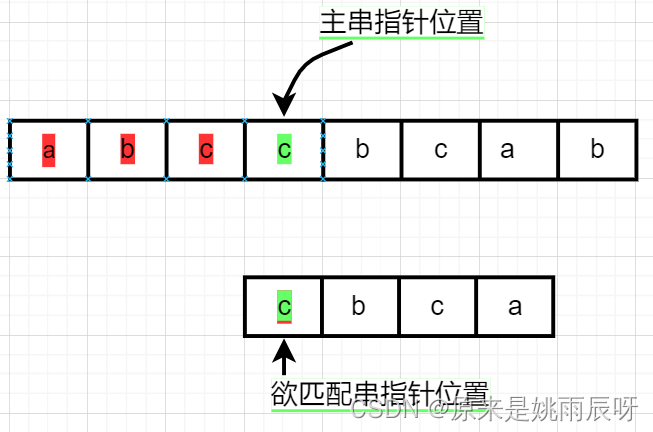

在检查最后一组元素a相等后，主串和匹配串指针均加一，这时匹配串指针将超过匹配串指针长度，程序结束，返回值为主串指针位置-匹配串长度。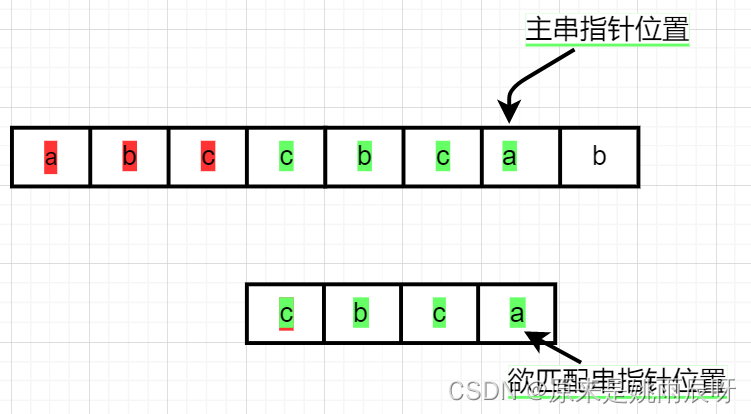

朴素模式匹配的代码实现：

#include<iostream>#include<string.h>usingnamespace std;intindex(string s,string t){//朴素模式匹配int i=0,j=0;while(i<s.length()&&j<t.length()){if(s[i]==t[j]){//若当前指针对应元素相等,则两个指针均加一
            i++;
            j++;}else{
            i=i-j+2;//若对应元素不等,匹配串指针返回起始位置,主串指针返回原起始位置加一
            j=0;}}if(j==t.length())return i-t.length();//若某一指针到达边界值则结束while循环,返回值为主串指针-匹配串长度elsereturn0;}intmain(){//一个简单调用的例子
    cout<<"子串love在主串中的位置为:"<<index("Hello World,I love you","love")<<endl;return0;}

朴素模式匹配时间复杂度分析，及存在的问题：
设主串长度为m，匹配串长度为n，经过上面的分析我们可知，如果匹配串位于主串的末尾，最坏时间复杂度为O(mn)。在算法运行过程中，主串和匹配串的指针均会向前向后徘徊，从而造成了时间的浪费。为了解决以上问题，KMP算法诞生。

1.4 KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。
在深入理解KMP算法之前需要理解几个词语的概念：
1，字符串的前缀：指除字符串中最后一个字符以外，字符串的所有头部子串，如字符串S=‘ababca’，S的前缀为{“a”，“ab”，“aba”，“abab”，“ababc”}
2，字符串的后缀：指除字符串中第一个字符以外，字符串的所有尾部子串，字符串S同上，则S的后缀为{“a”，“ca”，“bca”，“abca”，“babca”}
3，部分匹配值：指字符串前缀后缀相等的最长长度，S同上，S的部分匹配值为1，因为在S的前缀和后缀中有{“a”}等于{“a”}，但{“ab”}不等于{“ca”}。再举一个例子，如T=“aacbcaa”的部分匹配值为2，因为有{“aa”}等于{“aa”}，但{“aac”}不等于{“caa”}。
4，部分匹配值(Partial Match)的表：取字符串中前i个元素(i大于等于1，小于等于字符串长度)，分别求前i个元素组成的子串的部分匹配值，组成的表称为部分匹配值的表。例如：字符串S=‘ababca’，取前i个元素组成的子串为{“a”，“ab”，“aba”，“abab”，“ababc”，“ababca”}，对这些子串分别求部分匹配值为{0，0，1，2，0，1}，故串S部分匹配值的表为：

5，next数组：将上面的部分匹配值表数组中的元素循环右移一位，P[0]处赋值为-1，高位删除，再将所有值加一（这步也可省略，若题目中字符串的标号从0开始则需要加一，如果从1开始则可以省略）。这样的数组就被称为next数组。


上面两个数组均可被称为next数组，区别在于下面的数组所有元素均加了1，这里主要是为了数据的美观和统一，并没有本质上的区别。
KMP算法：我们都知道在朴素模式匹配算法中，当匹配失败时，主串和匹配串指针无脑移动，例如下面这个朴素模式匹配的例子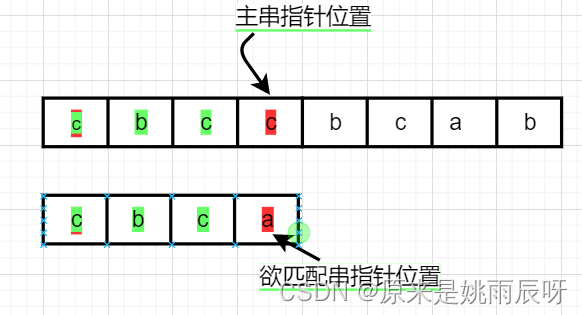

当前三个元素匹配成功后，最后一个元素匹配失败，这时朴素模式匹配的主串指针会重新指向主串第二个元素b，但经过分析我们可知，由于第四个元素匹配失败，主串前三个元素均不可能成功匹配，主串指针原地不动即可。
在KMP算法中next数组就相当于指针的眼睛，当前元素匹配失败时，匹配串指针该移动到哪个位置。举个例子：在S=‘aabbcaababcacabbb’中匹配串“ababca”
第一步，先求匹配串“ababca”的next数组。

第二步，主串和匹配串指针分别位于字符串起始位置开始逐一比较。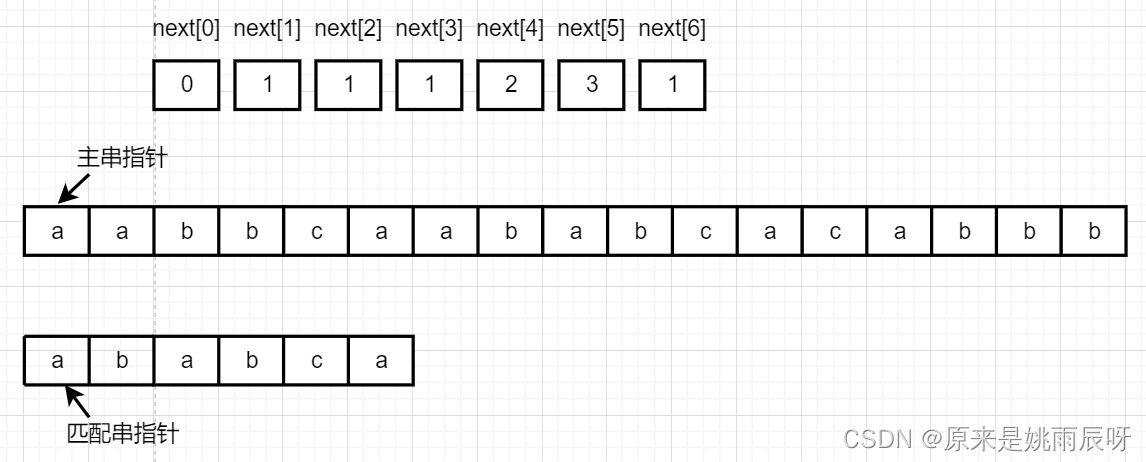

当对应元素相等时，主串指针与匹配串指针均加一。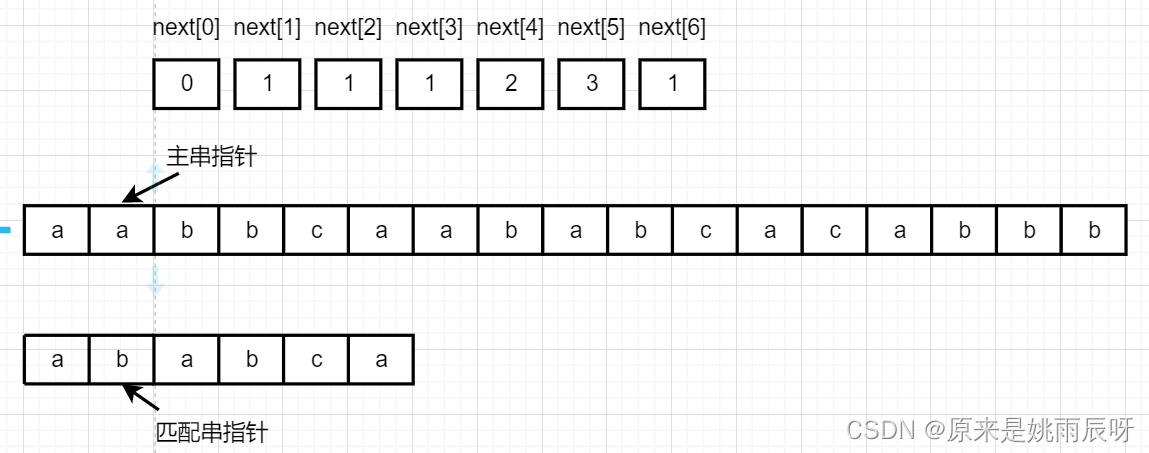

当对应元素不相等时，主串指针不动，匹配串指针指向 next[i] 的位置。next[2]=1，故匹配串指针指向第一个元素。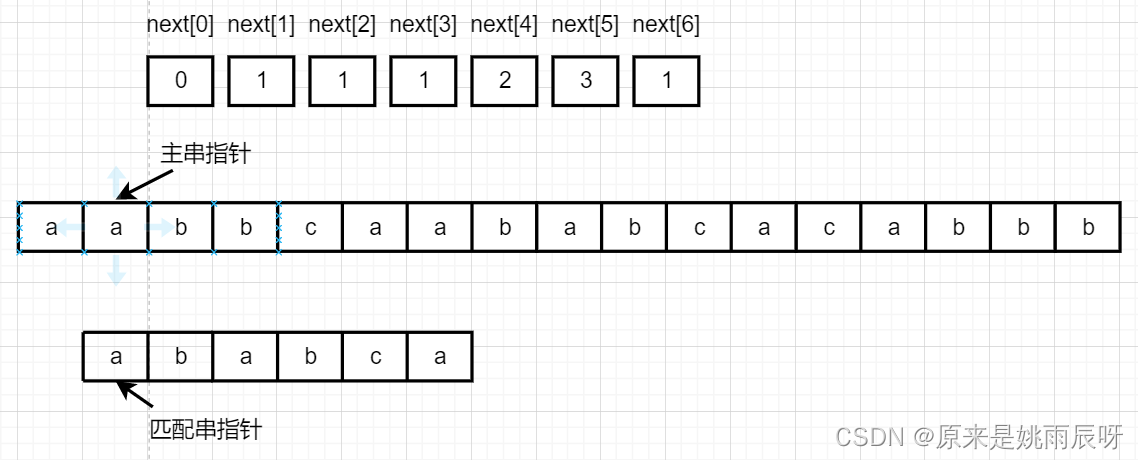

接下来两个元素对应相等，主串和匹配串指针均加一。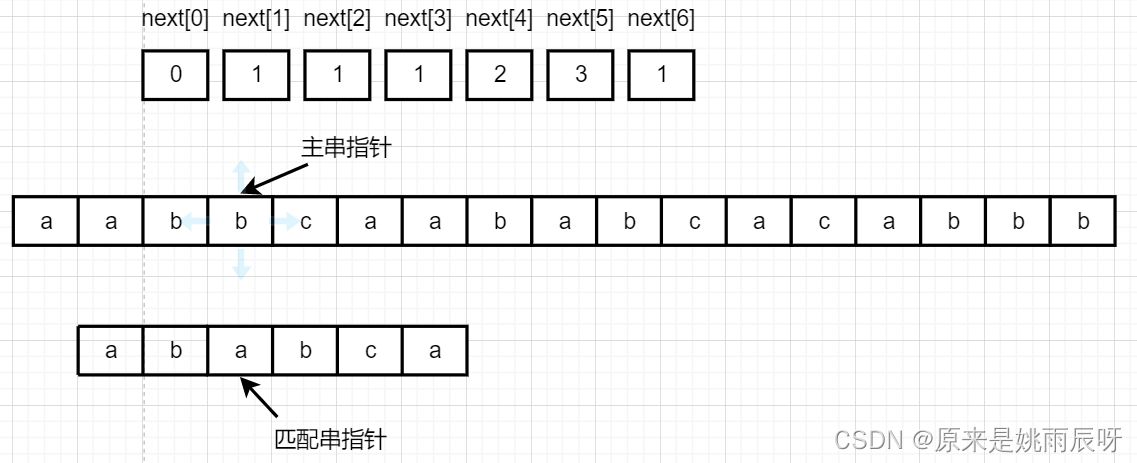

现在对应元素分别为b和a，不相等，主串指针不动，匹配串指针指向next[3]=1。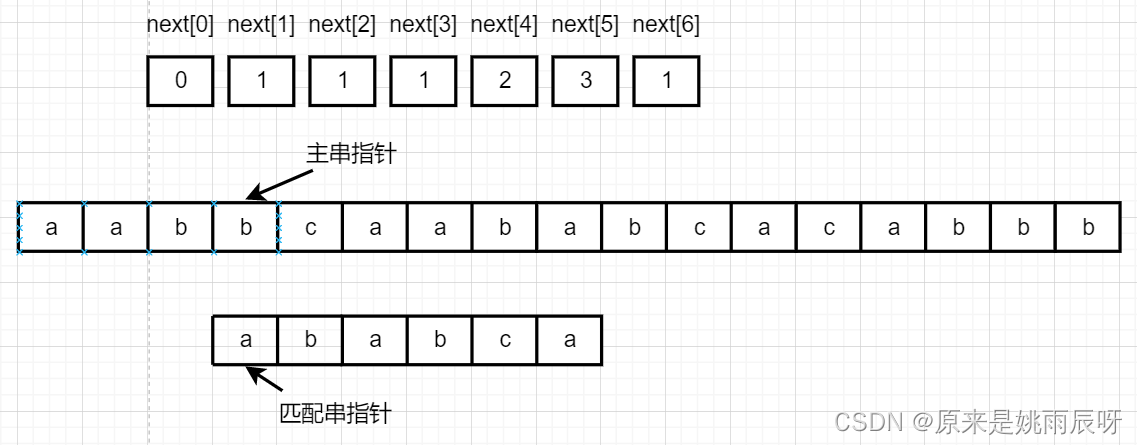

这里对应元素仍是b和a不相等，但由于此时匹配串指针指向第一个元素，故下次匹配时主串指针加一。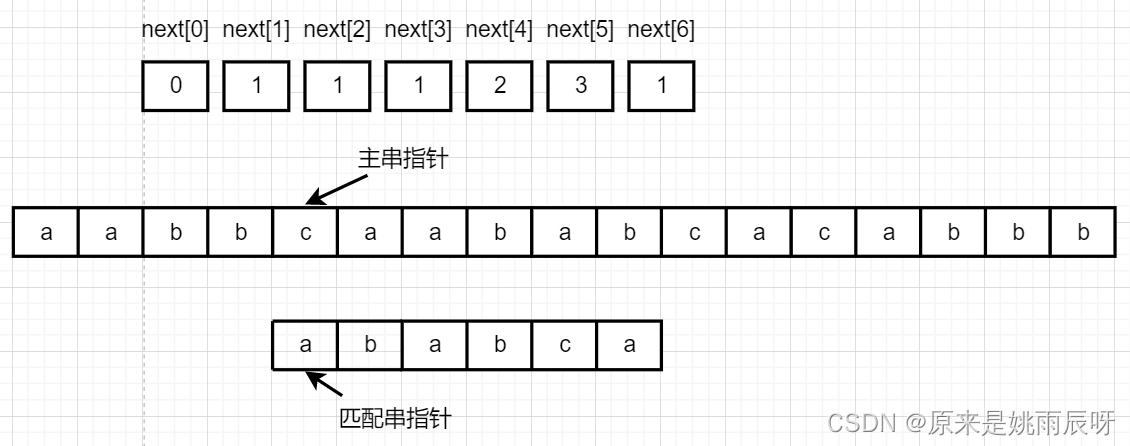

这里对应元素是c和a，仍不相等，同上。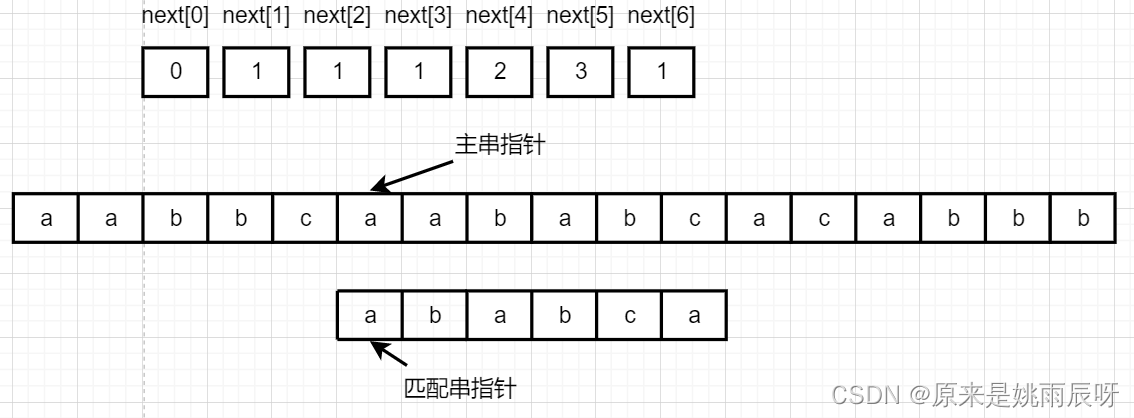

此时a与a相等，主串与匹配串均加一。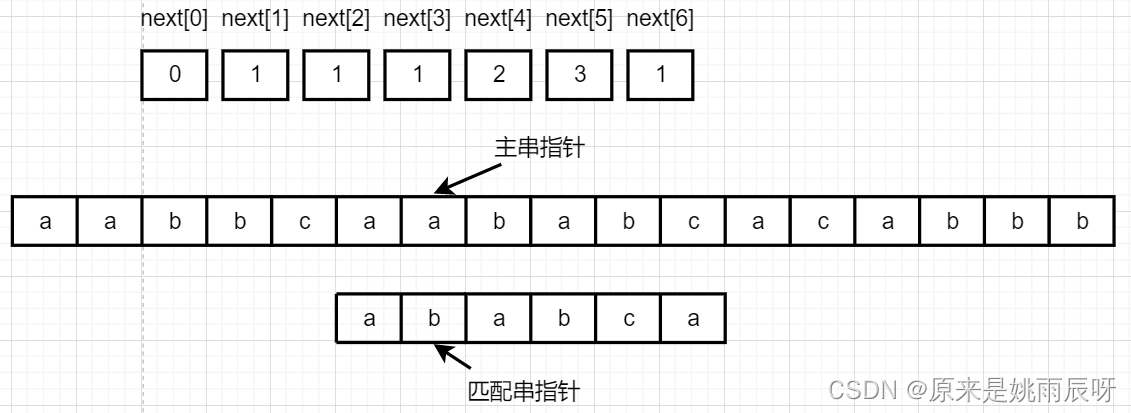

此时a与b不相等，主串指针不动，匹配串指针跳转至next[2]=1处。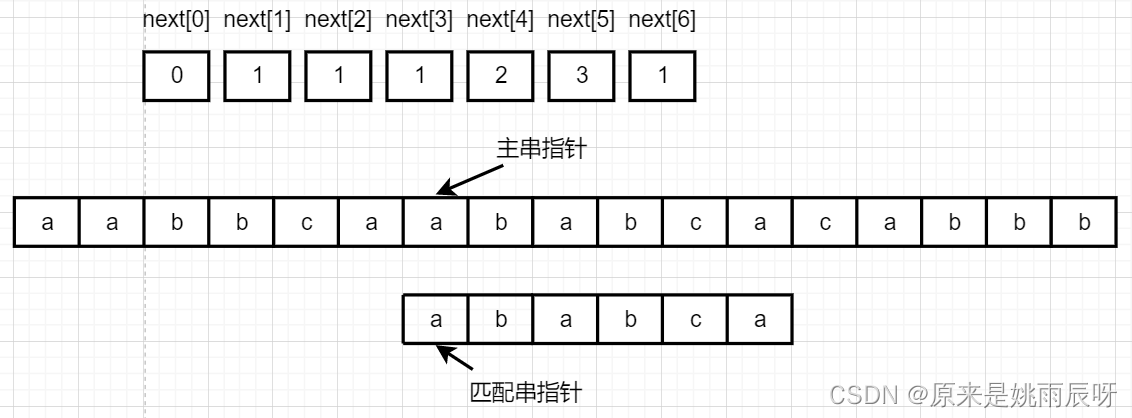

继续匹配，发现对应元素均相等，主串和匹配串指针均加一。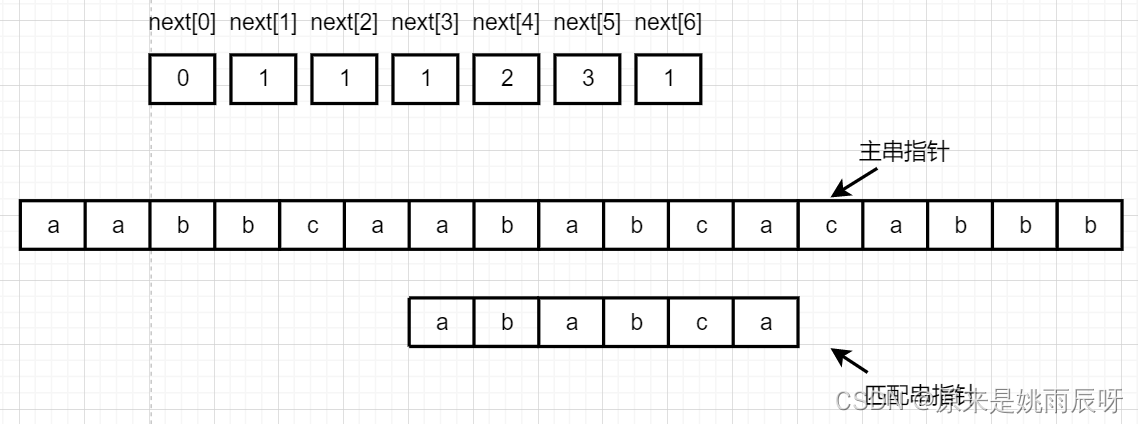

当匹配串指针超过匹配串长度时，KMP算法结束，匹配串在主串中的位置为主串指针位置-匹配串长度。
以上就是KMP算法的全部流程。

十万个为什么？？？：
1，为什么next数组可以表示匹配串当前元素匹配失败时下一次匹配指针的位置？
在回答这个问题之前首先应该清楚部分匹配值表的含义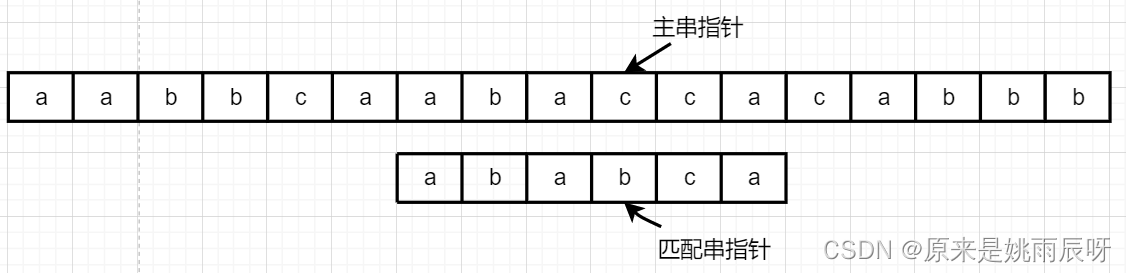

当前位置c和b不相等，但由于匹配串在b之前的子串{“aba”}，由于a=a，所以可以将主串指针前的元素c对应匹配串的a换成匹配串的第一个指针。
故指针的右移位数=已匹配的字符数-对应的部分匹配值
指针变化后的位置=(指针当前的位置)-指针的移动位数
已匹配的字符数=指针当前位置-1
又因为部分匹配值表均右移一位，转换为next数组。故指针变化后的位置=next+1。

1.5 近10年408数据结构考研真题(串，KMP模式匹配部分)

1，2015-08：

2，2019-09：