本文中我们将解释如何构建KG、分析它以及创建嵌入模型。

构建知识图谱
加载我们的数据。在本文中我们将从头创建一个简单的KG。
import pandas as pd
# Define the heads, relations, and tails
head = ['drugA', 'drugB', 'drugC', 'drugD', 'drugA', 'drugC', 'drugD', 'drugE', 'gene1', 'gene2','gene3', 'gene4', 'gene50', 'gene2', 'gene3', 'gene4']
relation = ['treats', 'treats', 'treats', 'treats', 'inhibits', 'inhibits', 'inhibits', 'inhibits', 'associated', 'associated', 'associated', 'associated', 'associated', 'interacts', 'interacts', 'interacts']
tail = ['fever', 'hepatitis', 'bleeding', 'pain', 'gene1', 'gene2', 'gene4', 'gene20', 'obesity', 'heart_attack', 'hepatitis', 'bleeding', 'cancer', 'gene1', 'gene20', 'gene50']
# Create a dataframe
df = pd.DataFrame({'head': head, 'relation': relation, 'tail': tail})
df
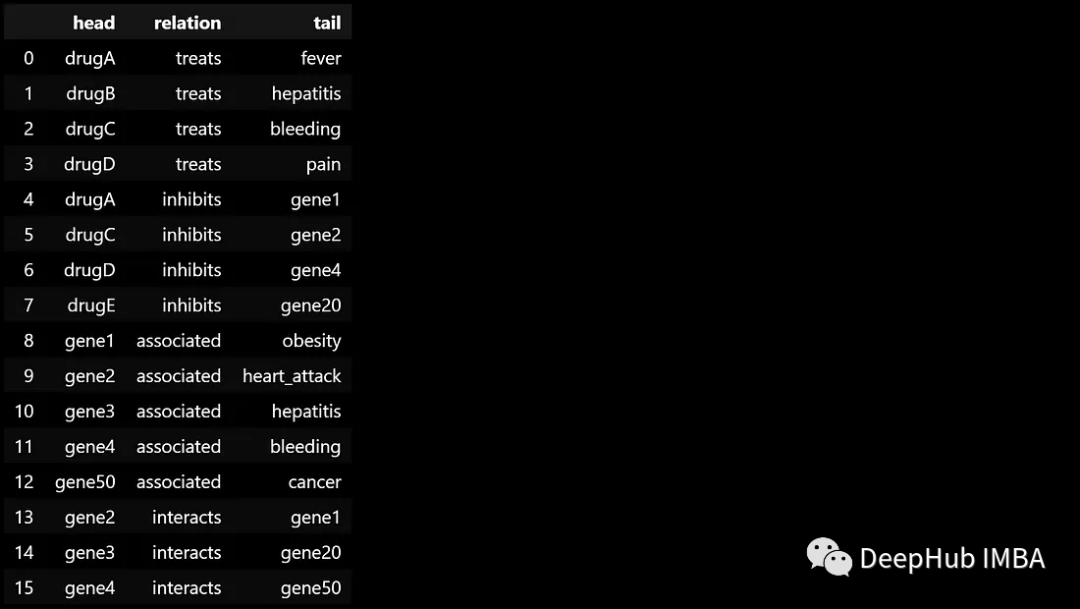
接下来,创建一个NetworkX图(G)来表示KG。DataFrame (df)中的每一行都对应于KG中的三元组(头、关系、尾)。add_edge函数在头部和尾部实体之间添加边,关系作为标签。
import networkx as nx
import matplotlib.pyplot as plt
# Create a knowledge graph
G = nx.Graph()
for _, row in df.iterrows():
G.add_edge(row['head'], row['tail'], label=row['relation'])
然后,绘制节点(实体)和边(关系)以及它们的标签。
# Visualize the knowledge graph
pos = nx.spring_layout(G, seed=42, k=0.9)
labels = nx.get_edge_attributes(G, 'label')
plt.figure(figsize=(12, 10))
nx.draw(G, pos, with_labels=True, font_size=10, node_size=700, node_color='lightblue', edge_color='gray', alpha=0.6)
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels, font_size=8, label_pos=0.3, verticalalignment='baseline')
plt.title('Knowledge Graph')
plt.show()
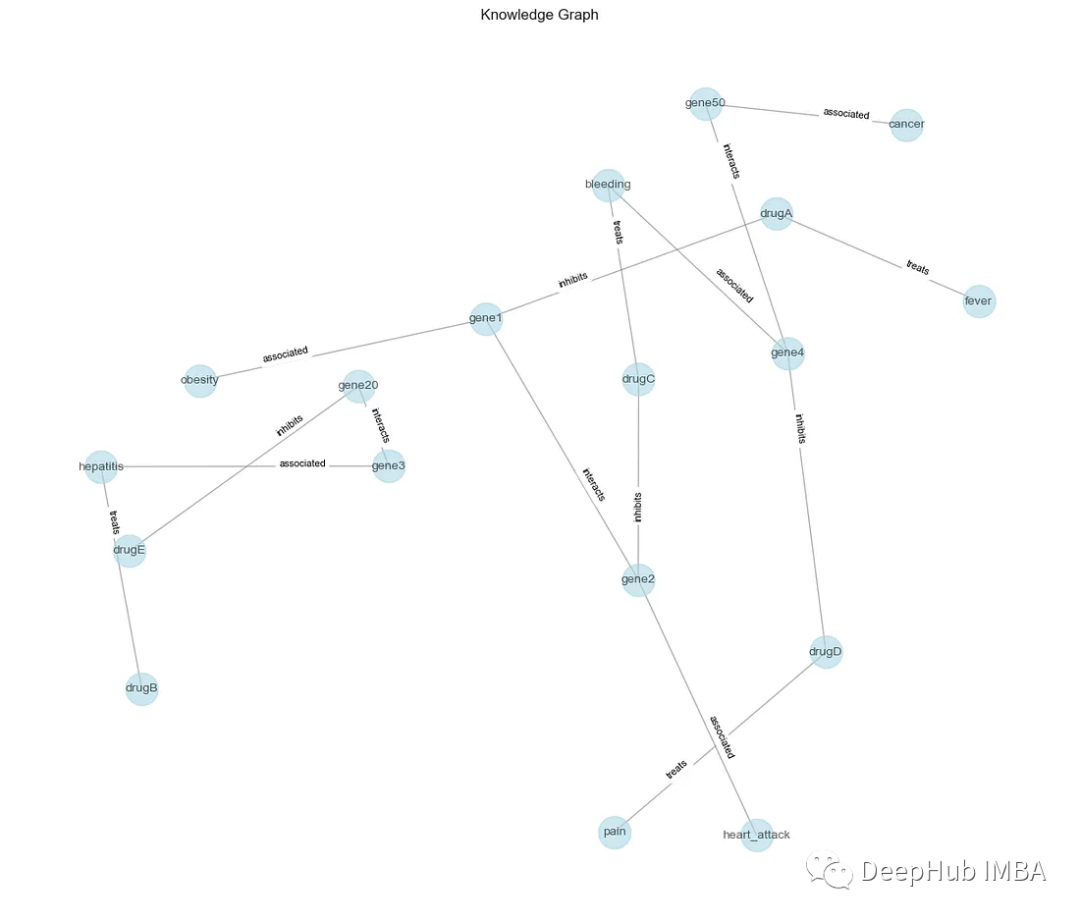
现在我们可以进行一些分析。
分析
对于KG,我们可以做的第一件事是查看它有多少个节点和边,并分析它们之间的关系。
num_nodes = G.number_of_nodes()
num_edges = G.number_of_edges()
print(f'Number of nodes: {num_nodes}')
print(f'Number of edges: {num_edges}')
print(f'Ratio edges to nodes: {round(num_edges / num_nodes, 2)}')

1、节点中心性分析
节点中心性度量图中节点的重要性或影响。它有助于识别图结构的中心节点。一些最常见的中心性度量是:
Degree centrality 计算节点上关联的边的数量。中心性越高的节点连接越紧密。
degree_centrality = nx.degree_centrality(G)
for node, centrality in degree_centrality.items():
print(f'{node}: Degree Centrality = {centrality:.2f}')
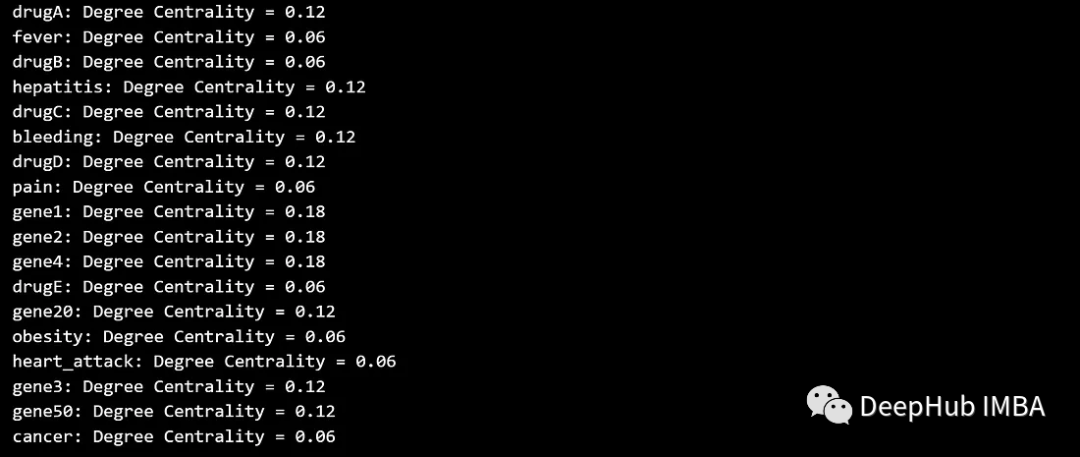
Betweenness centrality 衡量一个节点位于其他节点之间最短路径上的频率,或者说衡量一个节点对其他节点之间信息流的影响。具有高中间性的节点可以作为图的不同部分之间的桥梁。
betweenness_centrality = nx.betweenness_centrality(G)
for node, centrality in betweenness_centrality.items():
print(f'Betweenness Centrality of {node}: {centrality:.2f}')
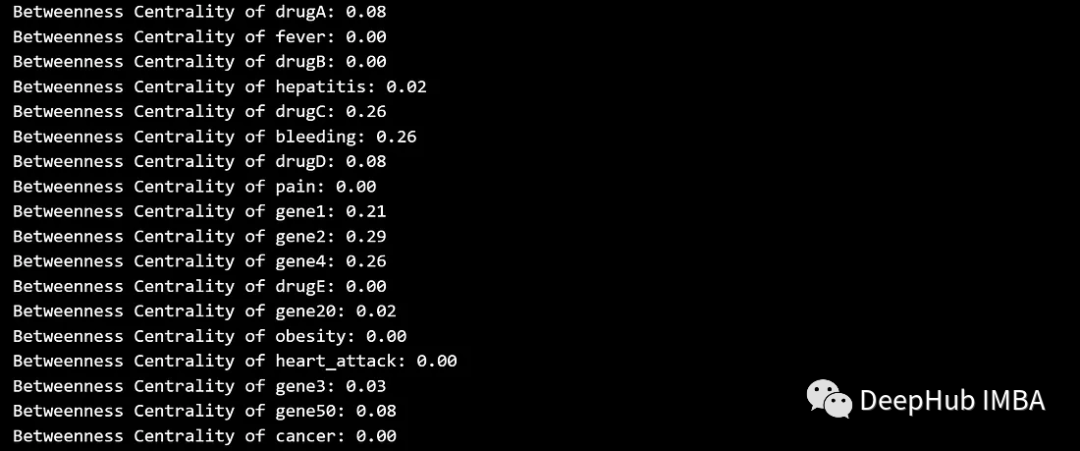
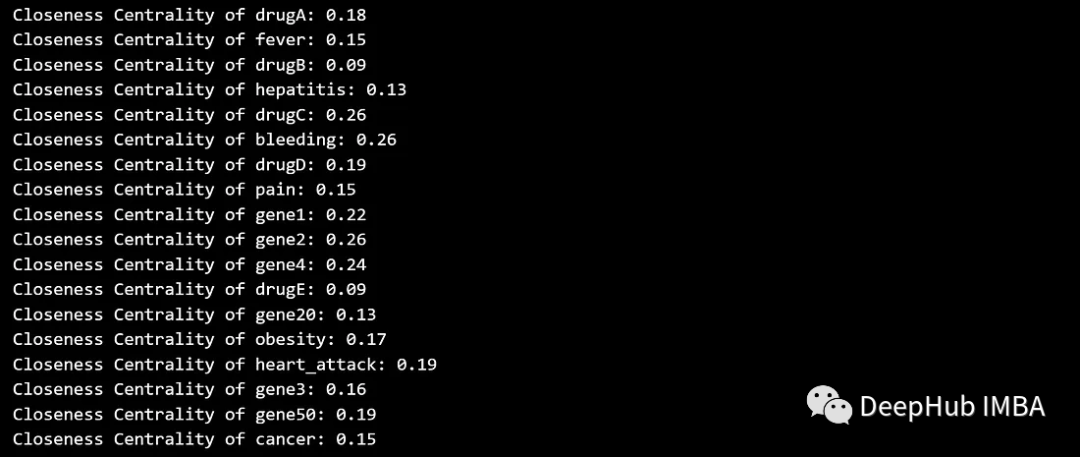
Closeness centrality 量化一个节点到达图中所有其他节点的速度。具有较高接近中心性的节点被认为更具中心性,因为它们可以更有效地与其他节点进行通信。
closeness_centrality = nx.closeness_centrality(G)
for node, centrality in closeness_centrality.items():
print(f'Closeness Centrality of {node}: {centrality:.2f}')
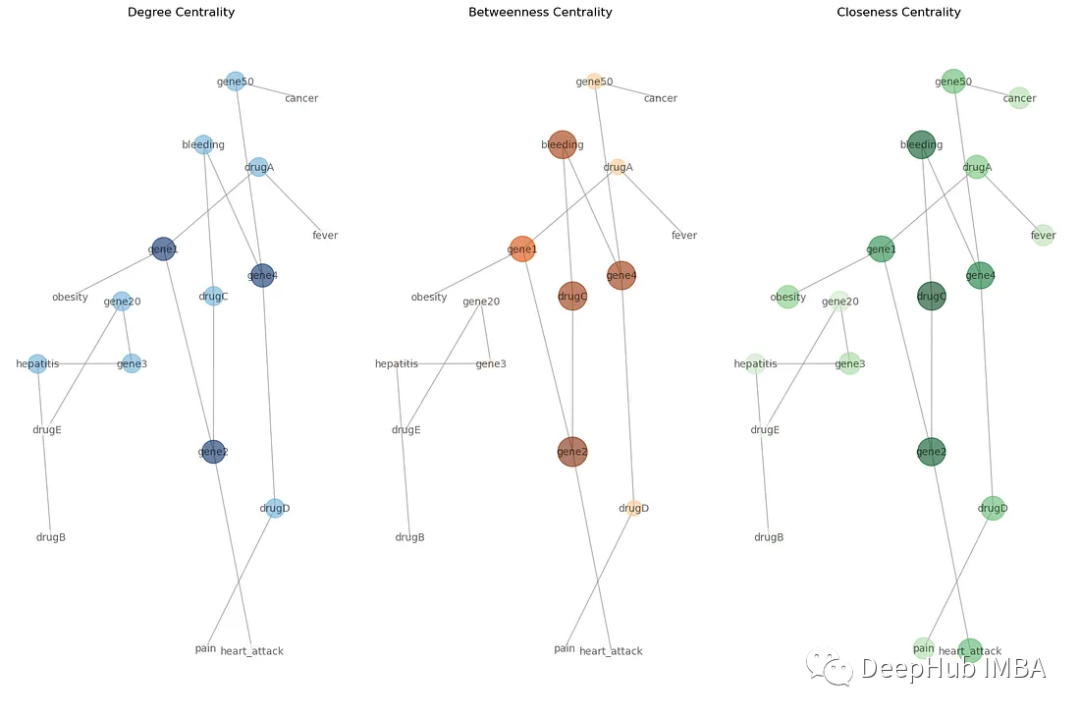
可视化
# Calculate centrality measures
degree_centrality = nx.degree_centrality(G)
betweenness_centrality = nx.betweenness_centrality(G)
closeness_centrality = nx.closeness_centrality(G)
# Visualize centrality measures
plt.figure(figsize=(15, 10))
# Degree centrality
plt.subplot(131)
nx.draw(G, pos, with_labels=True, font_size=10, node_size=[v * 3000 for v in degree_centrality.values()], node_color=list(degree_centrality.values()), cmap=plt.cm.Blues, edge_color='gray', alpha=0.6)
plt.title('Degree Centrality')
# Betweenness centrality
plt.subplot(132)
nx.draw(G, pos, with_labels=True, font_size=10, node_size=[v * 3000 for v in betweenness_centrality.values()], node_color=list(betweenness_centrality.values()), cmap=plt.cm.Oranges, edge_color='gray', alpha=0.6)
plt.title('Betweenness Centrality')
# Closeness centrality
plt.subplot(133)
nx.draw(G, pos, with_labels=True, font_size=10, node_size=[v * 3000 for v in closeness_centrality.values()], node_color=list(closeness_centrality.values()), cmap=plt.cm.Greens, edge_color='gray', alpha=0.6)
plt.title('Closeness Centrality')
plt.tight_layout()
plt.show()
2、最短路径分析
最短路径分析的重点是寻找图中两个节点之间的最短路径。这可以帮助理解不同实体之间的连通性,以及连接它们所需的最小关系数量。例如,假设你想找到节点“gene2”和“cancer”之间的最短路径:
source_node = 'gene2'
target_node = 'cancer'
# Find the shortest path
shortest_path = nx.shortest_path(G, source=source_node, target=target_node)
# Visualize the shortest path
plt.figure(figsize=(10, 8))
path_edges = [(shortest_path[i], shortest_path[i + 1]) for i in range(len(shortest_path) — 1)]
nx.draw(G, pos, with_labels=True, font_size=10, node_size=700, node_color='lightblue', edge_color='gray', alpha=0.6)
nx.draw_networkx_edges(G, pos, edgelist=path_edges, edge_color='red', width=2)
plt.title(f'Shortest Path from {source_node} to {target_node}')
plt.show()
print('Shortest Path:', shortest_path)
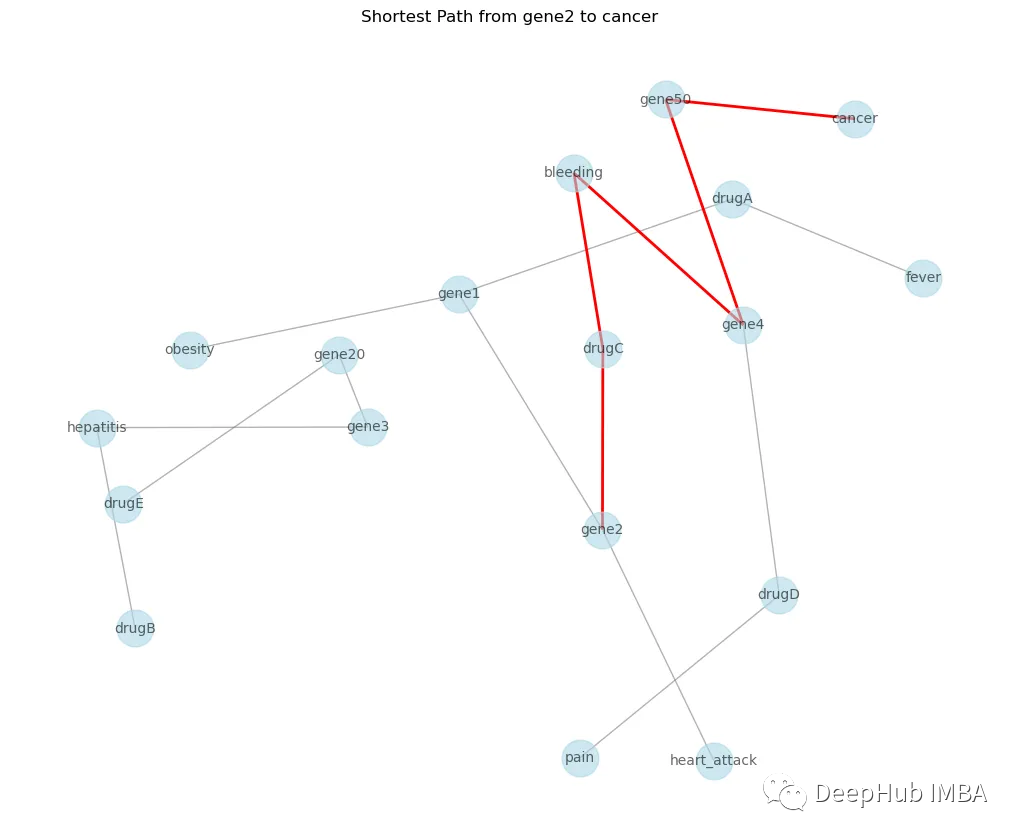
源节点“gene2”和目标节点“cancer”之间的最短路径用红色突出显示,整个图的节点和边缘也被显示出来。这可以帮助理解两个实体之间最直接的路径以及该路径上的关系。
图嵌入
图嵌入是连续向量空间中图中节点或边的数学表示。这些嵌入捕获图的结构和关系信息,允许我们执行各种分析,例如节点相似性计算和在低维空间中的可视化。
我们将使用node2vec算法,该算法通过在图上执行随机游走并优化以保留节点的局部邻域结构来学习嵌入。
from node2vec import Node2Vec
# Generate node embeddings using node2vec
node2vec = Node2Vec(G, dimensions=64, walk_length=30, num_walks=200, workers=4) # You can adjust these parameters
model = node2vec.fit(window=10, min_count=1, batch_words=4) # Training the model
# Visualize node embeddings using t-SNE
from sklearn.manifold import TSNE
import numpy as np
# Get embeddings for all nodes
embeddings = np.array([model.wv[node] for node in G.nodes()])
# Reduce dimensionality using t-SNE
tsne = TSNE(n_components=2, perplexity=10, n_iter=400)
embeddings_2d = tsne.fit_transform(embeddings)
# Visualize embeddings in 2D space with node labels
plt.figure(figsize=(12, 10))
plt.scatter(embeddings_2d[:, 0], embeddings_2d[:, 1], c='blue', alpha=0.7)
# Add node labels
for i, node in enumerate(G.nodes()):
plt.text(embeddings_2d[i, 0], embeddings_2d[i, 1], node, fontsize=8)
plt.title('Node Embeddings Visualization')
plt.show()
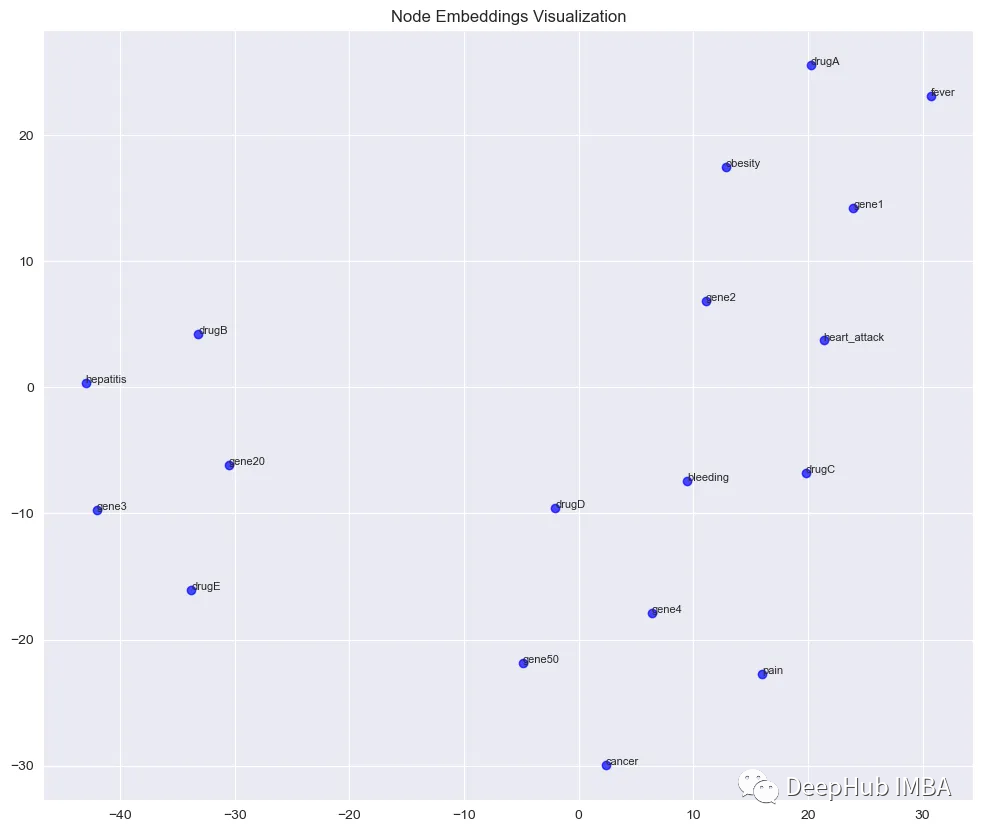
node2vec算法用于学习KG中节点的64维嵌入。然后使用t-SNE将嵌入减少到2维。并将结果以散点图方式进行可视化。不相连的子图是可以在矢量化空间中单独表示的
聚类
聚类是一种寻找具有相似特征的观察组的技术。因为是无监督算法,所以不必特别告诉算法如何对这些观察进行分组,算法会根据数据自行判断一组中的观测值(或数据点)比另一组中的其他观测值更相似。
1、K-means
K-means使用迭代细化方法根据用户定义的聚类数量(由变量K表示)和数据集生成最终聚类。
我们可以对嵌入空间进行K-means聚类。这样可以清楚地了解算法是如何基于嵌入对节点进行聚类的:
# Perform K-Means clustering on node embeddings
num_clusters = 3 # Adjust the number of clusters
kmeans = KMeans(n_clusters=num_clusters, random_state=42)
cluster_labels = kmeans.fit_predict(embeddings)
# Visualize K-Means clustering in the embedding space with node labels
plt.figure(figsize=(12, 10))
plt.scatter(embeddings_2d[:, 0], embeddings_2d[:, 1], c=cluster_labels, cmap=plt.cm.Set1, alpha=0.7)
# Add node labels
for i, node in enumerate(G.nodes()):
plt.text(embeddings_2d[i, 0], embeddings_2d[i, 1], node, fontsize=8)
plt.title('K-Means Clustering in Embedding Space with Node Labels')
plt.colorbar(label=”Cluster Label”)
plt.show()
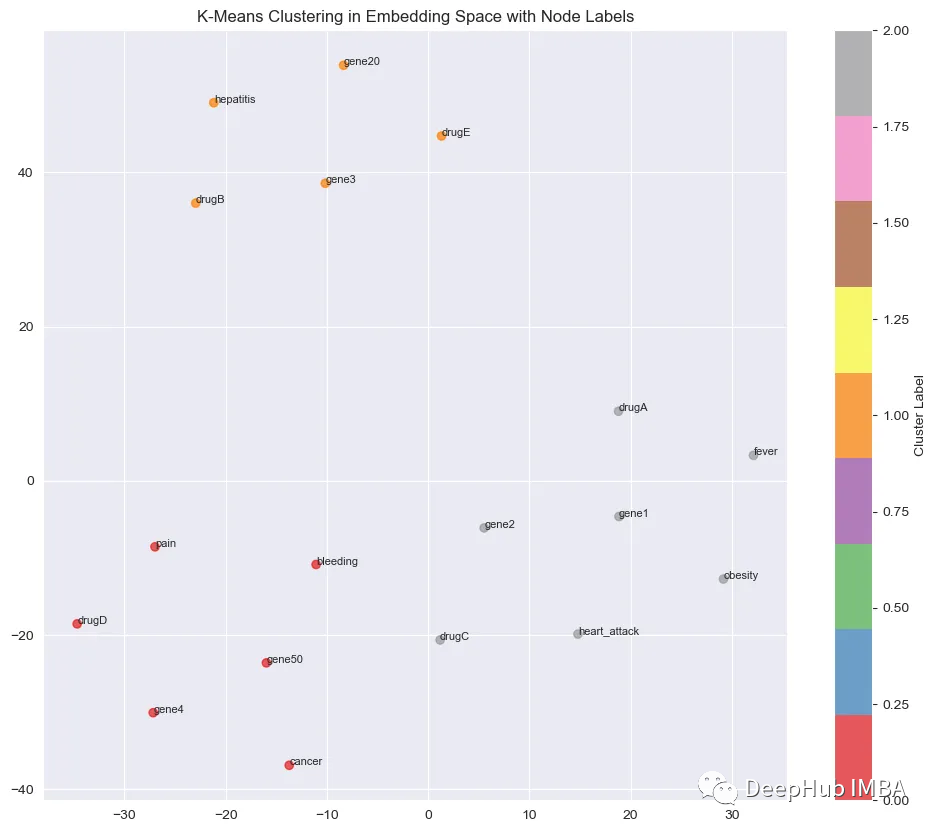
每种颜色代表一个不同的簇。现在我们回到原始图,在原始空间中解释这些信息:
from sklearn.cluster import KMeans
# Perform K-Means clustering on node embeddings
num_clusters = 3 # Adjust the number of clusters
kmeans = KMeans(n_clusters=num_clusters, random_state=42)
cluster_labels = kmeans.fit_predict(embeddings)
# Visualize clusters
plt.figure(figsize=(12, 10))
nx.draw(G, pos, with_labels=True, font_size=10, node_size=700, node_color=cluster_labels, cmap=plt.cm.Set1, edge_color=’gray’, alpha=0.6)
plt.title('Graph Clustering using K-Means')
plt.show()
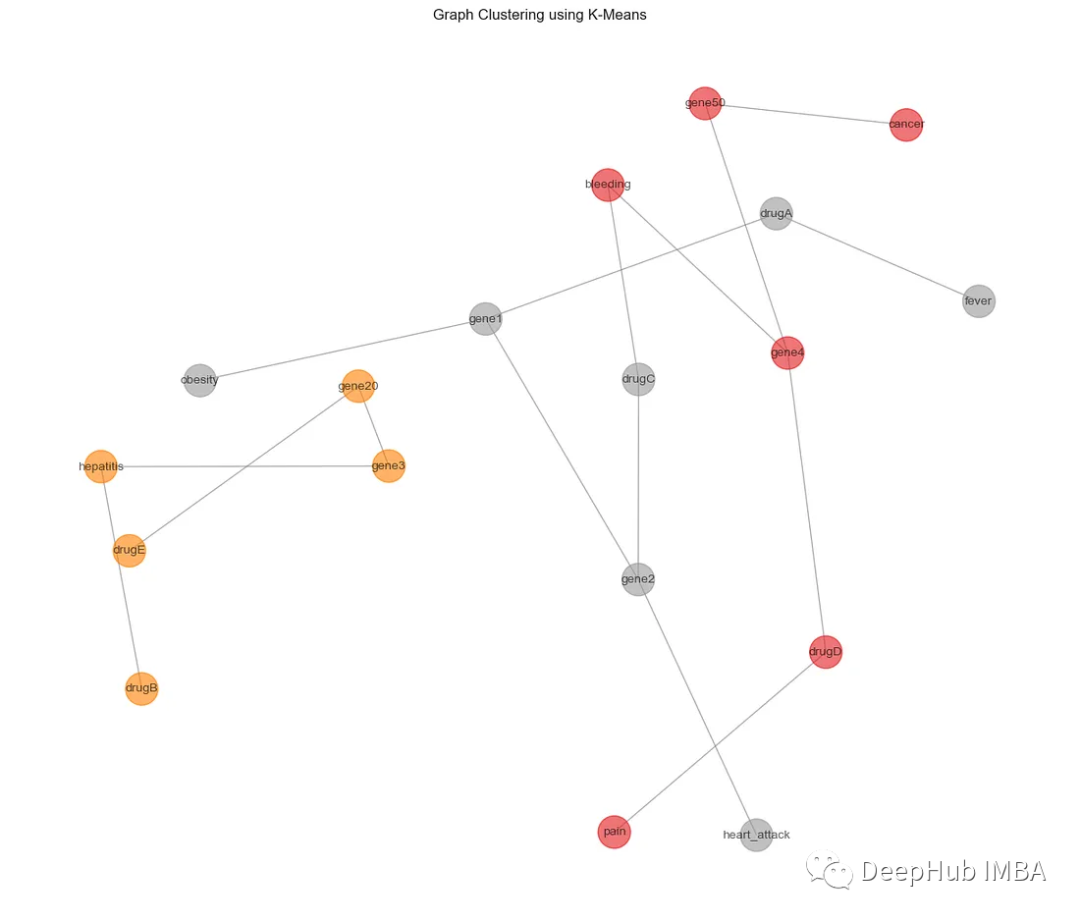
2、DBSCAN
DBSCAN是基于密度的聚类算法,并且不需要预设数量的聚类。它还可以将异常值识别为噪声。下面是如何使用DBSCAN算法进行图聚类的示例,重点是基于从node2vec算法获得的嵌入对节点进行聚类。
from sklearn.cluster import DBSCAN
# Perform DBSCAN clustering on node embeddings
dbscan = DBSCAN(eps=1.0, min_samples=2) # Adjust eps and min_samples
cluster_labels = dbscan.fit_predict(embeddings)
# Visualize clusters
plt.figure(figsize=(12, 10))
nx.draw(G, pos, with_labels=True, font_size=10, node_size=700, node_color=cluster_labels, cmap=plt.cm.Set1, edge_color='gray', alpha=0.6)
plt.title('Graph Clustering using DBSCAN')
plt.show()
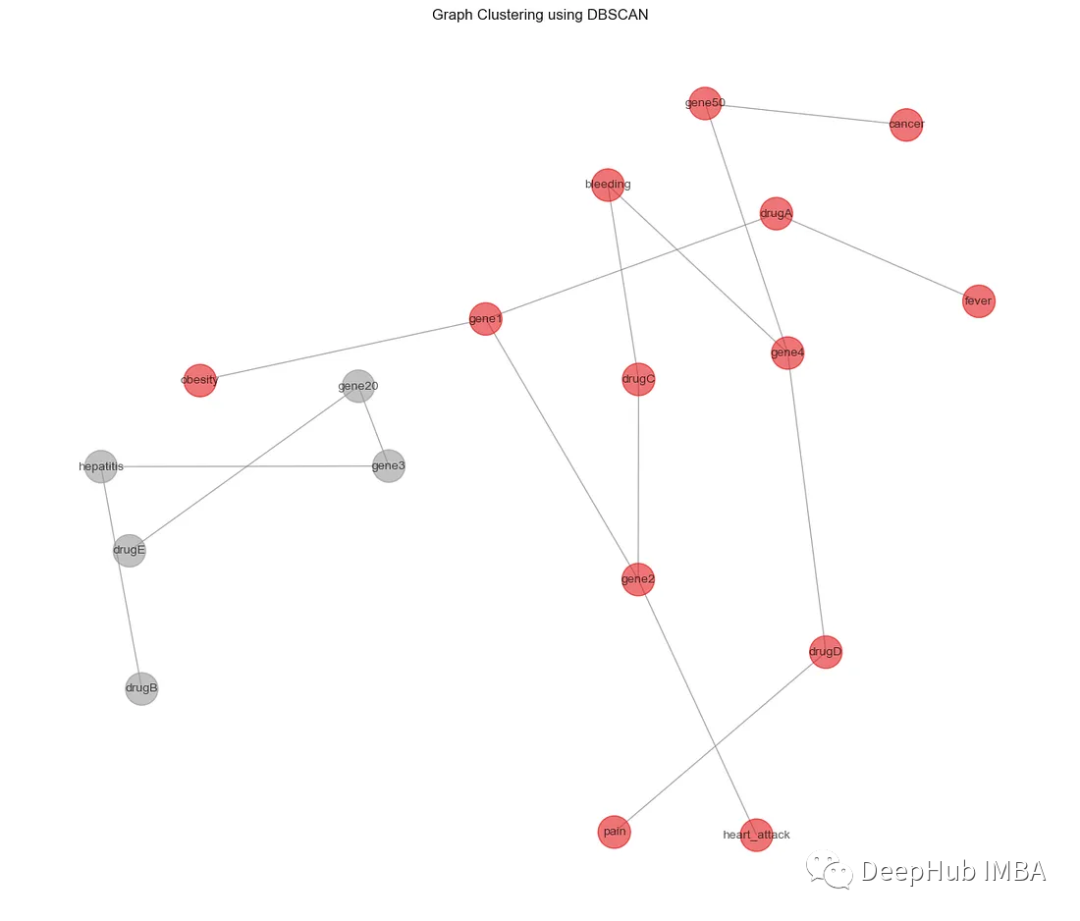
上面的eps参数定义了两个样本之间的最大距离,,min_samples参数确定了一个被认为是核心点的邻域内的最小样本数。可以看到DBSCAN将节点分配到簇,并识别不属于任何簇的噪声点。
总结
分析KGs可以为实体之间的复杂关系和交互提供宝贵的见解。通过结合数据预处理、分析技术、嵌入和聚类分析,可以发现隐藏的模式,并更深入地了解底层数据结构。
本文中的方法可以有效地可视化和探索KGs,是知识图谱学习中的必要的入门知识。
作者:Diego Lopez Yse