参考文献:
- Cheon J H, Kim A, Kim M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]//International conference on the theory and application of cryptology and information security. Springer, Cham, 2017: 409-437.
- 全同态加密:BGV
- 全同态加密:BFV
- CKKS explained series
文章目录
CKKS
不论是 LSB 编码的 BGV,还是 MSB 编码的 BFV,它们的同态运算都是对
Z
t
\mathbb Z_t
Zt 上明文的**精确计算**,因为**密文中的明文空间和噪声空间是分离的**。例如,在 BGV 中是
t
e
+
m
te+m
te+m,在 BFV 中是
δ
m
+
e
\delta m+e
δm+e。但是,这种精确计算是在同余意义下的,如果将明文视为实数,那么实际上同态运算时的噪声破坏了明文的 MSB
⌊
m
/
t
⌋
\lfloor m/t \rfloor
⌊m/t⌋,仅保留了 LSB
[
m
]
t
[m]_t
[m]t,如图:

而 CKKS 关注近似计算,它使得在密文中的明文空间和噪声空间是不分离的,噪声位于明文空间的 LSB 位置。也就是说,在 CKKS 中是
m
+
e
m+e
m+e,同态运算破坏明文的 LSB,但不破坏其 MSB。这也是合理的,可以将噪声破坏 LSB 视为**浮点运算的精度误差**。类似 BGV 做模切换,来使得噪声规模不会指数级增长;CKKS 也要做**重缩放**(*rescaling*),使得消息规模不会随电路深度而指数级增长,同时移除了 LSB 上的部分浮点误差。如图:

Canonical Embedding
符号:
Φ M ( x ) ∈ Z [ x ] \Phi_M(x) \in \mathbb Z[x] ΦM(x)∈Z[x], M M M 次单位根的分圆多项式,度数为 N = ϕ ( M ) N = \phi(M) N=ϕ(M)R : = Z [ x ] / ( Φ M ( x ) ) R := \mathbb Z[x]/(\Phi_M(x)) R:=Z[x]/(ΦM(x)),数域 Q [ x ] / ( ϕ M ( x ) ) \mathbb Q[x]/(\phi_M(x)) Q[x]/(ϕM(x)) 的子环(离散子群)R q = R / q R R_q = R/qR Rq=R/qR,商环 Z q [ x ] / ( Φ M ( x ) ) \mathbb Z_q[x]/(\Phi_M(x)) Zq[x]/(ΦM(x))S : = R [ x ] / ( Φ M ( x ) ) S := \mathbb R[x]/(\Phi_M(x)) S:=R[x]/(ΦM(x)),**分圆环**(cyclotomic ring),其中元素 a ( x ) a(x) a(x) 的系数构成向量 a ⃗ = ( a 0 , ⋯ , a N − 1 ) ∈ R N \vec a = (a_0,\cdots,a_{N-1}) \in \mathbb R^N a=(a0,⋯,aN−1)∈RN∥ a ∥ : = ∥ a ⃗ ∥ ∞ \|a\| := \|\vec a\|_{\infty} ∥a∥:=∥a∥∞,环元素的无穷范数∥ a ∥ 1 : = ∥ a ⃗ ∥ 1 \|a\|_1 := \|\vec a\|_1 ∥a∥1:=∥a∥1,环元素的L1 范数Z M ∗ : = { x ∈ Z M : g c d ( x , M ) = 1 } \mathbb Z_M^* := \{x \in \mathbb Z_M:gcd(x,M)=1\} ZM∗:={x∈ZM:gcd(x,M)=1},乘法群ξ M : = e x p ( − 2 π i / M ) \xi_M := exp(-2\pi i/M) ξM:=exp(−2πi/M), M M M 次本原单位根- 规范嵌入(canonical embedding) σ : S → C N \sigma: S \to \mathbb C^N σ:S→CN 定义为 σ ( a ) : = ( a ( ξ M j ) ) j ∈ Z M ∗ \sigma(a) := (a(\xi_M^j))_{j \in \mathbb Z_M^*} σ(a):=(a(ξMj))j∈ZM∗ 其中 a ∈ Q [ x ] / ( ϕ M ( x ) ) ⊂ S a \in \mathbb Q[x]/(\phi_M(x)) \sub S a∈Q[x]/(ϕM(x))⊂S
∥ a ∥ ∞ c a n : = ∥ σ ( a ) ∥ ∞ \|a\|_\infty^{can} := \|\sigma(a)\|_\infty ∥a∥∞can:=∥σ(a)∥∞,**规范嵌入范数**(*canonical embedding norm*)C R T M CRT_M CRTM, M M M 次本原单位根 ξ M j , j ∈ Z M ∗ \xi_M^j,\, j \in \mathbb Z_M^* ξMj,j∈ZM∗ 上的 Vandermonde 矩阵(可逆),使得 C R T M ⋅ a ⃗ = ( a ( ξ M j ) ) j ∈ Z M ∗ = σ ( a ) CRT_M \cdot \vec a = (a(\xi_M^j))_{j \in \mathbb Z_M^*} = \sigma(a) CRTM⋅a=(a(ξMj))j∈ZM∗=σ(a)(规范嵌入是线性变换)∥ U = ( u i j ) ∥ ∞ : = max i ∑ j ∣ u i j ∣ \|U=(u_{ij})\|_\infty := \max_{i} \sum_j |u_{ij}| ∥U=(uij)∥∞:=maxi∑j∣uij∣,**矩阵的无穷范数**c M : = ∥ C R T M − 1 ∥ ∞ c_M := \|CRT_M^{-1}\|_\infty cM:=∥CRTM−1∥∞,环常数(ring constant),仅与 M M M 有关
性质:
∀ a , b ∈ S \forall a,b \in S ∀a,b∈S,有 ∥ a ⋅ b ∥ ∞ c a n ≤ ∥ a ∥ ∞ c a n ⋅ ∥ b ∥ ∞ c a n \|a \cdot b\|_\infty^{can} \le \|a\|_\infty^{can} \cdot \|b\|_\infty^{can} ∥a⋅b∥∞can≤∥a∥∞can⋅∥b∥∞can∀ a ∈ S \forall a \in S ∀a∈S,有 ∥ a ∥ ∞ c a n ≤ ∥ a ∥ 1 \|a\|_\infty^{can} \le \|a\|_1 ∥a∥∞can≤∥a∥1∀ a ∈ S \forall a \in S ∀a∈S,有 ∥ a ∥ ∞ ≤ c M ⋅ ∥ a ∥ ∞ c a n \|a\|_\infty \le c_M \cdot \|a\|_\infty^{can} ∥a∥∞≤cM⋅∥a∥∞can
Gaussian Distributions
定义线性子空间:
H
:
=
{
z
⃗
=
(
z
j
)
j
∈
Z
M
∗
∈
C
N
:
z
j
=
z
ˉ
−
j
,
∀
j
∈
Z
M
∗
}
\mathbb H := \{ \vec z = (z_j)_{j \in \mathbb Z_M^*} \in \mathbb C^N:\, z_j = \bar z_{-j},\, \forall j \in \mathbb Z_M^* \}
H:={z=(zj)j∈ZM∗∈CN:zj=zˉ−j,∀j∈ZM∗}
也就是所有满足共轭约束的向量。可以验证,作为内积空间(inner product space)
H
≅
R
N
\mathbb H \cong \mathbb R^N
H≅RN,关于**幺正矩阵**(unitary basis matrix,酉矩阵)
U
=
[
1
2
I
i
2
J
1
2
J
−
i
2
I
]
∈
C
N
×
N
U = \begin{bmatrix} \frac{1}{\sqrt 2}I & \frac{i}{\sqrt 2}J\\ \frac{1}{\sqrt 2}J & \frac{-i}{\sqrt 2}I\\ \end{bmatrix} \in \mathbb C^{N \times N}
U=[21I21J2iJ2−iI]∈CN×N
其中
I
∈
C
N
/
2
×
N
/
2
I \in C^{N/2 \times N/2}
I∈CN/2×N/2 是单位阵,
J
J
J 是其**翻转矩阵**(reversal matrix)
J
=
[
0
⋯
0
1
0
⋯
1
0
⋮
1
⋯
0
0
]
∈
C
N
/
2
×
N
/
2
J = \begin{bmatrix} 0 & \cdots & 0 & 1\\ 0 & \cdots & 1 & 0\\ & \vdots\\ 1 & \cdots & 0 & 0\\ \end{bmatrix} \in \mathbb C^{N/2 \times N/2}
J=⎣⎡001⋯⋯⋮⋯010100⎦⎤∈CN/2×N/2
易知,共轭转置
U
H
=
U
−
1
U^H = U^{-1}
UH=U−1,并且有:
H
=
U
⋅
R
N
\mathbb H = U \cdot \mathbb R^N
H=U⋅RN,
U
H
⋅
H
=
R
N
U^H \cdot \mathbb H = \mathbb R^N
UH⋅H=RN
对于
r
>
0
r > 0
r>0,定义 *Gaussian function* 为
ρ
r
:
R
n
→
(
0
,
1
]
\rho_r: \mathbb R^n \to (0,1]
ρr:Rn→(0,1] 为
ρ
r
(
z
⃗
)
=
exp
(
−
π
∥
z
⃗
∥
2
2
r
2
)
\rho_r(\vec z) = \exp\left(\frac{-\pi \|\vec z\|_2^2}{r^2}\right)
ρr(z)=exp(r2−π∥z∥22)
对于
r
⃗
=
(
r
1
,
⋯
,
r
N
)
∈
(
R
+
)
N
\vec r = (r_1,\cdots,r_N) \in (\mathbb R^+)^N
r=(r1,⋯,rN)∈(R+)N,
H
\mathbb H
H 上的 *elliptical Gaussian distribution*
Γ
r
⃗
\Gamma_{\vec r}
Γr 定义为:根据
Γ
r
i
\Gamma_{r_i}
Γri 独立采样
z
i
∈
R
z_i \in \mathbb R
zi∈R,然后输出
U
⋅
z
⃗
U \cdot \vec z
U⋅z
上述连续高斯分布同时诱导了环
S
:
=
R
[
x
]
/
(
ϕ
M
(
x
)
)
S := \mathbb R[x]/(\phi_M(x))
S:=R[x]/(ϕM(x)) 上的分布
Ψ
r
⃗
\Psi_{\vec r}
Ψr,它的采样输出为:
e
⃗
:
=
C
R
T
M
−
1
⋅
U
⋅
z
⃗
\vec e := CRT_M^{-1} \cdot U \cdot \vec z
e:=CRTM−1⋅U⋅z,就是
e
(
x
)
∈
S
e(x) \in S
e(x)∈S 在基
1
,
x
,
x
2
,
⋯
,
x
N
−
1
1,x,x^2,\cdots,x^{N-1}
1,x,x2,⋯,xN−1 上的组合系数。
为了获得离散高斯分布,执行圆整操作
χ
:
=
⌊
Ψ
r
⃗
⌉
R
∨
\chi := \lfloor \Psi_{\vec r}\rceil_{R^\vee}
χ:=⌊Ψr⌉R∨,即把采样结果
e
∈
S
e \in S
e∈S 最近的环元素
e
′
∈
R
∨
e' \in R^\vee
e′∈R∨ 作为离散采样结果。其中
R
∨
R^\vee
R∨ 是环
R
R
R 的 *dual fractional ideal*(这啥?),我数学不好没看懂 (╥╯^╰╥)
SIMD
CKKS 使用 RLWE,类似 BGV 使用分圆多项式
ϕ
M
(
x
)
\phi_M(x)
ϕM(x),根据 CRT 可以将密文分成
N
N
N 个的**槽**(slot),从而可以实现 SIMD。
基于 RLWE 的密码方案的明文空间可以被视作
S
S
S 的子集,其中的元素是
∥
m
∥
∞
c
a
n
≪
q
\|m\|_\infty^{can} \ll q
∥m∥∞can≪q 的那些
m
(
x
)
m(x)
m(x)
令
ξ
M
\xi_M
ξM 是一个复平面上的
M
M
M 次本原单位根。分圆环
S
:
=
R
[
x
]
/
(
Φ
M
(
x
)
)
S := \mathbb R[x]/(\Phi_M(x))
S:=R[x]/(ΦM(x)),对于
a
∈
S
a \in S
a∈S,规范嵌入为
σ
(
a
)
:
=
(
a
(
ξ
M
j
)
)
j
∈
Z
M
∗
∈
C
N
\sigma(a) := (a(\xi_M^j))_{j \in \mathbb Z_M^*} \in \mathbb C^N
σ(a):=(a(ξMj))j∈ZM∗∈CN。
确切地说,由于
a
∈
S
a \in S
a∈S 是实系数多项式,因此
a
(
ξ
−
j
)
=
a
(
ξ
j
‾
)
=
a
(
ξ
j
)
‾
a(\xi^{-j}) = a(\overline{\xi^j}) = \overline{a(\xi^j)}
a(ξ−j)=a(ξj)=a(ξj),规范嵌入的**像**
I
m
(
σ
)
=
H
⊂
C
N
Im(\sigma) = \mathbb H \sub \mathbb C^N
Im(σ)=H⊂CN,容易看出**同构**
H
≅
S
\mathbb H \cong S
H≅S
由于
H
\mathbb H
H 中的元素满足共轭约束,因此令
T
T
T 是
Z
M
∗
\mathbb Z_M^*
ZM∗ 的乘法子群,使得
Z
M
∗
/
T
=
{
±
1
}
\mathbb Z_M^*/T = \{\pm 1\}
ZM∗/T={±1},那么考虑**自然投影**(*natural projection*)
π
:
H
→
C
N
/
2
\pi: \mathbb H \to \mathbb C^{N/2}
π:H→CN/2
π
(
(
z
j
)
j
∈
Z
M
∗
)
:
=
(
z
j
)
j
∈
T
\pi((z_j)_{j \in \mathbb Z_M^*}) := (z_j)_{j \in T}
π((zj)j∈ZM∗):=(zj)j∈T
那么关于映射
π
\pi
π,有**同构**
H
≅
C
N
/
2
\mathbb H \cong \mathbb C^{N/2}
H≅CN/2
由于
R
=
Z
[
x
]
/
(
ϕ
(
x
)
)
R = \mathbb Z[x]/(\phi(x))
R=Z[x]/(ϕ(x)),因此它有一组
Z
−
\mathbb Z-
Z−基
{
1
,
x
,
⋯
,
x
N
−
1
}
\{1,x,\cdots,x^{N-1}\}
{1,x,⋯,xN−1},这利用规范嵌入
σ
(
⋅
)
\sigma(\cdot)
σ(⋅) 可以得到一个秩
N
N
N 的**理想格**(*ideal lattice*)
σ
(
R
)
\sigma(R)
σ(R),基为
{
σ
(
1
)
,
σ
(
x
)
,
⋯
,
σ
(
x
N
−
1
)
}
\{\sigma(1),\sigma(x),\cdots,\sigma(x^{N-1})\}
{σ(1),σ(x),⋯,σ(xN−1)}
现在,我们已经有了
S
→
H
S \to \mathbb H
S→H 的同构
σ
\sigma
σ,以及
H
→
C
N
/
2
\mathbb H \to \mathbb C^{N/2}
H→CN/2 的同构
π
\pi
π,那么就有同构映射
π
∘
σ
:
(
S
,
∥
⋅
∥
∞
c
a
n
)
→
(
C
N
/
2
,
∥
⋅
∥
∞
)
\pi \circ \sigma: (S,\, \|\cdot\|_\infty^{can}) \to \mathbb (C^{N/2},\, \|\cdot\|_\infty)
π∘σ:(S,∥⋅∥∞can)→(CN/2,∥⋅∥∞)
由于
R
⊂
S
R \sub S
R⊂S 是子环,因此
σ
(
R
)
⊂
H
\sigma(R) \sub \mathbb H
σ(R)⊂H 是离散子群,从而
π
(
σ
(
R
)
)
⊂
C
N
/
2
\pi(\sigma(R)) \sub \mathbb C^{N/2}
π(σ(R))⊂CN/2 是有限精度的浮点数向量集合。如图:

所以,任给一个复向量
z
⃗
∈
C
N
/
2
\vec z \in \mathbb C^{N/2}
z∈CN/2,它的原像
π
−
1
(
z
⃗
)
\pi^{-1}(\vec z)
π−1(z) 不一定落在格
σ
(
R
)
\sigma(R)
σ(R) 上,需要**就近圆整**
⌊
π
−
1
(
z
⃗
)
⌉
σ
(
R
)
\lfloor \pi^{-1}(\vec z) \rceil_{\sigma(R)}
⌊π−1(z)⌉σ(R),得到最接近的**格点**,这就导致了圆整误差。为了提高浮点数精度,可以设置一个 *scaling factor*
Δ
≥
1
\Delta \ge 1
Δ≥1,先
z
⃗
′
=
Δ
⋅
z
⃗
\vec z' = \Delta \cdot \vec z
z′=Δ⋅z,然后
π
−
1
(
σ
−
1
(
z
⃗
′
)
)
∈
R
\pi^{-1}(\sigma^{-1}(\vec z')) \in R
π−1(σ−1(z′))∈R 得到对应的明文。

CKKS 的编码、解码算法为:

LHE
CKKS 使用了:BGV 的密钥切换技术、模切换技术、打包技术,BFV 的重线性化技术。抽象的来说,CKKS 方案如下(注意 Enc 算法):

CKKS 使用模切换过程,来移除密文中明文信息的被噪声淹没的 LSB 部分,叫做重缩放(rescaling)。固定 base
p
>
0
p>0
p>0 和模数
q
0
>
0
q_0 > 0
q0>0(都不必是素数)。对于深度为
L
L
L 的电路,设置梯子为
q
l
=
q
l
⋅
q
0
q_l = q^l \cdot q_0
ql=ql⋅q0,第
l
l
l 层的密文属于
R
q
l
2
R_{q_l}^2
Rql2

同态运算时,密文中的消息和噪声的规模都会增长。为了方便管理密文,还要在
c
c
c 上附加上一些标签:层级
0
≤
l
≤
L
0 \le l \le L
0≤l≤L,消息上界
v
∈
R
v \in \mathbb R
v∈R,噪声上界
B
∈
R
B \in \mathbb R
B∈R

另外,同态运算之前,需要参与运算的两个密文
(
c
,
l
,
v
,
B
)
,
(
c
′
,
l
′
,
v
′
,
B
′
)
(c,l,v,B),\, (c',l',v',B')
(c,l,v,B),(c′,l′,v′,B′) 的 **level 保证一致**。假设
l
′
<
l
l' < l
l′<l,那么需要将
c
c
c 降级到
l
′
l'
l′ 级的
R
q
l
′
R_{q_{l'}}
Rql′ 上:
- 如果使用 RS 过程, c ↦ R S ( c ) c \mapsto RS(c) c↦RS(c),那么消息从 m m m 变化为 q l ′ q l m \frac{q_{l'}}{q_l}m qlql′m
- 而直接简单模约简, c ↦ c m o d q l ′ c \mapsto c \mod q_{l'} c↦cmodql′,这不会改变消息 m m m

如果选取
M
=
2
k
+
1
M = 2^{k+1}
M=2k+1,那么
ϕ
M
(
x
)
=
x
N
+
1
\phi_M(x) = x^N+1
ϕM(x)=xN+1,其中
N
=
2
k
N = 2^k
N=2k,环
R
=
Z
[
x
]
/
(
x
N
+
1
)
R = \mathbb Z[x]/(x^N+1)
R=Z[x]/(xN+1) 有良好的性质:
- 此时 R ∨ = N − 1 ⋅ R R^\vee = N^{-1} \cdot R R∨=N−1⋅R,从而噪声 e ′ ∈ R ∨ e' \in R^\vee e′∈R∨ 可以转化为 e = N ⋅ e ′ ∈ R e = N \cdot e' \in R e=N⋅e′∈R,它的各个系数是相互独立的离散高斯采样。
- 圆整运算可以高效计算,因为 C R T M CRT_M CRTM 是正交阵,因此 ⌊ a ( x ) ⌉ σ ( R ) = ∑ i ⌊ a i ⌉ Z ⋅ x i \lfloor a(x) \rceil_{\sigma(R)} = \sum_i \lfloor a_i\rceil_\mathbb Z \cdot x^i ⌊a(x)⌉σ(R)=∑i⌊ai⌉Z⋅xi(多项式圆整就是各项系数分别圆整)
CKKS 使用了多种分布(我不知道为何需要这么多。为了效率?为了安全性?):
D G ( σ 2 ) DG(\sigma^2) DG(σ2):实数 σ > 0 \sigma>0 σ>0,采样 Z N \mathbb Z^N ZN 上向量,各分量是方差为 σ 2 \sigma^2 σ2 的 Z \mathbb Z Z 上独立的离散高斯采样H W T ( h ) HWT(h) HWT(h):正整数 h h h,采样 { 0 , ± 1 } N \{0,\pm 1\}^N {0,±1}N 上向量(signed binary vectors),汉明重量为 h h hZ O ( ρ ) ZO(\rho) ZO(ρ):实数 0 ≤ ρ ≤ 1 0 \le \rho \le 1 0≤ρ≤1,采样 { 0 , ± 1 } N \{0,\pm 1\}^N {0,±1}N 上向量,它的各个分量以 ρ / 2 \rho/2 ρ/2 的概率为 1 , − 1 1,-1 1,−1,以 1 − ρ 1-\rho 1−ρ 的概率为 0 0 0
CKKS 方案如下:

我们说一个密文
(
c
∈
R
q
l
2
,
l
,
v
,
B
)
(c \in R_{q_l}^2,l,v,B)
(c∈Rql2,l,v,B) 是
m
∈
S
m \in S
m∈S 的**有效密文**(*valid encryption*),如果
∥
m
∥
∞
c
a
n
≤
v
\|m\|_\infty^{can} \le v
∥m∥∞can≤v 且
<
c
,
s
k
>
=
m
+
2
m
o
d
q
l
<c,sk> = m+2 \mod q_l
<c,sk>=m+2modql,其中
e
∈
S
e \in S
e∈S 满足
∥
e
∥
∞
c
a
n
≤
B
\|e\|_\infty^{can} \le B
∥e∥∞can≤B。可以证明:

为了达到
λ
−
\lambda-
λ−比特的安全性,需要使得
N
≥
λ
+
110
7.2
log
(
P
⋅
q
L
)
N \ge \frac{\lambda+110}{7.2} \log(P \cdot q_L)
N≥7.2λ+110log(P⋅qL)。由于
q
L
q_L
qL 是梯子中最大的模数,因此让
P
P
P 接近于
q
L
q_L
qL 即可。对于
λ
=
80
\lambda = 80
λ=80,文章中设置
σ
=
3.2
\sigma = 3.2
σ=3.2,
h
=
64
h = 64
h=64。
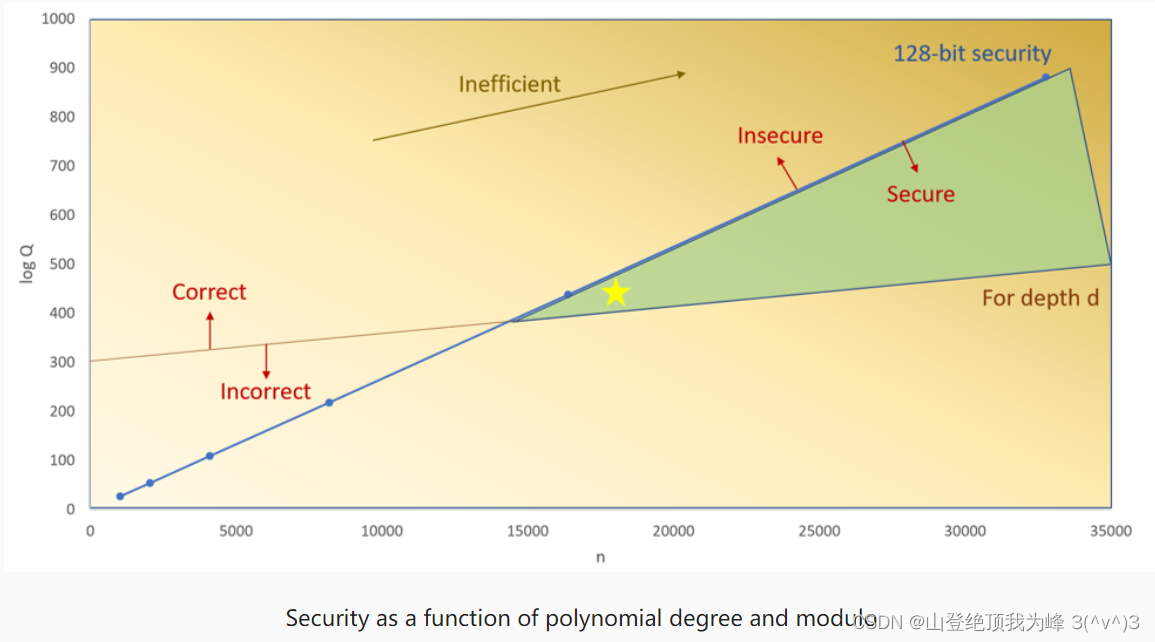
下图展示了安全性和计算效率之间的 tradeoff:为了提高安全性,这需要提升分圆多项式的次数
N
N
N,即使我们不需要太多的(
N
/
2
N/2
N/2个) 明文槽。
Rotate
根据数论知识,域扩张
Q
(
ξ
M
)
/
Q
\mathbb Q(\xi_M)/\mathbb Q
Q(ξM)/Q 的 **Galois 群**
G
a
l
:
=
G
a
l
(
Q
(
ξ
M
)
/
Q
)
Gal := Gal(\mathbb Q(\xi_M)/\mathbb Q)
Gal:=Gal(Q(ξM)/Q) 是个同构于
Z
M
∗
\mathbb Z_M^*
ZM∗ 的乘法群,其中的元素是**自同构映射**:
κ
k
:
m
(
x
)
↦
m
(
x
k
)
,
∀
g
c
d
(
k
,
M
)
=
1
\kappa_k: m(x) \mapsto m(x^k),\, \forall gcd(k,M)=1
κk:m(x)↦m(xk),∀gcd(k,M)=1
一个明文多项式为
m
(
x
)
∈
R
⊂
Q
(
ξ
M
)
m(x) \in R \sub \mathbb Q(\xi_M)
m(x)∈R⊂Q(ξM),解码后对应的明文向量是
z
⃗
=
π
(
σ
(
m
(
x
)
)
)
∈
C
N
/
2
\vec z = \pi(\sigma(m(x))) \in \mathbb C^{N/2}
z=π(σ(m(x)))∈CN/2。对于任意的
i
,
j
∈
T
⊂
Z
M
∗
i,j \in T \sub \mathbb Z_M^*
i,j∈T⊂ZM∗,令
k
=
j
−
1
⋅
i
m
o
d
M
k = j^{-1} \cdot i \mod M
k=j−1⋅imodM,那么计算
m
′
=
κ
k
(
m
)
m' = \kappa_k(m)
m′=κk(m),满足
z
j
′
=
m
′
(
ξ
M
j
)
=
κ
(
m
(
ξ
M
j
)
)
=
m
(
ξ
M
j
k
)
=
m
(
ξ
M
i
)
=
z
i
z_j' = m'(\xi_M^j) = \kappa(m(\xi_M^j)) = m(\xi_M^{jk}) = m(\xi_M^{i}) = z_i
zj′=m′(ξMj)=κ(m(ξMj))=m(ξMjk)=m(ξMi)=zi
也就是说,自同构映射
κ
k
\kappa_k
κk 可以实现把明文信息从槽
i
i
i 搬移到槽
j
j
j
定义向量
(
c
i
)
I
(c_i)_I
(ci)I 上的自同构映射为:
κ
k
(
(
c
i
)
I
)
:
=
(
κ
k
(
c
i
)
)
I
\kappa_k((c_i)_I) := (\kappa_k(c_i))_I
κk((ci)I):=(κk(ci))I,可以验证,如果
c
∈
R
q
l
2
c \in R_{q_l}^2
c∈Rql2 是明文
m
∈
R
m \in R
m∈R 在私钥
(
1
,
s
)
(1,s)
(1,s) 下的有效密文,那么
κ
k
(
c
)
∈
R
q
l
2
\kappa_k(c) \in R_{q_l}^2
κk(c)∈Rql2 是明文
κ
k
(
m
)
∈
R
\kappa_k(m) \in R
κk(m)∈R 在私钥
(
1
,
κ
k
(
s
)
)
(1,\kappa_k(s))
(1,κk(s)) 下的有效密文。
类似 BGV 的 Pack / Unpack 技术,将密文的密钥切换变换
τ
(
1
,
s
)
→
(
1
,
κ
k
(
s
)
)
\tau_{(1,s) \to (1,\kappa_k(s))}
τ(1,s)→(1,κk(s)) 和
τ
(
1
,
κ
k
(
s
)
)
→
(
1
,
s
)
\tau_{(1,\kappa_k(s)) \to (1,s)}
τ(1,κk(s))→(1,s) 作为公钥发布,从而实现密文上各个槽里的明文信息的任意搬移。
版权归原作者 山登绝顶我为峰 3(^v^)3 所有, 如有侵权,请联系我们删除。