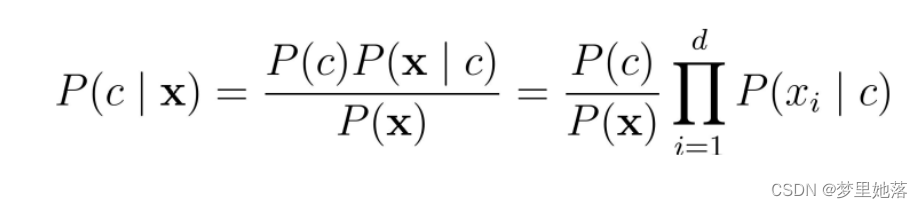0
0

机器学习--使用朴素贝叶斯进行垃圾邮件分类

一、学习背景

垃圾邮件的问题一直困扰着人们，传统的垃圾邮件分类的方法主要有"关键词法"和"校验码法"等，然而这两种方法效果并不理想。其中，如果使用的是“关键词”法，垃圾邮件中如果这个关键词被拆开则可能识别不了，比如，“中奖”如果被拆成“中 --- 奖”可能会识别不了。后来，直到提出了使用“贝叶斯”的方法才使得垃圾邮件的分类达到一个较好的效果，而且随着邮件数目越来越多，贝叶斯分类的效果会更加好。

我们想采用的分类方法是通过多个词来判断是否为垃圾邮件，但这个概率难以估计，通过贝叶斯公式，可以转化为求垃圾邮件中这些词出现的概率。

二、贝叶斯公式

贝叶斯定理 由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件 概率 之间的关系

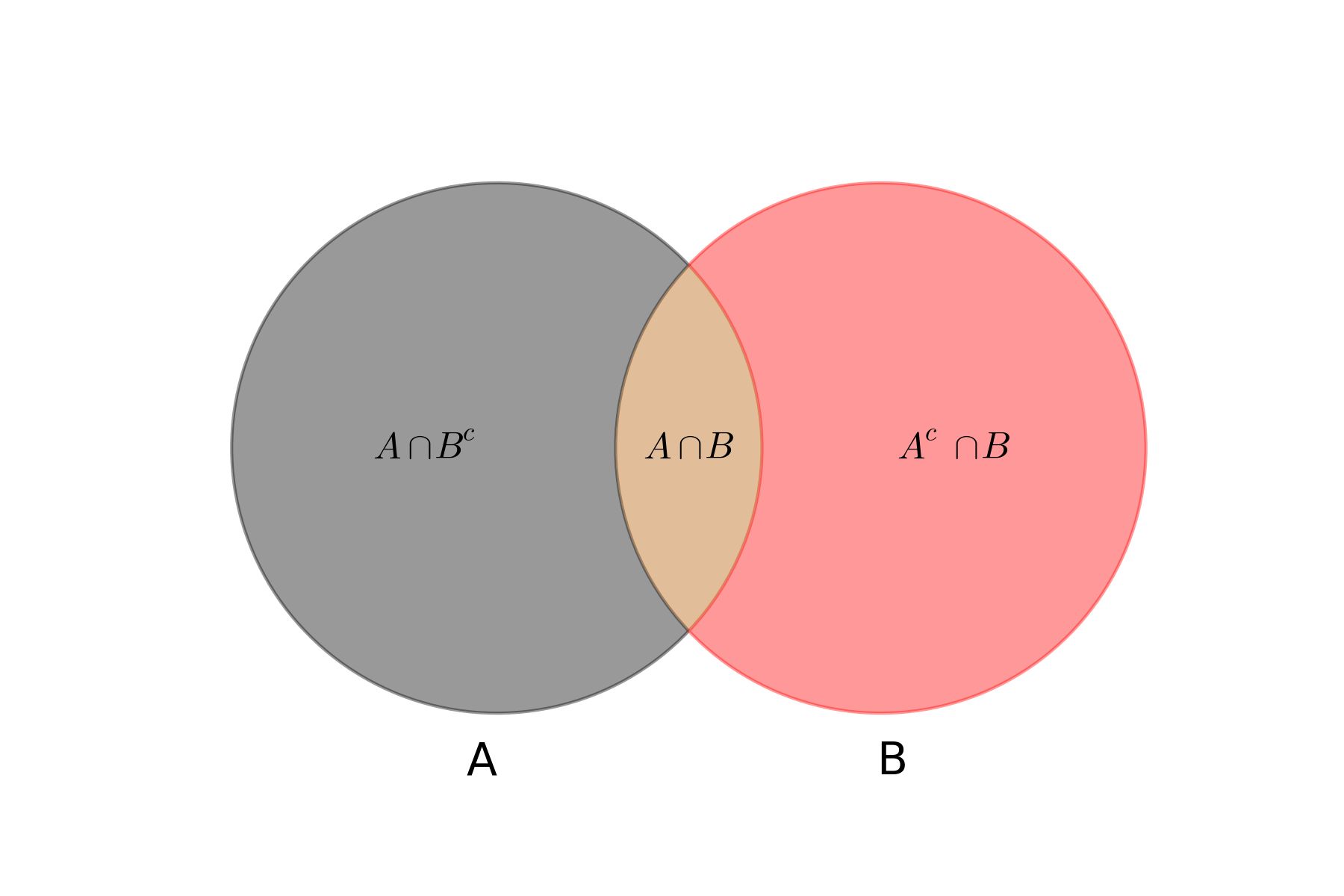
已知两个独立事件A和B，事件B发生的前提下，事件A发生的概率可以表示为P(A|B)，即上图中橙色部分占红色部分的比例，即:

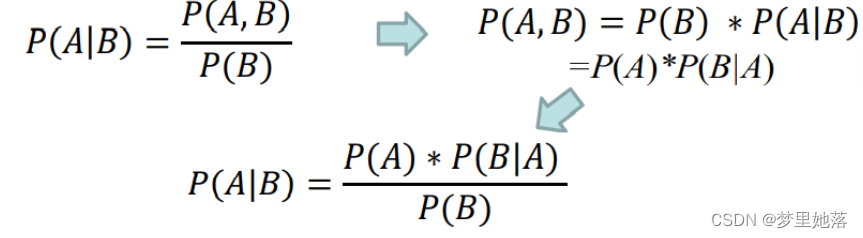
  • P(A) 称为”先验概率”，即在B事件发生之前，我们对A事件概率的一个判断。如：正常收到一封邮件，该邮件为垃圾邮件的概率就是“先验概率”

  • P(A|B)称为”后验概率”， 即在B事件发生之后，我们对A事件概率的重新评估。如：邮件中含有“中奖”这个词，该邮件为垃圾邮件的概率就是“后验概率”

  • P(B|A)/P(B)是可能性函数，这是一个调整因子，使得预估概率更接近真实概率。

  • 条件概率就是：后验概率　＝　先验概率 ｘ 调整因子

因为要计算两次概率，关于它们的分母，是这个样本的属性在全部样本中的概率。而这两次计算，它们的分母是不变的，所以我们只要计算分子就行。于是有了下面的结论：

即：

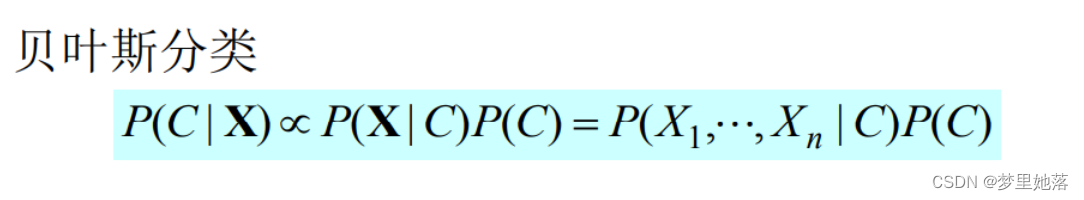
朴素贝叶斯分类器(Naïve Bayes Classifier)采用了“属性条件独立性假设”，即每个属性独立地对分类结果发生影响。为方便公式标记，不妨记P(C=c|X=x)为P(c|x)。在假设每个属性都独立的情况下，贝叶斯公式可以修改为：

分母是相同的，于是去掉分母，得：

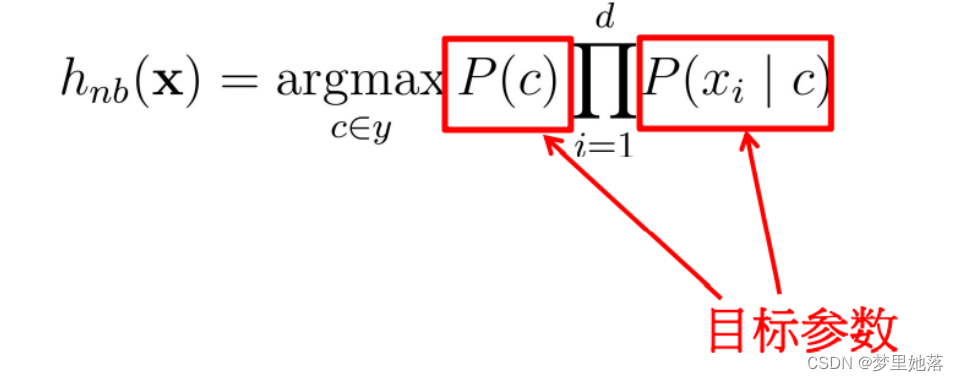
最终我们利用这个公式，在代码中实现概率的计算来对样本进行分类。

三、使用朴素贝叶斯进行垃圾邮件分类

1.算法思路

分类标准：当 P（垃圾邮件|文字内容）> P（正常邮件|文字内容）时，我们认为该邮件为垃圾邮件，但是单凭单个词而做出判断误差肯定相当大，因此我们可以将所有的词一起进行联合判断。假设我们进行判断的词语有“获奖”、“贷款”、“无利息”，则需要判断P（垃圾邮件|获奖，贷款，无利息）与P（正常|获奖，贷款，无利息），使用贝叶斯公式，P（垃圾邮件|获奖，贷款，无利息）可以变为：

假设所有词语独立同分布，可以得到

同理可得P（正常|获奖，贷款，无利息）

因此，对P（垃圾邮件|获奖，贷款，无利息）与P（正常|获奖，贷款，无利息）的比较，只需要对分子进行对比。

但是如果对多个词的P（内容|正常/垃圾）进行相乘时，可能会因为某个词的概率很小从而导致最后的结果为0（超出计算机的精度），因此可以对P（内容|正常/垃圾）取自然对数，即ln P（内容|正常/垃圾）。

因此可以变为

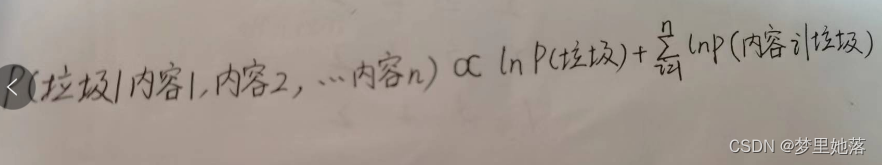
2.数据集准备

数据来源于国外的一些垃圾邮件和正常邮件

其中ham是正常邮件，spam是垃圾邮件。

3.数据导入

import os
import re
import string
import math

DATA_DIR = 'enron'
target_names = ['ham', 'spam']
def get_data(DATA_DIR):
    subfolders = ['enron%d' % i for i in range(1,7)] #获得enron下面的文件夹
    data = []
    target = []
    for subfolder in subfolders:
        #垃圾邮件 spam
        spam_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'spam')) #将文件夹路径进行组合
        for spam_file in spam_files: #遍历所有垃圾文件
            with open(os.path.join(DATA_DIR, subfolder, 'spam', spam_file), encoding="latin-1") as f:
                data.append(f.read())
                target.append(1)
        #正常邮件 pam
        ham_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'ham'))
        for ham_file in ham_files:
            with open(os.path.join(DATA_DIR, subfolder, 'ham', ham_file), encoding="latin-1") as f:
                data.append(f.read())
                target.append(0)
    return data, target
 
X, y = get_data(DATA_DIR)
#print(X,y)

邮件内容存储在data中，标签存储在target当中，“1”表示为垃圾邮件，“0”表示为正常邮件。下图为截取部分结果。

4.分析数据并进行算法训练

定义一个类对数据进行预处理

class SpamDetector_1(object):
    #清除空格
    def clean(self, s):
        translator = str.maketrans("", "", string.punctuation)
        return s.translate(translator)
    #分开每个单词
    def tokenize(self, text):
        text = self.clean(text).lower()
        return re.split("\W+", text)
    #计算某个单词出现的次数
    def get_word_counts(self, words):
        word_counts = {}
        for word in words:
            word_counts[word] = word_counts.get(word, 0.0) + 1.0
        return word_counts

计算P（垃圾邮件）和P（正常邮件）；词汇表（即正常邮件和垃圾邮件中出现的所有单词，方便进行拉普拉斯平滑）；垃圾邮件和非垃圾邮件的词频，即给定词在垃圾邮件和非垃圾邮件中出现的次数。选取了第100封之后的邮件作为训练集，前面一百封邮件作为测试集。

class SpamDetector_2(SpamDetector_1):
    # X:data,Y:target标签（垃圾邮件或正常邮件）
    def fit(self, X, Y):
        self.num_messages = {}
        self.log_class_priors = {}
        self.word_counts = {}
        # 建立一个集合存储所有出现的单词
        self.vocab = set()
        # 统计spam和ham邮件的个数
        self.num_messages['spam'] = sum(1 for label in Y if label == 1)
        self.num_messages['ham'] = sum(1 for label in Y if label == 0)
 
        # 计算先验概率，即所有的邮件中，垃圾邮件和正常邮件所占的比例
        self.log_class_priors['spam'] = math.log(
            self.num_messages['spam'] / (self.num_messages['spam'] + self.num_messages['ham']))
        self.log_class_priors['ham'] = math.log(
            self.num_messages['ham'] / (self.num_messages['spam'] + self.num_messages['ham']))
 
        self.word_counts['spam'] = {}
        self.word_counts['ham'] = {}
 
        for x, y in zip(X, Y):
            c = 'spam' if y == 1 else 'ham'
            # 构建一个字典存储单封邮件中的单词以及其个数
            counts = self.get_word_counts(self.tokenize(x))
            for word, count in counts.items():
                if word not in self.vocab:
                    self.vocab.add(word)#确保self.vocab中含有所有邮件中的单词
                # 下面语句是为了计算垃圾邮件和非垃圾邮件的词频，即给定词在垃圾邮件和非垃圾邮件中出现的次数。
                # c是0或1，垃圾邮件的标签
                if word not in self.word_counts[c]:
                    self.word_counts[c][word] = 0.0
                self.word_counts[c][word] += count
 
MNB = SpamDetector_2()
MNB.fit(X[100:], y[100:])

5.测试算法

对测试集进行测试，判断是垃圾邮件还是正常邮件，并计算出准确度

class SpamDetector(SpamDetector_2):
    def predict(self, X):
        result = []
        flag_1 = 0
        # 遍历所有的测试集
        for x in X:
            counts = self.get_word_counts(self.tokenize(x))  # 生成可以记录单词以及该单词出现的次数的字典
            spam_score = 0
            ham_score = 0
            flag_2 = 0
            for word, _ in counts.items():
                if word not in self.vocab: continue
 
                #下面计算P(内容|垃圾邮件)和P(内容|正常邮件),所有的单词都要进行拉普拉斯平滑
                else:
                    # 该单词存在于正常邮件的训练集和垃圾邮件的训练集当中
                    if word in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log(
                            (self.word_counts['spam'][word] + 1) / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log(
                            (self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
                                self.vocab)))
                    # 该单词存在于垃圾邮件的训练集当中,但不存在于正常邮件的训练集当中
                    if word in self.word_counts['spam'].keys() and word not in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log(
                            (self.word_counts['spam'][word] + 1) / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log( 1 / (sum(self.word_counts['ham'].values()) + len(
                                self.vocab)))
                    # 该单词存在于正常邮件的训练集当中,但不存在于垃圾邮件的训练集当中
                    if word not in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
                        log_w_given_spam = math.log( 1 / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
                        log_w_given_ham = math.log(
                            (self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
                                self.vocab)))
 
                # 把计算到的P(内容|垃圾邮件)和P(内容|正常邮件)加起来
                spam_score += log_w_given_spam
                ham_score += log_w_given_ham
 
                flag_2 += 1
 
                # 最后，还要把先验加上去，即P(垃圾邮件)和P(正常邮件)
                spam_score += self.log_class_priors['spam']
                ham_score += self.log_class_priors['ham']
 
            # 最后进行预测，如果spam_score > ham_score则标志为1，即垃圾邮件
            if spam_score > ham_score:
                result.append(1)
            else:
                result.append(0)
 
            flag_1 += 1
 
        return result

MNB = SpamDetector()
MNB.fit(X[100:], y[100:])
pred = MNB.predict(X[:100])
true = y[:100]
 
accuracy = 0
for i in range(100):
    if pred[i] == true[i]:
        accuracy += 1
print(accuracy)

最后得到准确率为99％

标签： 分类 人工智能
本文转载自: https://blog.csdn.net/jimei2011/article/details/128068976
版权归原作者 梦里她落 所有， 如有侵权，请联系我们删除。
登录后发布评论

“机器学习--使用朴素贝叶斯进行垃圾邮件分类”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

在 Git 中，获取提交的哈希值（commit hash）

Unity(2022.3.41LTS) - UI详细介绍- Panel(面板)和RectTransform组件

开源模型应用落地-Qwen2.5-7B-Instruct与TGI实现推理加速

简单的kafka&redis学习之redis

前端CryptoJS和Springboot后端(若依框架)数据互相加解密

uiotos、amis前端低代码对比

盘点SpringBoot中事务失效的十大场景

文章导航