机器学习之支持向量机（SVM）的求解方法

文章目录

前言

支持向量机就是寻找一个超平面，将不同的样本分分隔开来，其中间隔分为硬间隔和软间隔，硬间隔就是不允许样本分错，而软间隔就是允许一定程度上样本存在偏差，后者更符合实际。

支持向量机思路简单但是求解过程还是比较复杂，需要将原函数通过拉格朗日乘子法并附上KKT条件是的问题有强对偶性，再使用SMO等算法进行高效的求解。
推导过程可以参考：
机器学习之支持向量机之线性可分型原理介绍及代码实现（SVM）
下面主要实现模型的求解方法。

梯度下降法

梯度下降法是一种比较普适的方法，当模型无法得出解析解，或者解析解求解困难的时候，都可以使用梯度下降法来近似求解。因为梯度下降法需要一轮轮迭代，也需要定义损失函数，因此一般而言，梯度下降法只能获得近似最优解。
SVM可以使用梯度下降法求解，不过得出的解大概率只是近似解，并且不一定满足SVM的公式里的约束条件。

# coding=utf8import sys;import random;import numpy as np
import math

EPS =0.000000001# 很小的数字，用于判断浮点数是否等于0defload_data(filename, dim):'''
    输入数据格式: label\tindex1:value1\tindex2:value2\tindex3:value3..., 其中index是特征的编号, 从1开始
    data的数据格式: [[label, sample],[label, sample], ...],  其中sample: [v0, v1, v2, v3, ..., v[dim]]
    '''
    label_ =[]
    data_ =[]for line inopen(filename,'rt'):
        sample =[0.0for v inrange(0, dim +1)];
        line = line.rstrip("\r\n\t ");
        fields = line.split("\t");
        label =int(fields[0]);# LABEL取值: 1 or -1
        sample[0]=1.0;# sample第一个元素用于存x0特征, 默认置为1.0[方便把 WX+b => WX]for field in fields[1:]:
            kv = field.split(":");
            idx =int(kv[0]);# ensure idx >= 1
            val =float(kv[1]);
            sample[idx]= val;
        label_.append(label)
        data_.append(sample)
    
    label_ = np.array(label_)
    data_ = np.array(data_)return label_, data_
    

defsvm_train(train_x, train_y, dim, iterations, lm, lr):'''
    data4train:数据集
    dim:样本特征维度
    W:SVM模型的权重
    iterations:迭代次数
    目标函数: obj(<X,y>, W) = (对所有<X,y>SUM{max{0, 1 - W*X*y}}) + lm / 2 * ||W||^2, 即：hinge+L2
    '''
    X = np.zeros(dim +1)# <sample, label> => <X, y>
    grad = np.zeros(dim +1)# 梯度
    num_train =len(train_x);global W
    for i inrange(0, iterations):# 每次迭代随机选择一个训练样本
        index = random.randint(0, num_train -1);
        y = train_y[index]# y其实就是label
        X = train_x[index]# 计算梯度# for j in range(0, dim + 1):#    grad = lm * W[j];
        WX =0.0
        WX +=(W * X).sum()if1- WX * y >0:
            grad = lm * W - X * y
        else:# 1-WX *y <= 0的时候，目标函数的前半部分恒等于0, 梯度也是0
            grad = lm * W -0;# 更新权重, lr是学习速率
        W = W - lr * grad
        

defsvm_predict(x, y, dim, W):
    num_test =len(x);
    num_correct =0;for i inrange(0, num_test):
        target = y[i]# 即label
        X = x[i]# 即samplesum=0.0;sum+=(X * W).sum()
        predict =-1;# print sum;ifsum>0:# 权值>0，认为目标值为1
            predict =1;if predict * target >0:# 预测值和目标值符号相同
            num_correct +=1;return num_correct *1.0/ num_test;if __name__ =="__main__":# 设置参数
    epochs =10;# 迭代轮数
    iterations =10;# 每一轮中梯度下降迭代次数, 这个其实可以和epochs合并为一个参数
    lm =0.0001;# lambda, 对权值做正则化限制的权重
    lr =0.01;# lr, 是学习速率，用于调整训练收敛的速度
    dim =1000;# dim, 特征的最大维度, 所有样本不同特征总数
    W = np.zeros(dim +1)# 权值# 导入测试集&训练集
    train_y, train_x = load_data("train.txt", dim)
    test_y, test_x = load_data("test.txt", dim)# # 训练, 实际迭代次数=epochs * iterationsfor i inrange(0, epochs):
        svm_train(train_x, train_y, dim, iterations, lm, lr);
        accuracy = svm_predict(test_x, test_y, dim, W);print("epoch:%d\taccuracy:%f"%(i, accuracy));# 输出结果权值for i inrange(0, dim +1):if math.fabs(W[i])> EPS:print("权值W%d\t%f"%(i, W[i]));print(W)

这个是参考支持向量机SVM-手写笔记&手动实现这篇博客的，代码改成numpy进行运算了，进行改动的过程也是读懂代码的过程。

这个例子使用的梯度下降法，损失函数应该大概也许相当于用了max(0, x)。整体思路就是，每次就选一个样本点进行参数更新，如果这个样本点对于当前的参数能够正确分类，那么就不更新，如果不能正确分类，就更新。

运行结果如下：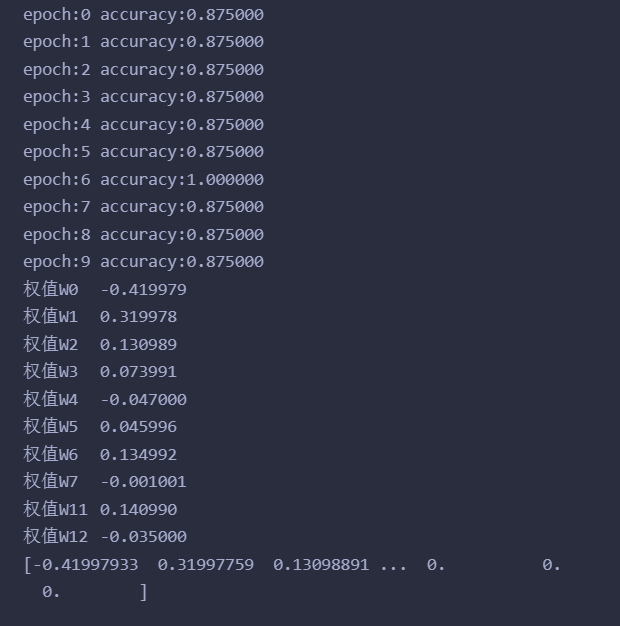

因为每次随机选择样本，那么其实找到的那个超平面大概率不会将样本集完全分开的，但是事实证明梯度下降法还是有效果的，所有，应该可以勉强认为训练出来的是软间隔的SVM吧？

SMO算法

贴上b站视频，以便日后再去看，实话说目前也没有完全走通这个算法的流程。
快速理解SMO算法
SMO算法思路很简单，因为存在约束条件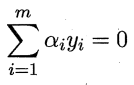

所以每次更新两个α，剩余看成常量，α能够通过看成的常量导出，然后满足约束条件的情况下求出极值，更新α。每次都更新两个，当固定其他的α时，能够求出选取α的更新的解析解，所以就算起来非常快。
那么该如何选择呢？
第一个αi应该选择违反KKT条件最大的。
第二个αj应该选择于第一个αi差值最大的。
这样能够保证每次更新都是向最快的方向进行更新。
思路是很简单，但是实践起来还是很困难的，因为里面涉及到许多的约束条件，不同情况下需要分类讨论等等。
直接贴上别人的代码吧

# -*- coding: utf-8 -*-from numpy import*import matplotlib.pyplot as plt
import random
defloadDataSet(filename): 
    dataMat=[]
    labelMat=[]
    fr=open(filename)for line in fr.readlines():
        lineArr=line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))return dataMat,labelMat 
classoptStruct:def__init__(self,dataMatIn, classLabels, C, toler):  
        self.X = dataMatIn  # 数据的特征
        self.labelMat = classLabels # 数据的标签
        self.C = C # 用于调整间隔大小
        self.tol = toler # 容错率
        self.m = shape(dataMatIn)[0]# 样本个数 
        self.alphas = mat(zeros((self.m,1)))# 需要求解的α
        self.b =0# 偏置
        self.eCache = mat(zeros((self.m,2)))# 第一列表示是否是个有效标志位，第二列存误差值Edefprint_m(self):print("self.X", self.X)print("self.labelMat", self.labelMat)print("self.C", self.C)print("self.tol", self.tol)print("self.m", self.m)print("self.alphas", self.alphas)print("self.b", self.b)print("self.eCache", self.eCache)# 随机选取一个J值defselectJrand(i,m): 
    j=i
    while(j==i):
        j=int(random.uniform(0,m))return j
 
# 根据关于α_1与α_2的优化问题对应的约束问题分析，对α进行截取约束# 保证取值范围符合约束条件 defclipAlpha(aj,H,L):if aj>H:
        aj=H
    if L>aj:
        aj=L
    return aj
        
#计算每个样本点k的Ek值，就是计算误差值=预测值-标签值        defcalcEk(oS, k): 
    fXk =float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)+ oS.b)
    Ek = fXk -float(oS.labelMat[k])return Ek
 

#内循环的启发式方法，获取最大差值|Ei-Ej|对应的Ej的索引JdefselectJ(i, oS, Ei):# 传入第一个α对应的索引i和误差值Ei

    maxK =-1#用于保存临时最大索引
    maxDeltaE =0#用于保存临时最大差值--->|Ei-Ej|
    Ej =0#保存我们需要的Ej误差值
    oS.eCache[i]=[1,Ei]# 获取有效误差的下标
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]if(len(validEcacheList))>1:# 如果存在符合条件的αjfor k in validEcacheList:if k == i:continue
            Ek = calcEk(oS, k)
            deltaE =abs(Ei - Ek)if(deltaE > maxDeltaE): 
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej # 找到与αi差值最大的αj(最优更新方向)else:# 不存在就任意选取
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)return j, Ej

# 更新EkdefupdateEk(oS, k): 
    Ek = calcEk(oS, k)
    oS.eCache[k]=[1,Ek]# 实现内循环函数definnerL(i, oS):# 确定了第一个αi# 计算出Ei
    Ei = calcEk(oS, i)# 如果违背了KKT条件if((oS.labelMat[i]*Ei <-oS.tol)and(oS.alphas[i]< oS.C))or((oS.labelMat[i]*Ei > oS.tol)and(oS.alphas[i]>0)):# 选择i对应确定的αj
        j,Ej = selectJ(i, oS, Ei)# 因为后面还需要用到原始值，因此需要记录下来
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()# 确定αj的取值范围if(oS.labelMat[i]!= oS.labelMat[j]):# 标签异号时
            L =max(0, oS.alphas[j]- oS.alphas[i])
            H =min(oS.C, oS.C + oS.alphas[j]- oS.alphas[i])else:# 标签同号
            L =max(0, oS.alphas[j]+ oS.alphas[i]- oS.C)
            H =min(oS.C, oS.alphas[j]+ oS.alphas[i])if L==H:print("L==H")return0# 2*xi*xj - xi^2 - xj^2 > 0 <=># xi^2 + xj^2 - 2xi*xj < 0  <=># （xi - xj）^2 < 0 <=># 没什么好算的  
        eta =2.0* oS.X[i,:]*oS.X[j,:].T-oS.X[i,:]*oS.X[i,:].T-oS.X[j,:]*oS.X[j,:].T
        if eta >=0:print("eta>=0")return0# 满足条件后更新αj
        oS.alphas[j]-= oS.labelMat[j]*(Ei - Ej)/eta 
        oS.alphas[j]= clipAlpha(oS.alphas[j],H,L)# 更新Ek 
        updateEk(oS, j)# 检测变化量是否显著if(abs(oS.alphas[j]- alphaJold)< oS.tol):print("j not moving enough")return0# αj 的变化量显著则更新 αi
        oS.alphas[i]+= oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])# 更新Ek
        updateEk(oS, i)# 更新b 
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        #根据统计学习方法中阈值b在每一步中都会进行更新，#1.当新值alpha_1不在界上时(0<alpha_1<C)，b_new的计算规则为：b_new=b1#2.当新值alpha_2不在界上时(0 < alpha_2 < C)，b_new的计算规则为：b_new = b2#3.否则当alpha_1和alpha_2都不在界上时，b_new = 1/2(b1+b2)if(0< oS.alphas[i]<oS.C):
            oS.b = b1
        elif(0< oS.alphas[j]<oS.C):
            oS.b = b2
        else:
            oS.b =(b1 + b2)/2.0# 更新完毕return1else:# 没有违反KKT条件return0# 根据西瓜书6.37计算W参数defcalcWs(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = array(alphas), array(dataMat), array(labelMat)
    w = dot((tile(labelMat.reshape(1,-1).T,(1,2))* dataMat).T, alphas)return w.tolist()defsmoP(dataMatIn, classLabels, C, toler, maxIter):# 初始化数据
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)# oS.print_m()iter=0# 当前迭代次数
    entireSet =True# 标志是否应该遍历整个数据集
    alphaPairsChanged =0# 标志一次循环中α更新的次数# 当迭代次数没有达到要求并且（有α被更新或者应该遍历整个数据集）则继续迭代while(iter< maxIter)and((alphaPairsChanged >0)or(entireSet)):
        alphaPairsChanged =0if entireSet:for i inrange(oS.m):
                alphaPairsChanged += innerL(i,oS)# innerL成功更新return 1print("fullSet, iter: %d i:%d, pairs changed %d"%(iter,i,alphaPairsChanged))iter+=1else:# 获取非边界值得索引
            nonBoundIs = nonzero((oS.alphas.A >0)*(oS.alphas.A < C))[0]for i in nonBoundIs: 
                alphaPairsChanged += innerL(i,oS)print("non-bound, iter: %d i:%d, pairs changed %d"%(iter,i,alphaPairsChanged))iter+=1# 实现交替遍历if entireSet:
            entireSet =Falseelif(alphaPairsChanged ==0): 
            entireSet =Trueprint("iteration number: %d"%iter)# oS.print_m()return oS.b,oS.alphas,oS
 
 
defshowClassifer(dataMat,labelMat,alphas, w, b):
    data_plus =[]                                  
    data_minus =[]for i inrange(len(dataMat)):if labelMat[i]>0:
            data_plus.append(dataMat[i])else:
            data_minus.append(dataMat[i])
    data_plus_np = array(data_plus)              
    data_minus_np = array(data_minus)            
    plt.scatter(transpose(data_plus_np)[0], transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(transpose(data_minus_np)[0], transpose(data_minus_np)[1], s=30, alpha=0.7) 
    x1 =max(dataMat)[0]
    x2 =min(dataMat)[0]
    a1, a2 = w
    b =float(b)
    a1 =float(a1[0])
    a2 =float(a2[0])
    y1, y2 =(-b- a1*x1)/a2,(-b - a1*x2)/a2
    plt.plot([x1, x2],[y1, y2])for i, alpha inenumerate(alphas):if0.6>abs(alpha)>0:
            x, y = dataMat[i]
            plt.scatter([x],[y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')if50==abs(alpha):
            x, y = dataMat[i]
            plt.scatter([x],[y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='yellow')
    plt.show()if __name__ =="__main__":
    x =[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49],[1.5,25],[3.5,45],[4.5,50],[6.5,15],[5.5,20],[5.8,74],[2.5,5]]
    y =[1,1,-1,-1,1,-1,-1,1,-1,-1,-1,1,1,-1,1]
    b, alphas, oS = smoP(dataMatIn=x,classLabels=y,C=50, toler=0.001,maxIter=400)
    w = calcWs(x,y,alphas)
    showClassifer(x,y,alphas, w, b)# oS.print_m() # 打印参数

运行结果：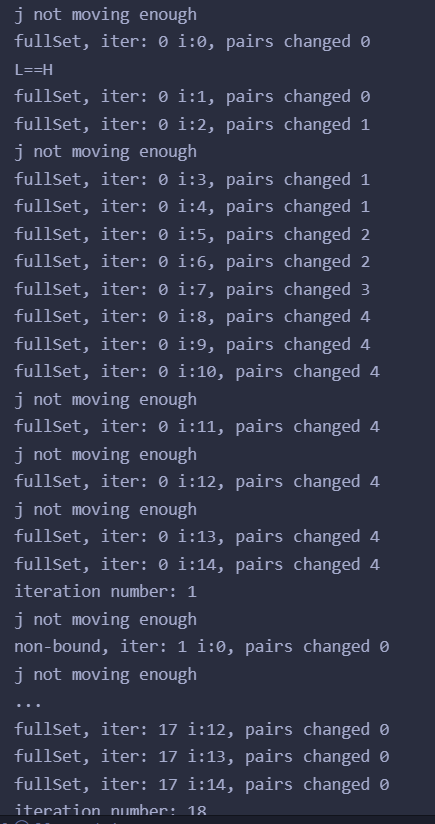


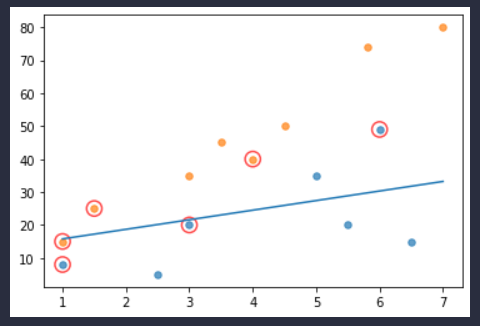
其中画圈的就是支持向量机的支持向量，也就是α不为0的样本是对超平面位置有影响的样本点。

SMO算法实现细节可能还是没完全明白，以后懂了再来补吧。

参考

支持向量机SVM-手写笔记&手动实现
https://www.cnblogs.com/ssyfj/p/13363526.html
SVM SMO算法代码详细剖析