机器学习之聚类——从教授的等式到凸聚类

​
​

活动地址：CSDN21天学习挑战赛

引子：大佬的等式

在美国，有个牛逼的大学，叫华盛顿大学，其中有个牛逼的计算机科学教授，佩德罗·多明戈斯（Pedro Domingos），他是《终极算法》的作者，还有很多著作和头衔，不过，今天我们关注的不是这些著作和头衔，而是他写过的一个著名的方程式：

机器学习=表示+优化+评估

上面的等式说明了优化是机器学习中十分关键的部分，本文就优化部分做一些讨论

凸优化和非凸优化的区别

    总的来说，凸优化和非凸优化的最大的区别在它们的目标函数及其可行域，凸优化问题的目标函数在其可行域内有一个特别优良的性质：局部最优解便是全局最优解。而非凸优化则不然，它在可行域内有多个局部最优解，求解其全局最优解则比较困难。
     机器学习优化中，常用的迭代算法如梯度下降法、牛顿法都比较容易得到局部最优解，而对于非凸优化的全局最优解，则难以稳定的求解。所以，人们更喜欢凸优化问题。
     构造完凸优化问题后，求解过程大致分为两部分，构造对偶问题，然后求解对偶问题从而获得原问题的解。

凸聚类

     将凸优化和聚类问题相结合，便构成了凸聚类问题。
     可以用矩阵的语言描述聚类问题，如下：

    显然，这两个目标是相互冲突的，因此任何一种聚类算法都希望在最大化类间距离和最小化类内距离之间取一个平衡点，故而诞生了不同的聚类算法。
     无论是k-means算法还是谱聚类算法，本质都是一个非凸问题，这使得问题的解受初始值的影响很大。虽然人们已经提出了很多不同的初始化算法来提升聚类性能，但至今都没有一种最优的初始化策略出现。通过将聚类问题描述为一个凸优化问题，凸聚类算法通过凸优化算法获得聚类问题的唯一解，从而避免初始值的选取对聚类结果的影响。

     上面目标函数的第一项为矩阵U与X之差的Frobenius范数，用来控制矩阵U与X的距离，第二项为矩阵U内部不同列之间距离的加权和，用来控制矩阵U内部不同列之间的距离。可以预见，能够目标函数最小的矩阵U可以使U与X接近的同时使U内列向量之间距离较小。在凸聚类算法处理后，U内部同属于一个聚类的向量距离会变小，而不属于同一个聚类的向量虽然距离也可能会变小，但是幅度不大，使得U内部的聚类模式体现得更加明显，之后只需要对矩阵U使用非常简单的聚类算法（比如k-means等），就可以获得U中列向量的聚类，它们也就对应了X中列向量的聚类。在实践中，一般使用直接比较U列向量之间距离的方法来确定聚类个数和每一个列向量所属的聚类。
     凸聚类算法试图绕过初始化问题，直接针对聚类问题设计出一个凸的目标函数，从而仅仅通过非常简单的算法就能求得全局最优解。通过连续可调的参数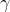![\gamma](https://latex.codecogs.com/gif.latex?%5Cgamma)，凸聚类算法可以生成数目不等的聚类，从而实现对聚类个数k的间接控制。

作者这水平有限，有不足之处欢迎留言指正

​