1. 多重共线性
** 多重共线性**是指**线性回归模型**中的解释变量之间由于存在精确或高度**相关关系**。
例如：某个回归模型包含2个变量，**年龄**和**工作经验年数**，常识可知年龄越大，工作经验年数越大，两个变量可能存在**高度关联**，因此模型中可能存在**多重共线性**。
2. 多重共线性的危害
a. **模型估计失真** 或 **难以估计准确 **或 **稳定性降低**，意味着回归方程的标准误差可能会增大；
b. 模型**参数估计不准确**，方差大，这也是模型估计不准的原进一步原因，至于为什么看3
c. 无法判断单独变量的影响，计算特征贡献度；
d. 因此自**变量显著性**可能会失去意义，本应该显著的自变量不显著，本不显著的自变量却是显著
3. 共线性的存在导致模型估计不准的原因
最小化损失函数的目的是找到一组**最优回归系数**，宏观定义上可以理解为模型参数。多重共线性的存在会导致**模型参数估计不准确**，进而**导致模型估计失真** 或 **估计不准的问题**。
简单穿插一下回归系数的概念：
回归系数：regression coefficient
回归系数在 回归方程 中表示 自变量 x 对 因变量 y 影响大小的**参数，**它反映当自变量每**变化一个单位**时，因变量所**期望的变化量**。 回归系数越大表示 x 对 y 的影响越大，**正回归系数**表示 y 随 x 增大而增大，**负回归系数**表示 y 随 x 增大而减小。 例如回归方程式Y=bX+a中，斜率 b称为回归系数，表示X每变动一单位，平均而言，Y将变动b单位。更通俗的讲：从线性回归的角度进一步理解回归系数。
变量** y **与变量 **x = (x1, x2, x3.....,xn)**，之间的关系是 ，此时称 f(x) 为 y 对 x 的回归，f(x) 称为回归函数。通常在正态分布情形，若 f(x) 是 x 的线性函数 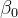，是回归常数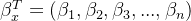， 称为**回归系数**。
回到多重共线性的危害上：
如果模型中存在多重共线性，这说明至少有两个自变量 A 和 B 是**高度或完全相关**的，即两个变量的变化趋势一致，其中一个变化，另一个也会发生类似的变化。相关性越强，在只改变A，不改变B的情况下，**单纯从A的变化解释Y的变化就很困难**，也就是和实际不符（实际环境可能是从A和B共同变化的角度解释Y的变化，因此很难理解）。
因此，会降低估计系数的可信度 或者 降低模型 的稳定性和性能。
4. 判断标准
a. **皮尔逊相关系数**，可以解释连续型变量之间的线性相关程度，该值大于0.8，则可以认为存在多重共线性；对于连续型—离散型和离散型—离散型的变量对，则可以利用其他的方式（后续会另开一篇）；
b. 实现增加一个变量或者删除一个变量，观察回归系数的值是否有很大变化，若变化很大，则说明该变量的估计系数不可信 或 不稳定；
c. 如果说 F 检验通过，并且决定系数值也较大，但是 t 检验并不显著，也可能存在多重共线性；
d. 回归系数的正负符号与专业知识相反或与实际分析结果不符，也会存在多重共线性的可能。
以上a ~ d，均为主观判断方法；还有一种正规的检验方法！
观察回归分析中的**VIF值**（方差膨胀因子），表达式1 / (1 - r2)。多重共线性会使参数估计值的方差变大，方差膨胀因子越大，说明共线性越强。通常的判断标准是**VIF值**大于10，即具有多重共线性，有的文献也说大于5即有共线性。
5. 解决办法，如何消除多重共线性
a. 保留一个变量，并删除与其高度相关的其他变量，以**逐步回归法**得到最广泛的应用；
b. 引入L1 和 L2 正则化，减少参数量的方差，降低VIF，可以处理多重共线性；
c.** 特征合并**或者**特征组合**，将相关变量线性组合在一起处理；
d. 特征降维，如PCA
e. 差分法，时间序列数据、线性模型：将原模型变换为差分模型（转自百度百科，我没懂。。）
上述内容源自：回归系数_百度百科，多重共线性_百度百科，速进！！关于多重共线性你知道多少？ - 知乎 以及 自己的学习和理解，可以的话，这几篇都可以看看。
本文转载自: https://blog.csdn.net/xiao_ling_yun/article/details/129571018
版权归原作者 云从天上来 所有， 如有侵权，请联系我们删除。
版权归原作者 云从天上来 所有， 如有侵权，请联系我们删除。