paper：Denoising Diffusion Probabilistic Models（https://arxiv.org/abs/2006.11239）
本文代码地址：pytorch cifar10：https://github.com/w86763777/pytorch-ddpm
一、超参数设置【main.py】
超参数设置使用absl包中flags进行管理，
–num_res_blocks是Unet中每个level的resnet数量，
–attn是attention block，向这些层中添加注意力，
这个是后面我们加入condition的途径，非常重要。
flags.DEFINE_multi_integer('attn',[1],help='add attention to these levels')
flags.DEFINE_integer('num_res_blocks',2,help='# resblock in each level')
这里通过“pip install absl-py”就可以安装absl，然后通过“from absl import app, flags”，FLAGS = flags.FLAGS
flags.DEFINE_bool(‘train’, False, help=‘train from scratch’)就可以使用了
–beta_1,–beta_T对应于
β
1
\beta_1
β1和
β
T
\beta_T
βT，实际的
β
t
\beta_t
βt是在
β
1
\beta_1
β1,
β
T
\beta_T
βT中线性采样得到的。DDPM原文中研究了是否固定
β
t
\beta_t
βt对实验结果的影响，后面很多论文也做了对比实验探索是否
β
\beta
β线性增长对实验效果的影响。
T是采样的步长，这个对采样质量和生成时间影响非常大。T越大，采样时间越长，3060Ti显卡采样一个batch的数据设置需要20小时。但是T越大并不是质量越高，呈二次函数关系。（随着T增大，生成质量先变好再变差）
flags.DEFINE_float('beta_1',1e-4,help='start beta value')
flags.DEFINE_float('beta_T',0.02,help='end beta value')
flags.DEFINE_integer('T',1000,help='total diffusion steps')
–image_size根据数据集实际情况设置，这是影响生成时间的重要因素，size和时间呈指数倍爆炸增长。
flags.DEFINE_integer('img_size',32,help='image size')
二、训练CIFAR10数据集的配置信息【config/CIFAR10.txt】
由于不同的数据集unet channel、T、image size等关键参数是不一样的，因此针对不同的数据集用不同的txt文件进行管理。
--T=1000--attn=1--batch_size=128--beta_1=0.0001--beta_T=0.02--ch=128--ch_mult=1--ch_mult=2--ch_mult=2--ch_mult=2--dropout=0.1--ema_decay=0.9999--noeval
--eval_step=0--fid_cache=./stats/cifar10.train.npz
--nofid_use_torch
--grad_clip=1.0--img_size=32--logdir=./logs/DDPM_CIFAR10_EPS
--lr=0.0002--mean_type=epsilon
--num_images=50000--num_res_blocks=2--num_workers=4--noparallel
--sample_size=64--sample_step=1000--save_step=5000--total_steps=800000--train
--var_type=fixedlarge
--warmup=5000
1）加载数据集【main.py】
以加载cifar10数据集为例：
# dataset
dataset = CIFAR10(
root='./data', train=True, download=True,
transform=transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5)),]))
dataloader = torch.utils.data.DataLoader(
dataset, batch_size=FLAGS.batch_size, shuffle=True, num_workers=FLAGS.num_workers, drop_last=True)
datalooper = infiniteloop(dataloader)
每个loop使用next()方法即可加载输入的图像
x
0
x_0
x0：
x_0 =next(datalooper).to(device)
三、loss计算【diffusion.py】
原文的loss计算公式：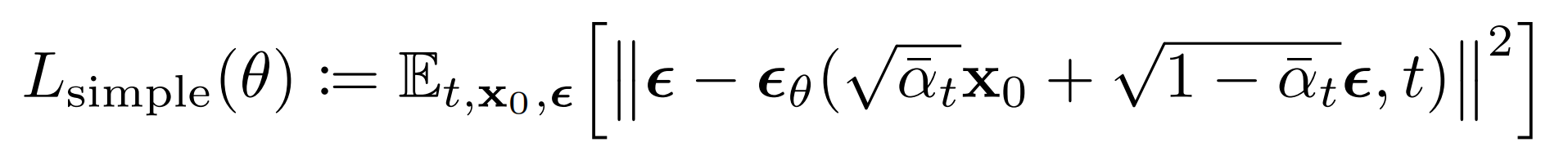
计算的是纯噪声noise
ϵ
\epsilon
ϵ 和
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
,
t
)
\boldsymbol{\epsilon}_{\theta}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}, t\right)
ϵθ(αˉtx0+1−αˉtϵ,t)之间的损失（均方差）：【因为噪声
ϵ
θ
\boldsymbol{\epsilon}_{\theta}
ϵθ可以通过
x
t
x_t
xt 以及 时间步
t
t
t 计算得出，所以这里输入进model的是x_t 和 t】，其中noise
ϵ
\epsilon
ϵ 的size和输入的图像 x_0 是一样的：
noise = torch.randn_like(x_0)
loss = F.mse_loss(self.model(x_t, t), noise, reduction='none')
因为要计算它们之间的损失，为了计算出noise
ϵ
θ
\boldsymbol{\epsilon}_{\theta}
ϵθ，所以需要求出
x
t
x_t
xt，也就是（x_t）
1）计算
α
ˉ
t
\bar{\alpha}_{t}
αˉt，
α
ˉ
t
\sqrt{\bar{\alpha}_{t}}
αˉt，
1
−
α
ˉ
t
\sqrt{1-\bar{\alpha}_{t}}
1−αˉt，从而根据公式得到
x
t
x_t
xt
**1、根据
β
1
\beta_1
β1和
β
T
\beta_T
βT计算所有的
β
t
\beta_t
βt**
DDPM原始的论文设置的是线性增长，后面不少文章设置了指数增长等其他方式，只要满足足够小假设即可。
self.register_buffer('betas', torch.linspace(beta_1, beta_T, T).double())
**2、计算
α
t
\alpha_t
αt**
α
t
=
1
−
β
t
\alpha_t = 1 - \beta_t
αt=1−βt
alphas =1.- self.betas
**3、累乘得到
α
ˉ
t
\bar{\alpha}_{t}
αˉt**
alphas_bar = torch.cumprod(alphas, dim=0)
最后将这些一同写入buffer即可：
sqrt_alphas_bar =
α
ˉ
t
\sqrt{\bar{\alpha}_{t}}
αˉt，
sqrt_one_minus_alphas_bar =
1
−
α
ˉ
t
\sqrt{1-\bar{\alpha}_{t}}
1−αˉt
self.register_buffer('sqrt_alphas_bar', torch.sqrt(alphas_bar))
self.register_buffer('sqrt_one_minus_alphas_bar', torch.sqrt(1.- alphas_bar))
2）根据
α
ˉ
t
\bar{\alpha}_{t}
αˉt，
α
ˉ
t
\sqrt{\bar{\alpha}_{t}}
αˉt，
1
−
α
ˉ
t
\sqrt{1-\bar{\alpha}_{t}}
1−αˉt，从而根据公式得到forward过程中的
x
t
x_t
xt
x
t
x_t
xt的具体的计算公式如下：
x
t
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
x_t = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}
xt=αˉtx0+1−αˉtϵ
其中时刻信息 t 是通过
α
ˉ
t
\bar{\alpha}_{t}
αˉt 表现的。不难写出计算代码，其中extract函数的作用是选取特定下标 t 的参数信息并转换成特定维度用于广播。：
# 其中v是sqrt_alphas_bar、sqrt_one_minus_alphas_bar这种，t是时间步，x_shape是x的维度# 其中extract函数的作用是：将alphas这种转为特定时间步t下的alphasdefextract(v, t, x_shape):"""
Extract some coefficients at specified timesteps, then reshape to [batch_size, 1, 1, 1, 1, ...] for broadcasting purposes.
"""
out = torch.gather(v, index=t, dim=0).float()return out.view([t.shape[0]]+[1]*(len(x_shape)-1))
计算得到
x
t
x_t
xt
x_t =(extract(self.sqrt_alphas_bar, t, x_0.shape)* x_0 +
extract(self.sqrt_one_minus_alphas_bar, t, x_0.shape)* noise)
计算
1
−
α
t
ˉ
1
−
α
ˉ
t
\frac{1-\bar{\alpha_{t}}}{\sqrt{1-\bar{\alpha}_{t}}}
1−αˉt
1−αtˉ
# below: log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
self.register_buffer('posterior_log_var_clipped', torch.log(torch.cat([self.posterior_var[1:2], self.posterior_var[1:]])))
self.register_buffer('posterior_mean_coef1', torch.sqrt(alphas_bar_prev)* self.betas /(1.- alphas_bar))
self.register_buffer('posterior_mean_coef2', torch.sqrt(alphas)*(1.- alphas_bar_prev)/(1.- alphas_bar))
defpredict_xstart_from_xprev(self, x_t, t, xprev):assert x_t.shape == xprev.shape
# (xprev - coef2*x_t) / coef1return(
extract(1./ self.posterior_mean_coef1, t, x_t.shape)* xprev -
extract(self.posterior_mean_coef2 / self.posterior_mean_coef1, t, x_t.shape)* x_t
)
本文转载自: https://blog.csdn.net/weixin_43135178/article/details/127967417
版权归原作者 HealthScience 所有， 如有侵权，请联系我们删除。
版权归原作者 HealthScience 所有， 如有侵权，请联系我们删除。