机器学习5—分类算法之随机森林（Random Forest）

随机森林（Random Forest）

前言

随机森林（Random Forest） 是Bagging（一种并行式的集成学习方法）的一个拓展体，它的基学习器固定为决策树，多棵树也就组成了森林，而“随机”则在于选择划分属性的随机，随机森林在训练基学习器时，也采用有放回采样的方式添加样本扰动，同时它还引入了一种属性扰动，即在基决策树的训练过程中，在选择划分属性时，Random Forest先从候选属性集中随机挑选出一个包含K个属性的子集，再从这个子集中选择最优划分属性，一般推荐K=log2（d）。

这样随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动，从而进一步提升了基学习器之间的差异度。
相比决策树的Bagging集成，随机森林的起始性能较差（由于属性扰动，基决策树的准确度有所下降），但随着基学
习器数目的增多，随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划
分属性，随机森林只在属性集的一个子集中选择划分属性，因此训练效率更高。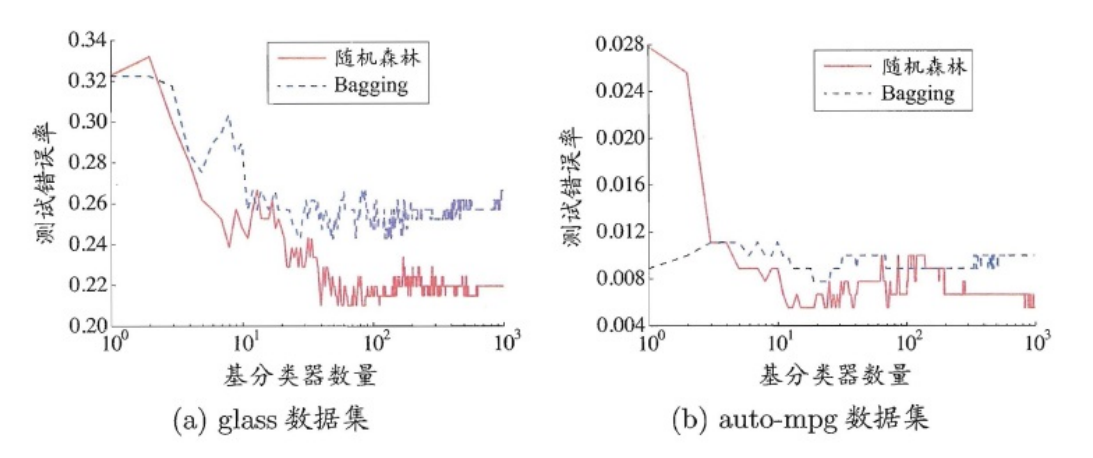

提示：以下是本篇文章正文内容，下面案例可供参考

一、随机森林

1.什么是随机森林

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。“森林”我们很好理解，一棵叫做树，那么成百上千棵就可以叫做森林了，这样的比喻还是很贴切的，其实这也是随机森林的主要思想–集成思想的体现。

从直观角度来解释，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。

2.随机森林的特点

• 随机森林主页：Random Forest。

随机森林的优缺点

优点：

• 1） 每棵树都选择部分样本及部分特征，一定程度避免过拟合；
• 2） 每棵树随机选择样本并随机选择特征，使得具有很好的抗噪能力，性能稳定；
• 3） 能处理很高维度的数据，并且不用做特征选择（不需要降维处理）；
• 4） 适合并行计算；
• 5） 实现比较简单。

缺点：

• 1） 参数较复杂；
• 2） 模型训练和预测都比较慢。

3.随机森林的生成

随机森林中有许多的分类树。我们要将一个输入样本进行分类，我们需要将输入样本输入到每棵树中进行分类。打个形象的比喻：森林中召开会议，讨论某个动物到底是老鼠还是松鼠，每棵树都要独立地发表自己对这个问题的看法，也就是每棵树都要投票。该动物到底是老鼠还是松鼠，要依据投票情况来确定，获得票数最多的类别就是森林的分类结果。森林中的每棵树都是独立的，99.9%不相关的树做出的预测结果涵盖所有的情况，这些预测结果将会彼此抵消。少数优秀的树的预测结果将会超脱于芸芸“噪音”，做出一个好的预测。将若干个弱分类器的分类结果进行投票选择，从而组成一个强分类器，这就是随机森林bagging的思想（关于bagging的一个有必要提及的问题：bagging的代价是不用单棵决策树来做预测，具体哪个变量起到重要作用变得未知，所以bagging改进了预测准确率但损失了解释性。）。下图可以形象地描述这个情况：

森林中树的生成规则为：

• 1）如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本（这种采样方式称为bootstrap sample方法），作为该树的训练集；

每棵树的训练集都是不同的，而且里面包含重复的训练样本。

• 为什么要随机抽样训练集：如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的，这样的话完全没有bagging的必要；
• 为什么要有放回地抽样：如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是"有偏的"，都是绝对"片面的"，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决，这种表决应该是"求同"，所以说使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的，这样无异于是"盲人摸象"。

• 2）如果每个样本的特征维度为M，指定一个常数m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这m个特征中选择最优的；
• 3）每棵树都尽最大程度的生长，并且没有剪枝过程。

随机森林分类效果（错误率）与两个因素有关：

• 森林中任意两棵树的相关性：相关性越大，则错误率越大；
• 森林中每棵树的分类能力：每棵树的分类能力越强，则整个森林的错误率就越低。

则随机森林有着：减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数。

二、随机森林的函数模型

在sklearn机器模型中，Radom Forest函数为：

RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None,
                       min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
                       max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0,
                       min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=1,
                       random_state=None,verbose=0, warm_start=False, class_weight=None)

参数作用：

n_estimators:数值型取值
    含义：森林中决策树的个数，默认是10
    
criterion:字符型取值
    含义：采用何种方法度量分裂质量，信息熵或者基尼指数，默认是基尼指数

max_features:取值为int型, float型, string类型, or None()，默认"auto"
    含义：寻求最佳分割时的考虑的特征数量，即特征数达到多大时进行分割。
    int:max_features等于这个int值
    float:max_features是一个百分比，每(max_features * n_features)特征在每个分割出被考虑。
    "auto":max_features等于sqrt(n_features)
    "sqrt":同等于"auto"时
    "log2":max_features=log2(n_features)
    None:max_features = n_features

max_depth:int型取值或者None，默认为None
    含义：树的最大深度

min_samples_split:int型取值，float型取值，默认为2
    含义：分割内部节点所需的最少样本数量
    int:如果是int值，则就是这个int值
    float:如果是float值，则为min_samples_split * n_samples

min_samples_leaf:int取值，float取值，默认为1
    含义：叶子节点上包含的样本最小值
    int:就是这个int值
    float:min_samples_leaf * n_samples

min_weight_fraction_leaf : float，default=0.
    含义：能成为叶子节点的条件是：该节点对应的实例数和总样本数的比值，至少大于这个min_weight_fraction_leaf值

max_leaf_nodes:int类型，或者None(默认None)
    含义：最大叶子节点数，以最好的优先方式生成树，最好的节点被定义为杂质相对较少，即纯度较高的叶子节点

min_impurity_split:float取值 
    含义：树增长停止的阀值。一个节点将会分裂，如果他的杂质度比这个阀值；如果比这个值低，就会成为一个叶子节点。

min_impurity_decrease:float取值，默认0.
    含义：一个节点将会被分裂，如果分裂之后，杂质度的减少效果高于这个值。

bootstrap:boolean类型取值，默认True
    含义：是否采用有放回式的抽样方式

oob_score:boolean类型取值，默认False
    含义：是否使用袋外样本来估计该模型大概的准确率

n_jobs:int类型取值，默认1
    含义：拟合和预测过程中并行运用的作业数量。如果为-1，则作业数设置为处理器的core数。

class_weight:dict, list or dicts, "balanced"
    含义：如果没有给定这个值，那么所有类别都应该是权重1
    对于多分类问题，可以按照分类结果y的可能取值的顺序给出一个list或者dict值，用来指明各类的权重.
    "balanced"模式，使用y值自动调整权重，该模式类别权重与输入数据中的类别频率成反比，即n_samples / (n_classes * np.bincount(y))，分布为第n个类别对应的实例数。
    "balanced_subsample"模式和"balanced"模式类似，只是它计算使用的是有放回式的取样中取得样本数，而不是总样本数

三、随机森林算法实现

数据集下载：https://www.kaggle.com/c/titanic/data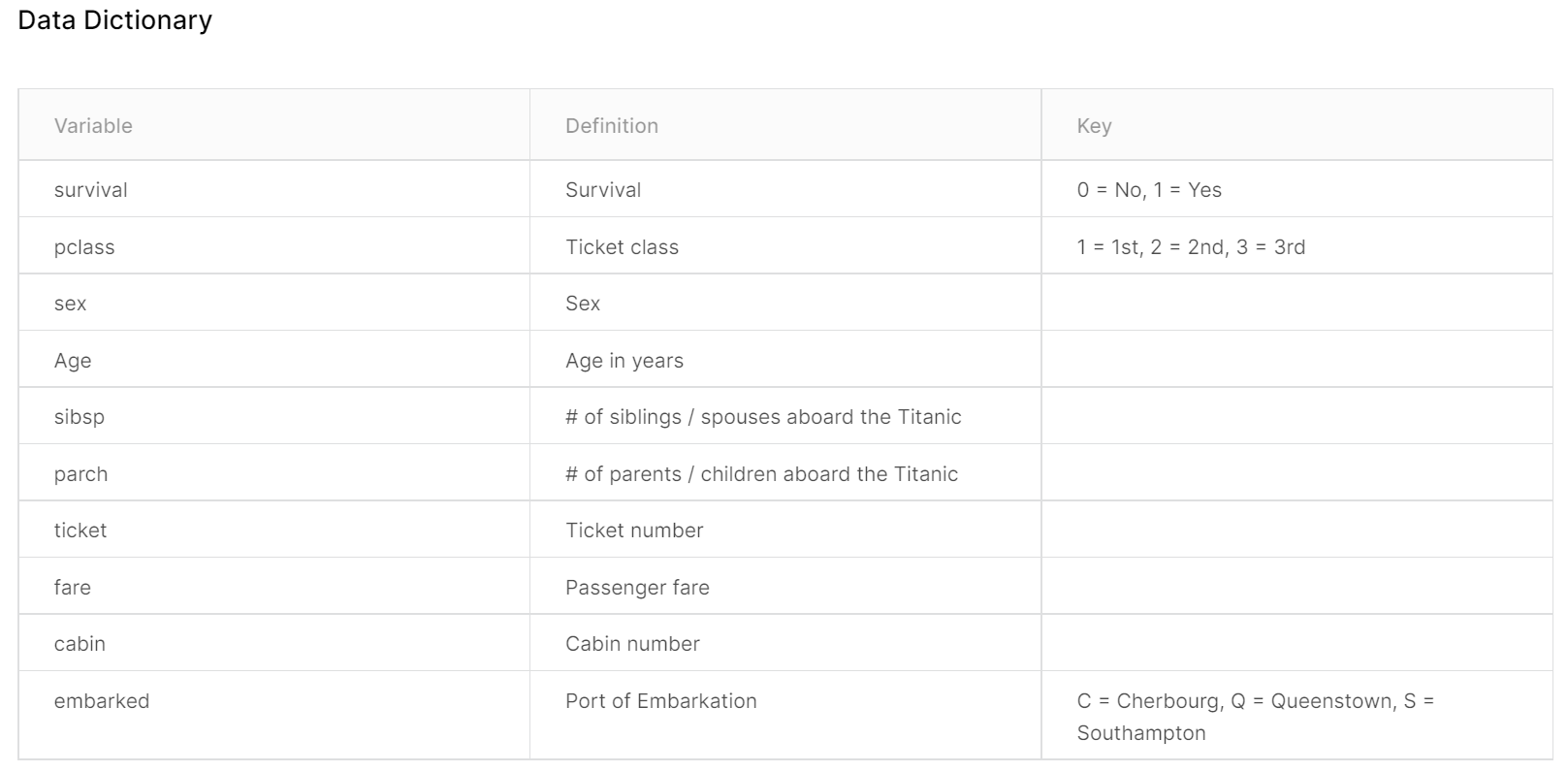

上面的一张图，是我从官网上下载的，总的来说，里面的每一行数据，差不多有11个字段，包括游客的年龄、名字、性别、买的几等仓的票等等信息，最后是他的生存情况，在这场事故中，他是死了还是幸存。

1.数据的读取

对前10行数据的读取

import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
train = pd.read_csv("train.csv", dtype={"Age": np.float64},)
train.head(10)

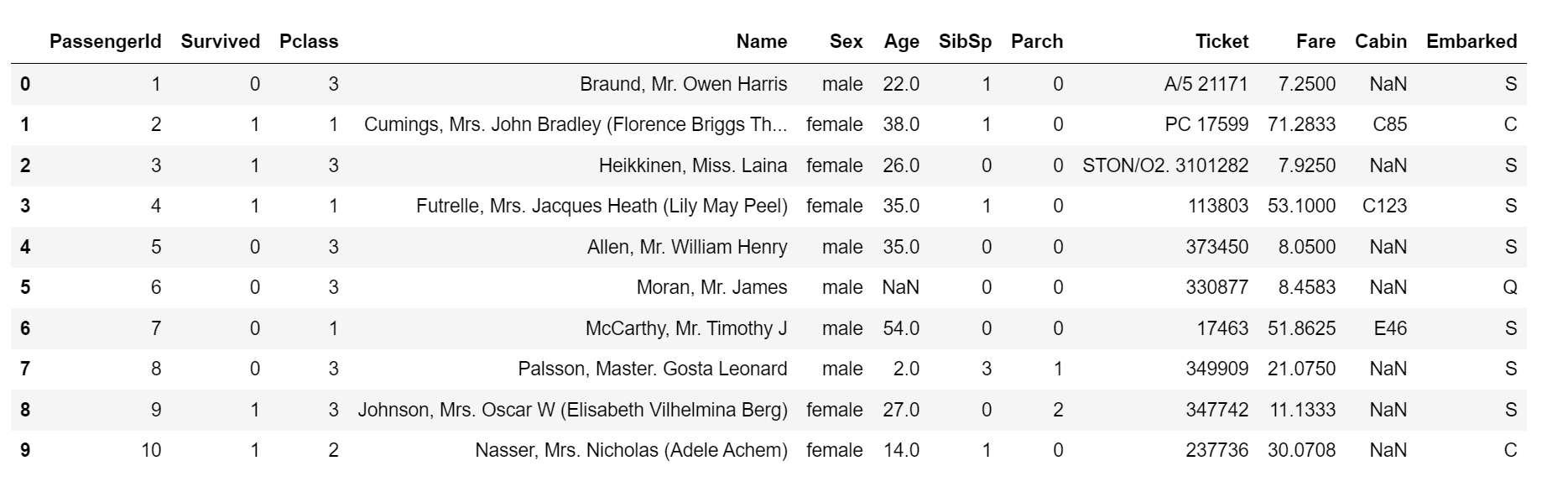
稍微分析一下，我们就可以筛选出对一个游客的生存与否有关的变量：Pclass, Sex, Age, SibSp，Parch，Fare, Embarked. 一般来说，游客的名字，买的船票号码对其的生存情况应该影响很小。

print(len(train_data))
out:891

2.数据的清洗和填充

在sklearn自带的随机森林算法中，输入的值必须是整数或者浮点数，所以我们需要对数据进行预处理，将字符串转化成整数或者浮点数：

defharmonize_data(titanic):# 填充空数据 和 把string数据转成integer表示# 对于年龄字段发生缺失，我们用所有年龄的均值替代
    titanic["Age"]= titanic["Age"].fillna(titanic["Age"].median())# fillna方法来将缺失值替换成常值# 性别男： 用0替代
    titanic.loc[titanic["Sex"]=="male","Sex"]=0# 性别女： 用1替代
    titanic.loc[titanic["Sex"]=="female","Sex"]=1

    titanic["Embarked"]= titanic["Embarked"].fillna("S")# 将列Embarked中出现的S、C、Q用0、1、2来代替
    titanic.loc[titanic["Embarked"]=="S","Embarked"]=0
    titanic.loc[titanic["Embarked"]=="C","Embarked"]=1
    titanic.loc[titanic["Embarked"]=="Q","Embarked"]=2

    titanic["Fare"]= titanic["Fare"].fillna(titanic["Fare"].median())return titanic

train_data = harmonize_data(train)

上面的代码是对原始数据进行清洗，填补缺失数据， 把string类型数据转化成int数据

3.数据的划分

数据划分为训练数据和测试数据，总的数据有891个，我们用600个训练数据集，剩下的291个作为测试数据集。

# 列出对生存结果有影响的字段
predictors =["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked"]# 存放不同参数取值，以及对应的精度，每一个元素都是一个三元组(a, b, c)
results =[]# 最小叶子结点的参数取值
sample_leaf_options =list(range(1,500,3))# 决策树个数参数取值
n_estimators_options =list(range(1,1000,5))
groud_truth = train_data['Survived'][601:]for leaf_size in sample_leaf_options:for n_estimators_size in n_estimators_options:
        alg = RandomForestClassifier(min_samples_leaf=leaf_size, n_estimators=n_estimators_size, random_state=50)
        alg.fit(train_data[predictors][:600], train_data['Survived'][:600])
        predict = alg.predict(train_data[predictors][601:])# 用一个三元组，分别记录当前的 min_samples_leaf，n_estimators， 和在测试数据集上的精度
        results.append((leaf_size, n_estimators_size,(groud_truth == predict).mean()))# 真实结果和预测结果进行比较，计算准确率print((groud_truth == predict).mean())# 打印精度最大的那一个三元组print(max(results, key=lambda x: x[2]))

4.代码的实现

import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier

train = pd.read_csv("train.csv", dtype={"Age": np.float64},)defharmonize_data(titanic):# 填充空数据 和 把string数据转成integer表示

    titanic["Age"]= titanic["Age"].fillna(titanic["Age"].median())

    titanic.loc[titanic["Sex"]=="male","Sex"]=0
    titanic.loc[titanic["Sex"]=="female","Sex"]=1

    titanic["Embarked"]= titanic["Embarked"].fillna("S")

    titanic.loc[titanic["Embarked"]=="S","Embarked"]=0
    titanic.loc[titanic["Embarked"]=="C","Embarked"]=1
    titanic.loc[titanic["Embarked"]=="Q","Embarked"]=2

    titanic["Fare"]= titanic["Fare"].fillna(titanic["Fare"].median())return titanic

train_data = harmonize_data(train)

predictors =["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked"]
results =[]
sample_leaf_options =list(range(1,500,3))
n_estimators_options =list(range(1,1000,5))
groud_truth = train_data['Survived'][601:]for leaf_size in sample_leaf_options:for n_estimators_size in n_estimators_options:
        alg = RandomForestClassifier(min_samples_leaf=leaf_size, n_estimators=n_estimators_size, random_state=50)
        alg.fit(train_data[predictors][:600], train_data['Survived'][:600])
        predict = alg.predict(train_data[predictors][601:])# 用一个三元组，分别记录当前的 min_samples_leaf，n_estimators， 和在测试数据集上的精度
        results.append((leaf_size, n_estimators_size,(groud_truth == predict).mean()))# 真实结果和预测结果进行比较，计算准确率print((groud_truth == predict).mean())# 打印精度最大的那一个三元组print(predict)print(max(results, key=lambda x: x[2]))

输出为：测试集上达到84%的预测准确率，但是运行时间比较久

0.73103448275862070.81034482758620690.80.81034482758620690.80.80.79310344827586210.79310344827586210.79310344827586210.80.79310344827586210.79655172413793110.8034482758620690.8034482758620690.8034482758620690.8034482758620690.81034482758620690.80689655172413790.8034482758620690.8.........

总结

随机森林算法模型的评估：

一般使用训练集 (training set) 建立模型，使用测试集 (test set) 来评估模型。对于分类算法评估指标有分类准确度、召回率、虚警率和精确度等。而这些指标都是基于混淆矩阵 (confusion matrix) 进行计算的。

混淆矩阵用来评价监督式学习模型的精确性，矩阵的每一列代表一个类的实例预测，而每一行表示一个实际的类的实例。以二分类问题为例，如下表所示：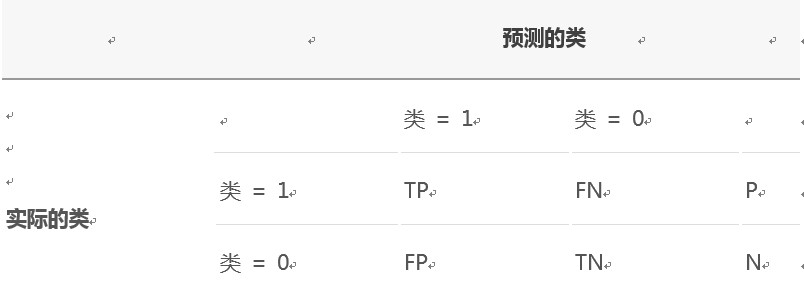

其中
P (Positive Sample)：正例的样本数量。
N (Negative Sample)：负例的样本数量。
TP (True Positive)：正确预测到的正例的数量。
FP (False Positive)：把负例预测成正例的数量。
FN (False Negative)：把正例预测成负例的数量。
TN (True Negative)：正确预测到的负例的数量。

根据混淆矩阵可以得到评价分类模型的指标有以下几种。

分类准确度，就是正负样本分别被正确分类的概率，计算公式为：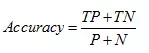

召回率，就是正样本被识别出的概率，计算公式为：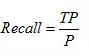

虚警率，就是负样本被错误分为正样本的概率，计算公式为：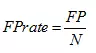

精确度，就是分类结果为正样本的情况真实性程度，计算公式为：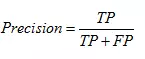

评估方法有保留法、随机二次抽样、交叉验证和自助法等。

• 保留法 (holdout) 是评估分类模型性能的最基本的一种方法。将被标记的原始数据集分成训练集和检验集两份，训练集用于训练分类模型，检验集用于评估分类模型性能。但此方法不适用样本较小的情况，模型可能高度依赖训练集和检验集的构成。
• 随机二次抽样 (random subsampling) 是指多次重复使用保留方法来改进分类器评估方法。同样此方法也不适用训练集数量不足的情况，而且也可能造成有些数据未被用于训练集。
• 交叉验证 (cross-validation) 是指把数据分成数量相同的 k 份，每次使用数据进行分类时，选择其中一份作为检验集，剩下的 k-1 份为训练集，重复 k 次，正好使得每一份数据都被用于一次检验集 k-1 次训练集。该方法的优点是尽可能多的数据作为训练集数据，每一次训练集数据和检验集数据都是相互独立的，并且完全覆盖了整个数据集。也存在一个缺点，就是分类模型运行了K 次，计算开销较大。
• 自助法 (bootstrap) 是指在其方法中，训练集数据采用的是有放回的抽样，即已经选取为训练集的数据又被放回原来的数据集中，使得该数据有机会能被再一次抽取。用于样本数不多的情况下，效果很好。