【数据结构初阶】简析堆排序

一、引言

通过之前的学习，让我们对堆的概念有了大致的了解，

想了解 堆 基础知识的同学看这里： 二叉树（堆）基础知识

今天就让我们一起来学习一下堆排序的内容：

堆排序相较于我们以前学过的C语言冒泡排序，它的效率达到了基于比较的排序算法效率的峰值（时间复杂度为O(nlogn)），具有显著优势

堆排序即利用堆的思想来进行排序

二、建堆方法的比较

我们都知道堆排序是以堆的逻辑结构为基础的，建堆的方法通常有两种

• 向上调整建堆
• 向下调整建堆

向上调整建堆，每插入一个数，向上调整一次（也就是说，要从根节点开始，遍历所有节点）

向下调整建堆，从倒数第一个非叶子节点（最后一个节点的父亲）开始调整，逐个向下调整，只需要遍历除叶子节点以外的节点就可以了

因此，我们通常会使用向下调整建堆，因为向下调整建堆的时间复杂度更小

为了更好的说明二者的差别，我们来看一组对比图：

向下调整建堆时间复杂度：

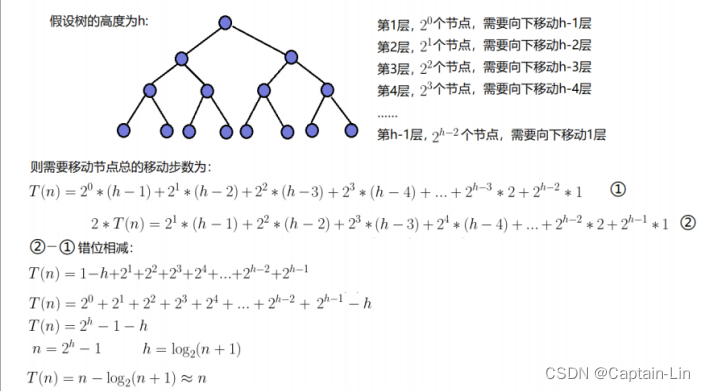
向上调整建堆时间复杂度（以最后一层为例）：

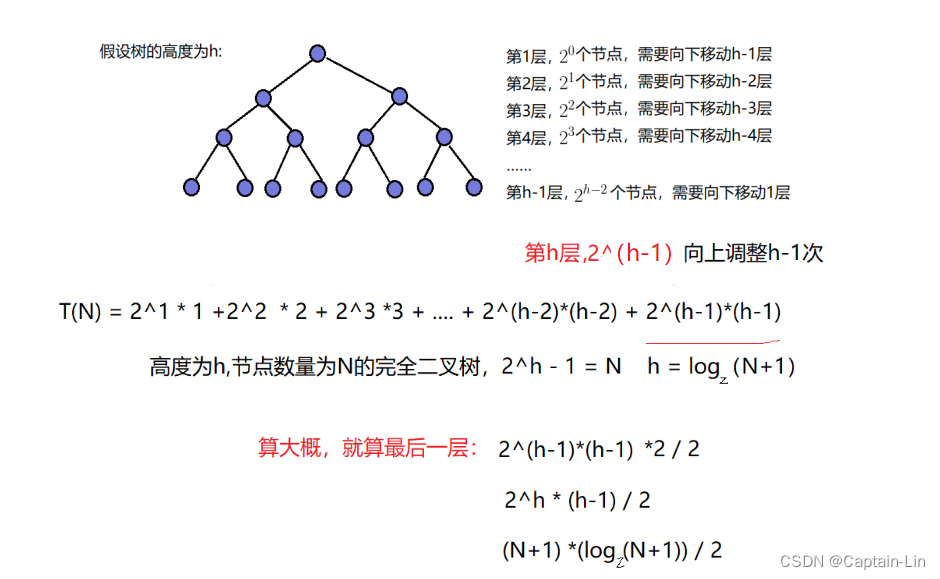
即使是最后一层调整，它的时间复杂度也已经达到（n+1）(log(n+1))/2，最终全部层数加起来，时间复杂度的级别应为 *nlogn* 级别

对比向下调整的n级别，易得向下调整建堆更具有优势。

【注意】建好堆之后并不相当于有序

三、堆排序

1.建堆

• 升序：建大堆
• 降序：建小堆

为什么要这样建堆呢？一是方便选数，二是避免父子大小关系混乱（第一个最小数排好后，如果把剩下的数看作堆，那么父子关系全乱了）

同时我们也可以从时间复杂度上来思考：

升序：建大堆（N*logN —— N个数，排logN次）

       建小堆（N*N —— N个数，排N次）

2.利用堆删除思想进行排序

我们这里以 升序->建大堆 为例

void AdjustDown(HPDataType* a, int n, int parent)
{
    int minChild = parent * 2 + 1;
    while (minChild < n)
    {
        // 找出大的那个孩子
        if (minChild + 1 < n && a[minChild + 1] > a[minChild])
        {
            minChild++;
        }

        if (a[minChild] > a[parent])
        {
            Swap(&a[minChild], &a[parent]);
            parent = minChild;
            minChild = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

void HeapSort(int* a, int n)
{
    // 大思路：建堆，依次选数，从后往前排
    // 升序 -- 大堆
    // 降序 -- 小堆
    // 建堆 -- 向下调整建堆 - O(N)
    for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    {
        AdjustDown(a, n, i);
    }

    // 选数 
    int i = 1;
    while (i < n)
    {
        Swap(&a[0], &a[n - i]);//交换第一个和最后一个
        AdjustDown(a, n - i, 0);//数组地址+尾部处+开始处
        ++i;
    }
}

int main()
{
    int a[] = { 15, 1, 19, 25, 8, 34, 65, 4, 27, 7 };
    HeapSort(a, sizeof(a) / sizeof(int));

    for (size_t i = 0; i < sizeof(a) / sizeof(int); ++i)
    {
        printf("%d ", a[i]);
    }
    printf("\n");

    return 0;
}

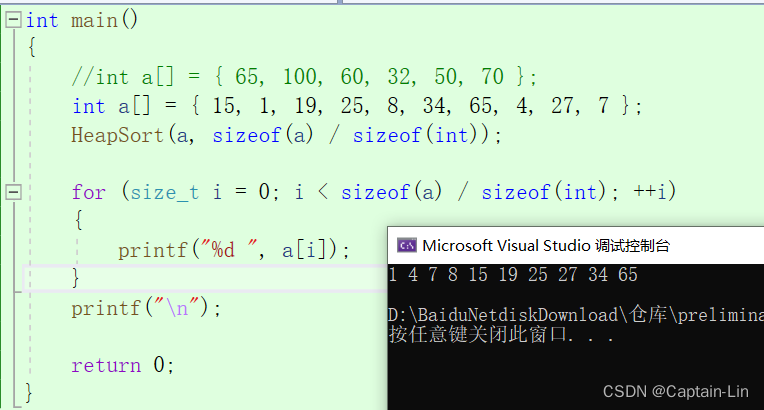
** 降序->建小堆 **的方法也类似，这里就不在多赘述了，有兴趣的小伙伴可以自己尝试一下

** 【理解】升序：大的在叶子节点；降序：小的在叶子节点**

四、总结

堆排序方法：

1.向下调整建堆（升序->大堆，降序->小堆）

2.头尾数交换，向下调整