数据结构java版之堆

明天就除夕啦，在这里提前祝大家，新的一年万事胜意

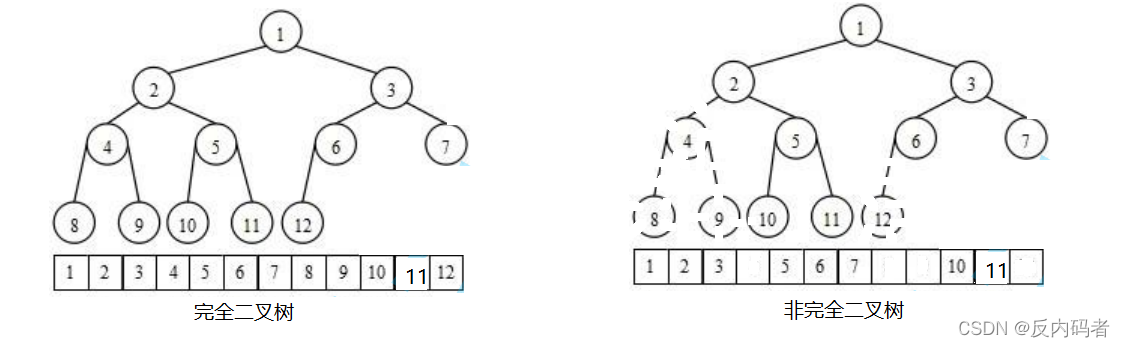
使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。 一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。 即用堆来表示就是用完全二叉树来表示。

由图可见，对于非完全二叉树而言，浪费了很多空间。所以堆的表示用的是完全二叉树的表示方法

2.下标关系

①已知双亲(parent)的下：

左孩子(left)下标 = 2 * parent + 1;

右孩子(right)下标 = 2 * parent + 2;

②已知孩子（不区分左右）(child)下标：

双亲(parent)下标 = (child - 1) / 2

二、堆

①堆逻辑上是一棵完全二叉树

②堆物理上是保存在数组中

③满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆

（注意：在整棵树中中的子树均要满足这个条件）

④反之，则是小堆，或者小根堆，或者最小堆（注意：在整棵树中中的子树均要满足这个条件）

⑤ 堆的基本作用是，快速找集合中的最值

体现在下面的操作中

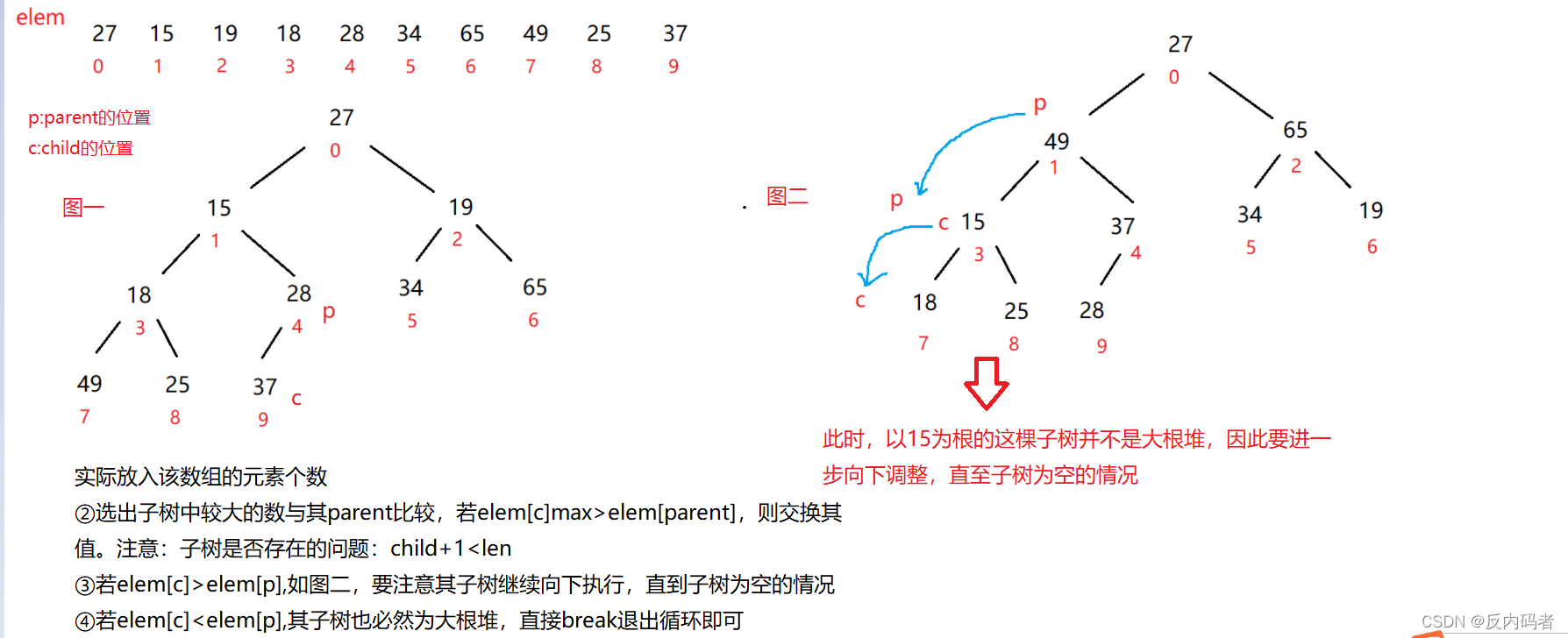
要点：左右子树必须已经是一个堆，才能调整。以大堆举例，最后调整成一棵大根堆的形式

①调整是从最后一棵子树出发的

②每棵子树均是向下调整的

？？？问题？？？

①如何找到最后一棵树的子树

前面有提到：(len-1)可以找到最后一棵子树的下标；且

parent=((len-1)-1)/2

②如何遍历

parent--就可以遍历完每棵子树了

③究竟如何实现

用一个向下调整的函数来 实现

④每棵树调整结束的位置如何判定？

每棵树调整的结束位置，实际上都是一样的len

具体实现思路：

代码如下：

public class TestHeap {
    public int []elem;
    //用来记录实际放入数组的元素个数
    public int usedSize;
    public TestHeap(){
        this.elem=new int[10];
    }//向下调整
    //parent:每棵树的根结点
    //len:每棵树调整的结束位置
    public void shiftDown(int parent,int len) {
        int child = parent * 2 + 1;
        //该子树至少有一个左孩子
        while (child < len) {
            if (child + 1 < len && elem[child] < elem[child + 1]) {
                //用来保证取的值是当前左右孩子中较大值的下标
                child++;
            }//情况①，elem[c]>elem[p]且p,c需要继续向下检测
            if (elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                parent = child;
                child = 2 * parent + 1;
            }//情况②，elem[c]<elem[p]，其子树也必然为大根堆，所以可以直接退出循环
            else {
                break;
            }
        }
    }
            //创建大根堆
            public void createHeap( int[] array){
                for (int i = 0; i < array.length; i++) {
                    elem[i] = array[i];
                    this.usedSize++;
                }
                for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {
                    //向下调整
                    shiftDown(parent, usedSize);
                }
            }
    }

时间复杂度分析：

粗略估算，可以认为是在循环中执行向下调整，为 O(n * log(n)) （了解）实际上是 O(n) 堆排序中建堆过程时间复杂度O(n)怎么来的？

大家可以参考一下这篇文章，这里就不详细解释了

堆排序中建堆过程时间复杂度O(n)怎么来的？ - 知乎 (zhihu.com)https://www.zhihu.com/question/20729324

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次 高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。

这种数据结构就是优先级队列(Priority Queue)

优先级队列的实现方式有很多，但最常见的是使用堆来构建。

解题思路：(实质上为一个向上调整)

①将要入队元素放于该队列的队尾，要是原队列已满的话进行扩容

②找到该节点及其父亲结点，比较两者的值，若elem[child] > elem[parent]即进行交换，反之退出循环

③注意：因为原树已经调节好了，所以此时入队的时候只需要和每棵子树的父亲结点进行比较，循环结束的条件为child<0;

代码：

//向上调整
    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if(elem[child] > elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }

    public void offer(int val) {
        if(isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize++] = val;
        //此处传入的是下标值，因此注意这里传入的是usedSize-1
        shiftUp(usedSize-1);
    }

    public boolean isFull() {
        return usedSize == elem.length;
    }

注意：每次出队列必须保证出最大的或者最小的

解题思路：

①交换0下标和最后一个元素

②调整0下标这棵树即可（向下调整）

代码如下：

 public int poll(){
        if(isEmpty()){
            throw new RuntimeException("此优先队列为空！");
        }int tmp=elem[0];
        elem[0]=elem[usedSize--];
        elem[usedSize--]=tmp;
        usedSize--;
        shiftDown(0,usedSize);
        return tmp;
    }
    public boolean isEmpty(){
        return usedSize==0;
    }

 public int peek(){
        if(isEmpty()){
            throw new RuntimeException("此优先队列为空！");
        }
        return elem[0];
    }

将会在下一节博客中讲述