时空图卷积网络:用于交通预测的深度学习框架
及时准确的交通预测对城市交通控制和引导至关重要。由于交通流的高度非线性和复杂性,传统的方法不能满足中长期预测任务的要求,往往忽略了空间和时间的相关性。本文提出了一种新的深度学习框架——时空图卷积网络(spatial - temporal Graph Convolutional Networks, STGCN)来解决交通域的时间序列预测问题。我们不使用正则卷积和递归单元,而是在图上表达问题,并建立具有完整卷积结构的模型,这使训练速度更快,参数更少。实验表明,我们的模型STGCN通过对多尺度交通网络建模,有效地捕获了综合的时空相关性,并始终优于各种真实世界交通数据集的最先进的基线。
1 Introduction
交通在每个人的日常生活中起着至关重要的作用。根据2015年的一项调查,美国司机平均每天在方向盘后面花费48分钟在这种情况下,准确实时的交通状况预测对道路使用者、私营部门和政府来说至关重要。广泛使用的交通服务,如流量控制、路线规划和导航,也在很大程度上依赖于高质量的交通状况评估。总体而言,多尺度交通预测是城市交通控制与引导的前提和基础,也是智能交通系统的主要功能之一。在交通研究中,通常选择交通流的基本变量,即速度、流量和密度作为监测当前交通状况和的指标预测未来。根据预测的长度,交通预测一般分为两个尺度:短期(5 ~ 30分钟)、中期和长期(30分钟以上)。大多数流行的统计方法(例如,线性回归)能够在短区间预测中表现良好。然而,由于交通流的不确定性和复杂性,这些方法对于相对长期的预测效果较差。
以往关于中长期交通预测的研究大致可以分为两大类:动态建模和数据驱动方法。动力学建模使用数学工具(如微分方程)和物理知识,通过计算仿真来制定交通问题[Vlahogianni, 2015]。为了达到稳态,仿真过程不仅需要复杂的系统编程,而且需要消耗大量的计算能力。模型中不切实际的假设和简化也会降低预测精度。因此,随着交通数据采集和存储技术的快速发展,大量的研究人员开始将注意力转向数据驱动的方法。
经典的统计模型和机器学习模型是数据驱动方法的两个主要代表。在时间序列分析中,自回归综合移动平均(ARIMA)及其变体是基于经典统计的最统一的方法之一[Ahmed and Cook, 1979;Williams和Hoel, 2003]。然而,这类模型受时间序列平稳假设的限制,未能考虑到时空相关性。因此,这些方法限制了高度非线性交通流的可表征性。近年来,经典的统计模型受到了交通预测任务中的机器学习方法的挑战。这些模型可以实现更高的预测精度和更复杂的数据建模,如k近邻算法(KNN)、支持向量机(SVM)和神经网络(NN)。
目前,深度学习方法已经被广泛成功地应用于各种交通任务中。相关工作取得了显著进展,如深度信念网络(DBN) [Jia等人,2016;黄等人,2014],stacked autoencoder (SAE) [Lv等人,2015;Chen等,2016]。然而,对于这些密集的arXiv:1709.04875v4 [cs]来说,这是困难的。LG] 2018年7月12日联合网络从输入中提取时空特征。此外,在狭窄的约束条件下,甚至在完全缺乏空间属性的情况下,这些网络的代表能力将受到严重的阻碍。
为了充分利用空间特征,一些研究人员使用卷积神经网络(CNN)捕捉交通网络之间的相邻关系,并在时间轴上使用回归神经网络(RNN)。Wu和Tan[2016]结合长-短期记忆(LSTM)网络[Hochreiter和Schmidhuber, 1997]和一维CNN,提出了一种用于短期交通预测的特征级融合架构CLTFP。尽管它采用了一个直截了当的策略,CLTFP仍然第一次尝试对齐空间和时间的规律。随后,Shi等人[2015]提出了卷积LSTM,它是一种嵌入卷积层的扩展全连接LSTM (FC-LSTM)。然而,常规的卷积运算限制模型只能处理网格结构(如图像、视频),而不能处理一般领域。同时,用于序列学习的递归网络需要迭代训练,引入了误差逐步积累。此外,众所周知,基于rnn的网络(包括LSTM)训练困难且计算量大
为了克服这些问题,我们引入了几种策略来有效地建模交通流的时间动力学和空间依赖性。为了充分利用空间信息,我们用一般图形来建模交通网络,而不是单独对待它(如网格或分段)。为了解决递归网络的固有缺陷,我们采用了时间轴上的全卷积结构。首先,我们提出了一种新的深度学习架构——时空图卷积网络,用于交通预测任务。该架构包括几个时空卷积块,它们是图卷积层[Defferrard等人,2016]和卷积序列学习层的组合,以建模空间和时间依赖性。据我们所知,在交通研究中应用纯卷积结构同时从图结构时间序列中提取时空特征尚属首次。我们在两个真实世界的交通数据集上评估我们提出的模型。实验表明,该框架在具有多个预估长度和网络规模的预测任务中性能优于现有的基线。
2 Preliminary
2.1基于道路图的交通预测
交通预测是一个典型的时间序列预测问题,即在给定之前的M个交通观测值的情况下,预测下一个H时间步中最可能的交通测量值(例如速度或交通流量):
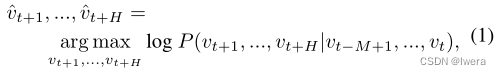
其中vt∈Rn是n个路段在时间步长t时的观测向量,每个元素记录单个路段的历史观测值。
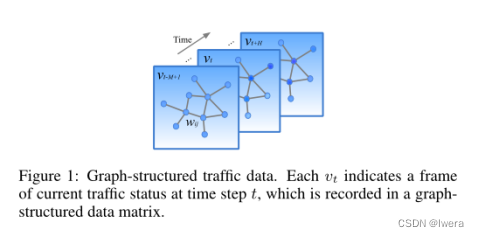
在这项工作中,我们在一个图上定义交通网络,并重点关注结构化交通时间序列。观察vt在图中不是独立的,而是通过成对连接连接的。因此,数据点vt可以看作是一个图信号,定义在一个权值为wij的无向图(或有向图)G上,如图1所示。在第t个时间步时,在图Gt = (Vt, E, W)中,Vt是顶点的有限集,对应于交通网络中n个监测站的观测值;E是边的集合,表示站与站之间的连通性;W∈Rn×n表示Gt的加权邻接矩阵。
2.2图上的卷积
规则网格的标准卷积显然不适用于一般图。目前有两种基本的方法来探索如何将cnn推广到结构化数据形式。一种是扩展卷积的空间定义[Niepert等人,2016],另一种是利用图傅里叶变换在光谱域进行操作[Bruna等人,2013]。前一种方法将顶点重新排列成特定的网格形式,这些网格形式可以通过普通的卷积运算进行处理。后者引入光谱框架将卷积应用于光谱域,通常称为谱图卷积。一些后续研究通过将计算复杂度从O(n2)降低到线性,使图卷积更有前途[Defferrard等人,2016;Kipf和Welling, 2016]。
我们引入了基于谱图卷积概念的图卷积算子* G的概念,它是信号x∈Rn与核Θ的乘积,
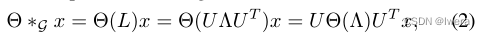
其中,图傅里叶基U∈Rn×n为归一化图Laplacian L = In−D−1 2 W D−1 2 = UΛU T∈Rn×n的特征向量矩阵(In为单位矩阵,D∈Rn×n为Dii = ΣjWij的对角度矩阵);Λ∈Rn×n是L的特征值的对角矩阵,filter Θ(Λ)也是一个对角矩阵。根据这个定义,一个图信号x被内核Θ滤波,Θ与图傅里叶变换U T x相乘[Shuman等人,2013]。
3提出的模型
3.1网络体系结构
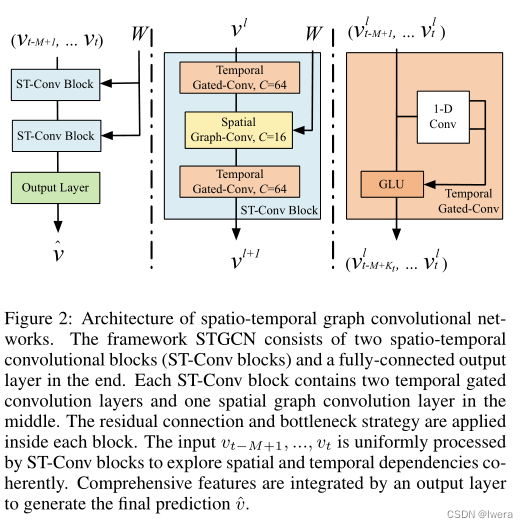
在本节中,我们详细阐述了提出的时空图卷积网络(STGCN)架构。如图2所示,STGCN由多个时空卷积块组成,每个卷积块形成一个“三明治”结构,中间有两个门控顺序卷积层和一个空间图卷积层。各模块的详细信息如下所示。
3.2用于提取空间特征的图cnn
交通网络通常以图的形式组织。用数学的方法来表示路网是自然而合理的。然而,以往的研究忽略了交通网络的空间属性:由于将交通网络划分为多个区段或网格,忽视了交通网络的连通性和全局性。即使是网格上的二维卷积,由于数据建模的妥协,它也只能粗略地捕获空间局部性。因此,在我们的模型中,直接对图结构数据使用图卷积来提取空间域中高度有意义的模式和特征。虽然通过Eq.(2)计算图卷积中的核Θ可能会因为O(n2)乘图傅里叶基而代价高昂,但我们采用了两种近似策略来克服这个问题。
切比雪夫多项式近似** **为了定位滤波器并减少参数的数量,核Θ可以被限制为Λ的一个多项式Θ(Λ) = PK−1 k=0 θkΛk,其中θ∈RK是多项式系数的一个向量。K是图卷积的核大小,它决定了从中心节点卷积的最大半径。传统上,Chebyshev多项式Tk(x)用于近似核,作为顺序K−1的截断扩展为Θ(Λ)≈PK−1 K =0 θkTk(˜Λ)和重标的˜Λ = 2Λ/λmax−In (λmax表示L的最大特征值)[Hammond et al., 2011]。图卷积可以被重写为,
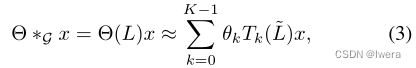
其中Tk(˜L)∈Rn×n是序k的Chebyshev多项式,在缩放的Laplacian˜L = 2L/λmax−In。通过多项式逼近递归计算K局域卷积,Eq.(2)的代价可以降为O(K|E|),如Eq.(3)所示[Defferrard et al., 2016]。
1阶近似** **用图拉普拉斯一阶近似叠加多个局部图卷积层可以定义分层线性公式[Kipf和Welling, 2016]。因此,可以构建一个更深入的体系结构,在不局限于多项式所给出的显式参数化的情况下对空间信息进行深度恢复。由于神经网络的尺度化和归一化,我们可以进一步假设λmax≈2。因此,式(3)可简化为:
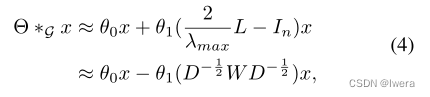
其中,θ0, θ1是核的两个共享参数。为了约束参数和稳定数值性能,θ0和θ1用单一参数θ代替,使θ = θ0 =−θ1;W和D分别被˜W = W + In和˜Dii = Σj˜Wij。那么,图卷积可以交替表示为:
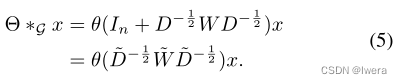
在垂直方向上应用一阶近似的图卷积堆栈,可以获得与水平方向上klocalized卷积类似的效果,所有这些都利用了中心节点的(K−1)阶邻域的信息。在这种情况下,K是一个模型中连续过滤操作或卷积层的数量。此外,分层线性结构对大规模图具有参数经济和高效的特点,因为近似的阶数限制在1。
图卷积的推广** *定义在x∈Rn上的图卷积算子 G可以推广到多维张量。对于Ci信道X∈Rn×Ci的信号,其图卷积可推广为:
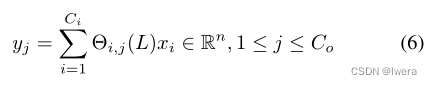
的切比雪夫系数Θi,j∈RK (Ci, Co分别为特征图输入和输出的大小)的Ci × Co向量。二维变量的图卷积记为“Θ * G X”,其中Θ∈RK×Ci×Co。其中,交通预测的输入由道路图的M帧组成,如图1所示。每一帧vt可以被看作是一个矩阵的列我是Ci-dimensional vt的价值在第i个节点图Gt,当X∈Rn×Ci(在这种情况下,Ci = 1)。对于每个时间步t M等于图卷积操作相同的内核Θ对Xt∈Rn×Ci并行。因此,图卷积可以进一步推广到3-D变量中,记为“Θ * G X”,X∈RM×n×Ci。
3.3门控cnn提取时间特征
尽管基于rnn的模型在时间序列分析中得到广泛应用,但用于流量预测的递归网络仍然存在迭代耗时、门控机制复杂、对动态变化响应缓慢等问题。相反,cnn具有训练速度快、结构简单、不依赖前几步的优势。受[Gehring et al., 2017]启发,我们采用时间轴上的全卷积结构来捕捉交通流的时间动态行为。这种特殊的设计允许通过形成分层表示的多层卷积结构并行和可控的训练程序。如图2(右)所示,时间卷积层包含一个具有宽度- kt核的一维因果卷积,后面是一个非线性的门控线性单元(GLU)。对于图G中的每个节点,时间卷积在不填充的情况下探索输入元素的Kt邻居,使得序列的长度每次缩短Kt-1。因此,每个节点的时间卷积输入可以看作是一个长度- m序列,Ci通道为Y∈RM×Ci。卷积核Γ∈RKt×Ci×2Co用于将输入Y映射到单个输出元素[P Q]∈R(M−Kt+1)×(2Co) (P, Q被一分为二,通道大小相同)。因此,时间门控卷积可以定义为:
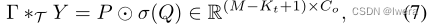
式中,P、Q分别为GLU中的门的输入;? 表示元素级的阿达玛乘积。sigmoid gate σ(Q)控制哪些输入P的电流状态与发现时间序列中的成分结构和动态方差有关。非线性门还有助于通过叠加的时间层利用全输入场。此外,在堆叠的时间卷积层之间实现剩余连接。同样,通过对G中的每个节点Yi∈RM×Ci(例如传感器站)使用相同的卷积核Γ,时间卷积也可以推广到3-D变量,记为“Γ * T Y”和Y∈RM×n×Ci。
3.4时空卷积块
为了融合时空两方面的特征,构造了时空卷积块(ST-Conv块)来联合处理图结构时间序列。块本身可以根据特定情况的规模和复杂性进行堆叠或扩展。
如图2(中间)所示,中间的空间层是连接两个时间层,可以通过时间卷积从图卷积实现快速的空间状态传播。“三明治”结构也有助于网络充分运用瓶颈策略,通过图卷积层对通道C进行降尺度和升尺度,实现尺度压缩和特征压缩。此外,在ST-Conv的每个块内都进行了层归一化,以防止过拟合。
ST-Conv块的输入和输出都是三维张量。对于块l的输入vl∈RM×n×Cl,输出vl+1∈R(M−2(Kt−1))×n×Cl+1的计算公式为:
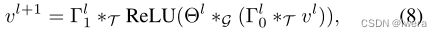
式中Γl0、Γl1分别为第l块内的上、下时间核;Θl是图卷积的谱核;ReLU(·)为修正后的线性单元函数。在叠加两个ST-Conv块后,我们在最后附加一个全连通的时间卷积层作为输出层(见图2左侧)。时间卷积层将最后一个ST-Conv块的输出映射到一个单步预测。然后,我们可以从模型中得到最终输出Z∈Rn×c,并通过跨c通道的线性变换计算n个节点的速度预测,即ˆv = Zw + b,其中w∈Rc为权向量,b为偏置。我们使用L2损失来衡量我们的模型的性能。则STGCN流量预测的损失函数为:
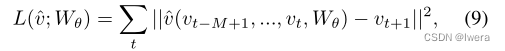
其中Wθ均为模型可训练参数;Vt +1为地面真值,ˆv(·)为模型预测。
下面我们将我们的模型STGCN的主要特点总结如下:
1、STGCN是处理结构化时间序列的通用框架。它不仅能够解决交通网络建模和预测问题,而且还可以应用于更一般的时空序列学习任务。
2、时空块结合了图卷积和门控时间卷积,可以提取最有用的空间特征和最基本的时间特征。
3、该模型完全由卷积结构组成,以更少的参数和更快的训练速度实现了输入的并行化。更重要的是,这种经济架构允许模型更有效地处理大规模网络。
4实验
4.1数据集描述
我们利用北京市交通委员会和美国加州交通部分别收集的真实交通数据集BJER4和PeMSD7验证了我们的模型。每个数据集包含交通观测的关键属性和带有相应时间戳的地理信息,如下所示。
BJER4在北京市东环4号线主要区域采用双环检测方法采集。我们选择了12条路进行实验。每5分钟聚合一次。使用的时间段为2014年7月1日至8月31日,周末除外。我们选取历史速度记录的第一个月作为训练集,其余分别作为验证集和测试集。
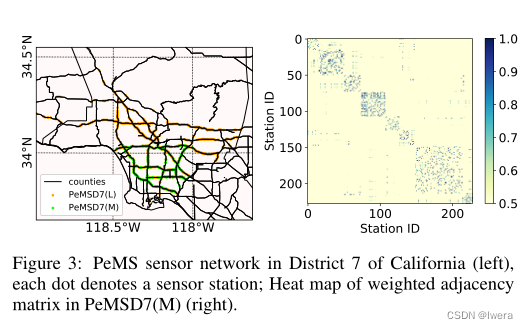
PeMSD7是由部署在加州高速公路系统主要都市地区的超过39000个传感器站实时从加州公路性能测量系统(PeMS)收集的[Chen等人,2001]。数据集还从30秒的数据样本聚合为5分钟间隔。我们在加州第7区中随机选择一个中等规模和一个大型规模,分别为228和1026数据来源分别为PeMSD7(M)和PeMSD7(L),如图3左侧所示。PeMSD7数据集的时间范围为2012年5月和6月的工作日。我们基于上述相同的原则对训练集和测试集进行划分。
4.2数据预处理
两个数据集的标准时间间隔设置为5分钟。因此,道路图的每个节点每天包含288个数据点。在数据清理后,利用线性插值方法对缺失值进行补全。此外,对输入的数据采用Z-Score方法进行归一化处理。
在BJER4中,通过传感器站布置图构建北京东四环路网系统的路网拓扑。通过核对每条道路的从属关系、方向和起落点,环线系统可以数字化为一个有向图。
在PeMSD7中,基于交通网络中站点之间的距离计算道路图的邻接矩阵。加权邻接矩阵W可以表示为:
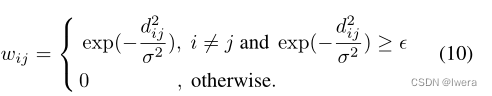
其中wij为边的权值,由dij(站I到站j的距离)决定。为控制矩阵W的分布和稀疏度的阈值,分别赋值为10和0.5。W的可视化如图3的右侧所示
4.3实验设置
所有实验都在Linux集群上编译和测试(CPU: Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10GHz, GPU: NVIDIA GeForce GTX 1080)。为了消除非典型交通,我们的实验只采用工作日交通数据[Li et al., 2015]。我们执行网格搜索策略来定位验证中的最佳参数。所有测试都使用60分钟作为历史时间窗口,也就是12个观测数据点(M = 12)用于预测未来15、30和45分钟(H = 3、6、9)的交通状况。
评估标准和基线** **测量和评估不同方法的性能,平均绝对误差(MAE),平均绝对百分比误差(MAPE)和采用均方根误差(RMSE)。我们将我们的框架STGCN与以下基线进行比较:1).历史平均(HA);2).线性支持维克多回归(LSVR);3).自回归综合移动平均(ARIMA);4)前馈神经网络(FNN);5).全连接LSTM (FC-LSTM) [Sutskever et al., 2014];6). Graph Convolutional GRU (GCGRU) [Li等人,2018]。
*STGCN*****模型 ****对于BJER4和PeMSD7(M/L), ST-Conv块的三层通道分别为64、16、64。模型STGCN(Cheb)通过Chebyshev多项式近似取图卷积核大小K和时间卷积核大小Kt为3,而模型STGCN(1)通过一阶近似取K为1。我们通过使用RMSprop最小化均方误差来训练我们的模型,50个时期的批大小为50。初始学习速率为10−3,每5个epoch后衰减速率为0.7。
4.4实验结果
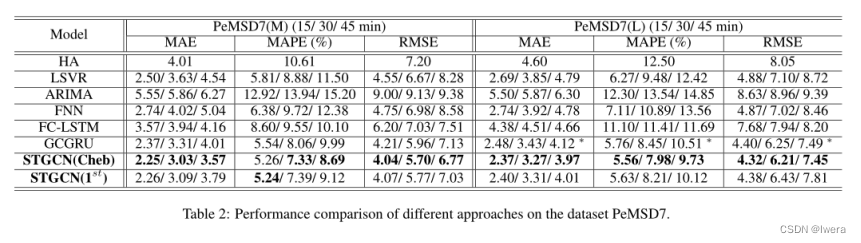
表1和2展示了STGCN和基线在数据集BJER4和PeMSD7(M/L)上的结果。我们提出的模型在所有三个评价指标上都具有统计学显著性(双尾t检验,α = 0.01, P < 0.01),从而实现了最佳的性能。我们可以很容易地观察到,传统的统计和机器学习方法可能在短期预测中表现良好,但它们的长期预测并不准确,因为错误积累、记忆问题和空间信息的缺乏。ARIMA模型由于不能处理复杂的时空数据而表现最差。深度学习方法通常比传统的机器学习模型获得更好的预测结果。
空间拓扑的好处
以前的方法没有结合空间拓扑,也没有以粗粒度的方式对时间序列建模。不同的是,通过对传感器空间拓扑的建模,我们的模型STGCN在短期和中期预测方面取得了显著的改进。STGCN在数据集PeMSD7上的优势比BJER4更明显,因为PeMS的传感器网络更复杂、更结构化(如图3所示),我们的模型可以有效地利用空间结构进行更准确的预测。
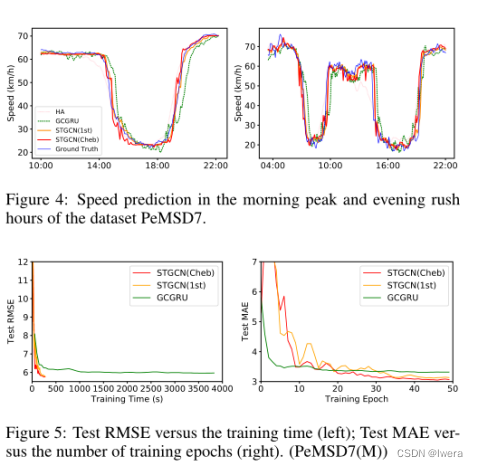
为了比较基于图卷积的三种方法:GCGRU, STGCN(Cheb)和STGCN(1st),我们展示了它们的早高峰和晚高峰时段的预测,如图4所示。不难看出,我们的建议STGCN比其他方法更准确地捕捉到高峰时间的趋势;它能比其他时间更早地检测到高峰时段的结束。基于高效的图卷积和叠加的时间卷积结构,我们的模型能够快速响应交通网络之间的动态变化,而不像大多数循环网络那样过度依赖历史平均。
训练效率与概化
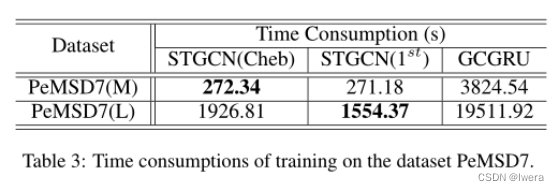
为了看到我们的方案中沿时间轴卷积的好处,我们在表3中总结了STGCN和GCGRU训练时间的比较。在公平性方面,在PeMSD7(M)实验中,GCGRU分为三层,分别为64,64,128个单元,STGCN采用4.3节的默认设置。我们的模型STGCN只消耗272秒,而rnn型的模型GCGRU在PeMSD7(M)上花费3824秒。这14倍的训练速度的加速主要得益于使用时间卷积而不是循环结构,可以实现完全并行训练,而不是完全依赖链结构作为RNN做的。对于PeMSD7(L), GCGRU需要使用批大小的一半,因为它的GPU消耗超过了单个卡的内存容量(结果在表2中标记为“*”);而STGCN只需要将ST-Conv块中间的信道加倍即可。尽管在这种情况下,我们的模型所消耗的训练时间还不到模型GCGRU的十分之一。同时,由于不局限于多项式的参数化,一阶近似的优点也显现出来。与STGCN(Cheb)相比,模型STGCN(1)在更大的数据集上加速约20%,性能令人满意。
为了进一步研究比较的深度学习模型的性能,我们绘制了PeMSD7(M)测试集在训练过程中的RMSE和MAE,见图5。这些数据还表明,我们的模型可以实现更快的训练过程和更容易的收敛。由于ST-Conv模块的特殊设计,我们的模型在平衡时间消耗和参数设置方面具有优越的性能。其中STGCN的参数数量(4.54 × 105)仅占GCGRU的2 / 3左右,比FC-LSTM节省了95%以上的参数。
5相关工作
最近有几项深度学习研究也受到时空任务中的图卷积的启发。Seo等人[2016]引入了图卷积递归网络(GCRN),从数据的结构化序列中联合识别空间结构和动态变化。本研究的关键挑战是确定在特定设置下递归网络和图卷积的最优组合。基于上述原理,Li等人[2018]成功地将门控循环单元(GRU)与图卷积结合用于长期交通预测。与这些作品相反,我们完全从卷积结构建立我们的模型;ST-Conv块是专门设计的,用于统一处理内部带有剩余连接和瓶颈策略的结构化数据;在我们的模型中使用了更有效的图卷积核。
6结论与未来工作
本文提出了一种新的用于交通预测的深度学习框架STGCN,通过时空卷积块集成图卷积和门控时间卷积。实验表明,我们的模型在两个真实数据集上的表现优于其他最先进的方法,表明它在从输入数据探索时空结构方面具有巨大的潜力。它还实现了更快的训练、更容易的收敛和更少的参数,具有灵活性和可伸缩性。这些特性对于学术开发和大规模行业部署来说是非常有前景和实用的。未来,我们将进一步优化网络结构和参数设置。此外,我们提出的框架可以应用于更一般的时空结构序列预测场景,如社会网络的进化,以及推荐系统中的偏好预测等。
版权归原作者 lwera 所有, 如有侵权,请联系我们删除。