🧡🧡实验内容🧡🧡
TSP问题是组合数学中一个古老而又困难的问题,也是一个典型的组合优化问题,现已归入NP完备问题类。NP问题用穷举法不能在有效时间内求解,所以只能使用启发式搜索。遗传算法是求解此类问题比较实用、有效的方法之一。下面给出30个城市的位置信息:
应用遗传算法和蚁群优化算法求解30/10个节点的TSP(旅行商问题)问题,求问题的最优解。
🧡🧡遗传算法求解🧡🧡
主要参数定义
染色体的定义:
每一条染色体定义为一条路线,其上的基因代表城市编号,例如:染色体:[5,1,2,3,4],,代表路径为5->1->2->3->4->5。
适应度的定义:
路径之间的距离和,是使得这个值最小,而本实验为方便轮盘赌根据适应度大小选择染色体,取路径距离和的负值,即在求解过程中保留适应度大的染色体。 例如:染色体:[5,1,2,3,4],,代表 min( len(5->1) + len(1->2) + len(2->3) + len(3->4) + len(4->5) )。
选择操作:
采用轮盘赌的选择方法,适应度大的更有机会被选择到。
交叉操作:
为确保每个城市只走一次,因此染色体交叉前后,其上面的基因都应该满足含有城市编号1~N(N为城市个数),且各个基因不重复,因此采用如下交叉方式
变异操作:
对染色体进行两点变异,也可逆转变异(根据变异前后最优适应度对比,决定是否采用变异)
交叉率和变异率:
每一根染色体都有可能进行交叉和突变,取决于交叉率和突变率。
种群规模(染色体数量):
大的种群可以保证每一代里拥有的染色体更多,交叉和突变得到的新染色体更多,有助于跳出局部最优解,尽早获得全局最优解。
代码
clear all;
close all;
clc;%% 初始化参数% 生成城市坐标
C=[87,7;91,38;83,46;71,44;64,60;68,58;83,69;87,76;74,78;71,71;58,69;54,62;51,67;37,84;41,94;2,99;7,64;22,60;25,62;18,54;4,50;13,40;18,40;24,42;25,38;41,26;45,21;44,35;58,35;62,32;];% C=C(1:10,:); %取前十个城市
N=size(C,1);%TSP问题的规模,即城市数目 (31个),染色体的基因数目
D=zeros(N);%任意两个城市距离间隔矩阵%% 求任意两个城市距离间隔矩阵fori=1:N
forj=1:N
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;endend
NP=200;% 种群数目 染色体条数
G=1000;% 遗传代数
pc=0.8;% 交叉概率
pm=0.5;% 变异概率
f=zeros(NP,N);% 用于存储种群 每一行代表一条染色体
F =[];% 种群更新中间存储fori=1:NP
f(i,:)=randperm(N);% 随机生成初始种群end
best_f =f(1,:);% 存储最优种群
len=zeros(NP,1);% obj:走完所有城市总共要走的路径长度
fitness =zeros(NP,1);% 归一化后的len
gen =0;%% 遗传算法循环
tic;while gen<G
%% 计算路径长度fori=1:NP % 计算所有染色体len(i,1)=D(f(i,N),f(i,1));% 初始化 为城市1到城市终点N的路径长度forj=1:(N-1)len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));% 走完所有城市总共要走的路径长度:(1,N)+(1,2)+(2,3)+....(N-1,N)endend
maxlen =max(len);
minlen =min(len);%% 更新最短路径
rr =find(len==minlen);% 可能有多个相等的min
best_f =f(rr(1,1),:);% 这里取第一个min, best_f代表路径距离len最短的那条路径(怎么个走法)%% 计算归一化适应度fori=1:length(len)% NP fitness=归一化后的路径长度fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));% fitness = - len,即要len越小,fitness则越大end%% 选择操作% % 随机选择% nn = 0;% for i=1:NP % if fitness(i,1)>=rand % rand = 0-1的某个数% nn = nn+1;% F(nn,:)=f(i,:);% end% end% 轮盘赌选择
nn=75;
F=zeros(nn,N);
total_fitness =sum(fitness);
selection_prob = fitness / total_fitness;
cumulative_prob =cumsum(selection_prob);
r =rand(nn,1);% 生成一组随机数fori=1:nn
select=find(cumulative_prob>=r(i));% 下标数组
select_idx=select(1);% 事件序号F(i,:)=f(select_idx,:);end[aa,bb]=size(F);% aa<=NP=200:选出的染色体数目 bb=N=31:染色体基因个数while aa<NP
% 每次循环选出两条染色体
nnper =randperm(nn);% 对数字1-nn随机打乱
A =F(nnper(1),:);
B =F(nnper(2),:);%% 交叉操作if rand<=pc % 交叉概率
W =ceil(N/10);% 交叉点个数
p =unidrnd(N-W+1);% 交叉点范围,随机起始点p,从p到p+Wfori=1:W
x =find(A==B(p+i-1));% 先记录要交换的位置
y =find(B==A(p+i-1));
temp =A(p+i-1);A(p+i-1)=B(p+i-1);B(p+i-1)= temp;
temp =A(x);% 确保所有城市只走一次,即A、B中元素均为1-31,不重复A(x)=B(y);B(y)= temp;endend%% 变异操作if rand<=pm % 变异概率
p1 =floor(1+N*rand());% N*rand()可能<1,因此+1确保>1, floor向下取整
p2 =floor(1+N*rand());while p1==p2 % 确保 p1!=p2
p1 =floor(1+N*rand());
p2 =floor(1+N*rand());end% 逆转变异:计算变异前的路径长度大小
L1_A=D(A(1,1),A(1,N));for k=1:(N-1)
L1_A=L1_A+D(A(1,k),A(1,k+1));end
L1_B=D(B(1,1),B(1,N));for k=1:(N-1)
L1_B=L1_B+D(B(1,k),B(1,k+1));end% 交换位置
tmp =A(p1);A(p1)=A(p2);A(p2)= tmp;
tmp =B(p1);B(p1)=B(p2);B(p2)= tmp;% % 逆转变异:计算变异后的路径长度大小% L2_A=D(A(1,1),A(1,N));% for k=1:(N-1)% L2_A=L2_A+D(A(1,k),A(1,k+1));% end% L2_B=D(B(1,1),B(1,N));% for k=1:(N-1)% L2_B=L2_B+D(B(1,k),B(1,k+1));% end% if L2_A>L1_A % 如果变异后距离变大,则换回来% tmp = A(p1);% A(p1) = A(p2);% A(p2) = tmp;% end% if L2_B>L1_B % 如果变异后距离变大,则换回来% tmp = B(p1);% B(p1) = B(p2);% B(p2) = tmp;% end end
F =[F;A;B];% 添加经过选择、交叉、变异过后的A、B两条染色体[aa,bb]=size(F);endif aa>NP
F =F(1:NP,:);% 保持种群规模为NPend
f = F;% 更新种群f(1,:)= best_f;% 保留每代最优个体
clear F;
gen = gen+1;Rlength(gen)= minlen;end
elapsed_time = toc;%% 绘制图形
figure
fori=1:N-1plot([C(best_f(i),1),C(best_f(i+1),1)],[C(best_f(i),2),C(best_f(i+1),2)],'bo-');text(C(best_f(i),1),C(best_f(i),2),[' 'num2str(best_f(i))])
hold on;endtext(C(best_f(N),1),C(best_f(N),2),[' 'num2str(best_f(N))])plot([C(best_f(N),1),C(best_f(1),1)],[C(best_f(N),2),C(best_f(1),2)],'bo-');title(['优化最短距离:',num2str(minlen)]);
figure
plot(Rlength)xlabel('迭代次数')ylabel('目标函数值')title('适应度进化曲线')fprintf("最短距离: %d\n",min(Rlength()));fprintf("最坏适应度: %d\n",max(Rlength()));fprintf("平均适应度: %d\n",mean(Rlength()));disp(['最短路径:'num2str([best_f best_f(1)])]);disp("程序运行时间为:" + elapsed_time + " 秒");
运行结果
取前10个城市(因为城市较少,很快就试出了全局最小值)
运行结果路径图和适应度进化曲线图
最短距离: 1.665413e+02
最短路径: 2 3 7 8 9 10 5 6 4 1 2
程序运行时间为:0.68586 秒
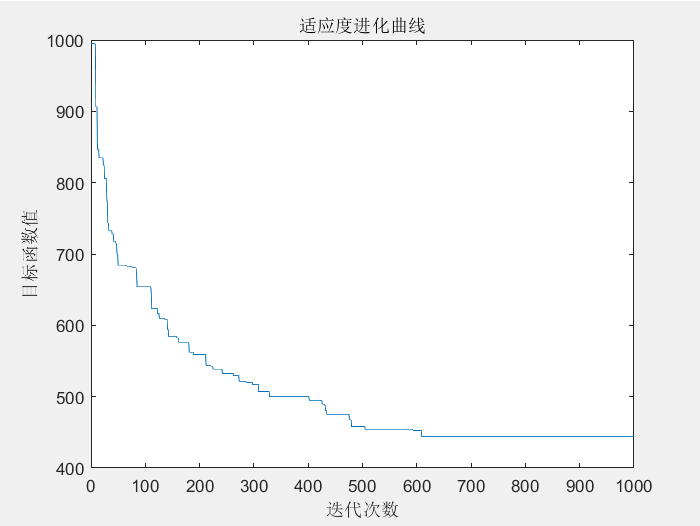
取所有30个城市(参数可能还需要考虑,运行许多遍才得到的较为满意的局部最小值442)
运行结果路径图和适应度进化曲线图
最短距离: 4.638300e+02
最短路径:26 27 29 30 1 2 8 9 7 3 4 6 5 10 11 12 13 14 15 16 17 19 18 20 21 22 23 24 25 28 26
程序运行时间为:1.4892 秒
测试重要参数对结果的影响
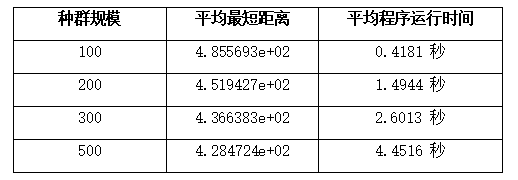
测试种群规模
控制交叉率、变异率不变(0.8、0.5),改变种群规模:
为减少随机性,每个种群规模进行10次实验,计算平均最短距离和平均程序运行时间。
从实验结果来看,种群规模对算法结果和运行时间有一定的影响。随着种群规模的增加,最短距离基本上呈现下降趋势,这是因为较大的种群规模提供了更多的搜索空间,有利于发现更优的解。但同时,随着种群规模继续增加,运行时间也会相应增加。因此实际应用中并不是一直增加种群规模就是好的,还要考虑计算成本。
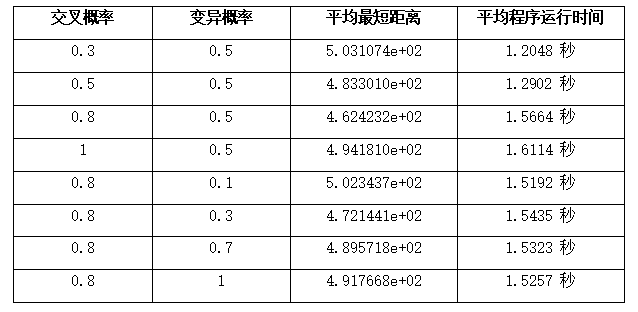
测试交叉率、变异率
同样,也进行10次实验,取平均
交叉概率:
交叉概率对算法结果的影响比较显著。在本实验中,交叉概率为0.8时,获得了最低的最短距离,表明较高的交叉概率有助于保留更好的个体特征。而当交叉概率接近0时,算法结果较差,这是因为没有交叉操作无法引入新的基因组合。另外,当交叉概率过高时,可能会导致过早收敛或陷入局部最优解,导致效果最终搜索到的最优值不佳。而对于运行时间来说,当交叉概率增高时,运行时间明显增加,考虑是轮盘赌选择比较花时间,若交叉概率高,就会进行轮盘赌选择操作,导致计算成本增加。
变异概率:
变异概率对算法结果也有一定的影响。实验结果显示,较低的变异概率可以获得较低的最短距离,表明变异有助于引入新的个体,增加种群的多样性。然而,当变异概率过高时,可能会破坏种群的整体适应度,导致算法性能下降。对于运行时间来说,本实验中设置两点互换变异,变异操作费时较少,因此运行时间几乎不怎么变化。
结果讨论
- 本次实验,不管是对于前10个城市还是所有城市,都可以成功寻得全局最优值,完成了实验的基本要求。 - 对于前10个城市的求解过程中,由于规模较小,基本上一次就能跑出最优结果。 - 对于所有城市的求解过程中,全局最优解往往要通过多次运行代码才能获得,因此对于该遗传算法应该仍有较大的优化空间。
- 遗传算法的核心主要在于:选择、交叉与变异这三个操作,而这三种操作又各有多种方案,如选择方法包含轮盘赌、竞标赛等,变异的话,不止两点交换变异,也可以对某一染色体的基因段进行翻转,还有一种理论上来说更为合理的方案——逆转变异,它在两点变异的基础上,增加了“反悔”的机制,即通过比较变异前后计算得出的适应度值,若变异后适应度变小,则“反悔”这次变异,变回变异之前的模样,这样似乎总能保留下优秀的染色体。但在本实验中效果不佳,不知是代码的编写问题还是其他设置问题,有待考究。
- 选择合适的操作之后,还要对参数进行设置,种群大小、交叉率、变异率,这三个参数可以直接影响是否能够跳出局部最优,寻得全局最优。实验中对它们分别进行了控制变量的实验,虽然该算法本身就具有一定随机性,但多次实验下的结果仍然具有一定参考意义。
🧡🧡蚁群算法求解🧡🧡
主要参数定义
信息素重要程度因子:
这个因子表示了蚂蚁在选择路径时对信息素浓度的重视程度,较大的值意味着蚂蚁更加重视已有路径上的信息素浓度,从而更可能选择已有路径。
启发函数重要程度因子:
启发函数使用了问题特定的信息来评估路径的好坏,本实验中定义启发函数为1/某两个城市的路径长度,这个因子表示了蚂蚁在选择路径时对路径长度的重视程度。
信息素挥发因子:
信息素会随时间挥发,这个因子控制了信息素浓度的挥发速率,较小的值意味着信息素持久性更强,对路径选择的影响更加持久。
进化代数:
蚁群算法迭代的次数,即寻优过程进行的迭代次数。
蚂蚁数量:
在每次迭代中参与搜索的蚂蚁数量,较多的蚂蚁数量可以增加算法的全局搜索能力。
代码
%% 清空环境变量
clear
clc
close all
%% 导入数据% 生成城市坐标
C=[87,7;91,38;83,46;71,44;64,60;68,58;83,69;87,76;74,78;71,71;58,69;54,62;51,67;37,84;41,94;2,99;7,64;22,60;25,62;18,54;4,50;13,40;18,40;24,42;25,38;41,26;45,21;44,35;58,35;62,32;];
C=C(1:30,:);%取前30个城市%% 计算城市间相互距离
citys = C;
n =size(citys,1);
D =zeros(n,n);fori=1:n
forj=1:n
ifi~=jD(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));elseD(i,j)=1e-4;endendend%% 初始化参数rng(39)% 随机因子,确保程序每次运行结果相同
m =45;% 蚂蚁数量
alpha =0.2;% 信息素重要程度因子
beta =7;% 启发函数重要程度因子
rho =0.5;% 信息素挥发因子
iter =1;% 迭代次数初值
iter_max =300;% 最大迭代次数
Q =1;% 常系数
Eta =1./D;% 启发函数
Tau =ones(n,n);% 信息素矩阵
Table =zeros(m,n);% 路径记录表
Route_best =zeros(iter_max,n);% 各代最佳路径
Length_best =zeros(iter_max,1);% 各代最佳路径的长度
Length_ave =zeros(iter_max,1);% 各代路径的平均长度 %% 迭代寻找最佳路径
tic;% 开始计时while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start =zeros(m,1);fori=1:m
temp =randperm(n);start(i)=temp(1);endTable(:,1)= start;% 构建解空间
citys_index =1:n;% 逐个蚂蚁路径选择fori=1:m
% 逐个城市路径选择forj=2:n
tabu =Table(i,1:(j-1));% 已访问的城市集合(禁忌表)
allow_index =~ismember(citys_index,tabu);
allow =citys_index(allow_index);% 待访问的城市集合
P = allow;% 计算城市间转移概率for k =1:length(allow)P(k)=Tau(tabu(end),allow(k))^alpha ...*Eta(tabu(end),allow(k))^beta;end
P = P/sum(P);% 轮盘赌法选择下一个访问城市
Pc =cumsum(P);
target_index =find(Pc >= rand);
target =allow(target_index(1));Table(i,j)= target;endend% 计算各个蚂蚁的路径距离
Length =zeros(m,1);fori=1:m
Route =Table(i,:);forj=1:(n -1)Length(i)=Length(i)+D(Route(j),Route(j+1));endLength(i)=Length(i)+D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter ==1[min_Length,min_index]=min(Length);Length_best(iter)= min_Length;Length_ave(iter)=mean(Length);Route_best(iter,:)=Table(min_index,:);else[min_Length,min_index]=min(Length);Length_best(iter)=min(Length_best(iter -1),min_Length);Length_ave(iter)=mean(Length);ifLength_best(iter)== min_Length
Route_best(iter,:)=Table(min_index,:);elseRoute_best(iter,:)=Route_best((iter-1),:);endend% 更新信息素
Delta_Tau =zeros(n,n);% 逐个蚂蚁计算fori=1:m
% 逐个城市计算forj=1:(n -1)Delta_Tau(Table(i,j),Table(i,j+1))=Delta_Tau(Table(i,j),Table(i,j+1))+ Q/Length(i);% Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/D(j,j+1);% Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q;endDelta_Tau(Table(i,n),Table(i,1))=Delta_Tau(Table(i,n),Table(i,1))+ Q/Length(i);% Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/D(n,1); % Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q; end
Tau =(1-rho)* Tau + Delta_Tau;% 迭代次数加1,清空路径记录表
iter = iter +1;
Table =zeros(m,n);end
elapsedTime = toc;% 结束计时%% 结果显示[Shortest_Length,index]=min(Length_best);
Shortest_Route =Route_best(index,:);disp(['最短距离:'num2str(Shortest_Length)]);disp(['最短路径:'num2str([Shortest_Route Shortest_Route(1)])]);disp(['程序运行时间:',num2str(elapsedTime),'秒']);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
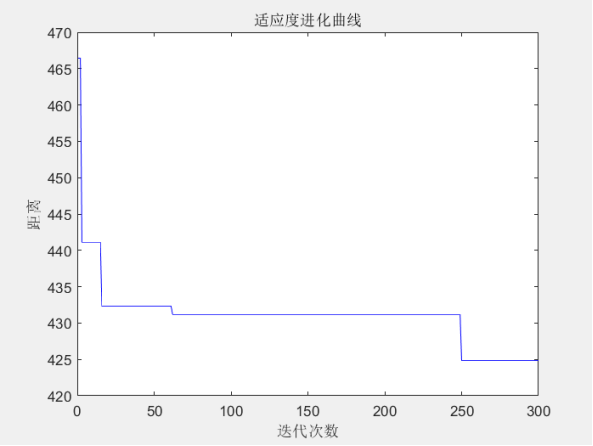
fori=1:size(citys,1)text(citys(i,1),citys(i,2),[' 'num2str(i)]);endxlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:'num2str(Shortest_Length)')'])figure(2)plot(1:iter_max,Length_best,'b')xlabel('迭代次数')ylabel('距离')title('适应度进化曲线')
运行结果
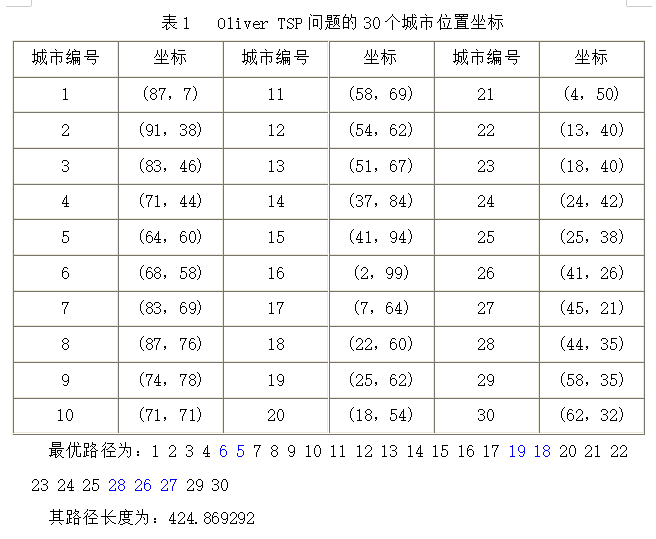
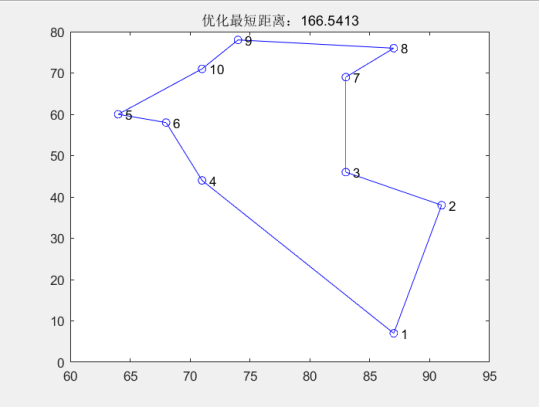
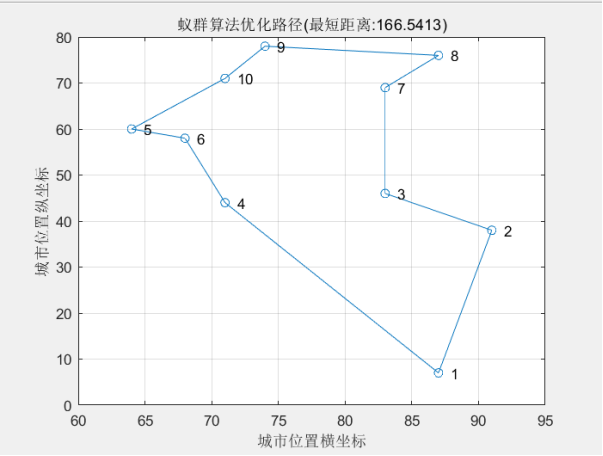
取前10个城市
最短距离:166.5413
最短路径:1 4 6 5 10 9 8 7 3 2 1
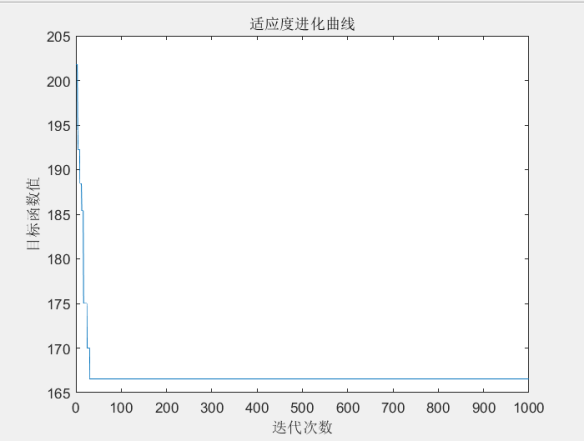
取前30个城市
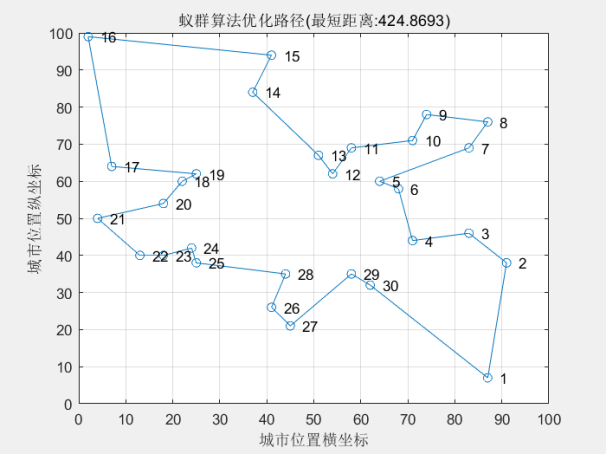
最短距离:424.8693
最短路径:25 24 23 22 21 20 18 19 17 16 15 14 13 12 11 10 9 8 7 5 6 4 3 2 1 30 29 27 26 28 25
测试参数
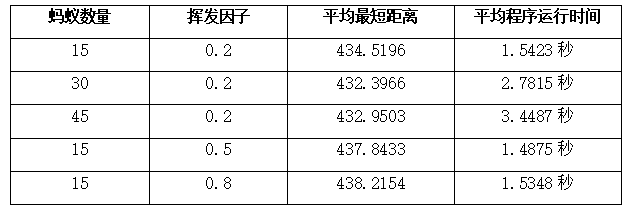
控制信息素重要程度、启发函数重要程度不变,改变蚂蚁数量和挥发因子:
为减少随机性,每个参数进行10次实验,计算平均最短距离和平均程序运行时间。
实验结果表明:
- 蚂蚁数量对算法性能的影响: 蚂蚁数量的增加似乎有助于减小平均最短距离,但同时也会增加程序的运行时间。这表明增加蚂蚁数量可能会提高算法的全局搜索能力,但会增加计算成本。
- 挥发因子对算法性能的影响: 在相同蚂蚁数量的情况下,可以观察到不同挥发因子对平均最短距离和程序运行时间的影响。挥发因子较小时似乎更有利于蚂蚁选择已经存在的路径作为寻优空间。 另外,可以看到最短距离几乎都很接近最优值424,说明大多数参数的其实是搜索空间很相近,不排除测试结果中由于随机因子产生的随机性。 其余参数如信息素重要程度、启发函数重要程度也可以进行同样的测试和比较,这里不再一一赘述。
🧡🧡总结🧡🧡
蚁群算法与遗传算法
区别:
蚁群算法主要是模拟蚂蚁在寻找食物时释放信息素的过程,通过信息素的积累来更新路径,实现优化。
遗传算法主要是利用生物进化的思想,通过种群的选择、交叉、变异等基本操作,不断优化进化得到更好的解。
联系:
蚁群算法和遗传算法都是基于集体智慧的思想,通过群体中个体之间的交互和信息共享来实现全局最优化。
性能对比:
从实验结果来看:
蚁群算法设置好参数后,多次实验结果的求得的最短距离都很小(大多数在430到450之间),而遗传算法尽管同一参数设置好后,多次实验其结果的离散程度比较大,有时能在430,而有时却能在500。究其原因,蚁群算法中启发函数包含了路径长度这个指标,使得每次选择下一个城市时会对城市之间的路径长度具有一定的参照;而遗传算法更注重所有城市长度加起来最小,而没有考虑某两个城市之间的路径是否最优。
从运行时间来看:
蚁群算法只迭代300次,运行时间普遍为2秒以上,而遗传算法迭代1000次,运行时间普遍只需2秒以内,因此,对于TSP问题,蚁群算法相比遗传算法更加耗时。
版权归原作者 在半岛铁盒里 所有, 如有侵权,请联系我们删除。