后缀自动机（SAM）讲解 + Luogu p3804【模板】后缀自动机 (SAM)

SAM

后缀自动机可以存储某一个字符串的所有子串。

一、概念

下图是一个 **字符串

"aababa"

** 的 后缀自动机。

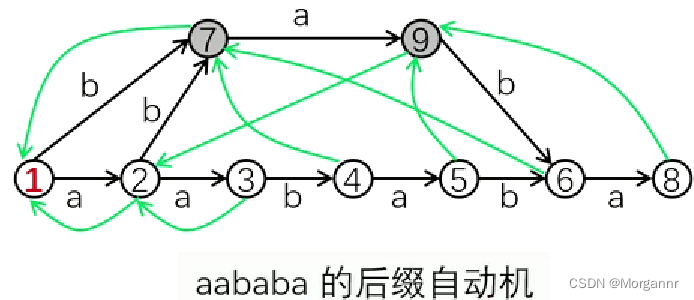
上图中的 黑色边 称 转移边，绿色边 称 链接边。

从根节点沿转移边所走的路径对应一个子串。

根节点表示空串，其他节点 表示 同类子串 的 集合。（同类子串 是指 末尾字母、结束位置相同的子串）

• 解释：上图中，绿色边与节点 构成一棵树（之后再解释），黑色边与节点 构成一张有向无环图，以 6 号点 为例，共有 3 条路径 可以 到达 6 号点，即 6 号点代表 3 个不同的子串（表示 子串的集合）
• 例如 上图中的节点代表集合： ② = { a } ③ = { aa } ④ = { aab } ⑤ = { aaba } ⑥ = { aabab，abab，bab } ⑦ = { ab，b } ⑧ = { aababa，ababa，baba} ⑨ = { aba，ba }
• 发现：同一集合 中的 所有字符串，末尾字母相同，且结束位置相同。（“同类子串集合” 含义），如对于 ⑦ 集合 来说，**endpos("ab") = endpos("b") = { 3，5 }**

二、构建后缀自动机

构建后缀自动机 的过程是一个 动态的过程，也就是 一个一个节点的插入，两类边（转移边，链接边）交替构建。过程中应当 **维护

3

个数组**：

• ch[x][c]：存 节点 x 的 转移边的终点。例：**ch[1][b] = 7, ch[2][b] = 7**（从上图中 ①、② 节点 沿着 b 这条边 能走到 ⑦ 这个 终点）
• fa[x]：存 节点 x 的 链接边的终点。例：**fa[7] = 1，fa[6] = 7**（从上图中 ⑦ 节点 沿着绿边 能走到 ① 这个 终点）
• len[x]：存 节点 x 的 最长串的长度。例：**len[6] = 5，len[7] = 2**（⑥ 号点所代表的字串中 **最长串的长度为 5**）

三、建后缀链接树

构建后缀自动机的目的 并不是在图上进行匹配，而是从图中抽离出 绿色的链接边，构建出一棵树。仔细观察上图，我们发现，每个节点有且只有一条绿色链接边指向其父节点，因此我们可以构造如下图的一棵树，我们称之为 “后缀链接树”：

这棵树有什么 特点？

• 树上节点 表示 同类子串 及其 结束位置 的 集合。（我们将图上的信息完全转移到了这棵树上）

其 合法性：子节点 的 最短串 的 最长后缀 = 父节点 的 最长串，

• 如树中的 ⑥ 号节点 **最短串为 “bab”**，它 **不包括自身的最长后缀是 “ab”**，恰好等于 **其父节点 ⑦ 号节点的 最长串 “ab”**。同样，对于 ⑦ 节点，其 **最短串是 “b”**，它 不包括自身的最长后缀为 空，恰好等于 根节点 ① 的最长串 空。

还可以 发现，从 叶节点往上一直走到根节点 的过程中，字符串的长度 是 递减的，且除了 空 之外，字符串 末尾字母相同，

既然树上存储子串有这些 性质和规律，那我们就可以利用它们来 解决一些问题：

• 节点的子串长度：最长 len[6] = 5，最短 len[6] - len[7] = 3 （对于 最短串长度，我们可以在 遍历的过程中，找出 当前节点 及其 父节点****最长串 长度，二者作差即为当前节点最短串长度）
• 节点的子串数量：**len[6] - len[7] = 3，len[7] - len[1] = 2** （与求当前节点最短串的长度做法一致，将当前节点及其父节点最长串长度作差即可）
• 子串的出现次数：**cnt[4] = 1，cnt[6] = 1，cnt[7] = 2** （上面画的这棵树中，节点旁边的 蓝色数字 代表着 节点代表字符串出现的位置，如 ⑥ 号节点，其代表的所有字符串都 只在 5 位置出现一次，④ 也是如此，而 ④、⑥ 节点的父节点 ⑦ 对应的 “ab”、“b” 两个串 同时 在 3、5 位置出现，也就是对应出现了 两次，而且我们发现 ⑦ 对应的次数 恰好是 其两个儿子 ④、⑥ 次数之和）

四、构建后缀自动机的具体步骤（

extend

函数）

所有步骤 必须 满足上文所说的 “合法性”，这样一来才方便 抽离链接树并进行统计。

我们使用 **变量

tot

为节点进行编号，根节点** 为 **

1

号点，指针

np

** 总是 指向最末创建的节点，也是 从根节点开始（根节点 默认，无需创建）

inttot=1,np=1;

接下来就是 **

3

个数组**，

//fa链接边终点，ch转移边终点，len最长串长度intfa[N],ch[N][26],len[N];

传入 **

extend

函数** 中的 参数 是一个 **偏移量

c

（

0 ~ 25：a ~ z

**，认为 传入的是一个字符）

构建的关键是 **

4

个指针**：

• p：动态回跳指针，**np：固定指向 新点指针，q：固定指向 链接点，nq**：指向 新链接点。

先是 构建 “前奏”：若 **

ch[p][c]

不存在（

p

指向的旧点 沿字符

c

没有可以走到的终点**），就 **从

p

（旧点）向

np

（新点）建 转移边。**

intp=np;np=++tot;//p指向旧点，np是新点len[np]=len[p]+1;cnt[np]=1;//子串出现次数//p沿链接边回跳，从旧点向新点建转移边while(p&&!ch[p][c]){ch[p][c]=np;p=fa[p];}

如果 **退出

for

时

p = 0

**，说明 **

c

是个新字符**，从 新点 向 根节点 建链接边

if(!p)fa[np]=1;//1号为根节点

如果 **退出

for

时

p > 0

**，说明 **

ch[p][c]

存在（

p

指向的旧点 沿字符

c

存在可以走到的终点**），令 **

q = ch[p][c]

**

• (1) 若 p 与 q 的距离 = 1，合法，则 从 np 向 q 建链接边。
• (2) 若 p 与 q 的距离 > 1，不合法，则 裂开 q，从 np 向 nq 建链接边。

else{//如果c是旧字符intq=ch[p][c];//q是链接点//2.若链接点q合法，从新点向q建链接边if(len[q]==len[p]+1)fa[np]=q;//3.若链接点q不合法，则裂开q点，重建两类边else{intnq=++tot;//nq是新链接点，是给新点找到的一个合法的父亲len[nq]=len[p]+1;//重建nq,q,np的链接边fa[nq]=fa[q],fa[q]=fa[np]=nq;//指向q的转移边改为指向nqwhile(p&&ch[p][c]==q){ch[p][c]=nq;p=fa[p];}//从q发出的转移边复制给nqmemcpy(ch[nq],ch[q],sizeofch[q]);}}

分析一下 构建过程中 变量的变化：（红色 标识 初始位置，绿色 标识 回跳后的位置）

• p：动态回跳指针，**np：固定指向 新点指针，q：固定指向 链接点，nq：指向 新链接点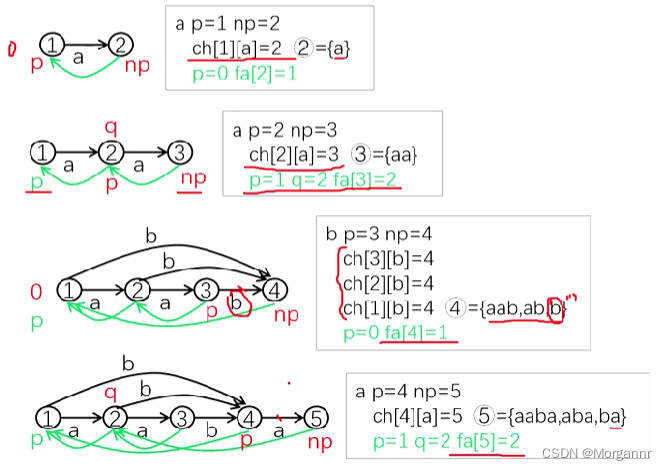 对于上面 插入 4 个字符过程中，链接点 q 都是合法的**，

而对于下方 **插入第

5

个字符

b

时，

p = 5

，

np = 6

**，就出现不合法的情况了，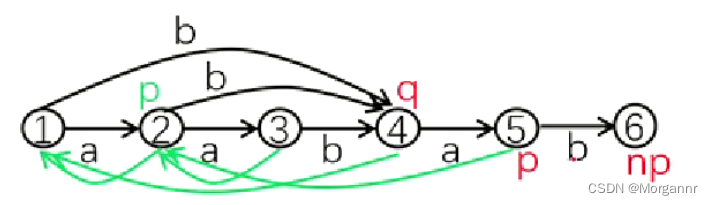
我们首先统计一下 ② ~ ⑥ 号节点所代表的字符串集合：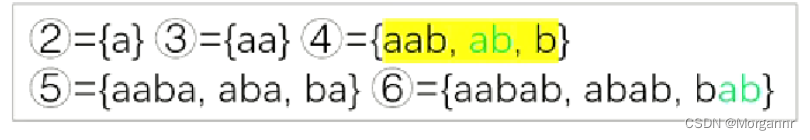
我们将目光放到 ④ 和 ⑥ 节点，对于新点 ⑥，我们应该找 **其集合中的最短串的最长后缀（

"ab"

）**，显然 只有 ④ 节点包含，但是 ④ 节点 并不合法，因为 **其中包含的子串

"ab"

并不是最长的，因此 不满足合法性（无法构造** 后缀 链接树），

怎么办呢？这时候我们就要 将 ④ 号非法链接点裂开，

也就是从这种情况

转变为：

不难发现此时已经 增加了一个合法的链接点 ⑦，接下来就要进行一些 建边操作（共三步，可以与代码相对照理解）

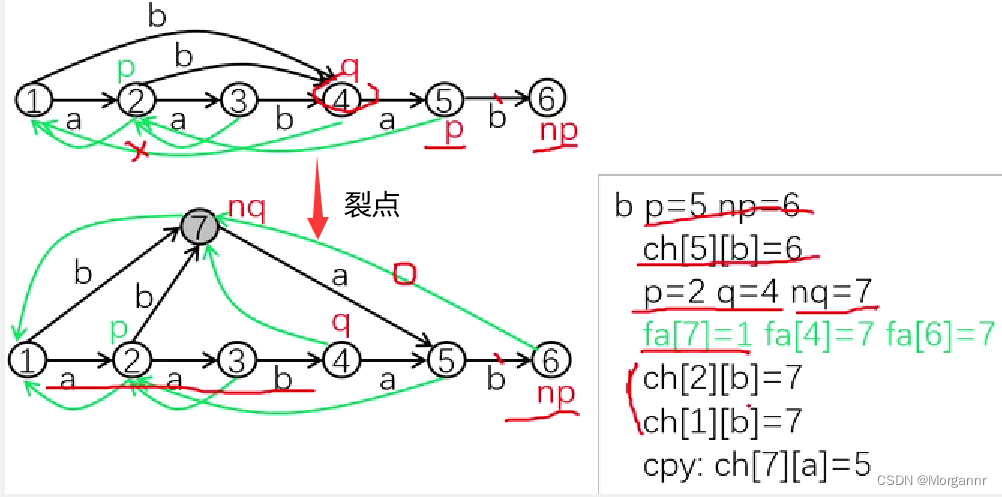
（1）**更改

fa

链接边**，三步走：（观察 裂点前后，两图 边的变化）

• 将 新链接点 nq = 7 指向 q = 4 的父节点：**fa[7] = 1;**
• 将 q = 4 节点 和 新裂开的 nq = 7 节点 链接：**fa[4] = 7;**
• 回到 一开始的目的，给新点找一个 合法链接点：fa[6] = 7;

//重建nq,q,np的链接边fa[nq]=fa[q],fa[q]=fa[np]=nq;

（2）**

for

循环更改

ch

转移边**：由于 ④ 号节点现在只代表 **字符串

"aab"

** 了，因此 原来从 ② 连接到 ④ 和从 ① 连接到 ④ 的边必须要改变指向，具体指向为 新的节点 ⑦。对应上图：**

ch[2][b] = 7, ch[1][b] = 7;

**（观察 裂点前后，两图 边的变化）

//指向q的转移边改为指向nqwhile(p&&ch[p][c]==q){ch[p][c]=nq;p=fa[p];}

（3）创建 从新链接点连出的转移边（有进有出），**复制即可：

cpy：ch[7][a] = 5;

**（观察 裂点前后，两图 边的变化）

//从q发出的转移边复制给nqmemcpy(ch[nq],ch[q],sizeofch[q]);

按照下面的 模型 可以方便理解记忆代码：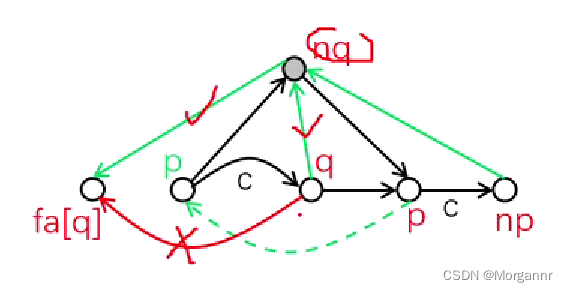

下面 不合法的过程 可在纸上模拟：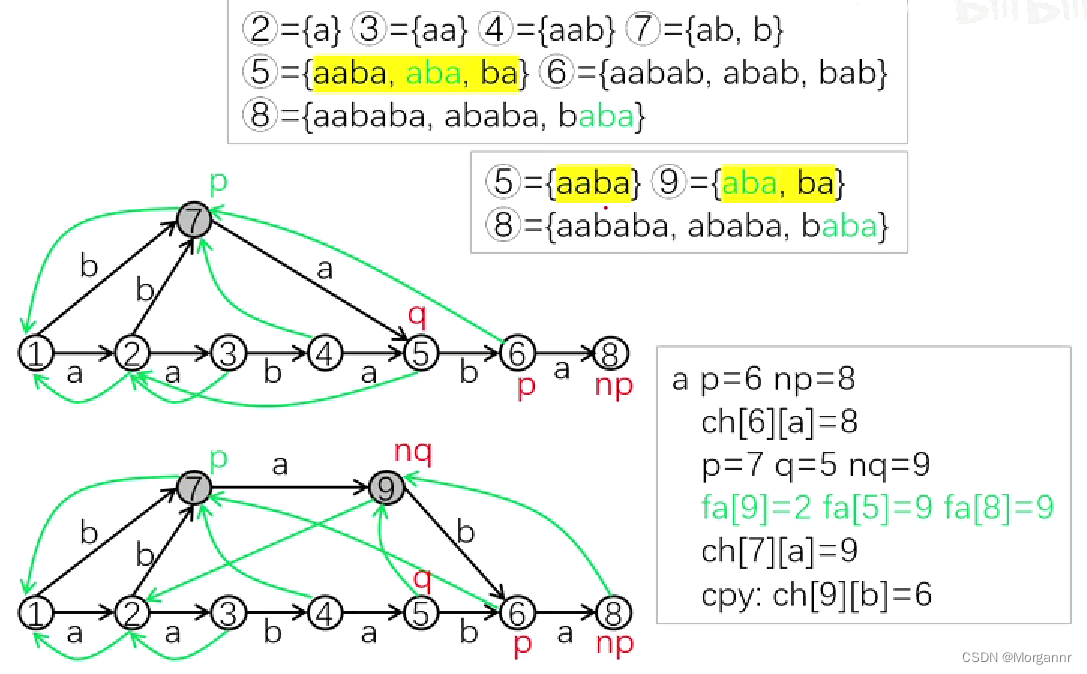

注意：

• 可以证明，长度为 n 的字符串，最多会建 2n - 1 个点和 3n - 4 条边。例如 abb…bb。
• 时间和空间复杂度都是 O(n)
• 建链接树时，点和边都开 2n 的空间
• 节点 7 和 9 是为了 满足子串集合链接的合法性 而创建的，并没影响子串的出现次数，所以 cnt[7，9] = 0

**

SAM

重点：**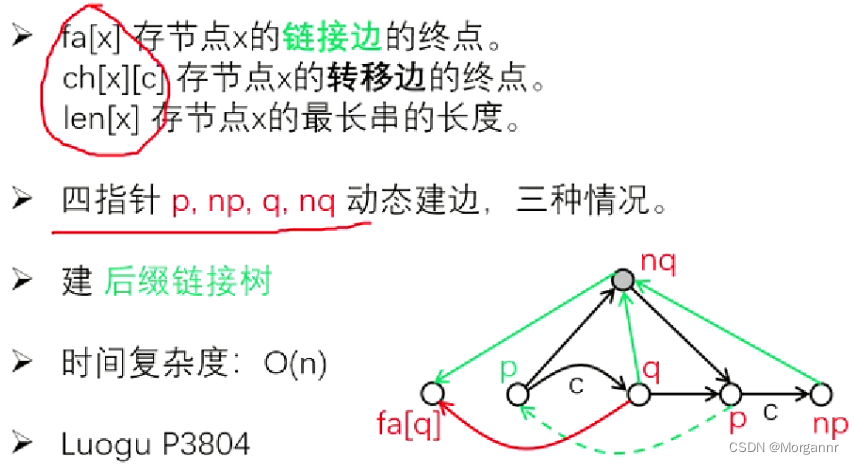

**代码板子：（

extend

函数）**

voidextend(intc){intp=np;np=++tot;len[np]=len[p]+1,cnt[np]=1;while(p&&!ch[p][c]){ch[p][c]=np;p=fa[p];}if(!p){fa[np]=1;}else{intq=ch[p][c];if(len[q]==len[p]+1)fa[np]=q;else{intnq=++tot;len[nq]=len[p]+1;fa[nq]=fa[q],fa[q]=fa[np]=nq;while(p&&ch[p][c]==q){ch[p][c]=nq;p=fa[p];}memcpy(ch[nq],ch[q],sizeofch[q]);}}}

例题【模板】后缀自动机 (SAM)

题目描述

给定一个只包含小写字母的字符串

    S
   
  
  
   S
  
 
S。

请你求出

    S
   
  
  
   S
  
 
S 的所有出现次数不为 

 
  
   
    1
   
  
  
   1
  
 
1 的子串的出现次数乘上该子串长度的最大值。

输入格式

一行一个仅包含小写字母的字符串

    S
   
  
  
   S
  
 
S。

输出格式

一个整数，为所求答案。

样例 #1

样例输入 #1

abab

样例输出 #1

4

提示

对于

    10
   
   
    %
   
  
  
   10 \%
  
 
10% 的数据，

 
  
   
    ∣
   
   
    S
   
   
    ∣
   
   
    ≤
   
   
    1000
   
  
  
   \lvert S \rvert \le 1000
  
 
∣S∣≤1000。

对于

    100
   
   
    %
   
  
  
   100\%
  
 
100% 的数据，

 
  
   
    1
   
   
    ≤
   
   
    ∣
   
   
    S
   
   
    ∣
   
   
    ≤
   
   
    
     10
    
    
     6
    
   
  
  
   1 \le \lvert S \rvert \le {10}^6
  
 
1≤∣S∣≤106。

思路：

构建后缀自动机，之后再后缀链接树上用深度优先遍历进行统计。

代码：（板子）

#include<bits/stdc++.h>usingnamespacestd;//#definemapunordered_map//#defineintlonglongconstintN=1e6+10;typedeflonglongll;chars[N];inttot=1,np=1;intfa[N<<1],ch[N<<1][26],len[N<<1];llcnt[N<<1],ans;vector<int>g[N<<1];voidextend(intc){intp=np;np=++tot;len[np]=len[p]+1,cnt[np]=1;while(p&&!ch[p][c]){ch[p][c]=np;p=fa[p];}if(!p){fa[np]=1;}else{intq=ch[p][c];if(len[q]==len[p]+1)fa[np]=q;else{intnq=++tot;len[nq]=len[p]+1;fa[nq]=fa[q],fa[q]=fa[np]=nq;while(p&&ch[p][c]==q){ch[p][c]=nq;p=fa[p];}memcpy(ch[nq],ch[q],sizeofch[q]);}}}voiddfs(intu){for(autov:g[u]){dfs(v);cnt[u]+=cnt[v];}if(cnt[u]>1)ans=max(ans,cnt[u]*len[u]);}signedmain(){scanf("%s",s);for(inti=0;s[i];++i){extend(s[i]-'a');}for(inti=2;i<=tot;++i){g[fa[i]].push_back(i);}dfs(1);cout<<ans<<'\n';return0;}