前缀树的应用和实现（c++）

前缀树的结构和应用

设有一个仅由字符串组成的数组

string strs[];

我们可以利用前缀树来判断某个字符串是否出现过及其出现次数，还能计算有多少个字符串的前缀是某个前缀

前缀树中，结点不存放数据，数据存储在树的边上，本质是一颗多叉树，最多有26条边来存储26个字符的数据，（本文仅考虑小写字母）。结点需要存放字符经过的次数和有多少字符在这个结点结束

例如，有以下字符串数组

["abc","abe","bce"]

构建方式如下：

从左到右遍历每一个字符串，只要遇到一个字符，就建出一个结点，并在其对应边上存储字符，再把经过次数+1.直到字符串结束，在最后一个字符串中把结束次数+1

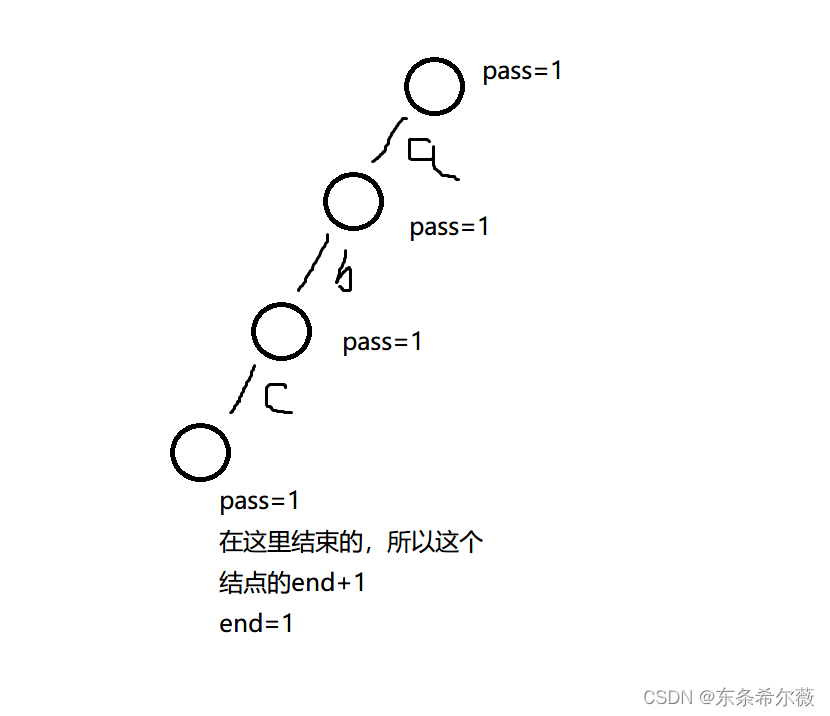
加下一个字符的时候，如果走到了相同的结点，就不用再建新结点，直接把这个结点的pass值+1即可

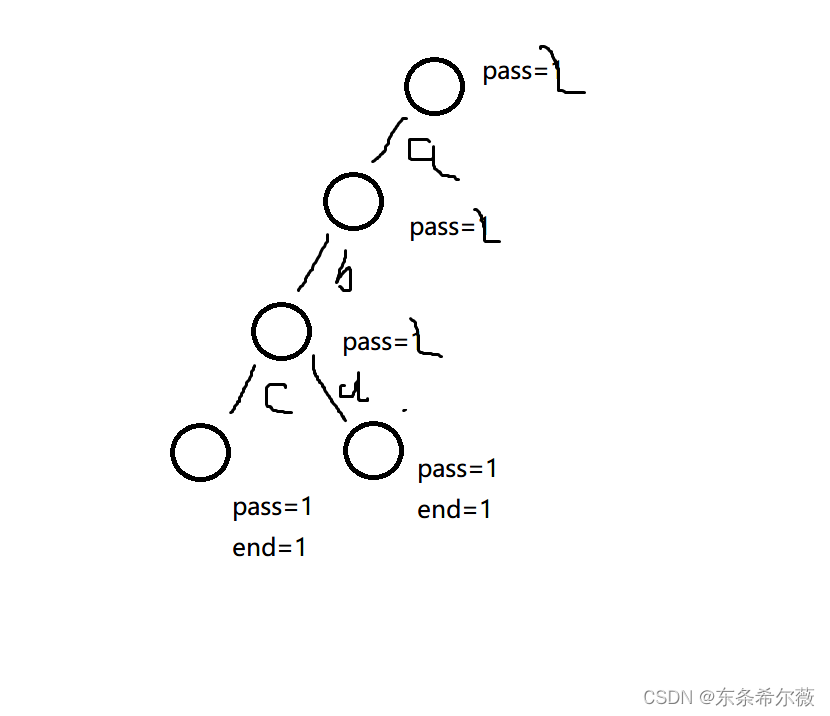
以此类型，就建出了我们的前缀树，注意，这里第一位字符为b，但是不用遍历到b处再建结点，直接在头结点另外建路

前缀树代码实现

前缀树的类定义

我们需要储存每个结点的pass和end值，再准备一个长度为26的指针数组来储存字符信息

至于字符信息怎么表示，我们需要储存的任意字符-'a’就能映射到数组中的对应位置上，例如我们要储存a，那么a-a=0，所以我们就专门在0位置储存字符a，依次类推

classTrieNode{public:int pass;//储存pass值int end;//储存end值
    TrieNode* nexts[26];//在边上储存字符信息TrieNode(){
        pass=0;
        end=0;for(int i=0;i<26;i++){
            nexts[i]=nullptr;}}}

因为我们的前缀树中，包含很多方法，所以我们可以把前缀树的使用再归为一个类，将结点的指针封装起来

classTrieTree{public:TrieTree(){this->root=new TrieNode;}private:
    TrieNode* root;}

前缀树的增加

我们首先当然要遍历某个字符串的每一个字符了

根据前缀树的特点，每个字符的起点都是根结点，所以我们开始就先把根结点的pass++，然后再进行遍历

如果通向某个字符的结点不存在，就直接new一个，如果存在，直接把这个结点的pass值++

voidadd(const string str){if(str,size()==0){return;}
    
    root.pass++;int path=0;//记录字母对应的映射位置
    TrieNode* cur=root;for(int i=0;i<str.size();i++){
        path=str[i]-'a';if(!cur->nexts[path]){
            cur->nexts[path]=new TrieNode;}
        cur=cur->nexts[path];
        cur->pass++;}
    
    cur->end++;}

判断以pre为前缀的字符串有多少个

我们的pass值就派上用场了，pass值忠实的记录了某些字符的经过次数

我们遍历完我们要搜索的字符串，直接返回最后到的结点的pass值即可（表示）

如果中途出现了空结点，就表示字符串数组中的前缀不存在，直接返回即可

intpreNum(string s){if(s.size()==0){return-1;}int path =0;
        TrieNode* cur = root;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(cur->nexts[path]==nullptr){return0;}
            cur = cur->nexts[path];}return cur->pass;}

查找某个字符串在数组中出现了多少次

我们同样遍历我们要搜索的字符串，返回我们最后遍历到的结点的end值即可，（end值就代表这个字符串在这个结点结束了多少次）

intsearchNum(string s){if(s.size()==0){return-1;}

        TrieNode* cur = root;int path =0;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(cur->nexts[path]==nullptr){return0;}
            cur = cur->nexts[path];}return cur->end;}

字符串的删除

我们同样遍历这个字符串，沿途的pass–即可，遍历到最后的字符后，同时end–

但是有一个比较重要的问题：结点的释放问题

当某个结点的pass值已经是0的时候，就代表字符串数组中已经没有这个以及它下面的字符了

怎么释放呢？我们可以考虑用栈释放

每次释放一个点后，再把它的后代压入栈，直到栈为空，表示释放完毕

voiderase(string s){if(s.size()==0||this->searchNum(s)==0){return;}
        TrieNode* cur = root;int path =0;
        cur->pass--;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(--cur->nexts[path]->pass ==0){
                TrieNode* eNode = cur->nexts[path];
                stack<TrieNode*>est;
                est.push(eNode);while(!est.empty()){
                    TrieNode* now = est.top();
                    est.pop();for(int i =0; i <26; i++){if(now->nexts[i]!=nullptr){
                            est.push(now->nexts[i]);}}delete now;}}
            cur = cur->nexts[path];}
        cur->end--;}

完整的前缀树类就如下了

classTrieNode{public:TrieNode(){
        pass =0;
        end =0;for(int i =0; i <26; i++){
            nexts[i]=nullptr;}}int pass;int end;
    TrieNode* nexts[26];};classTrieTree{public:TrieTree(){this->root =new TrieNode;}voidadd(string s){if(s.size()==0){return;}
        TrieNode* cur = root;
        cur->pass++;int path =0;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(cur->nexts[path]==nullptr){
                cur->nexts[path]=new TrieNode;}
            
            
            cur = cur->nexts[path];
            cur->pass++;}
        cur->end++;}intpreNum(string s){if(s.size()==0){return-1;}int path =0;
        TrieNode* cur = root;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(cur->nexts[path]==nullptr){return0;}
            cur = cur->nexts[path];}return cur->pass;}intsearchNum(string s){if(s.size()==0){return-1;}

        TrieNode* cur = root;int path =0;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(cur->nexts[path]==nullptr){return0;}
            cur = cur->nexts[path];}return cur->end;}voiderase(string s){if(s.size()==0||this->searchNum(s)==0){return;}
        TrieNode* cur = root;int path =0;
        cur->pass--;for(int i =0; i < s.size(); i++){
            path = s[i]-'a';if(--cur->nexts[path]->pass ==0){
                TrieNode* eNode = cur->nexts[path];
                stack<TrieNode*>est;
                est.push(eNode);while(!est.empty()){
                    TrieNode* now = est.top();
                    est.pop();for(int i =0; i <26; i++){if(now->nexts[i]!=nullptr){
                            est.push(now->nexts[i]);}}delete now;}}
            cur = cur->nexts[path];}
        cur->end--;}private:
    TrieNode* root;};